求动点速度的问题

我们将从特殊的例题开始，就是考察有重量的质点在真空中（为着不计空气的阻力）的自由降落.

若时间$t$（秒）是从开始降落的时候计算起的，则在这段时间内所经过的路程$s$（米），依已知的公式可表示为

$$s=\dfrac{g}{2} t^2 ,\label{1} \tag{1} $$

式中$g=9.81$（米/秒$^2$）.由此出发，需要确定质点在时刻$t$[即当质点在位置$M$时（图$36$）]的运动的速度$v$.

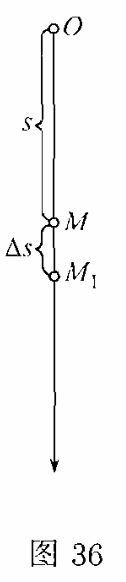
给变量$t$加一增量$\Delta t$，并考察时刻$t+\Delta t$，其时质点在位置$M_1 $.在时间$\Delta t$内的路程的增量$MM_1 $记成$\Delta s$.

在$\eqref{1} $内用$t+\Delta t$代换$t$，则得路程的新值的表达式

$$s+\Delta s=\dfrac{g}{2} (t+\Delta t)^2,$$

由此

$$\Delta s=\dfrac{g}{2} (2t\cdot \Delta t+\Delta t^2).$$

用$\Delta t$除$\Delta s$，我们就得到质点在区间$MM_1 $内降落的平均速度：

$$\overline{v} =\dfrac{\Delta s}{\Delta t} =gt+\dfrac{g}{2} \cdot \Delta t.$$

可见，这速度随着$\Delta t$的变动而变动着，故知在时刻$t$以后所经过的时间$\Delta t$愈少，就愈能更好地表达出质点在时刻$t$的降落情况.

当$\Delta t$趋向于零时质点在时间$\Delta t$内的平均速度$\overline{v} $的极限$v$称为质点在时刻$t$的速度.

在目前的情形，显然

$$v=\lim_{\Delta t\to 0} \left( gt+\dfrac{g}{2} \cdot \Delta t\right) =gt.$$

类似地，可以算出质点在一般直线运动中的速度$v$，质点的位置由它到某一始点$O$的距离$s$所确定；这距离即称为它所经过的路程.时间$t$由某一起始的时刻算起，而且并不一定要从质点在位置$O$的时刻算起.当已经知道运动方程：$s=f(t)$时，运动就作为完全给定的了.质点在任何时刻的位置即可由运动方程确定；在刚才考察的例题内，方程$\eqref{1} $就担任着这种角色.

要确定在所给的时刻$t$的速度$v$，必须同上面那样给$t$以增量$\Delta t$；路程$s$就对应地增大$\Delta s$.比式

$$\dfrac{\Delta s}{\Delta t} $$

表示出在时间$\Delta t$内的平均速度$\overline{v} $.由此，使趋向极限，就得出在时刻$t$的真实速度$v$：

$$v=\lim_{\Delta t\to 0} \overline{v} =\lim_{\Delta t\to 0} \dfrac{\Delta s}{\Delta t} .$$

以下我们将考察另一重要的问题，也将导致相似的极限运算.

在曲线上作切线的问题

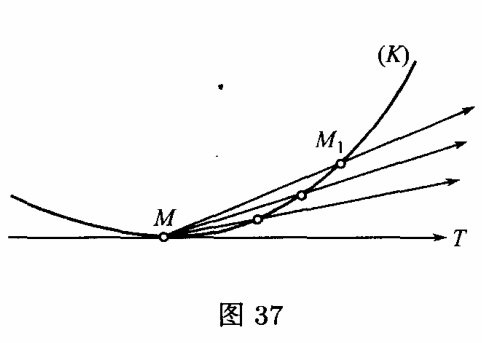
设已给曲线$(K)$及其上一点$M$（图$37$）；今将建立曲线在点$M$处的切线的概念.

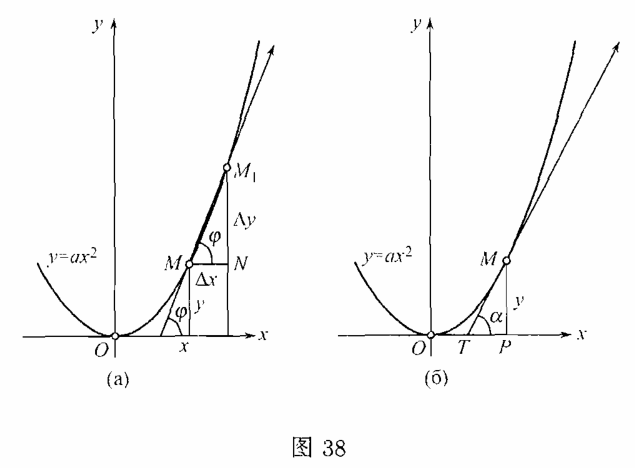
在中学教本内，圆的切线即定义为“与曲线只有一个公共点的直线”.但这定义有特殊性，不能说明相切的本质.例如，若企图应用这定义于抛物线$y=ax^2$（图$38,а$），则在原点$O$处两坐标轴都适合这定义；但在这时大概读者也能立刻明白，事实上仅$x$轴是抛物线在点$O$处的切线！

现在我们就将给出切线的普遍定义.在曲线$(K)$上（图$37$），除点$M$以外再取一点$M_1 $，并引割线$MM_1 $.当点$M_1 $沿曲线移动时，这割线就绕点$M$而转动.

当点$M_1 $沿曲线$(K)$而趋于与$M$重合时，割线$MM_1 $的极限位置$MT$就称为曲线$(K)$在点$M$处的切线（这定义的意义就是，只要弦$MM_1 $充分小，$\angle M_1 MT$就可成为任意小）.

例如，应用这定义求抛物线$y=ax^2$的任意点$M(x,y)$处的切线.因为切线经过这点，那么，要正确地表示它的位置，只要再知道它的斜率就够了.这样，问题就归结于：求在点$M$处切线的斜率$\tan{\alpha } $.

给横标$x$以增量$\Delta x$，即由曲线上的点$M$点移至$M_1 $，这点有横标$x+\Delta x$及纵标

$$y+\Delta y=a\cdot (x+\Delta x)^2$$

（图$38,а$）.割线$MM_1 $的斜率$\tan{\varphi } $由$\triangle MNM_1 $内确定.在这三角形内直角边$MN$等于横标的增量$\Delta x$，而直角边$NM_1 $显然是纵标的对应增量

$$\Delta y=a\cdot (2x\cdot \Delta x+\Delta x^2),$$

于是

$$\tan{\varphi } =\dfrac{\Delta y}{\Delta x} =2ax+a\cdot \Delta x.$$

要得出切线的斜率，很易理解，需要求上式当$\Delta x\to 0$时的极限.这样，我们就得结果

$$\tan{\alpha } =\lim_{\Delta x\to 0} (2ax+a\cdot \Delta x)=2ax.$$

[顺便指出，由此推得抛物线的切线的实际作图的简法.就是$\triangle MPT$（图$38,б$）,线段

$$TP=\dfrac{y}{\tan{\alpha } } =\dfrac{ax^2}{2ax} =\dfrac{x}{2} ,$$

于是$T$是线段$OP$的中点.因此，要作出抛物线在点$M$处的切线，只要平分线段$OP$，把它的中点同$M$连接起来就是.]

在任意曲线的情形，设曲线有方程

$$y=f(x),$$

其切线的斜率可用相似的方法来确定.与横标的增量$\Delta x$对应的纵标的增量是$\Delta y$，比式

$$\dfrac{\Delta y}{\Delta x} $$

表示割线$\tan{\varphi } $.求这比式当$\Delta x\to 0$时的极限，就得出切线的斜率

$$\tan{\alpha } =\lim_{\Delta x\to 0} \tan{\varphi } =\lim_{\Delta x\to 0} \dfrac{\Delta y}{\Delta x} .$$

导数的定义

在解决上面所考察的两个基本问题时，我们所施行的演算，把它们对照起来，就很容易看出，在两种情形内——若抽去变量的意义上的差别——本质上是同一个做法：函数的增量除以自变量的增量，再算出这比式的极限.用这种方法我们就达到微分学的基本概念——导数的概念.

设函数$y=f(x)$是在区间$\mathcal{X} $内定义着的.从自变量的某一数值$x=x_0 $出发，给它加一增量$\Delta x\lessgtr 0$使不越出区间$\mathcal{X} $，于是新值$x_0 +\Delta x$亦属于这区间.那时函数值$y=f(x_0 )$将换成新值$y+\Delta y=f(x_0 +\Delta x)$，即获得增量

$$\Delta y=\Delta f(x_0 )=f(x_0 +\Delta x)-f(x_0 ).$$

若函数的增量$\Delta y$与引起这增量的自变量的增量$\Delta x$的比式当$\Delta x$趋向于$0$时的极限存在，即

$$\lim_{\Delta x\to 0} \dfrac{\Delta y}{\Delta x} =\lim_{\Delta x\to 0} \dfrac{f(x_0 +\Delta x) -f(x_0 )}{\Delta x} $$

存在，这极限就称为函数$y=f(x)$当$x=x_0 $时（或在所给点处$x=x_0 $处）关于自变量$x$的导数.

这样，对于自变量的定值$x=x_0 $，函数的导数——如果存在的话——是一个确定的数；

暂时限于上述极限为有限的情形[参阅[无穷导数]].

若在全区间$\mathcal{X} $内，即对这区间内的每一$x$的数值，导数总存在着，则它仍是$x$的函数.

应用刚才引入的概念，则在[求动点速度的问题]内讲过的动点的速度就可以简括地说成：

速度$v$是动点所经过的路程$s$关于时间$t$的导数.若在更普遍的意义上来理解“速度”这名词，就可以永远把导数当作某一种“速度”来处理.就是，有了自变量$x$的函数$y$，就可以提出变量$y$关于自变量$x$（当已给$x$值时）的变化率（变动的速度）的问题.

若加于$x$的增量$\Delta x$引起$y$的增量$\Delta y$，则仿照[求动点速度的问题]，比式$\dfrac{\Delta y}{\Delta x} $就可以作为当$x$变动一数量$\Delta x$时$y$关于$x$的平均变化率：

$$\overline{V} =\dfrac{\Delta y}{\Delta x} .$$

当$\Delta x$趋向于$0$时这比式的极限自然就称为$y$在所给$x$值时的变化率：

$$V=\lim_{\Delta x\to 0} \overline{V} =\lim_{\Delta x\to 0} \dfrac{\Delta y}{\Delta x} ,$$

即刚好是$y$关于$x$的导数.

在[在曲线上作切线的问题]内我们曾考察由方程$y=f(x)$所给定的曲线，并已解决在给定点处引一切线的问题.现在我们可以把所得的结果叙述为：

切线的斜率$\tan{\alpha } $是纵标$y$关于横标$x$的导数.

导数的这一几何说明经常是有用处的.

我们再补充几个类似于上面已考察过的例子以说明导数的概念.

若运动的速度$v$不是常量，它本身亦随着时间$t$的过程而变动；$v=f(t)$，则称“速度的变化率”为加速度.

就是，若对应于时间的增量$\Delta t$速度的增量为$\Delta v$，则比式

$$\overline{a} =\dfrac{\Delta v}{\Delta t} $$

表示出在时间$\Delta t$内的平均加速度，而它的极限就给出在所给时刻的运动的加速度

$$a=\lim_{\Delta t\to 0} \overline{a} =\lim_{\Delta t\to 0} \dfrac{\Delta v}{\Delta t} .$$

这样，加速度是速度关于时间的导数.

在热学方面，我们将用导数以建立物体以建立在所给温度时的热容量的概念.

用下面的记号表示这问题内引入的物理量：$\theta $是温度（摄氏度），$W$是使物体从$0\, ^{\circ} \mathrm{C} $加热至$\theta \, ^{\circ } \mathrm{C} $所需要的热量（卡）.显然$W$是$\theta $的函数：$W=f(\theta )$.给$\theta $以一增量$\Delta \theta $，则$W$亦得一增量$\Delta W$.物体从$\theta \, ^{\circ } \mathrm{C} $加热至$(\theta +\Delta \theta )\, ^{\circ } \mathrm{C} $时的平均热容量就是

$$\overline{c} =\dfrac{\Delta W}{\Delta \theta } .$$

但一般地说，因为当$\Delta \theta $变动时这平均热容量亦变动着，我们就不能用它作为在所给温度$\theta $时的热容量.要得出后者，必须将上式取极限：

$$c=\lim_{\Delta \theta \to 0} \overline{c} =\lim_{\Delta \theta \to 0} \dfrac{\Delta W}{\Delta \theta } .$$

因此，可以说，物体的热容量是热量关于温度的导数.

最后，从电学内取出一个例子：建立在所给时刻的电流强度的概念.

用$t$表示从某一时刻算起的时间（秒），用$Q$表示在这时间内流过导线的横截面的电量（库仑）.显然$Q$是$t$的函数：$Q=f(t)$.仿照以前的论断，可得在时间$\Delta t$内的平均电流强度是

$$\overline{I} =\dfrac{\Delta Q}{\Delta t} ,$$

而在所给时刻的电流强度则可由极限

$$I=\lim_{\Delta t\to 0} \overline{I} =\lim_{\Delta t\to 0} \dfrac{\Delta Q}{\Delta t} $$

来表示.即电流程度是流过的电量关于时间的导数.

一切这些导数的应用（很容易再多举一些）十分鲜明地表明着一个事实，即导数的概念与各种知识领域内的基本概念是很紧密地关联着的.

导数的求法，其性质的研究及应用就是微分学的主要的研究对象.

导数的表示法常使用各种记号：

$\dfrac{\mathrm{d} y}{\mathrm{d} x} $或$\dfrac{\mathrm{d} f(x_0 )}{\mathrm{d} x} \quad \quad \quad $莱布尼茨($\text{G.W.Leibniz} $)；

我们暂时把莱布尼茨的记法当作整个记号看待；下面[可微性与导数存在之间的关系]我们将看到，它们也可以当作分式看待.

$y’$或$f’(x_0 )\quad \quad \quad \quad $拉格朗日($\text{J.L.Lagrange} $)；

$\mathrm{D} y$或$\mathrm{D} f(x_0 ) \quad \quad \quad $柯西($\text{A.L.Cauchy} $).

以后我们使用拉格朗日的简单的表示法为主.若应用函数表示法$f’(x_0 )$，则在括号内的字母$x_0 $就指在取导数时的那个自变量的数值.最后须指出，有时，当关于哪一个变量而取导数（同它比较以确定“函数的变化率”）都可能发生怀疑时，这变量就用下标的形式写出：

$$y’_x ,f’_x (x_0 ),\mathrm{D}_x y,\mathrm{D}_x f(x_0 ),$$

并且下标$x$与正在取导数的自变量的特殊数值$x_0 $并无关系.

（在某种意义上，可以说，整个记号

$$\dfrac{\mathrm{d} f}{\mathrm{d} x} ,f’或f’_x ,\mathrm{D} f或\mathrm{D}_x f$$

就担任着导函数的函数记号的角色.）

现在应用刚才引入的表示导数的记号，记下前面得出的某些结果.对于运动的速度就有：

$$v=\dfrac{\mathrm{d} s}{\mathrm{d} t} \quad 或\quad v=s’_t ,$$

对于加速度就有：

$$a=\dfrac{\mathrm{d} v}{\mathrm{d} t} \quad 或\quad a=v’_t .$$

类似地，曲线$y=f(x)$的切线的斜率就写成：

$$\tan{\alpha } =\dfrac{\mathrm{d} y}{\mathrm{d} x} \quad 或\quad \tan{\alpha } =y’_x ,$$

以及其他等等.

求导数的例题

现求一系列的初等函数的导数作为例题.

$1^{\circ } \quad $首先注意到明显的结果：若$y=c=$常量，则不论$\Delta x$是怎样的，恒有$\Delta y=0$，于是$y’=0$；又若$y=x$，则$\Delta y=\Delta x$，而$y’=1$.

$2^{\circ } \quad $今设$y=x^n $，此处$n$是自然数.给$x$以增量$\Delta x$；

若所求的是变元的任意值时的导数，则通常就用那表示变元的字母来表示它，而不加任何下标.

则$y$的新的数值就是

$$y+\Delta y=(x+\Delta x)^n=x^n +nx^{n-1} \cdot \Delta x+\dfrac{n(n-1)}{1\cdot 2} x^{n-2} \cdot \Delta x^2 +\cdots .$$

于是

$$\Delta y=nx^{n-1} \cdot \Delta x +\dfrac{n(n-1)}{1\cdot 2} x^{n-2} \cdot \Delta x^2 +\cdots ,$$

而

$$\dfrac{\Delta y}{\Delta x} =nx^{n-1} +\dfrac{n(n-1)}{1\cdot 2} x^{n-2} \cdot \Delta x+\cdots .$$

因为当$\Delta x\to 0$时除首项以外的一切项都趋向于零，故

$$y’=\lim_{\Delta x\to 0} \dfrac{\Delta y}{\Delta x} =nx^{n-1} .$$

$3^{\circ } \quad $若$y=\dfrac{1}{x} $，则$y+\Delta y=\dfrac{1}{x+\Delta x} $，于是

$$\Delta y=\dfrac{1}{x+\Delta x} -\dfrac{1}{x} =\dfrac{-\Delta x}{x(x+\Delta x)} ,$$

而

$$\dfrac{\Delta y}{\Delta x} =-\dfrac{1}{x(x+\Delta x) } .$$

由此

$$y’=\lim_{\Delta x\to 0} \dfrac{\Delta y}{\Delta x} =-\dfrac{1}{x^2} .$$

这时当然假定$x\neq 0$.

$4^{\circ } \quad $考察函数$y=\sqrt{x} (x > 0)$.就有：

$$y+\Delta y=\sqrt{x+\Delta x} ,$$

$$\Delta y=\sqrt{x+\Delta x} -\sqrt{x} =\dfrac{\Delta x}{\sqrt{x+\Delta x} +\sqrt{x} } ,$$

$$\dfrac{\Delta y}{\Delta x} =\dfrac{1}{\sqrt{x+\Delta x} +\sqrt{x} } ;$$

最后，利用根式的连续性，就得

$$y’=\lim_{\Delta x\to 0} \dfrac{\Delta y}{\Delta x} =\dfrac{1}{2\sqrt{x} } .$$

一切这些结果，都可包含在下面的情形内作为它的特殊情形.

$5^{\circ } \quad $幂函数：$y=x^{\mu} $（此处$\mu $是任意实数）.$x$的变动区域依赖于$\mu $；它已在[几类最重要的函数，2°]内被指出.我们有（$x\neq 0$时）

$$\dfrac{\Delta y}{\Delta x} =\dfrac{(x+\Delta x)^{\mu } -x^{\mu } }{\Delta x} =x^{\mu -1} \cdot \dfrac{\left( 1+\dfrac{\Delta x}{x} \right) ^{\mu} -1}{\dfrac{\Delta x}{x} } .$$

若利用[函数的连续性在计算极限时的应用[5）(в)]]内已算出的极限，便有

$$y’=\lim_{\Delta x\to 0} \dfrac{\Delta y}{\Delta x} =\mu x^{\mu -1} .$$

若$\mu > 1$，则很易直接求得在$x=0$时的导数值：$y’=0$.

在特殊情形

若

$$y=\dfrac{1}{x} =x^{-1} ,$$

则$y’=(-1)\cdot x^{-2} =-\dfrac{1}{x^2} ,$

若

$$y=\sqrt{x} =x^{\frac12 } ,$$

则$y’=\dfrac12 x^{-\frac12 } =\dfrac{1}{2\sqrt{x} } .$

$6^{\circ } \quad $指数函数：$y=a^x (a > 0,-\infty < x < +\infty )$.此处

$$\dfrac{\Delta y}{\Delta x} =\dfrac{a^{x+\Delta x} -a^x }{\Delta x} =a^x \cdot \dfrac{a^{\Delta x} -1}{\Delta x} ,$$

利用[函数的连续性在计算极限时的应用[5）(б)]]内已算出的极限，可得：

$$y’=\lim_{\Delta x\to 0} \dfrac{\Delta y}{\Delta x} =a^x \cdot \ln a.$$

特殊情形，

若$y=e^x $，则亦得$y’=e^x $.

因此，指数函数（在$a > 1$时）的增大率与函数值成比例：函数达到愈大的数值时，它在该时刻就增大得愈快.这就表出指数函数增大的准确性质，我们在前面也已经讲到过它了参阅[[无穷大的分阶]].

$7^{\circ } \quad $对数函数：$y=\log_ax (0 < a\neq 1,0 < x < +\infty )$.在这情形

$$\dfrac{\Delta y}{\Delta x} =\dfrac{\log_a (x+\Delta x) -\log_ax }{\Delta x} =\dfrac{1}{x} \cdot \dfrac{\log_a \left( 1+\dfrac{\Delta x}{x} \right) }{\dfrac{\Delta x}{x} } .$$

利用[函数的连续性在计算极限时的应用[5）(а)]]内已算出的极限：

$$y’=\lim_{\Delta x\to 0} \dfrac{\Delta y}{\Delta x} =\dfrac{\log_ae }{x} .$$

特殊情形，对于自然对数就得出非常简单的结果：

在

$$y=\ln x$$

时有$y’=\dfrac{1}{x} .$$

这是作理论研究时宁愿采用自然对数的一种（虽然在本质上并非新的）根据.

对数函数（在$a > 1$时）的增大率与变元的数值成反比，且在变元无限增大时它保持着正值而趋于零，这情况与以前[无穷大的分阶]所讲过的是符合的.

$8^{\circ } \quad $三角函数$\quad $设$y=\sin{x} $，则

$$\dfrac{\Delta y}{\Delta x} =\dfrac{\sin{(x+\Delta x)} -\sin{x} }{\Delta x} =\dfrac{\sin{\dfrac{\Delta x}{2} } }{\dfrac{\Delta x}{2} } \cdot \cos{\left( x+\dfrac{\Delta x}{2} \right) } .$$

利用函数$\cos{x}$的连续性及已知的极限[例题，8）]$\displaystyle \lim_{\alpha \to 0} \dfrac{\sin{\alpha } }{\alpha } =1$，就得

$$y’=\lim_{\Delta x\to 0} \dfrac{\Delta y}{\Delta x} =\cos{x} .$$

注意，这公式的简洁性应归功于用弧度来做角度的单位，假使我们用度数来做角度的单位，则正弦与角的比值的极限将不等于$1$，而很易看出是$\dfrac{\pi }{180} $，那时我们将有

$$(\sin{x} )’=\dfrac{\pi }{180} \cos{x} .$$

类似地，我们可以求：

若$y=\cos{x} $，则$y’=-\sin{x} $.

在$y=\tan{x} $时，有

$$\begin{align}
\dfrac{\Delta y}{\Delta x} & =\dfrac{\tan{(x+\Delta x)} -\tan{x} }{\Delta x} \\
& =\dfrac{\dfrac{\sin{(x+\Delta x)} }{\cos{(x+\Delta x)} } -\dfrac{\sin{x} }{\cos{x} } }{\Delta x} \\
& =\dfrac{\sin{(x+\Delta x)} \cdot \cos{x} -\cos{(x+\Delta x)} \cdot \sin{x} }{\Delta x \cdot \cos{x} \cdot \cos{(x+\Delta x)} } \\
& =\dfrac{\sin{\Delta x} }{\Delta x} \cdot \dfrac{1}{\cos{x} \cdot \cos{(x+\Delta x)} } .\\
\end{align}$$

由此，同上面一样，

$$y’=\lim_{\Delta x\to 0} \dfrac{\Delta y}{\Delta x} =\dfrac{1}{\cos{} ^2 x} =\sec{} ^2 x.$$

类似地，

若$y=\cot{x} $，则$y’=-\dfrac{1}{\sin{} ^2 x} =-\csc{} ^2 x.$

反函数的导数

在求反三角函数的导数之前，先证明下面的普遍的定理.

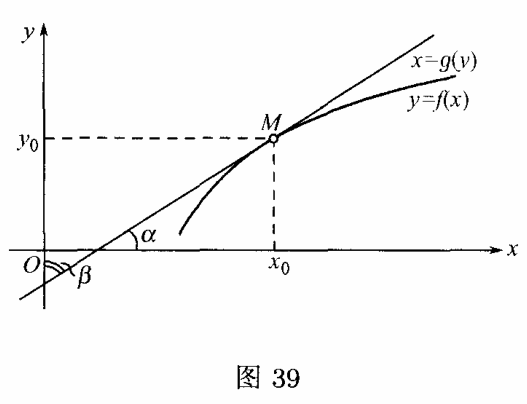
定理$\quad $设$1)$函数$f(x)$满足[反函数的存在]中关于反函数存在的定理的条件，$2)$在点$x_0$有异于零的有限导数$f’(x_0 )$.于是在对应点$y_0 =f(x_0 )$反函数$g(y)$的导数$g’(y_0 )$也存在，且等于$\dfrac{1}{f’(x_0 )}$.

证明$\quad $给数值$y=y_0 $以任意的增量$\Delta y$，则函数$x=g(y)$亦将获得对应的增量$\Delta x$.注意，在$\Delta y\neq 0$时，由于函数$y=f(x)$的单值性，亦必有$\Delta x\neq 0$.就有

$$\dfrac{\Delta x}{\Delta y} =\dfrac{1}{\dfrac{\Delta y}{\Delta x} } .$$

今若（依任意规律）使$\Delta y\to 0$，则——由于假定函数$x=g(y)$是连续的——增量$\Delta x\to 0$.但那时上式右端的分母趋于极限$f’(x_0 )\neq 0$，因此，左端的极限存在，且等于其倒数$\dfrac{1}{f’(x_0 )} $；它就是导数$g’(y_0 )$.

因此，就有简单的公式：

$$x’_y =\dfrac{1}{y’_x} .$$

很易说明它的几何意义.我们知道，导数$y’_x $是函数$y=f(x)$的图像上的切线与$x$轴间的角$\alpha $的正切.但反函数$x=g(y)$有着同一的图像，不过它的自变量是$y$罢了.因此导数$x’_y $等于同一切线与$y$轴间的角$\beta $的正切（图$39$）.这样，上面导出的公式就变成大家知道的关系式

$$\tan{\beta } =\dfrac{1}{\tan{\alpha } } ,$$

其中$\alpha $与$\beta $之和等于$\dfrac{\pi }{2} $.

令$y=a^x $作为例子.它的反函数就是$x=\log_ay $.因为（参阅$6^{\circ }$）$y’_x =a^x \cdot \ln a$，故依目前的公式，有

$$x’_y =\dfrac{1}{y’_x } =\dfrac{1}{a^x \cdot \ln a} =\dfrac{\log_ae }{y} ,$$

与$7^{\circ }$相符合.

现在要转到求反三角函数的导数，为了方便，我们把变量$x$与$y$互相对调，把已证明的公式改写成

$$y’_x =\dfrac{1}{x’_y } .$$

$9^{\circ } \quad $反三角函数$\quad $考察函数$y=\arcsin{x} (-1 < x < 1)$，其中$-\dfrac{\pi}{2} < y < \dfrac{\pi }{2} $.它是$x=\sin{y} $的反函数.函数$x=\sin{y} $当$y$在刚才指定的范围内时有正值的导数$x’_y =\cos{y} $，在这种情形导数$y’_x $也存在，且依我们的公式

$$y’_x =\dfrac{1}{x’_y } =\dfrac{1}{\cos{y} } =\dfrac{1}{\sqrt{1-\sin{} ^2 y} } =\dfrac{1}{\sqrt{1-x^2} } ;$$

因$\cos{y} > 0$，根式前应取正号.

我们除去$x=\pm 1$的数值，因为与它对应的数值是$y=\pm \dfrac{\pi }{2} $，在这时导数$x’_y =\cos{y} =0$.

函数$y=\arctan{x} (-\infty < x < +\infty )$是函数$x=\tan{y} $的反函数.依我们的公式

$$y’_x =\dfrac{1}{x’_y } =\dfrac{1}{\sec{} ^2 y} =\dfrac{1}{1+\tan{} ^2 y} =\dfrac{1}{1+x^2} .$$

类似地可以得出

对于

$$y=\arccos{x} ,y’=-\dfrac{1}{\sqrt{1-x^2} } \quad (-1 < x < 1),$$

对于

$$y=\text{arccot} \;x ,y’=-\dfrac{1}{1+x^2} \quad (-\infty < x < \infty ).$$

导数公式一览表

现在把我们已求出的一切导数公式列成一览表如下：

$$\begin{array}{lll}
1 . & \quad y=c & \quad y’=0 \\
2 . & \quad y=x & \quad y’=1 \\
3 . & \quad y=x^{\mu} & \quad y’=\mu x^{\mu -1} \\
& \quad y=\dfrac{1}{x} & \quad y’=-\dfrac{1}{x^2} \\
& \quad y=\sqrt{x} & \quad y’=\dfrac{1}{2\sqrt{x} } \\
4 . & \quad y=a^x & \quad y’=a^x \cdot \ln a \\
& \quad y=e^x & \quad y’=e^x \\
5 . & \quad y=\log_ax & \quad y’=\dfrac{\log_ae }{x} \\
& \quad y=\ln x & \quad y’=\dfrac{1}{x} \\
6 . & \quad y=\sin{x} & \quad y’=\cos{x} \\
7 . & \quad y=\cos{x} & \quad y’=-\sin{x} \\
8 . & \quad y=\tan{x} & \quad y’=\sec{} ^2 x =\dfrac{1}{\cos{} ^2 x} \\
9 . & \quad y=\cot{x} & \quad y’=-\csc{} ^2 x =-\dfrac{1}{\sin{} ^2 x} \\
10 . & \quad y=\arcsin{x} & \quad y’=\dfrac{1}{\sqrt{1-x^2} } \\
11 . & \quad y=\arccos{x} & \quad y’=-\dfrac{1}{\sqrt{1-x^2} } \\
12 . & \quad y=\arctan{x} & \quad y’=\dfrac{1}{1+x^2 } \\
13 . & \quad y=\text{arccot} \;x & \quad y’=-\dfrac{1}{1+x^2 } \\
\end{array}$$

函数的增量的公式

先在这里证明两个简单的命题，它们在以后是有用的.

设函数$y=f(x)$是在区间$\mathcal{X} $内定义着的.从这区间内的一个固定值$x=x_0 $出发，用$\Delta x\gtrless 0$表示$x$的任意增量，但须限制$x_0 +\Delta x$使不越出$\mathcal{X} $的范围以外.于是对应的函数的增量就是

$$\Delta y=\Delta f(x_0 ) =f(x_0 +\Delta x) -f(x_0 ).$$

$1^{\circ} \quad $若函数$y=f(x)$在点$x_0 $处有（有限的）导数$y’_x =f’(x_0 )$，则函数的增量可以表示为如下的形式：

$$\Delta f(x_0 ) =f’(x_0 )\cdot \Delta x+\alpha \cdot \Delta x\label{2} \tag{2} $$

或更简短地

$$\Delta y=y’_x \cdot \Delta x+\alpha \cdot \Delta x,\label{21} \tag{2a} $$

式中的$\alpha $是依赖于$\Delta x$的量，且随着$\Delta x$一同趋于零.

因为由导数的定义，在$\Delta x\to 0$时

$$\dfrac{\Delta y}{\Delta x} \to y’_x ,$$

故令

$$\alpha =\dfrac{\Delta y}{\Delta x} -y’_x ,$$

就看出也有$\alpha \to 0$.由此解出$\Delta y$，即得公式$\eqref{21} $.

因为量$\alpha \cdot \Delta x$（在$\Delta x\to 0$时）是较$\Delta x$更高阶的无穷小，故使用在[无穷小的比较]内引入的记法，我们的公式就可以改写成

$$\Delta f(x_0 ) =f’(x_0 )\cdot \Delta x+o(\Delta x) \label{3} \tag{3} $$

或

$$\Delta y=y’_x \cdot \Delta x+o(\Delta x).\label{31} \tag{3a} $$

附注$\quad $到现在为止，我们算作$\Delta x\gtrless 0$；故量$\alpha $在$\Delta x=0$时是不曾定义的.当我们说在$\Delta x\to 0$时$\alpha \to 0$，必已预先假设（像通常那样）$\Delta x$系依任意规律趋于零，但并不取得零值.现在就令在$\Delta x=0$时$\alpha =0$；那时公式$\eqref{2} $在$\Delta x=0$时自然仍为有效.然除此以外，$\Delta x\to 0$时$\alpha \to 0$这一关系却可比以前得到更广义的理解，就是在$\Delta x$趋于零的过程中，它也可以取等于零的数值了.

由已证明的公式直接推得：

$2^{\circ} \quad $若函数$y=f(x)$在点$x_0 $处有（有限的）导数，则函数在这点必然是连续的.

实因，由$\eqref{21} $，很清楚地，由$\Delta x\to 0$的关系就立即引出$\Delta y\to 0$.

求导数的几个简单法则

在前几目内我们已求出初等函数的导数.在这一目及下面一目内，我们将建立一系列的法则，用了它们就可以求任何由初等函数经过有限次的算术运算及叠置[函数的叠置.总结]所得出的函数的导数.

Ⅰ.设函数$u=\varphi (x)$（在定点$x$处）有导数$u’$.我们要证明，函数$y=cu$（$c=$常数）（在同一点处）也有导数，并求出它.

若自变量$x$得一增量$\Delta x$，则函数$u$亦得一增量$\Delta u$，而由开始的数值$u$变为数值$u+\Delta u$.函数$y$的新值就是$y+\Delta y=c(u+\Delta u)$.

由此$\Delta y=c\cdot \Delta u$而

$$\lim_{\Delta x\to 0} \dfrac{\Delta y}{\Delta x} =c\cdot \lim_{\Delta x\to 0} \dfrac{\Delta u}{\Delta x} =c\cdot u’.$$

因此，导数存在且等于

$$y’=(c\cdot u)’=c\cdot u’.$$

这公式表示这样一条法则：常数因子可以从导数的符号内取出.

Ⅱ.设函数$u=\varphi (x),v=\phi (x)$，（在定点$x$处）有导数$u’,v’$.今证明，函数$y=u\pm v$（在同一点处）也有导数，并求出它.

给$x$以增量$\Delta x$；于是$u,v$及$y$就对应地各得增量$\Delta u ,\Delta v$及$\Delta y$.它们的新值$u+\Delta u$，$v+\Delta v$及$y+\Delta y$可用同样的关系式连接着：

$$y+\Delta y=(u+\Delta u)\pm (v+\Delta v),$$

由此

$$\Delta y=\Delta u\pm \Delta v,\dfrac{\Delta y}{\Delta x} =\dfrac{\Delta u}{\Delta x} \pm \dfrac{\Delta v}{\Delta x} $$

而

$$\lim_{\Delta x\to 0} \dfrac{\Delta y}{\Delta x} =\lim_{\Delta x\to 0} \dfrac{\Delta u}{\Delta x} \pm \lim_{\Delta x\to 0} \dfrac{\Delta v}{\Delta x} =u’\pm v’,$$

于是导数$y’$存在且等于

$$y’=(u\pm v)’=u’\pm v’.$$

这结果可以很容易地推广到任意有限个加数的情形（用同样的方法）.

Ⅲ.在关于函数$u,v$的同样的假定下，我们证明，函数$y=u\cdot v$也有导数，并求出它.

同上面一样，对应于增量$\Delta x$有增量$\Delta u,\Delta v$及$\Delta y$；这时$y+\Delta y=(u+\Delta u)(v+\Delta v)$，于是

$$\Delta y=\Delta u\cdot v+u\cdot \Delta v+\Delta u\cdot \Delta v$$

及

$$\dfrac{\Delta y}{\Delta x} =\dfrac{\Delta u}{\Delta x} \cdot v+u\cdot \dfrac{\Delta v}{\Delta x} +\dfrac{\Delta u}{\Delta x} \cdot \Delta v.$$

因为根据[函数的增量的公式，$2^{\circ }$]，当$\Delta x\to 0$也有$\Delta v\to 0$，故

$$\lim_{\Delta x\to 0} \dfrac{\Delta y}{\Delta x} =\lim_{\Delta x\to 0} \dfrac{\Delta u}{\Delta x} \cdot v +u \cdot \lim_{\Delta x\to 0} \dfrac{\Delta v}{\Delta x} =u’\cdot v+u\cdot v’,$$

即导数$y’$存在并等于

$$y’=(u\cdot v)’=u’\cdot v+u\cdot v’.$$

若$y=uvw$，并且$u’,v’,w’$都存在，则

$$y’=[(uv)\cdot w]’=(uv)’\cdot w+(uv)\cdot w’=u’vw+uv’w+uvw’.$$

很易判断，在$n$个因子相乘时将类似地有：

$$[\overbrace{uvw\cdots s}^{n} ]’=u’vw\cdots s+uv’w\cdots s+uvw’\cdots s+\cdots +uvw\cdots s’.\label{4} \tag{4} $$

要证明这事，我们利用数学归纳法.假定公式$\eqref{4} $在$n$个因子相乘时是真实的，再证明它在$(n+1)$个因子相乘时也是真实的：

$$[\overbrace{uvw\cdots st}^{n+1} ]’=[\overbrace{uvw\cdots s}^{n} \cdot t]’=(uvw\cdots s)’\cdot t+(uvw\cdots s)\cdot t’;$$

将导数$(uvw\cdots s)’$依公式$\eqref{4} $展开，就得出公式

$$[uvw\cdots st]’=u’vw\cdots st+uv’w\cdots st+\cdots +uvw\cdots s’t+uvw\cdots st’,$$

完全类似于$\eqref{4} $.因为公式$\eqref{4} $在$n=2$及$3$时的真实性我们已直接证明了，所以这公式对于任意的$n$也是真实的.

Ⅳ.最后，若$u,v$满足于前面的假定，此外，又假定$v$异于零，则我们将证明，函数$y=\dfrac{u}{v} $也有导数，并求出它.

用上面一样的表示法，就有

$$y+\Delta y=\dfrac{u+\Delta u}{v+\Delta v} ,$$

于是

$$\Delta y=\dfrac{\Delta u\cdot v-u\cdot \Delta v}{v(v+\Delta v)} ,$$

而

$$\dfrac{\Delta y}{\Delta x} =\dfrac{\dfrac{\Delta u}{\Delta x} \cdot v-u\cdot \dfrac{\Delta v}{\Delta x} }{v\cdot (v+\Delta v)} .$$

在此处使$\Delta x$趋向于零（则同时亦有$\Delta v\to 0$），就证明了导数的存在，且

$$y’=\left( \dfrac{u}{v} \right)’=\dfrac{u’\cdot v-u\cdot v’}{v^2} .$$

复合函数的导数

现在我们可以建立一条在实际求导数时十分重要的法则.只要被组合的各个函数的导数已经知道时，我们就能够按法则来求复合函数的导数.

Ⅴ.设$1)$函数$u=\varphi (x)$在某一点$x_0 $处有导数$u’_x =\varphi’(x_0 )$，$2)$函数$y=f(u)$在对应点$u_0 =\varphi (x_0 )$也有导数$y’_u =f’(u)$.于是复合函数$y=f(\varphi (x))$在上述的点$x_0 $处亦将有导数，它等于$f(u)$的导数与$\varphi(x) $的导数的乘积：

$$[f(\varphi (x_0 ))]’ =f’_u (\varphi (x_0 )) \cdot \varphi’(x_0 ),$$

须着重指出，记号$f’_u (\varphi (x_0 ))$表示函数$f(u)$关于变元$u$（并非关于$x$）的导数在这个变元取值$u_0 =\varphi (x_0 )$时的值.

或更简短地

$$y’_x =y’_u \cdot u’_x .$$

为了证明，给$x$以任意增量$\Delta x$；设$\Delta u$是函数$u=\varphi (x)$的对应增量，又最后，$\Delta y$是增量$\Delta u$所引起的函数$y=f(u)$的增量.利用关系式$\eqref{21} $，把$x$换成$u$，就改写成

$$\Delta y=y’_u \cdot \Delta u+\alpha \cdot \Delta u$$

（$\alpha $依赖于$\Delta u$并与它一同趋向于零）.用$\Delta x$除各项，就得

$$\dfrac{\Delta y}{\Delta x} =y’_u \cdot \dfrac{\Delta u}{\Delta x} +\alpha \cdot \dfrac{\Delta u}{\Delta x} .$$

若$\Delta x$趋于零，则$\Delta u$亦趋向于零[函数的增量的公式，$2^{\circ }$]，于是，我们知道，依赖于$\Delta u$的量$\alpha $亦将趋于零.因此，有极限存在

$$\lim_{\Delta x\to 0} \dfrac{\Delta y}{\Delta x} =y’_u \cdot \lim_{\Delta x\to 0} \dfrac{\Delta u}{\Delta x} =y’_u \cdot u’_x ,$$

它就是所求的导数$y’_x $.

附注$\quad $在此处就表现了[函数的增量的公式]中的附注的用处了：当$\Delta x$是自变量的增量时，我们可以假定它异于零，但对于$x$的函数$u=\varphi (x)$的增量$\Delta u$来说，即使在$\Delta x\neq 0$时我们也没有权利设想$\Delta u\neq 0$了.

例题

以下用字母$x,y,u,v$表示变量，而别的字母就表示常量.

先举几个应用法则Ⅰ~Ⅳ的例题.

$1)$考察多项式：

$$y=a_0 x^n +a_1 x^{n-1} +\cdots +a_{n-2} x^2 +a_{n-1} x+a_n .$$

先依法则Ⅱ，再依法则Ⅰ，就有

$$\begin{align}
y’ & = (a_0 x^n )’+(a_1 x^{n-1} )’+\cdots +(a_{n-2} x^2 )’+(a_{n-1} x)’+(a_n )’ \\
& =a_0 (x^n)’ +a_1 (x^{n-1})’ +\cdots +a_{n-2} (x^2)’+a_{n-1} (x)’+(a_n )’ .
\end{align}$$

利用[导数公式一览表]公式$1,2,3$，最后得

$$y’=na_0 x^{n-1} +(n-1)a_1 x^{n-2} +\cdots +2a_{n-2} x+a_{n-1} .$$

$2)\;y=(2x^2-5x+1)\cdot e^x$.依法则Ⅲ

$$y’=(2x^2-5x+1)’\cdot e^x +(2x^2-5x+1)\cdot (e^x)’ .$$

根据前一例题及[导数公式一览表]公式$4$，求出

$$y’=(4x-5)\cdot e^x +(2x^2-5x+1)\cdot e^x =(2x^2-x-4)\cdot e^x .$$

$3)\;y=\dfrac{ax+b}{x^2+1} $.依法则Ⅳ，

$$\begin{align}
y’ & = \dfrac{(ax+b)’(x^2+1)-(ax+b)(x^2+1)’}{(x^2+1)^2} \\
& =\dfrac{a(x^2+1)-(ax+b)\cdot 2x}{(x^2+1)^2} \\
& =\dfrac{-ax^2-2bx+a}{(x^2+1)^2} .\\
\end{align}$$

$4)$再求函数$y=\tan{x} $的导数，从公式$y=\dfrac{\sin{x} }{\cos{x} } $出发.应用法则Ⅳ（及[导数公式一览表]的公式$6,7$）得

$$\begin{align}
y’ & = \dfrac{(\sin{x} )’\cdot \cos{x} -\sin{x} \cdot (\cos{x} )’}{\cos{} ^2 x} \\
& =\dfrac{\cos{} ^2 x+\sin{} ^2 x}{\cos{} ^2 x} \\
& =\dfrac{1}{\cos{} ^2 x} \\
\end{align}$$

（参阅[导数公式一览表]，$8$）.

$5)\;y=\dfrac{x\sin{x} +\cos{x} }{x\cos{x} -\sin{x} } $.在这里必须先应用法则Ⅳ，再应用法则Ⅱ及Ⅲ（及[导数公式一览表]公式$6,7$）:

$$\begin{align}
y’ & = \dfrac{(x\sin{x} +\cos{x} )’(x\cos{x} -\sin{x} ) -(x\sin{x} +\cos{x} )(x\cos{x} -\sin{x} )’}{(x\cos{x} -\sin{x} )^2} \\
& = \dfrac{x\cos{x} \cdot (x\cos{x} -\sin{x} ) -(x\sin{x} +\cos{x} )\cdot (-x\sin{x} )}{(x\cos{x} -\sin{x} )^2} \\
& = \dfrac{x^2}{(x\cos{x} -\sin{x} )^2} .\\
\end{align}$$

这里分子与分母的导数是立刻算出的，并未分开为两个步骤.通过习题必须达到一般地能立刻写出导数的地步.

求复合函数的导数的例题：

$6)$设$y=\ln \sin{x} $，换言之，$y=\ln u$，$u=\sin{x} $.依法则Ⅴ，$y’_x =y’_u \cdot u’_x $.导数$y’_u =(\ln u)’_u =\dfrac{1}{u} $（公式$5$）应当对$u=\sin{x} $来取.这样

$$y’_x =\dfrac{1}{\sin{x} } \cdot (\sin{x} )’=\dfrac{\cos{x} }{\sin{x} } =\cot{x} .\tag{公式6} $$

$7)\;y=\sqrt{1+x^2} $，即$y=\sqrt{u} $，式中$u=1+x^2 $；依法则Ⅴ，

$$y’_x =\dfrac{1}{2\sqrt{1+x^2} } \cdot (1+x^2)’=\dfrac{x}{\sqrt{1+x^2} } .\tag{公式3,例1} $$

$8)\;y=e^{x^2} $，即$y=e^u $，式中$u=x^2$；

$$y’_x =e^{x^2} \cdot (x^2)’=2x\cdot e^{x^2} .\tag{Ⅴ;4及3} $$

当然，把被叠置的函数各别地写出来在事实上没有这种必要.

$9)\;y=\sin{ax} $;

$$y’_x =\cos{ax} \cdot (ax)’=a\cdot \cos{ax} .\tag{Ⅴ;7,1,2} $$

$10)\;y=(x^2+x+1)^n $;

$$y’_x =n(x^2+x+1)^{n-1} \cdot (x^2+x+1)’=n(2x+1)(x^2+x+1)^{n-1} .\tag{Ⅴ;3,例1} $$

$11)\;y=2^{\sin{x} } $;

$$y’_x =2^{\sin{x} } \cdot \ln 2 \cdot (\sin{x} )’=\ln 2 \cdot \cos{x} \cdot 2^{\sin{x} } .\tag{Ⅴ;4,6} $$

$12)\;y=\arctan{\dfrac{1}{x} } $;

$$y’_x =\dfrac{1}{1+\left( \dfrac{1}{x} \right) ^2} \cdot \left( \dfrac{1}{x} \right)’ =\dfrac{x^2}{1+x^2} \cdot \left( -\dfrac{1}{x^2} \right) =-\dfrac{1}{1+x^2} .\tag{Ⅴ;12,3} $$

碰到几层叠置的复合函数，就要毫无遗漏地逐次应用法则Ⅴ：

$13)\;y=\sqrt{\tan{\dfrac12 x} } $;于是

$$\begin{align}
y’_x & =\dfrac{1}{2\sqrt{\tan{\dfrac12 x} } } \cdot \left( \tan{\dfrac12 x} \right)’_x \tag{Ⅴ;3} \\
& = \dfrac{1}{2\sqrt{\tan{\dfrac12 x} } } \cdot \sec{} ^2 \dfrac12 x \cdot \left( \dfrac12 x\right)’_x =\dfrac{\sec{} ^2 \dfrac12 x}{4\sqrt{\tan{\dfrac12 x} } } .\tag{Ⅴ;8}
\end{align}$$

$14)\;y=e^{\sin{} ^2 \frac{1}{x} } $;在这情形

$$\begin{align}
y’_x & =e^{\sin{} ^2 \frac{1}{x} } \cdot \left( \sin{} ^2 \dfrac{1}{x} \right)’_x \tag{Ⅴ;4} \\
& =e^{\sin{} ^2 \frac{1}{x} } \cdot 2\sin{\dfrac{1}{x} } \cdot \left( \sin{1}{x} \right)’_x \tag{Ⅴ;3} \\
& =e^{\sin{} ^2 \frac{1}{x} } \cdot 2\sin{\dfrac{1}{x} } \cdot \cos{\dfrac{1}{x} } \cdot \left( \dfrac{1}{x} \right)’_x \tag{Ⅴ;6} \\
& =-\dfrac{1}{x^2} \cdot \sin{\dfrac{2}{x} } \cdot e^{\sin{} ^2 \frac{1}{x} } .\tag{Ⅴ;3}
\end{align}$$

再举几个例题来应用一切的法则：

$15)\;y=\sinh{x} =\dfrac{e^x -e^{-x} }{2} $；

$$y’=\dfrac12 [(e^x)’_x -(e^{-x})’_x] =\dfrac{e^x+e^{-x} }{2} =\cosh{x} .$$

反之，若$y=\cosh{x} $，则$y’=\sinh{x} $.最后，同$4)$那样，很易得出：

若$y=\tanh{x} =\dfrac{\sinh{x} }{\cosh{x} } $，则$y’=\dfrac{1}{\cosh{} ^2 x} ,$

又若$y=\coth{x} $，则$y’=\dfrac{1}{\sinh{} ^2 x} $.

$16)\;y=\ln (x+\sqrt{x^2+1} ) $；

$$\begin{align}
y’_x & =\dfrac{1}{x+\sqrt{x^2+1} } \cdot (x+\sqrt{x^2+1} )’_x \\
& = \dfrac{1}{x+\sqrt{x^2+1} } \cdot \left( 1+\dfrac{x}{\sqrt{x^2+1} } \right) \\
& =\dfrac{1}{\sqrt{x^2+1} } .
\end{align}$$

这结果亦可以从别的想法得出.我们已在[反函数的概念，4）]内看到，函数$y=\ln (x+\sqrt{x^2+1} ) $就是函数$x=\sinh{y} $的反函数；因此[反函数的导数]；例15；[几类最重要的函数，6°]

$$y’_x =\dfrac{1}{x’_y } =\dfrac{1}{\cosh{y} } =\dfrac{1}{\sqrt{\sinh{} ^2 y+1} } =\dfrac{1}{\sqrt{x^2+1} } .$$

$17)\;y=\dfrac{x}{a^2 \sqrt{x^2+a^2} } $；

$$y’=\dfrac{1}{a^2} \cdot \dfrac{1\cdot \sqrt{x^2+a^2} -x\cdot \dfrac{x}{\sqrt{x^2+a^2} } }{(\sqrt{x^2+a^2} )^2} =\dfrac{1}{(x^2+a^2)^{3/2} } .$$

$18)\;y=\dfrac12 \arctan{\dfrac{2x}{1-x^2} } \quad (-1 < x < 1)$；

$$y’=\dfrac12 \cdot \dfrac{1}{1+\left( \dfrac{2x}{1-x^2} \right) ^2} \cdot 2\cdot \dfrac{1\cdot (1-x^2)-x\cdot (-2x)}{(1-x^2)^2} =\dfrac{1}{1+x^2} .$$

$19)\;y=\dfrac{1}{\sqrt{b-ac} } \ln \dfrac{\sqrt{ax+b} -\sqrt{b-ac} }{\sqrt{ax+b} +\sqrt{b-ac} } $.

（我们假定：$b-ac > 0$）；

$$y’=\dfrac{1}{\sqrt{b-ac} } \left[ \dfrac{\dfrac{a}{2\sqrt{ax+b} } }{\sqrt{ax+b} -\sqrt{b-ac} } -\dfrac{\dfrac{a}{2\sqrt{ax+b} } }{\sqrt{ax+b} +\sqrt{b-ac} } \right] =\dfrac{1}{(x+c)\sqrt{ax+b} } .$$

$20)\;y=\dfrac{2}{\sqrt{ac-b} } \arctan{\sqrt{\dfrac{ax+b}{ac-b} } } $.

（此处假定：$ac-b > 0$）；

$$y’=\dfrac{2}{\sqrt{ac-b} } \cdot \dfrac{1}{1+\dfrac{ax+b}{ac-b} } \cdot \dfrac{1}{\sqrt{ac-b} } \cdot \dfrac{a}{2\sqrt{ax+b} } =\dfrac{1}{(x+c)\sqrt{ax+b} } .$$

$21)\;y=\dfrac{1}{\sqrt{a^2-b^2} } \arcsin{\dfrac{a\sin{x} +b}{a+b\sin{x} } } \quad \left( \vert b\vert < a ;-\dfrac{\pi }{2} < x < \dfrac{\pi }{2} \right) $；

$$\begin{align}
y’ =& \dfrac{1}{\sqrt{a^2-b^2} } \cdot \dfrac{1}{\sqrt{1-\left( \dfrac{a\sin{x} +b}{a+b\sin{x} } \right) ^2} }\\
& \times \dfrac{a\cos{x} \cdot (a+b\sin{x} ) -(a\sin{x} +b)\cdot b\cos{x} }{(a+b\sin{x} )^2} =\dfrac{1}{a+b\sin{x} } .\\
\end{align}$$

$22)\;y=\dfrac{1}{\sqrt{b^2-a^2} } \ln \dfrac{b+a\sin{x} -\sqrt{b^2-a^2} \cdot \cos{x} }{a+b\sin{x} } \quad (\vert a\vert < \vert b\vert )$；

$$y’=\dfrac{1}{\sqrt{b^2-a^2} } \left[ \dfrac{a\cos{x} +\sqrt{b^2-a^2} \sin{x} }{b+a\sin{x} -\sqrt{b^2-a^2} \cos{x} } -\dfrac{b\cos{x} }{a+b\sin{x} } \right] =\dfrac{1}{a+b\sin{x} } .$$

$23)$作为一个习题，我们再来研究关于幂指数式$y=u^v(u > 0)$的导数的问题，式中$u$及$v$是$x$的函数，并在所给点有导数$u’,v’$.

把等式$y=u^v$取对数，就得

$$\ln y=v\cdot \ln u.\label{5} \tag{5} $$

这样，$y$的表达式就可以改写成为$y=e^{v\ln u}$，由此已经很清楚，导数$y’$存在.它的求法还可以更简单地做出，就是使$\eqref{5} $两边的关于$x$的导数相等.这时我们利用法则Ⅴ及Ⅲ（记住$u,v$及$y$是$x$的函数），就得到

$$\dfrac{1}{y} y’=v’\cdot \ln u+v\cdot \dfrac{1}{u} \cdot u’,$$

由此

$$y’=y\left( \dfrac{vu’}{u} +v’\ln u \right) ,$$

或用$y$的表达式代换它，

$$y’=u^v \left( \dfrac{vu’}{u} +v’\ln u \right) .\label{6} \tag{6} $$

这公式是莱布尼茨和J.伯努利（Johann Bernoulli）首先建立的.

例如，若$y=x^{\sin{x} } $，则$y’=x^{\sin{x} } \left( \dfrac{\sin{x} }{x} +\cos{x} \cdot \ln u \right) $.

$24)$假定函数$f(x)$有导数$f’(x)$，写出下列函数的关于$x$的导数式

$$(а)\;\sin{f(x)},\quad (б)\;e^{f(x)},\quad (в)\;\ln f(x),$$

并写出下列函数的关于$t$的导数式

$$(г)\;f(\sin{t} ),\quad (д)\;f(e^t),\quad (е)\;f(\ln t),$$

答：

$$(а)\;\cos{f(x)} \cdot f’(x);\quad (б)\;e^{f(x)} \cdot f’(x);\quad (в)\;\dfrac{f’(x)}{f(x)} ;$$

$$(г)\;f’(\sin{t} )\cdot \cos{t} ;\quad (д)\;f’(e^t)\cdot e^t,\quad (е)\;f’(\ln t)\cdot \dfrac{1}{t} .$$

关于最后的三个例题$(г),(д),(е)$，请读者注意，记法$f’(\cdots )$表示函数$f(x)$关于它所依赖的变元$x$的导数，但在这变元的数值各为$x=\sin{t} ,e^t ,\ln t$时，$f’(\cdots )$已经依赖于$t$了.参阅[复合函数的导数]的脚注.

$25)$函数$f(x)$是在关于$0$对称的区间内定义的，若$f(-x)=f(x)$，它就称为偶函数；若$f(-x)=-f(x)$，它就称为奇函数（偶函数的例子，如偶次幂函数$x^2 ,x^4,\cdots $，以及$\cos{x} ,\cosh{x} $；奇函数的例子，如奇次幂函数$x,x^3 ,\cdots ,\sin{x} ,\sinh{x} $.）

试证明，偶函数的导数（假如存在）为奇函数，而奇函数的导数为偶函数.

证明：设可导的偶函数$f(x)$，则$f(-x)=f(x)$，两边求导，得

$$f’(-x)\cdot (-x)’=f’(x) $$

即$f’(-x)=-f’(x)$，故$f’(x)$是奇函数.

所以偶函数的导数（假如存在）为奇函数.同理可证奇函数的导数为偶函数.

$26)$求出函数$y=\ln \vert x\vert $在$x\gtrless 0$时的导数.

在$x > 0$时，显然$y’=\dfrac{1}{x} $；今将指出这公式在$x < 0$时仍为适用.实际上，把函数

$$y=\ln \vert x\vert =\ln (-x)$$

当作复合函数而求其导数，那么，在这种情形，就亦有

$$y’=\dfrac{1}{-x} \cdot (-1)=\dfrac{1}{x} .$$

$27)$考察曲线

$$y=ax^n (n > 0).$$

在其上某一点$(x,y)$处的切线的斜率是[在曲线上作切线问题]~[导数的定义]：

$$\tan{\alpha } =y’=nax^{n-1} .$$

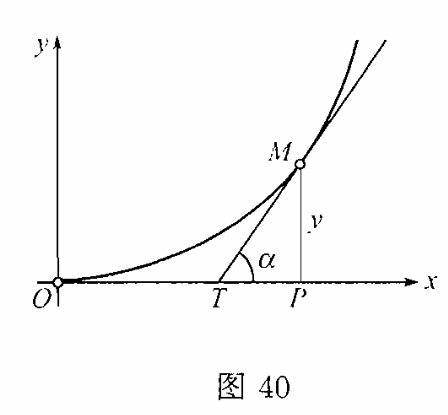
由图$40$看出，线段$TP$（所谓“次切距”）等于

$$TP=\dfrac{y}{\tan{\alpha } } =\dfrac{ax^n }{nax^{n-1} } =\dfrac{x}{n} .$$

利用这事实可得到切线的简易作图法（[在曲线上作切线问题]的结果的推广）.

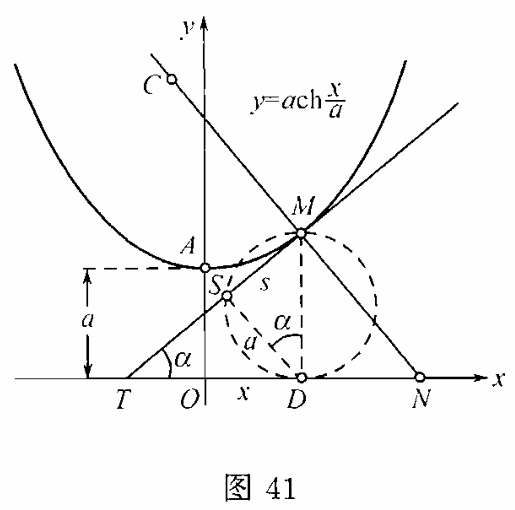
$28)$对于曲线（“悬链线”）

$$y=a\cdot \cosh{\dfrac{x}{a} } (a > 0),$$

用相似的方法，得

$$\tan{\alpha } =y’=\sinh{\dfrac{x}{a} } .$$

在这次定义（设想$x > 0$）

$$\cos{\alpha } =\dfrac{1}{\sqrt{1+\tan{} ^2 \alpha } } =\dfrac{1}{\sqrt{1+\sinh{} ^2 \dfrac{x}{a} } } =\dfrac{1}{\cosh{\dfrac{x}{a} } } =\dfrac{a}{y} ,$$

于是$y\cdot \cos{\alpha } =a$.若从纵标$y=DM$的中$D$（图$41$）作切线$MT$的垂线$DS$，则线段$DS$就等于$a$.由此再推得在所考察的曲线上作切线的简易作图法；把纵标$DM$当作直径作一半圆，以$D$为中心，$a$为直径截取交点$S$；直线$MS$就是切线.

$29)$设质点沿着一轴在某一中心点的附近依下列规律而振动：

$$S=A\cdot \sin{(\omega t+\alpha )} \quad (A,\omega > 0).$$

这种振动称为简谐运动；$A$是它的振幅，$\omega $是频率，$\alpha $是初相.

取路程$S$关于时间$t$的导数，求得运动的速度：

$$v=A\omega \cdot \cos{\omega t+\alpha } .$$

当$S=0$时，即点经过中心时，速度达到最大的数值$\pm A\omega $.反之，当点的位置离中心最远时（$S=\pm A$）速度$v=0$.

求$v$关于$t$的导数：

$$a=-A\omega ^2 \cdot \sin{(\omega t+\alpha )} $$

给出点的运动的加速度；显然

$$a=-\omega ^2 \cdot S.$$

由此，引入动点的质量$m$，依牛顿定律，若简谐振动是由于力$F$的作用而发生，则这力$F$可表示为：

$$F=-m\omega ^2 \cdot S.$$

由此看出，它永远指向中心（因为有与$S$相反的符号），并与点离中心的距离成比例.

$30)$依规律

$$S=Ae^{-kt} \sin{\omega t} \quad (A,k,\omega > 0)$$

而发生的运动称为阻尼振动，因为有因式$e^{-kt}$存在，虽则质点也在中心点附近作振动，但总是逐渐趋向于和中心点重合：

$$\lim_{t\to \infty } S=0.$$

在这种情形

$$v=S’_t =Ae^{-kt} (\omega \cdot \cos{\omega t} -k\cdot \sin{\omega t} ) $$

又

$$a=v’_t =-Ae^{-kt} (\omega ^2 \cdot \sin{\omega t} +2\omega k\cdot \cos{\omega t} -k^2 \cdot \sin{\omega t} ) .$$

再在括号内引入$\pm k^2\cdot \sin{\omega t} $，在明显的变形以后，就得

$$\begin{align}
a & =-Ae^{-kt} [(\omega ^2 +k^2)\sin{\omega t} +2k(\omega \cdot \cos{\omega t} -k\cdot \sin{\omega t} )] \\
& =-(\omega ^2 +k^2)\cdot S-2k\cdot v.
\end{align}$$

若这种振动是由于力$F$的作用而发生，则$F$等于

$$F=-(\omega ^2+k^2)m\cdot S-2km\cdot v.$$

我们看出，它是由两种力：$1)$与质点离中心的距离成正比且指向着这中心的力（同在调和振动的情形一样），及$2)$与速度成正比且与速度方向相反的阻挠运动的力，相加而成的.

单侧导数

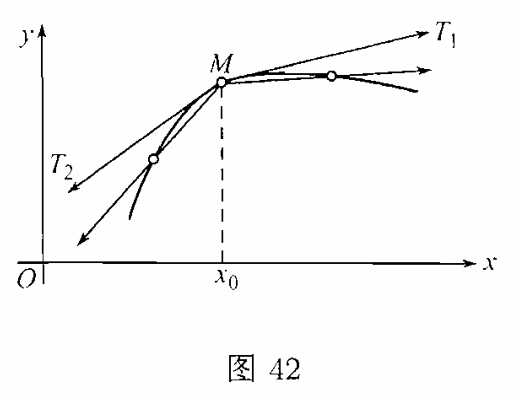
在结束这一节时，我们来考察一些关于导数可能产生的特殊情形.先从建立单侧导数的概念开始.若所考察的数值$x$就是函数$y=f(x)$的定义区间$\mathcal{X}$的端点之一，则在求比式$\dfrac{\Delta y}{\Delta x} $的极限时，$\Delta x $接近于零时就仅限于从右（当讲到区间的左端点时）或从左（右端点时）.在这种情形若极限存在，就称为右导数或左导数.函数的图像在对应点处就有单侧切线.

也可能碰到，在内点$x$处比式$\dfrac{\Delta y}{\Delta x} $仅各有单侧极限存在（在$\Delta x\to +0$或$\Delta x\to -0$时），且并不相等；它们也称为单侧导数.函数的图像在对应点处将仅有两单侧切线存在，它们组成一角；该点就是角点（图$42$）.

考察函数$y=f(x)=\vert x\vert $作为一例.从数值$x=0$出发，将有

$$\Delta y=f(0+\Delta x) -f(0)=f(\Delta x) =\vert \Delta x\vert .$$

若$\Delta x > 0$，则

$$\Delta y=\Delta x,\lim_{\Delta x\to 0} \dfrac{\Delta y}{\Delta x} =1.$$

又若$\Delta x < 0$，则

$$\Delta y=-\Delta x,\lim_{\Delta x\to 0} \dfrac{\Delta y}{\Delta x} =-1.$$

这函数的图像由第一及第二象限角的分角线所组成，原点就成为角点.

无穷导数

若增量的比式$\dfrac{\Delta y}{\Delta x} $在$\Delta x\to 0$时趋于$+\infty (-\infty )$，则这一广义的数也称为导数（且像通常那样表示着）.单侧无穷导数的概念也可类似地建立起来.导数的几何说明（作为是切线的斜率）也可推广到这一情形；但在此处，切线是平行于$y$轴的（图$43,а,б,в,г$）.

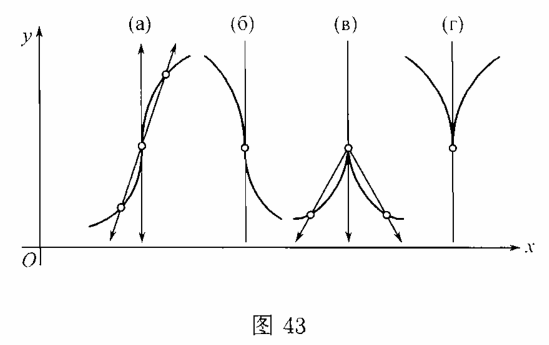
在$(а)$及$(б)$的情形，这导数各等于$+\infty $及$-\infty $（两个单侧导数符号相同），而在$(в)$及$(г)$的情形两个单侧导数符号相异.

例如，设$f_1 (x)=x^{\frac{1}{3} } $；在$x\neq 0$时，[导数公式一览表]的公式$3$给出

$$f’_1 (x)=\dfrac{1}{3} x^{-\frac{2}{3} } =\dfrac{1}{3x^{\frac{2}{3} } } ,$$

但它在$x=0$时是不能用的.我们要求在这点处的导数，就应直接从导数的定义出发；作比式

$$\dfrac{f_1 (0+\Delta x)-f_1 (0)}{\Delta x} =\dfrac{(\Delta x)^{\frac13 } }{\Delta x} =\dfrac{1}{\Delta x^{\frac23 } } ,$$

我们看出，当$\Delta x\to 0$时它的极限就是$+\infty $.同样可以相信，对于函数$f_2 (x)=x^{\frac{2}{3} } $，在$x=0$时，左导数等于$-\infty $，而右导数等于$+\infty $.

应用导数概念的推广，可以补充[反函数的导数]中关于反函数的导数的定理，指出即使在那种情形，即当$f’(x_0 )$等于$0$或$\infty $时，反函数的导数$g’(y_0 )$仍存在，而且各等于$\infty $或$0$.例如，因为函数$\sin{x}$在$x=\pm \dfrac{\pi }{2} $时有导数$\cos{\left( \pm \dfrac{\pi }{2} \right) } =0$，故反函数$\arcsin{y}$在$y=\pm 1$时有无穷导数（就是$+\infty $）存在.

特殊情形的例题

$1^{\circ } \quad $导数不存在的例题

已经说过函数$y=\vert x\vert $在点$x=0$处[参阅[单侧导数]]并无通常的双侧导数.但更有趣的是这样的例题，函数

$$f(x)=x\cdot \sin{\dfrac{1}{x} } (x\neq 0时),\quad f(0)=0,$$

在$x=0$时也是连续的[间断函数的例题]，但在这点却连单侧导数都没有.事实上，比式

$$\dfrac{f(0+\Delta x)-f(0)}{\Delta x} =\dfrac{f(\Delta x)}{\Delta x} =\sin{\dfrac{1}{\Delta x} } $$

在$\Delta x\to \pm 0$时不趋于任何极限.

由这函数的图像（图$24$）很容易看出，从原点$O$引出的割线$OM_1 $在$M_1 $趋于$O$时并无极限位置，因此曲线在原点处没有切线（即使是单侧的也没有）.

在以后[第二卷]我们将再举一个值得注意的例题，一函数在变元的一切数值时是连续的，但在其中任何数值时都没有导数.

$2^{\circ } \quad $导数间断的例题

若所给函数$y=f(x)$在某一区间$\mathcal{X} $内的每一点处有有限导数$y’=f’(x)$存在，则这导数本身也是$\mathcal{X} $内的$x$的函数.到现在为止，我们所碰到的例子内，函数$f(x)$都是连续的.然而，这也可能并不如此.例如，考察函数

$$f(x)=x^2 \cdot \sin{\dfrac{1}{x} } (x\neq 0时),\quad f(0)=0.$$

若$x\neq 0$，则用通常的方法就求出它的导数

$$f’(x)=2x\cdot \sin{\dfrac{1}{x} } -\cos{\dfrac{1}{x} } ,$$

但所得的结果在$x=0$时是不能用的.在这种情形，直接用导数概念的定义来讨论，就有

$$f’(0)=\lim_{\Delta x\to 0} \dfrac{f(0+\Delta x)-f(0)}{\Delta x} =\lim_{\Delta x\to 0} \Delta x\cdot \sin{\dfrac{1}{\Delta x} } =0.$$

同时，清楚地，$f’(x)$在$x\to 0$时并不趋于任何极限，因此在$x=0$时函数$f’(x)$有间断.

这对于任意的函数

$$f(x)=x^{\alpha } \cdot \sin{\dfrac{1}{x} } (x\neq 0时),\quad f(0)=0,$$

只要$2 > \alpha > 1$，也同样是真空的.

在这些例题内，导数的间断都是属于第二类的.这并非偶然的事件：下面[导数的极限]我们将看到，导数不能有第一类的间断，即跃度.