让我再一次回到立方体涂色问题（见第三章第$3.4$节近结束前的例子）：把立方体的六个面涂上油漆，或涂红色，或涂绿色，共有多少个不同的花式呢？我们已经计算过，共有$10$个，但当时并没有计算每种涂色花式有多少个.考虑的群是$S_6 $里的一个$24$阶子群，在第三章第$3.4$节里我们已经把它的元的圈分解全部写了出来，由此可以写下这个群的圈指标，是$(x_1^6 +6x_1^2 x_4 +3x_1^2 x_2^2 +6x_2^3 +8x_3^2 )/24$.按照波利亚计数定理，这个问题的构形计数记录是

$$\begin{align}
I(a,b) & =[(a+b)^6+6(a+b)^2(a^4+b^4)+3(a+b)^2(a^2+b^2)^2 + \\
& 6(a^2+b^2)^3+8(a^3+b^3)^2]/24 \\
& =a^6+a^5b+2a^4b^2+2a^3b^3+2a^2b^4+ab^5+b^6 ,
\end{align}$$

$a$代表红，$b$代表绿.六面涂红色的有一个花式、五面涂红色的有一个花式、四面涂红色的有两个花式、三面涂红色的有两个花式、两面涂红色的有两个花式、一面涂红色的有一个花式、没有一面涂红色的有一个花式，合起来共有$10$个花式.如果用逐面相隔的横直彩色线代替整面涂色，那么考虑的群缩小了，是$S_6$里的一个$12$阶子群，只占刚才那个群的一半元，它的圈指标是$(x_1^6 +3x_1^2 x_2^2 +8x_3^2 )/12$，于是构形计数记录是

$$\begin{align}
I(a,b) & =[(a+b)^6+3(a+b)^2(a^2+b^2)^2 +8(a^3+b^3)^2]/12 \\
& =a^6+a^5b+2a^4b^2+4a^3b^3+2a^2b^4+ab^5+b^6 ,
\end{align}$$

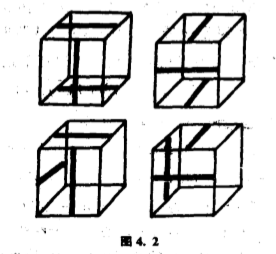
六面画红线的有一个花式、五面画红线的有一个花式、四面画红线的有两个花式、三面画红线的有四个花式、两面画红线的有两个花式、一面画红线的有一个花式、没有一面画红线的有一个花式，合起来共有$12$个花式.这个计算也清楚地显示了那多出的两个花式怎样产生，它们都有三面红线和三面绿线（图$4.2$）.

第二个例子是第一章第$1.1$节和第$1.3$节的问题：如果苯的结构中六个碳原子排成一个正六边形，当两个氢原子（以$c$代表）各给换成两个基（以$a$和$b$代表），有多少个同分异构体呢？如果苯的结构中六个碳原子排成一个三棱柱体，答案有没有不同？头一个情况涉及的群是$D_6$，它的圈指标是$(x_1^6 +4x_2^3 +2x_3^2 +3x_1^2 x_2^2 +2x_6 )/12$，从而得出构形计数记录是

$$\begin{align}
I(a,b,c) & =[(a+b+c)^6+4(a^2+b^2+c^2)^3+2(a^3+b^3+c^3)^2+ \\
& 3(a+b+c)^2(a^2+b^2+c^2)^2 +2(a^6+b^6+c^6)]/12,
\end{align}$$

在上一节里我们已经计算了，$abc^4$的系数是$3$.第二个情况涉及的群是$S_6$里的一个$6$阶子群，圈的指标是$(x_1^6+3x_2^3+2x_3^2)/6$，从而得出构形计数记录是

$$I(a,b,c)=[(a+b+c)^3+3(a^2+b^2+c^2)^3+2(a^3+b^3+c^3)^2]/6,$$

$abc^4$这一项的系数是$5$.如果读者还未感到筋疲力倦的话，大可计算正八面体的情况，验证一下$abc^4$在那个构形计数记录中的系数是不是$2$.

第三个例子是第一章第$1.4$节的开关电路问题：如果容许调换输入，需要多少个开关电路便可以实现全部开关电路呢？先看最简单的情况，只有两个输入和一个输出，$S$的元是定义在全部四个二元有序偶$(z_1 ,z_2 )$上的函数，取值$0$（以$y$代表）或$1$（以$x$代表）.应该考虑的群是调换输入后导致的置换群，它是$S_4 $里的一个$2$阶子群.如果我们以$0$代$(0,0)$、$1$代$(0,1)$、$2$代$(1,0)$和$3$代$(0,0)$，那么不调换输入导致的群元就是$\begin{pmatrix} 0 & 1 & 2 & 3 \\ 0 & 1 & 2 & 3 \end{pmatrix} $，输入经对换后（即从$(z_1 ,z_2 )$变成$(z_2 ,z_1 )$）导致的群元就是$\begin{pmatrix} 0 & 1 & 2 & 3 \\ 0 & 2 & 1 & 3 \end{pmatrix} $.这个二元群作用在$S$上得来的轨，便是起码应具备的二元函数类，也即是起码需要设计的开关电路了.这个群的圈指标是$(x_1^4+x_1^2 x_2 )/2$，构形计数记录是

$$\begin{align}
I(y,x) & =[(y+x)^4+(y+x)^2(y^2+x^2)]/2 \\
& =y^4+3y^3x+4y^2x^2+3yx^3+x^4 ,
\end{align}$$

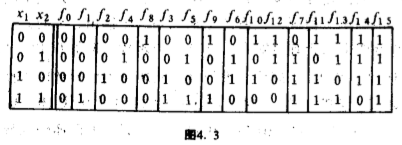
意思是说，不取值$1$的函数类有一个、取值$1$一次的函数类有三个、取值$1$两次的函数类有四个、取值$1$三次的函数类有三个、取值$1$四次的函数类有一个，合起来共有$12$个（图$4.3$）.

如果开关电路有三个输入和一个输出，应该考虑的群比前一个较在，是$S_8$里的一个$6$阶子群，有兴趣的读者可以试着计算它的圈指标，应是$(x_1^8 +3x_1^4 x_2^2 +2x_1^2 x_3^2 )/6$，所以构形计数记录是

$$\begin{align}
I(y,x) & =[(y+x)^8+3(y+x)^4(y^2+x^2)^2+2(y+x)^2(y^3+x^3)^2]/6 \\
& =y^8+4y^7x+9y^6x^2+16y^5x^3+20y^4x^4+16y^3x^5+9y^2x^6+4yx^7+x^8 ,
\end{align}$$

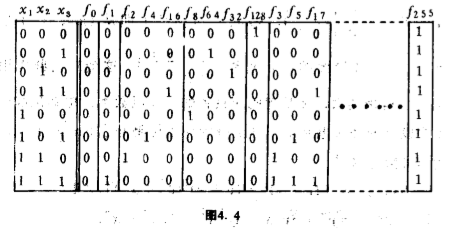
共需用$80$个二元函数类，其中不取值$1$的函数类有一个、取值$1$一次的函数类有四个、取值$1$二次的函数类有九个$\cdots $取值$1$八次的函数类有一个（图$4.4$）.

如果更容许某些输入通过非门，应该考虑的群便更大，需用的二元函数类便更少.举两个输入和一个输出的情况为例，刚才的群有两个元，就是$\begin{pmatrix} 0 & 1 & 2 & 3 \\ 0 & 1 & 2 & 3 \end{pmatrix} $和$\begin{pmatrix} 0 & 1 & 2 & 3 \\ 0 & 2 & 1 & 3 \end{pmatrix} $，现在每个元可以衍生四个元，这是因为$(z_1 ,z_2 )$可以变成$(z_1 ,z_2 )$、或$(\overline{z}_1 ,z_2 )$、或$(z_1 ,\overline{z}_2 )$、或$(\overline{z}_1 ,\overline{z}_2 )$，加上横杠表示$0$和$1$的值对换了.从$\begin{pmatrix} 0 & 1 & 2 & 3 \\ 0 & 1 & 2 & 3 \end{pmatrix} $得来的元是$\begin{pmatrix} 0 & 1 & 2 & 3 \\ 0 & 1 & 2 & 3 \end{pmatrix} $，$\begin{pmatrix} 0 & 1 & 2 & 3 \\ 2 & 3 & 0 & 1 \end{pmatrix} $，$\begin{pmatrix} 0 & 1 & 2 & 3 \\ 1 & 0 & 3 & 2 \end{pmatrix} $，$\begin{pmatrix} 0 & 1 & 2 & 3 \\ 3 & 2 & 1 & 0 \end{pmatrix} $；从$\begin{pmatrix} 0 & 1 & 2 & 3 \\ 0 & 2 & 1 & 3 \end{pmatrix} $得来的元是$\begin{pmatrix} 0 & 1 & 2 & 3 \\ 0 & 2 & 1 & 3 \end{pmatrix} $，$\begin{pmatrix} 0 & 1 & 2 & 3 \\ 2 & 0 & 3 & 1 \end{pmatrix} $，$\begin{pmatrix} 0 & 1 & 2 & 3 \\ 1 & 3 & 0 & 2 \end{pmatrix} $，$\begin{pmatrix} 0 & 1 & 2 & 3 \\ 3 & 1 & 2 & 0 \end{pmatrix} $.应该考虑的群是$S_4$里的一个$8$阶子群，它的圈指标是$(x_1^4 +3x_2^2 +2x_1^2 x_2 +2x_4 )/8$，代入波利亚计数公式，构形计数记录是

$$\begin{align}
I(y,x) & =[(y+x)^4+3(y^2+x^2)^2+2(y+x)^2(y^2+x^2)+2(y^4+x^4)]/8 \\
& =y^4+y^3x+2y^2x^2+yx^3+x^4 ,
\end{align}$$

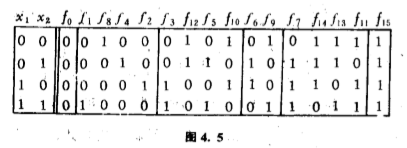
因此，如果容许调换输入又容许某些输入通过非门的话，我们只用设计$6$个开关电路便能实现全部$16$个开关电路了（图$4.5$）.

读者有没有兴趣试一试三个输入和一个输出的情况呢？你猜需要多少个开关电路便能实现全部$2^8=256$个开关电路呢？惯于深究的读者自然会问：$N$个输入和一个输出的情况怎样？波利亚早于$1940$年的一篇文章里便提出这个问题，他指出问题相当于以下的构形计数问题：把一个$N$维立方体的$2^N$个端点涂上黑色或白色，共有多少个不同的花式？利用他的计数公式，问题化为计算$N$维立方体的对称群的圈指标.史立派安（$\mathrm{D.Slepian}$）在$1953$年找着一个答案，但目前最有效的算法当推罗宾逊（$\mathrm{R.W.Robinson}$）和巴尔马（$\mathrm{E.M.Palmer}$）在$1969$年发表的理论，见诸：E.M.Palmer.The exponentiation group as the automorphism group of a graph,in “Proof techniques in graph theory”,F.Harary(ed.).New York:Academic Press,$1969\colon 125-131$.

最后，让我举一个关于图的计数问题来结束本节的讨论.这里我们只讨论单图，即是一些点（叫做图的端点）和一些连接某些点的线（叫做图的边）的组合，但两点之间顶多只有一条线连接，也没有线连接同一个点（用图论的术语说，是没有重边或自身圈）.对一个图，我们只对点的邻接关系感兴趣，有线连接的点叫做邻接的点.至于怎样摆放那些点和怎样画那些连接点的线，我们是不关心的.比方下面的两个图，虽然看去样子极不相似，我们却不区分，把它们当做是同样的图，更正确的说法，它们是同构的图（图$4.6$）.

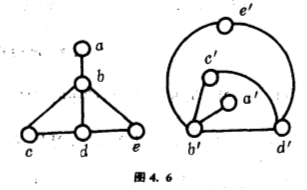
现在的问题是：共有多少个互相不同构的$N$个端点的单图？一个端点的单图只有一个，两个端点的单图有两个，三个端点的单图有四个，这都不难看得出来，但端点数目增大，凭手画画数数便很困难了！

让我们先把单图计数问题纳入第三章第$3.4$节的架构.把每个端点标号，设为$a_1 $、$\cdots $、$a_N$，每个无序偶$\lbrace a_i ,a_j \rbrace $表示一对端点，或有线连接，或无线连接.如果是有线连接，我们定义函数值$f(\lbrace a_i ,a_j \rbrace )=x$；如果是没有线连接，我们定义函数值$f(\lbrace a_i ,a_j \rbrace )=y$.于是有一个标号端点的图相应于一个从$C=\lbrace 1,2,\cdots ,N(N-1)/2 \rbrace $到$\lbrace x,y\rbrace $的函数.下一个问题是：同构的图应该如何从这些有标号端点的图进行分类得来呢？两个图同构，相当于把图的有标号端点调换次序后，不变更邻接关系.应该考虑的群，是从端点的置换导致的边的置换群，让我举$N=3$为例作说明.三个端点的置换组成$S_3 $，它的六个元是

$$\begin{pmatrix} a_1 & a_2 & a_3 \\ a_1 & a_2 & a_3 \end{pmatrix} ,\begin{pmatrix} a_1 & a_2 & a_3 \\ a_1 & a_3 & a_2 \end{pmatrix} ,\begin{pmatrix} a_1 & a_2 & a_3 \\ a_2 & a_1 & a_3 \end{pmatrix} ,$$

$$\begin{pmatrix} a_1 & a_2 & a_3 \\ a_2 & a_3 & a_1 \end{pmatrix} ,\begin{pmatrix} a_1 & a_2 & a_3 \\ a_3 & a_1 & a_2 \end{pmatrix} ,\begin{pmatrix} a_1 & a_2 & a_3 \\ a_3 & a_2 & a_1 \end{pmatrix} ,$$

从三个端点得出的无序偶有三个，就是$\lbrace a_1 ,a_2 \rbrace $、$\lbrace a_1 ,a_3 \rbrace $和$\lbrace a_2 ,a_3 \rbrace $，为简便起见，分别记作$1$、$2$、$3$.第一个元导致的边的置换是$\begin{pmatrix} 1 & 2 & 3 \\ 1 & 2 & 3 \end{pmatrix} =(1)(2)(3)$、第二个元导致的边的置换是$\begin{pmatrix} 1 & 2 & 3 \\ 2 & 1 & 3 \end{pmatrix} =(3)(1,2)$、第三个元导致的边的置换是$\begin{pmatrix} 1 & 2 & 3 \\ 1 & 3 & 2 \end{pmatrix} =(1)(2,3)$、第四个元导致的边的置换是$\begin{pmatrix} 1 & 2 & 3 \\ 3 & 1 & 2 \end{pmatrix} =(1,3,2)$，第五个元导致的边的置换是$\begin{pmatrix} 1 & 2 & 3 \\ 2 & 3 & 1 \end{pmatrix} =(1,2,3)$，第六个元导致的边的置换是$\begin{pmatrix} 1 & 2 & 3 \\ 3 & 2 & 1 \end{pmatrix} =(2)(1,3)$.端点的置换群的圈指标是$(x_1^3 +3x_1 x_2 +2x_3 )/6$，它导致的边的置换群的圈指标也是$(x_1^3 +3x_1 x_2 +2x_3 )/6$.当然，这是因为从三个端点得出三个无序偶，我们根本无须计算也知道有这样的结果.但一般而言，端点的置换群的圈指标（也即是$S_N$的圈指标）跟它导致的边的置换群的圈指标并不相同，后一个群只是$S_{N(N-1)/2}$里的一个$N!$阶子群.读者可试按照刚才的方法计算$N=4$的情况，端点置换群是$S_4 $，它的圈指标是$(x_1^4 +6x_1^2 x_2 +8x_1 x_3 +3x_2^2 +6x_4 )/24$，它导致的边的置换群是$S_6 $里的一个$24$阶子群，圈指标是$(x_1^6 +6x_1^2 x_2^2 +8x_3^2 +3x_1^2 x_2^2 +6x_2 x_4 )/24=(x_1^6 +9x_1^2 x_2^2 +6x_2 x_4 +8x_3^2 )/24$.要计算三个端点的单图的个数，只须代入波利亚计数公式，构形计数记录是

$$\begin{align}
I(x,y) & =[(x+y)^3+3(x+y)(x^2+y^2)+2(x^3+y^3)]/6 \\
& =x^3 +x^2y+xy^2 +y^3 ,
\end{align}$$

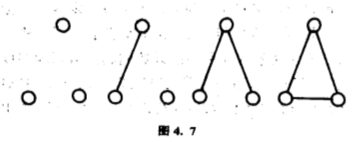
意思是说，共有$4$个三个端点的单图，其中含三条边、两条边、一条边、没有边的各占一个（图$4.7$）.

要计算四个端点的单图的个数，是依样画葫芦，代入波利亚计算公式，得到构形计数记录

$$\begin{align}
I(x,y) & =[(x+y)^6+9(x+y)^2(x^2+y^2)^2+6(x^2+y^2)(x^4+y^4)+8(x^3+y^3)^2]/24 \\
& =x^6 +x^5y+2x^4y^2 +3x^3y^3 +2x^2y^4+xy^5 +y^6 ,
\end{align}$$

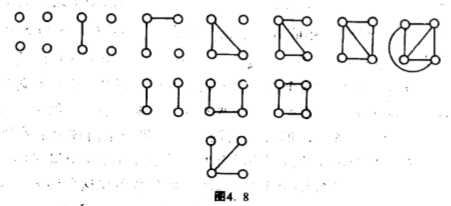
共有$11$个单图，其中含六条边的有一个、含五条边的有一个、含四条边的有两个、含三条边的有三个、含两条边的有两个、含一条边的有一、没有边的有一个（图$4.8$）.

惯于深究的读者又问：$N$个端点的单图有多少个？根据波利亚公式，这个问题化为计算从$S_N$导致的边的置换群的圈指标，经仔细分析这条公式是可以写下来的，但公式看起来是十分臃肿，在这里我不写出来了.波利亚早便意识到他的计数公式足以应付这方面的问题，但他没有发表，只把他的意见告诉给哈拉利，哈拉利在$1955$年发表了一篇文章，运用波利亚计数公式解决了好几种图的计数问题.有兴趣的读者，可以参阅哈拉利和巴尔马的专著：F.Harary,E.M.Palmer.Graphical enumeration.New York:Academic Press,$1973$.