第三章第$3.4$节介绍了一个相当广泛的架构；$S$是全部从$C=\lbrace 1,\cdots ,N\rbrace $到$R=\lbrace r_1 ,\cdots ,r_m \rbrace $的映射$f$组成的集合，$G$是$N$次对称群$S_N$里某个子群；对$G$中元$\pi $与$S$中元$f$，规定$\pi \ast f$是$f\pi $，这定义了一个$G$在$S$上的作用；伯氏引理让我们计算在这个作用下的轨的个数.可是，有些问题却需要在这个架构上添加少许花絮才应付得来.举一个例子：有三只标以$A$、$B$、$C$的桶，把两个黑球和一个白球分放在桶里，有多少个不同的放置方法呢？在第三章第$3.4$节里我们已经计算了一个同类型的问题，球的个数和颜色比这个还多.应该考虑的群是个二元群，元是$\begin{pmatrix} 1 & 2 & 3 \\ 1 & 2 & 3 \end{pmatrix}$和$\begin{pmatrix} 1 & 2 & 3 \\ 2 & 1 & 3 \end{pmatrix}$，$R=\lbrace A,B,C\rbrace $.运用伯氏引理，便知道轨的个数是$(3^3+3^2)/2=18$，也就是说，共有$18$个不同的放置方法.如果我们运用波利亚计数定理，知道的就更详尽了，构形计数记录是

$$\begin{align}
I(A,B,C) & =[(A+B+C)^3+(A+B+C)(A^2+B^2+C^2)]/2 \\
& =A^3+2A^2B+2A^2C+2AB^2+2AC^2+3ABC+B^3+2B^2C+2BC^2+C^3,
\end{align}$$

它显示了球在桶内的分布（图$4.9$）.

假定桶$B$和桶$C$的标签脱落了，两个桶无从分辨出来，那么共有多少个不同的放置方法呢？察看那$18$个放置方法，我们知道有好些变成是相同的，例如两个黑球放在桶$A$、一个白球放在桶$B$，跟两个黑球放在桶$A$、一个白球放在桶$C$，两者是区分不出的.其实，那$18$个放置方法缩减为$10$个而已（图$4.10$）.

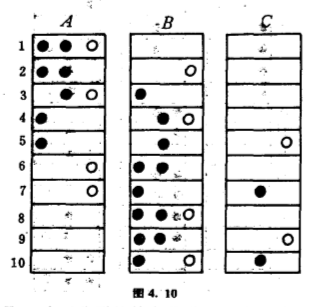
为什么会有这个不同的答案呢？关键在哪儿？按照伯氏引理的思路，我们会想到除了$G$在集合$C$上的作用带来$G$在集合$S$上的作用以外，还有另一个群$H$在集合$R$上的作用也对最后集合$S$上的作用产生影响，变更了由此得到的轨.在刚才的问题里，$H$是由$\begin{pmatrix} A & B & C \\ A & B & C \end{pmatrix}$和$\begin{pmatrix} A & B & C \\ A & C & B \end{pmatrix}$组成的二元群.希望这个例子为读者提供了一种感性认识，现在让我们开始把它写成精确的数学形式吧.

设$G$是$N$次对称群$S_N$的某个子群，$H$是$m$次对称群$S_m$的某个子群.$(G,H)$是一个这样的群，它的元是有序偶$(\alpha ,\beta )$，其中$\alpha $是$G$的元，$\beta $是$H$的元；$(\alpha ,\beta )$和$(\alpha’ ,\beta’ )$的乘积定义作$(\alpha ,\beta )(\alpha’ ,\beta’ )=(\alpha’ \alpha ,\beta \beta’ )$.（请注意，由于乘法定义不同，$(G,H)$并不是在第二章第$2.6$节提过的$G$和$H$的直积！）仍设$S$是全部从$C=\lbrace 1,2,\cdots ,N\rbrace $到$R=\lbrace r_1 ,\cdots ,r_m \rbrace $的映射$f$组成的集合，对$(G,H)$中元$(\alpha ,\beta )$与$S$中元$f$，规定$(\alpha ,\beta )\ast f=\beta f\alpha $，这定义了一个$(G,H)$在$S$上的作用，读者可以自行验证；我们要计算的是这个作用下的轨的个数.或者回头看看开首的例子，了解一下什么构成这个作用下的轨.取$G=\left\lbrace \begin{pmatrix} 1 & 2 & 3 \\ 1 & 2 & 3 \end{pmatrix} ,\begin{pmatrix} 1 & 2 & 3 \\ 2 & 1 & 3 \end{pmatrix}\right\rbrace $，$\alpha =\begin{pmatrix} 1 & 2 & 3 \\ 2 & 1 & 3 \end{pmatrix}$；取$H=\left\lbrace \begin{pmatrix} A & B & C \\ A & B & C \end{pmatrix} ,\begin{pmatrix} A & B & C \\ A & C & B \end{pmatrix}\right\rbrace$.$\alpha $表示$1$和$2$作对换（这点反映了$1$号球和$2$号球同是黑色，分辨不出来），$\beta $表示$B$和$C$作对换（这点反映了桶$B$和桶$C$分辨不出来）.对$f=\begin{pmatrix} 1 & 2 & 3 \\ A & B & A \end{pmatrix}$，经$(\alpha ,\beta )$的作用，得到

$$\begin{pmatrix} A & B & C \\ A & C & B \end{pmatrix} \begin{pmatrix} 1 & 2 & 3 \\ A & B & A \end{pmatrix} \begin{pmatrix} 1 & 2 & 3 \\ 2 & 1 & 3 \end{pmatrix} =\begin{pmatrix} 1 & 2 & 3 \\ C & A & A \end{pmatrix} .$$

那就是说：原来的摆法是桶$A$盛$1$号球（黑球）和$3$号球（白球）、桶$B$盛$2$号球（黑球）；把$1$和$2$作对换、$B$和$C$作对换，得来的摆法是桶$A$盛$2$号球（黑球）和$3$号球（白球）、桶$C$盛$1$号球（黑球）.这两个摆法，在表面上是区分不出来的，大家都是桶$A$盛一个黑球和白球、另一个桶盛一个黑球、余下的桶没有盛球（图$4.11$）.

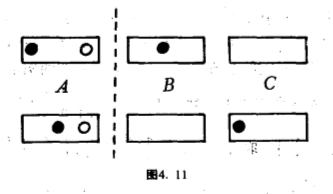
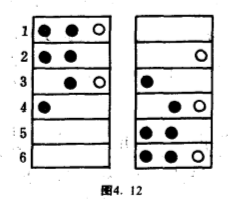
计算这个作用下的轨的个数，等于问：把两个黑球和一个白球分放在桶$A$和另外两只不能分辨的桶，有多少个不同的放置方法呢？答案是$10$个（图$4.10$）.有一点要请读者小心，在这个例子里$H$的作用并不相当于把三只桶看成是两只桶.如果问题是把那三个球分放在两只可分辨的桶，答案并不是$10$个，只是$6$个而已（图$4.12$）.

由于问题是关于球和桶，读者肯定不会混淆上述两回事，但如果我们把同一个问题换一个叙述形式，那大家便得小心了.比如说，有一个倒转三角形，端点上放置红球、黄球或绿球，如果容许把三角形绕着穿过底点的中线作轴翻转的话，共有多少个不同的花式呢？读者想一想，便知道这个问题基本上跟上一个例子没有分别，答案自然也是$18$个（图$4.13$）.

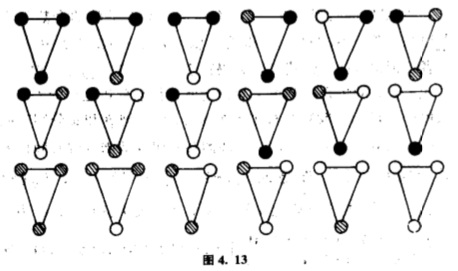
现在，我们增多一项条件，就是容许黄球和绿球调换，那么只用多少个不同的花式呢？这个问题基本上即是上一个例子的后一种情况，答案自然又是$10$个（图$4.14$）.

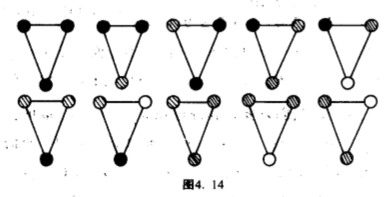
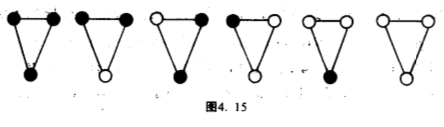
但那并不等于说我们不区分黄球和绿球，否则便变成只考虑两种颜色球，答案不是$10$个，只是$6$个而已（图$4.15$）.

根据伯氏引理，在$(G,H)$作用下$S$的轨的个数等于$\sum \vert X(\alpha ,\beta )\vert /\vert G\vert \vert H\vert $，求和式中$(\alpha ,\beta )$走遍$(G,H)$中元.读者还记得$X(\alpha ,\beta )$代表什么吗？它是全部满足$\beta f\alpha =f$的$S$中元$f$组成的集合.剩下来的事情就是仔细分析这样的$f$是什么模样，目标是数数共有多少个这样的$f$.把$\beta $和$\alpha $分别写成它们的圈分解.$\alpha $的逆元$\alpha ^{-1}$的圈分解跟$\alpha $的圈分解有同样款式的圈长分布，即是说$l_1 (\alpha )=l_1 (\alpha ^{-1})$、$\cdots $、$l_N (\alpha )=l_N (\alpha ^{-1})$.其实只要把$\alpha $的圈逐个倒转过来就是了，比方

$$\begin{align}
\alpha & =\begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 \\ 3 & 8 & 6 & 9 & 10 & 1 & 4 & 2 & 5 & 7 \end{pmatrix} \\
& =(1,3,6)(2,8)(4,9,5,10,7),
\end{align}$$

那么

$$\begin{align}
\alpha & =\begin{pmatrix} 3 & 8 & 6 & 9 & 10 & 1 & 4 & 2 & 5 & 7 \\ 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 \end{pmatrix} \\
& =(6,3,1)(8,2)(7,10,5,9,4).
\end{align}$$

假定$(a_1 ,\cdots ,a_k )$是$\alpha ^{-1}$的一个圈，而$f(a_1 )=b_1 $，$b_1 $落在$\beta $的一个圈$(b_1 ,b_2 ,\cdots ,b_l )$里.由于考虑中的$f$满足$\beta f=f\alpha ^{-1}$，我们只要计算两边在$a_1 $、$\cdots $、$a_k $取的值便知道$f(a_1 )=b_1 $、$f(a_2 )=b_2 $、$\cdots $，而且$k$一定是$l$的倍数.设$k=tl$，那么$f(a_1 )=b_1 $、$\cdots $、$f(a_l )=b_l $、$f(a_{l+1} )=b_1 $、$\cdots $、$f(a_{2l} )=b_l $、$f(a_{2l+1} )=b_1 $、$\cdots $、$f(a_{3l} )=b_l $、$\cdots $、$f(a_{tl} )=b_l $.就是说，$f$把$\alpha ^{-1}$里每个圈的元对应到$\beta $里某个圈的元，而且前一个圈的长是后一个圈的长的倍数，对应的元也就按循环次序重复这个倍数那么多次.反过来说，这样的$f$满足$\beta f=f\alpha ^{-1}$，落在$X(\alpha ,\beta )$里.举一个例子，设$\alpha ^{-1}$有一个圈是$(1,2,3,4,5,6)$（也即是说$\alpha $有一个圈是$(6,5,4,3,2,1)$），而$\beta $有一个圈是$(A,B,C)$，从这两个圈可以得到满足条件的$f$是

$$\begin{pmatrix}1 & 2 & 3 & 4 & 5 & 6 \\ A & B & C & A & B & C \end{pmatrix} ,\begin{pmatrix}1 & 2 & 3 & 4 & 5 & 6 \\ B & C & A & B & C & A \end{pmatrix} ,$$

$$\begin{pmatrix}1 & 2 & 3 & 4 & 5 & 6 \\ C & A & B & C & A & B \end{pmatrix} ,$$

如果$\beta $也有一个圈是$(C,D)$，便可以再多得到一些满足条件的$f$，是$\begin{pmatrix}1 & 2 & 3 & 4 & 5 & 6 \\ C & D & C & D & C & D \end{pmatrix}$，$\begin{pmatrix}1 & 2 & 3 & 4 & 5 & 6 \\ D & C & D & C & D & C \end{pmatrix}$.总的来说，$f$在$X(\alpha ,\beta )$的充要条件是：$f$把$\alpha ^{-1}$的圈分解里每个圈$A$的元对应到$\beta $的圈分解里圈$B$的元，其中$B$的长度$A$的长度的因子，而且按循环次序作对应.因此，只要知道$\alpha ^{-1}$（或$\alpha $）和$\beta $的圈分解里的圈长分布，便能轻易计算$\vert X(\alpha ,\beta )\vert $.

设$\alpha $有$l_k (\alpha )$个圈长为$k$的圈，而$\beta $有$l_{j(1)} (\beta )$个长为$j(1)$的圈、$l_{j(2)} (\beta )$个长为$j(2)$的圈、$\cdots $，这里的$j(1),j(2)\cdots $走遍$k$的因子.那么，对每个$\alpha $的圈分解里长为$k$的圈，共有$j(1)l_{j(1)} (\beta )\times j(2)l_{j(2)} (\beta ) \times \cdots $个不同取值方法，于是对全部$l_k (\alpha )$个圈便有$\left( \sum jl_j (\beta )\right) ^{l_k (\alpha )}$个不同取值方法，求和式中$j$走遍$k$的因子.再考虑全部圈，便知道$\vert X(\alpha ,\beta )\vert $等于$\prod \left( \sum jl_j (\beta )\right) ^{l_k (\alpha )}$了，这里头一个符号$\prod $表示乘积，$k$从$1$走到$N$，而对每个$k$，里面的求和式走遍$k$的因子（但不大于$m$）.对初次面对这样的式子的读者，这个式也许有点“拒人千里之外”的味道，让我以本节开首的问题为例作个说明吧.设$\alpha =\begin{pmatrix}1 & 2 & 3 \\ 1 & 2 & 3 \end{pmatrix} =(1)(2)(3)$和$\beta =\begin{pmatrix}A & B & C \\ A & B & C \end{pmatrix} =(A)(B)(C)$，有$l_1 (\alpha )=3$，$l_2 (\alpha )=0$，$l_3 (\alpha )=0$和$l_1 (\beta )=3$，$l_2 (\beta )=0$，$l_3 (\beta )=0$.按照上述计算，$\vert X(\alpha ,\beta )\vert $是

$$[l_1 (\beta )]^{l_1 (\alpha )} [l_1 (\beta )+2 l_2 (\beta )]^{l_2 (\alpha )} [l_1 (\beta )+3l_3 (\beta )]^{l_3 (\alpha )} ,$$

乘积中后两项都是$1$，而头一项是$3^3=27$.再设$\alpha =\begin{pmatrix}1 & 2 & 3 \\ 1 & 2 & 3 \end{pmatrix} =(1)(2)(3)$和$\beta =\begin{pmatrix}A & B & C \\ A & C & B \end{pmatrix} =(A)(B,C)$，有$l_1 (\alpha )=3$，$l_2 (\alpha )=0$，$l_3 (\alpha )=0$和$l_1 (\beta )=1$，$l_2 (\beta )=1$，$l_3 (\beta )=0$，代入上式，得到$\vert X(\alpha ,\beta )\vert $是$1^3=1$.再设$\alpha =\begin{pmatrix}1 & 2 & 3 \\ 2 & 1 & 3 \end{pmatrix} =(3)(1,2)$和$\beta =\begin{pmatrix}A & B & C \\ A & B & C \end{pmatrix} =(A)(B)(C)$，有$l_1 (\alpha )=1$，$l_2 (\alpha )=1$，$l_3 (\alpha )=0$和$l_1 (\beta )=3$，$l_2 (\beta )=0$，$l_3 (\beta )=0$，代入上式，得到$\vert X(\alpha ,\beta )\vert $是$3^1 \times 3^1=9$.最后设$\alpha =\begin{pmatrix}1 & 2 & 3 \\ 2 & 1 & 3 \end{pmatrix} =(3)(1,2)$和$\beta =\begin{pmatrix}A & B & C \\ A & C & B \end{pmatrix} =(A)(B,C)$，有$l_1 (\alpha )=1$，$l_2 (\alpha )=1$，$l_3 (\alpha )=0$和$l_1 (\beta )=1$，$l_2 (\beta )=1$，$l_3 (\beta )=0$，代入上式，得到$\vert X(\alpha ,\beta )\vert $是$1^1 \times 3^1=3$.因此，轨的个数等于$(27+1+9+3)/(2\times 2)=10$，即是说不同的放置方法共有$10$个.

圈指标把整个群里的元的圈分解圈长分布作一个详尽罗列，以上的计算会叫人意会到答案既然与那些$\alpha $与$\beta $的圈长分布有关，它应该能用圈指标表达出来.的确，荷兰数学家德布鲁恩（N.G.de Bruijn）在$1959$年发现了一个这样的公式，当$H$是单元群时，它简化为伯氏引理.公式中的思想就是以上的计算，这儿就不重复了.后来德布鲁恩继续把这个思想发挥，写了一篇文章，有兴趣的读者可以参阅：N.G.de Bruijn.A survey of generalizations of P$\mathrm{\acute{o}}$lya’s enumeration theorem.Nieuw Archief voor Wiskunde(2)，$1971$ XIX$\colon 89-112$.波利亚计数定理也有类似的推广，但涉及的计算自然是更繁复了.在$1965$年哈拉利和巴尔马研究了更一般的情况，他们的理论涵盖了波利亚和德布鲁恩理论的精华，有兴趣的读者可以参阅：F.Harary.E.M.Palmer.The power group enumeration theorem,Journal of Combinatorial Theory,$1966(1)\colon 157-173$.我们在这本小书里就不叙述这些推广了.波利亚计数定理还可以从别的角度考虑，从而把它推广.一个方向是利用组合数学里另一件有力工具——麦比乌斯反演（$\mathrm{M\ddot{o} bius\;inversion}$）——去计算一般有限群作用下的轨，另一个方向是把波利亚定理纳入群不变量理论的架构，变成是某条定理的特殊情况.这些结果都远超越了这本小书的讨论范围，我们不叙述了，有兴趣的读者可以参阅：A.Kerber.Enumeration under finite group action:Symmetry classes of mappings,in”Combinatoire $\mathrm{\acute{e} }$numerative”,G.Labelle,P.Leroux(ed.).New York:Springer-Verlag,$1986\colon 160-176$；R.Stanley.Invariants of finite groups and their applications to combinatorics.Bulletin(New series)of the American Mathematical Society,$1979(1)\colon 475-511$.

结束本节（也是本章）之前，让我回到第$4.2$节讨论过的开关电路，运用德布鲁恩的计算方法解决以下的问题.我们已经找出：如果容许调换输入和容许某些输入通过非门，需要设计多少个开关电路？比方有两个输入和一个输出，答案是$6$个（图$4.5$）.现在我们更容许输出也通过非门，需要多少个开关电路呢？仍然以两个输入和一个输出的情况为例子.在第$4.2$节里我们已经计算了，应该考虑的群$G$的圈指标是$(x_1^4 +3x_2^2 +2x_1^2 x_2 +2x_4 )/8$.由于我们容许输出通过非门，需要引入另一个群$H$，是个二元群，圈的指标是$(x_1^2 +x_2 )/2$.根据上面的计算（$N=4,m=2$），

$$\begin{align}
\vert X(\alpha ,\beta )\vert = & [l_1 (\beta )]^{l_1 (\alpha )} [l_1 (\beta )+2 l_2 (\beta )]^{l_2 (\alpha )} \cdot \\
& [l_1 (\beta )]^{l_3 (\alpha )} [l_1 (\beta )+2l_2 (\beta )]^{l_4 (\alpha )} .
\end{align}$$

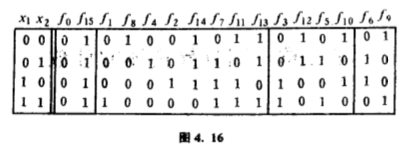
本来要计算$16$项这样的$\vert X(\alpha ,\beta )\vert $，但从圈指标中看到，其实只用计算$8$种吧.当$\alpha =(\underline{} )(\underline{} )(\underline{} )(\underline{} )$和$\beta =(\underline{} )(\underline{} )$时，$l_1 (\alpha )=4$，$l_2 (\alpha )=l_3 (\alpha )=l_4 (\alpha )=0$和$l_1 (\beta )=2$，$l_2 (\beta )=0$，所以$\vert X(\alpha ,\beta )\vert =2^4=16$；当$\alpha =(\underline{} \underline{} )(\underline{} \underline{} )$和$\beta =(\underline{} )(\underline{} )$时，$l_1 (\alpha )=0$，$l_2 (\alpha )=2$，$l_3 (\alpha )=l_4 (\alpha )=0$和$l_1 (\beta )=2$、$l_2 (\beta )=0$，所以$\vert X(\alpha ,\beta )\vert =2^2=4$；当$\alpha =(\underline{} )(\underline{} )(\underline{} \underline{} )$和$\beta =(\underline{} )(\underline{} )$时，$l_1 (\alpha )=2$，$l_2 (\alpha )=1$，$l_3 (\alpha )=l_4 (\alpha )=0$和$l_1 (\beta )=2$，$l_2 (\beta )=0$，所以$\vert X(\alpha ,\beta )\vert =2^2 \times 2^1=8$；当$\alpha =(\underline{} \underline{} \underline{} \underline{} )$和$\beta =(\underline{} )(\underline{} )$时，$l_1 (\alpha )=l_2 (\alpha )=l_3 (\alpha )=0$，$l_4 (\alpha )=1$和$l_1 (\beta )=2$，$l_2 (\beta )=0$，所以$\vert X(\alpha ,\beta )\vert =2^1=2$.类似地，当$\alpha =(\underline{} )(\underline{} )(\underline{} )(\underline{} )$和$\beta =(\underline{} \underline{} )$时，$\vert X(\alpha ,\beta )\vert =0$；当$\alpha =(\underline{} \underline{} )(\underline{} \underline{} )$和$\beta =(\underline{} \underline{} )$时，$l_1 (\alpha )=0$时$\vert X(\alpha ,\beta )\vert =2^2=4$；当$\alpha =(\underline{} )(\underline{} )(\underline{} \underline{} )$和$\beta =(\underline{} \underline{} )$时$\vert X(\alpha ,\beta )\vert =0$；当$\alpha =(\underline{} \underline{} \underline{} \underline{} )$和$\beta =(\underline{} \underline{} )$时，$\vert X(\alpha ,\beta )\vert =2^1=2$.把所有项加起来再除以$\vert G\vert \vert H\vert $，便是轨的个数，等于

$$(16+3\times 4+2\times 8+2\times 2+0+3\times 4+2\times 0+2\times 2)/(8\times 2)=4,$$

即是说只用设计$4$个开关电路（图$4.16$）.

读者愿意试计算三个输入和一个输出的情况吗？