从化学的角度看，烷烃的计数问题应该较烷基的计数问题来得容易，因为烷基是从烷烃中取代一个氢原子得来的.但从数学的角度看，却刚好相反！由于烷基有一个碳原子连着基，地位较别的碳原子特殊，提供了一个让人“乘虚而入”的计算出发点.用树图的语言，就是有根树的计数问题比一般树的计数问题较易处理.为了暂时恢复这一点方便，让我们人为地选定一个点作根，先数数有多少个“有一个标了号的碳原子的烷烃”.设$P_m$是这种烷烃$Cm H{2m+2}$的个数（图$5.8$），$P(x)=p_1 x+p_2 x^2 +p_3 x^3 +\cdots $是这个计数问题的母函数.

从图中读者可以看到，那相当于数数在四个角上有多少个放置烷基的方法，这些烷基是容许在四个角上互相调换位置.因此，应该考虑的群是四次对称群$S_4$，它的圈指标是$(x_1^4 +6x_1^2 x_2 +3x_2^2 +8x_1 x_3 +6x_4 )/24$；$R$是全部烷基组成的集，权是碳原子的个数，权分布的母函数是上一节计算了的$A(x)$，这包括了$A_0 =1$（严格说来，那当然不算是一个烷基，只是一个氢原子）.根据波利亚计数定理，有

$$P(x)=xZ_G (A(x),A(x^2),A(x^3),A(x^4)) ,G=S_4 ,$$

也就是说

$$P(x)=x[A(x)^4+6A(x)^2A(x^2)+3A(x^2)^2+8A(x)\cdot A(x^3)+6A(x^4)]/24.$$

其次，我们再数数有多少个“有一个标了号的碳原子价键的烷烃”.设$Q_m $是这种烷烃$Cm H{2m+2}$的个数（图$5.9$），$Q(x)=Q_1 x+Q_2 x^2 +Q_3 x^3 +\cdots $是这个计数问题的母函数.

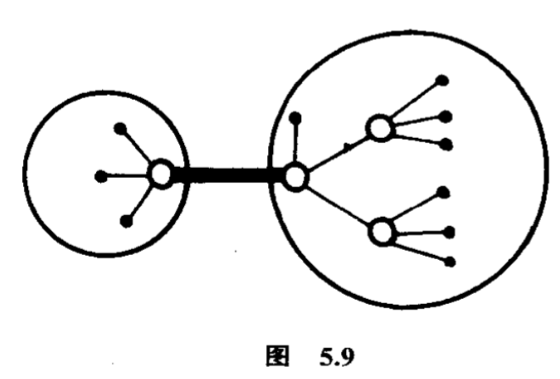
从图中读者可以看到，那相当于数数在两个位置上有多少个放置烷基的方法，这些烷基是容许在两个位置上作对换.因此，应该考虑是群是二次对称群$S_2 $，它的圈指标是$(x_1^2 +x_2 )/2$；$R$是全部烷基组成的集，权是碳原子的个数.权分布的母函数是$A(x)-1$，这儿我们不包括$A_0 =1$，是因为那个标了号的价键必须是连着两个碳原子的.根据波利亚计数定理，有

$$Q(x)=Z_G (A(x)-1,A(x^2)-1),G=S_2 ,$$

也就是说

$$\begin{align}
Q(x) & =\lbrace [A(x)-1]^2+[A(x^2)-1]\rbrace /2 \\
& =[A(x)^2+A(x^2)]/2-A(x).
\end{align}$$

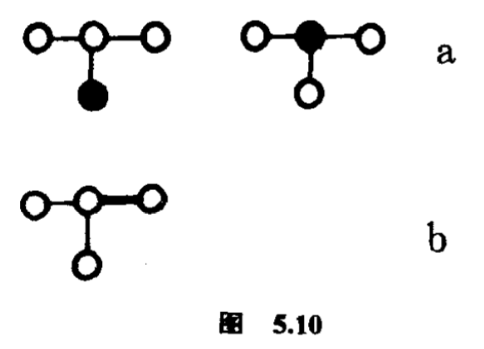
非常巧妙的一步，是英国数学家瑞德（R.C.Read）在$1972$年提出的.利用这个思想，他还计算了很多别的化学化合物的同分异构体的个数，有兴趣的读者可以参阅：R.C.Read.The enumeration of acyclic chemical compounds,in”Chemical applications of graph theory”,A.T.Balaban(ed.).New York:Academic Press,$1976\colon 25-61$.怎样糅合$P(x)$和$Q(x)$去计算不作任何标号的烷烃同分异构体的个数呢？瑞德提出这样的看法：给定了某个烷烃的同分异构体，把它的一个碳原子标号，有多少种不同的方法？比方丁烷$C4 H{10}$的一个同分异构体是三个碳原子分别连着第四个碳原子.把一个碳原子标号，有两种不同的方法（图$5.10(a)$）；把其中一个碳原子价键标号，只有一种方法（图$5.10(b)$）.

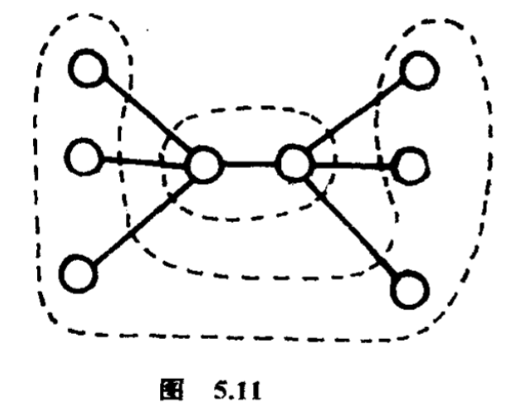
让我们又采用树图的观点考虑，$T$是一株$N$点树，把$T$的点标上$1$、$2$、$\cdots $、$N$.有些$\lbrace 1$、$2$、$\cdots $、$N\rbrace $的置换并不保持点的邻接关系，有些却仍然保持点的邻接关系，后者叫做$T$的自同构.一个$T$的自同构$\sigma $是个$\lbrace 1$、$2$、$\cdots $、$N\rbrace $的置换，如果点$v_1 $和$v_2 $有边相连，则点$\sigma (v_1 )$和$\sigma (v_2 )$也有边相连，反之亦然.直觉上的意思，$\sigma $只调换那些邻接性质相同的点，例如在下面的树里（图$5.11$），两边六个点可以互相调换，中间两个点也可以互相调换，但两边的六个点却不能跟中间的两个点调换.

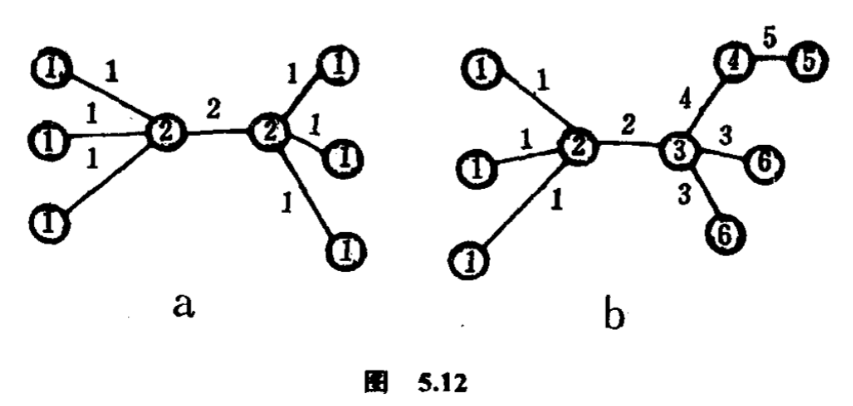
$T$的全部自同构组成一个群，叫做$T$的群，记作$G(T)$.对$G(T)$中元$\sigma $和$T$中点$v$，规定$\sigma \ast v =\sigma (v)$，这定义了群$G(T)$在树$T$上的一个作用，它的轨代表了一个其中一点给标了号的树.设$p$是轨的个数，它就是把$T$的一个点标号后得来的有根树的个数.$G(T)$也作用在$T$的边集上，如果$E$是相连$v_1 $和$v_2 $的边，$\sigma \ast E$就是相连$\sigma (v_1 )$和$\sigma (v_2 )$的边.这个作用下的轨代表了一个其中一条边给标了号的树.设$q$是轨的个数，它就是把$T$的一条边标号后得来的树的个数.$p$和$q$有没有关系呢？看看下面的例子（图$5.12(a)$），同一个轨的点以同一个数字表示，写在代表点的圆圈里；同一个轨的边也以同一个数字表示，写在边上面.在这个例子里，$p=2$和$q=2$.再看另一个例子（图$5.12(b)$），$p=6$和$q=5$.

前一个例子有个特点，就是树里有条“对称边”，意思是说这条边在某个$\sigma $的作用下不变更，当然，它连着两个落在同一个轨的点.说它是“对称点”，是因为它的两个端点必定各自连着结构相同的树.懂一点图论的读者，便知道一株树只有一个或者两个互相邻接的中心点，所谓中心点，就是指从那一点到别的点的最远距离（距离的计算是用点到点的段落个数）是最小，下面的树（图$5.13$）的中心点涂了黑色，每点旁边写上从那点至别的点的最远距离.

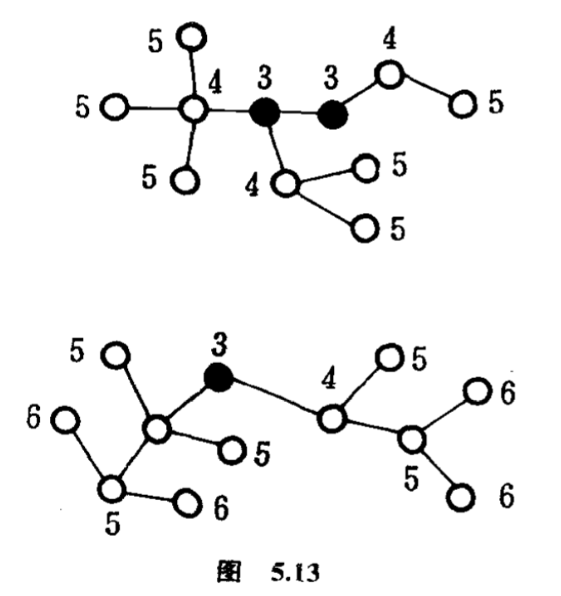
如果树只有一个中心点，它没有对称边；如果树有两个邻接的中心点但它们不落在同一个轨，它也没有对称边；只有当树有两个邻接的中心点而且它们落在同个轨，它才有对称边.一株树或者没有对称边或才只有一条对称边.在前一种情况，可以从树的每个轨找一个点，这些点有边连着，组成一株树，数数点和边的个数可知$p=q+1$（图$5.14(a)$）.在后一种情况，两个中心点各连着一株相同结构的树（图$5.14(b)$），每株树有$p$个轨的点和$(q-1)$个轨的边，由于$p=(q-1)+1$，便知道$p=q$.

于是，$p-q+s=1$，$s$是对称边的个数，且只能是$1$或$0$.现在，走遍每个点次数不大于$4$的$N$点树，有$\sum p-\sum q+\sum s=\sum 1=C_N$，$C_N$就是这种$N$点树的个数，也就是烷烃$CN H{2N+2}$的同分异构体的个数.右边就是$P_N -Q_N +\sum s$，$P_N $和$QN $在本节刚开首时已经提过了.要计算$\sum s$并不难，它是有一条对称边而且每点次数不大于$4$的$N$点树的个数.如果一株树有对称边，这条边连着两株相同结构的树，所以这种树的点数$N$必定是偶数，而且这种树的个数是$A{N/2}$，这儿的$A_m $是上一节出现过的母函数$A(x)$里$x^m $的系数.因此，当$N$是奇数时，$P_N -Q_N =C_N $；当$N$是偶数时，$P_N -QN +A{N/2} =C_N $.置$C(x)=C_1 +C_2 x^2 +\cdots $，便得到$C(x)=P(x)-Q(x)+A(x^2)-1$.我们在本节刚开首时已经计算了$P(x)$和$Q(x)$，它们都能通过$A(x)$表达.如果知道了$A(x)$，便可以知道$C(x)$，也就知道$C_1 $、$C_2 $、$\cdots $的数值了，下面是$N$从$1$到$20$的$C_N$的数值：

$$\begin{array}{cc}
N & C_N \\
\hline
1 & 1 \\
2 & 1 \\
3 & 1 \\
4 & 2 \\
5 & 3 \\
6 & 5 \\
7 & 9 \\
8 & 18 \\
9 & 35 \\
10 & 75 \\
\end{array} \quad
\begin{array}{cc}
N & C_N \\
\hline
11 & 159 \\
12 & 355 \\
13 & 802 \\
14 & 1\;858 \\
15 & 4\;347 \\
16 & 10\;359 \\
17 & 24\;894 \\
18 & 60\;523 \\
19 & 148\;284 \\
20 & 366\;319 \\
\end{array}$$

$C_N$也就是烷烃$CN H{2N+2}$的同分异构体个数，例如甲烷、乙烷和丙烷各只有一个，但丁烷有两个，戍烷有三个等等.波利亚也计算了当$N$无限增大时$C_N$的渐近公式，是$C_N \sim c^{-N} N^{-5/2} $，$c$是常数.

上面的计算只考虑同分异构体，关心的只是原子之间的键合，并没有顾及它们在空间的位置.原子在空间的位置对化合物的化学性质是会产生影响的，这个称作立体同分异构的现象，是法国科学家巴斯德（L.Pasteur）在$1848$年发现的，范霍夫在$1874$年开启了立体化学的研究.立体同分异构体的计数问题，基本上采用同样的方法，差别只在于考虑不同的群，瑞德在这方面做了不少计算，这儿就不介绍了，有兴趣的读者可以参阅刚才提过的文章，或者自己试一试.例如烷烃$CN H{2N+2}$的立体同分异构体个数$D_N$如下所示，$N$从$1$到$20\colon $

$$\begin{array}{cc}
N & D_N \\
\hline
1 & 1 \\
2 & 1 \\
3 & 1 \\
4 & 2 \\
5 & 3 \\
6 & 5 \\
7 & 11 \\
8 & 24 \\
9 & 55 \\
10 & 136 \\
\end{array} \quad
\begin{array}{cc}
N & D_N \\
\hline
11 & 345 \\
12 & 900 \\
13 & 2\;412 \\
14 & 6\;563 \\
15 & 18\;127 \\
16 & 50\;699 \\
17 & 143\;255 \\
18 & 408\;429 \\
19 & 1\;173\;770 \\
20 & 3\;396\;844 \\
\end{array}$$

这段故事，是数学和化学的一个优美的结合呀！