集合的概念

从$19$世纪末到$20$世纪初，集合论语言成为最通用的数学语言.这甚至表现在对数学所下的一种定义中，它说：数学就是研究集合上各种结构（关系）的科学.

“所谓集合，是我们直观感到或意识到的，由确定的、彼此不同的对象联合成的整体”；集合论的奠基人乔治$\cdot $康托尔就是这样描述集合概念的.

康托尔$(\mathrm{G.Cantor} )(1845-1918)$—德国数学家，无穷集理论的创始人，在数学中使用集合论语言的鼻祖.

康托尔的描述，当然不能叫做定义，因为它诉诸于可能比集合概念本身更复杂且从未定义过的概念.这种描述的目的是把这个概念与其他概念联系起来加以说明.

康托尔的（或叫做“朴素的”）集合论的基本前提可归结为：

$1^{\circ }$集合可由任意不同的事物组成；

$2^{\circ }$集合由构成它的事物集聚而唯一确定；

$3^{\circ }$任何性质都定义一个具有该性质的事物的集合.

若$x$是一事物，$P$是一性质，$P(x)$表示$x$有性质$P$.用$\lbrace x\vert P(x)\rbrace $表示具有性质$P$的一切事物的类.组成类或集合的事物，叫做类或集合的元素.

由元素$x_1 ,\cdots ,x_n $组成的集合用$\lbrace x_1 ,\cdots ,x_n \rbrace $表示.当不致引起混淆时，为了书写简单，我们直接用$a$表示单元素集合$\lbrace a\rbrace $.

“类”，“族”，“集体”，“组”等字，在朴素集合论中作“集合”的同义词来使用.

下面的例子说明这些术语的应用：

在词“ᴙ”中的字母“$a$”的集合；

阿达马的妻子的集合；

十个数码所成的组；

豆科植物族；

地球上沙粒的集合；

平面上与其上二已知点等距离的点的全体；

集合的族；

所有集合的集合.

集合课题的确定性在程度上可能具有的差别，向我们提示，集合这个概念，可不是那么简单和不出麻烦的概念.

事实上，例如一切集合的集合这个概念，就会产生矛盾.

$\blacktriangleleft $设$M$为一集合，用$P(M)$表示“$M$是不以自己作为元素的集”这样一种性质.

考察具有性质$P$的集合的类$K=\lbrace M\vert P(M)\rbrace $.

如果$K$是集合，那么，或者$P(K)$为真，或者$\neg P(K)$为真.然而，二者择一对于$K$是不可能的.实际上，$P(K)$不成立，因为由$K$的定义推知$K$包含着$K$，即$\neg P(K)$为真；另一方面，$\neg P(K)$也不可能真，因为这就表示$K$包含着$K$，而这与$K$的定义，亦即，它是不含自身的那样的集的类，相矛盾.

因此，$K$不是集合$\blacktriangleright $

这是经典的罗素悖论，它是朴素集合论所导致的悖论之一.

罗素$(\mathrm{B.Russell} )(1872-1970)$—英国逻辑学家，哲学家，社会学者，社会活动家.

在近代数理逻辑中，集合的概念受到了精细的推敲（我们会看到，这并不是无根据的）.但是，我们不去进行这种深入的分析.我们仅指出，在现行的公理化理论中，集合被定义为有一套确定性质的数学对象.

描述这些性质构成了公理.集合论公理系统的核心是假定了一些规则，根据这些规则可以从一些集合构成新的集合.总之，现行的任何公理体系，一方面，要避免朴素理论中众所周知的矛盾，另一方面，要保证适应于各种具体的集合，这些集合来源于数学的不同部门，首先是数学分析，当然是按广义理解下的数学分析.

我们对集合的概念，暂时就给出这些注释，并转而描述在分析中最常用的集合性质.

希望对集合概念作更详细地了解的读者，可参看本章$\S 4$的第二段，或查阅专门文献.

包含关系

已经说过，组成集合的事物，叫做该集合的元素.我们尽量地用大写拉丁字母表示集合，而用对应的小写字母表示集合的元素.

命题“$x$是集合$X$的元素”用符号简单地记作

$$x\in X(或X\ni x),$$

它的否命题用符号

$$x\notin X(或X\not\ni x)$$

来记.

在书写有关集合的命题时，经常运用逻辑运算$\exists $（“存在”或“找到”）与$\forall $（“任何的”或“对于任何的”），分别称之为存在量词与全称量词.

例如写法$\forall x((x\in A)\Leftrightarrow (x\in B))$表示的是，对于任何事物$x$，关系$x\in A$与$x\in B$是等价的.因为一个集合完全被它的元素所确定，所以，上述命题可以简记为

$$A=B,$$

读作“$A$等于$B$”，它表示集合$A$与集合$B$完全一致.

这样，当二集合由同样的元素构成时，它们相等.

否定相等就写成$A\neq B$.

若集合$A$的任何元素都是集合$B$的元素，就记作$A\subset B$或$B\supset A$，并说，集合$A$是集合$B$的子集，或说$B$包含$A$，或说$B$把$A$包含于自己内.因此，集合$A,B$间的关系$A\subset B$叫做包含关系（图$1$）.

于是，

$$(A\subset B)\colon =\forall x((x\in A)\Rightarrow (x\in B)).$$

如果$A\subset B$且$A\neq B$，就说包含关系$A\subset B$是严格的，或说$A$是$B$的真子集.利用所引进的定义，可推知

$$(A=B)\Leftrightarrow (A\subset B)\land (B\subset A).$$

如果$M$是集合，$P$是任一性质，那么，就能从$M$中分出一个子集

$$\lbrace x\in M\vert P(x)\rbrace ,$$

它是由$M$中具有这一性质的一切元素组成的子集.

例如，显然有

$$M=\lbrace x\in M \vert x\in M \rbrace .$$

另一方面，如果$P$是$M$中任何元素都不具有的一个性质，比如说，$P(x)\colon =(x\neq x)$，则我们得到集合

$$\varnothing =\lbrace x\in M\vert x\neq x\rbrace ,$$

它叫做$M$的空子集.

最简单的集合运算

设$A$与$B$都是集合$M$的子集.

$a$.集合

$$A\cup B\colon =\lbrace x\in M\vert (x\in A)\lor (x\in B)\rbrace ,$$

由$M$中的那些元素组成，它至少属于$A,B$中之一（图$2$），称此集为$A,B$的并集.

$b$.集合

$$A\cap B \colon =\lbrace x\in M\vert (x\in A)\lor (x\in B)\rbrace ,$$

由$M$中那些元素组成，它同时属于$A$和$B$（图$3$），称此集为$A,B$的交集.

$c$.集合

$$A\setminus B\colon =\lbrace x\in M\vert (x\in A)\land (x\notin B)\rbrace ,$$

由$M$中那些元素组成，它属于$A$但不属于$B$（图$4$），称此集为$A$，$B$的差集.

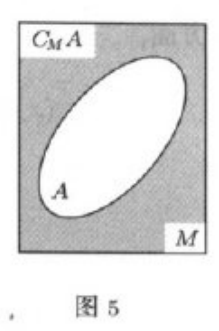
集$M$与$M$的子集$A$之差通常叫做$A$在$M$中的补集，记作$C_M A$，如果前后文能明显地知道$A$是哪个集中的补集时，就记作$CA$（图$5$）.

例$\quad $为了说明引进的这些概念的相互作用，我们验证下面的关系式（称之为德$\cdot $摩根规则）：

德$\cdot $摩根$(\mathrm{De.Morgan} )(1806-1871)$—英格兰数学家.

$$C_M (A\cup B)=C_M A \cap C_M B,\label{1} \tag{1}$$

$$C_M (A\cap B)=C_M A\cup C_M B.\label{2} \tag{2}$$

$\blacktriangleleft $例如我们来证明第一个等式：

$$\begin{align}
(x\in C_M (A\cup B)) & \Rightarrow (x\notin A\cup B) \\
& \Rightarrow ((x\notin A)\land (x\notin B)) \\
& \Rightarrow (x\in C_M A)\land (x\in C_M B) \\
& \Rightarrow (x\in (C_M A\cap C_M B)).
\end{align}$$

因此，得到

$$C_M (A\cup B)\subset (C_M A\cap C_M B).\label{3} \tag{3} $$

另一方面，

$$\begin{align}
(x\in (C_M A\cap C_M B)) & \Rightarrow ((x\in C_M A)\land (x\in C_M B)) \\
& \Rightarrow ((x\notin A)\land (x\notin B)) \\
& \Rightarrow (x\notin (A\cup B)) \\
& \Rightarrow (x\in C_M (A\cup B)) ,
\end{align}$$

即

$$C_M (A\cup B)\supset (C_M A\cap C_M B).\label{4} \tag{4} $$

由$\eqref{3}$与$\eqref{4}$即得到$\eqref{1}$.$\blacktriangleright $

$d$.集合的直积（笛卡儿积）.对于任意两个集合$A,B$，可构造出新的集合——对$\lbrace A,B\rbrace =\lbrace B,A\rbrace $，它的元素只有集合$A$和$B$.如果$A\neq B$，它有两个元素，而当$A=B$时，它只有一个元素.

这个新集合叫做$A$，$B$的无序对，以区别于序对$(A,B)$.在序对$(A,B)$中，元素$A,B$被赋予一种附加的特征，根据它分辨对$\lbrace A,B\rbrace $中的第一个元素和第二个元素.按定义，序对等式

$$(A,B)=(C,D),$$

表示$A=C$且$B=D$.特别地，如果$A\neq B$，那么$(A,B)\neq (B,A)$.

现设$X,Y$是任意两个集.按定义，由一切序对$(x,y)$（其第一项是$X$中的元素，而第$2$项是$Y$中的元素）所构成的集合

$$X\times Y\colon =\lbrace (x,y)\vert (x\in X)\land (y\in Y)\rbrace ,$$

叫做集合$X,Y$（按这样的次序！）的直积或笛卡儿积.

由直积的定义及上面关于序对所做的注释，一般来说，$X\times Y\neq Y\times X$.只有当$X=Y$时，等式才成立.这时我们把$X\times X$简记作$X^2 $.

直积又叫做笛卡儿积，以纪念笛卡儿，他曾与费马各自独立地通过坐标系引进了几何的分析语言.众所周知的平面笛卡儿坐标系，恰好把平面变成了两个数轴的直积.笛卡儿与它的因子的次序有关这一点，在这个熟知的情形是非常显然的.例如，序对$(0,1)$和$(1,0)$对应于平面上两个不同的点.

笛卡儿$(\mathrm{Descartes} )(1596-1650)$—著名的法国哲学家，数学家与物理学家.他在科学思想法和认识论方面作出了重大贡献.

费马$(\mathrm{Fermat} )(1601-1665)$—卓越的法国数学家，职业法学家.费马在分析，解析几何，概率论，数论等一系列现代数学领域中，都居于创始的地位.

设序对$z=(x_1 ,x_2 )$是集合$X_1 ,X_2 $的直积$X_1 \times X_2 $中的元素，$x_1 $叫做序对$z$的第一射影，记作$\mathrm{pr_1 }z$；而$x_2 $叫做序对$z$的第二射影，记作$\mathrm{pr_2 } z$.

练习

在问题$1,2,3$中用$A,B,C$表示某集$M$的子集.

$1$.验证下面诸关系式：

$(a)\quad (A\subset C)\land (B\subset C)\Leftrightarrow ((A\cup B)\subset C)$；

$(b)\quad (C\subset A)\land (C\subset B)\Leftrightarrow (C\subset (A\cap B))$；

$(c)\quad C_M (C_M A)=A$；

$(d)\quad (A\subset C_M B)\Leftrightarrow (B\subset C_M A)$；

$(e)\quad (A\subset B)\Leftrightarrow (C_M A\supset C_M B)$.

证$\quad (a)$先证$(A\subset C)\land (B\subset C)\Rightarrow ((A\cup B)\subset C)$.任取$x,y$，$x\in A$，$y\in B$，$x\in A\land y\in B\Rightarrow x\in C\land y\in C\Rightarrow x,y\in C$，从而得到$((A\cup B)\subset C)$.

再证$((A\cup B)\subset C)\Rightarrow (A\subset C)\land (B\subset C)$.这可以由$A\subset (A\cup B)\subset C$，$B\subset (A\cup B)\subset C$得到.

故成立$(a)(A\subset C)\land (B\subset C)\Leftrightarrow ((A\cup B)\subset C)$.

$(b)$先证$(C\subset A)\land (C\subset B)\Rightarrow (C\subset (A\cap B))$.任取$x$，$x\in C\Rightarrow x\in C\land x\in C\Rightarrow x\in A\land x\in B\Rightarrow x\in A\cap B$，从而得到$(C\subset (A\cap B))$.

再证$(C\subset (A\cap B))\Rightarrow (C\subset A)\land (C\subset B)$.这可以由$C\subset A\cap B\subset A$，$C\subset A\cap B\subset B$得到.

故成立$(C\subset A)\land (C\subset B)\Leftrightarrow (C\subset (A\cap B))$.

$(c)$由于$x\in C_M (C_M A)\Rightarrow x\notin C_M A\Rightarrow x\in A$.因此，得到$C_M (C_M A)\subset A$.

另一方面，$x\in A\Rightarrow x\notin C_M A\Rightarrow x\in C_M (C_M A) $.即$C_M (C_M A)\supset A$.

故$C_M (C_M A)=A$.

$(d)$先证$(A\subset C_M B)\Rightarrow (B\subset C_M A)$.任取$x$，$x\in A\Rightarrow x\in C_M B\Rightarrow x\notin B$，故$A\cap B=\varnothing $.于是，任取$y$，$y\in B\Rightarrow y\notin A\Rightarrow y\in C_M A$，从而得到$(B\subset C_M A)$.

同理可证$(B\subset C_M A)\Rightarrow (A\subset C_M B)$.综上所述，$(A\subset C_M B)\Leftrightarrow (B\subset C_M A)$.

$(e)$根据$(d)$式结论，用$C_M B$代替$(d)$式子里的$B$，得$(A\subset C_M (C_M B))\Leftrightarrow ((C_M B)\subset C_M A)$成立.根据$(c)$式，知$C_M (C_M B)=B$，代入上式，得到$(A\subset B)\Leftrightarrow ((C_M B)\subset C_M A)$成立，该式等价于$(A\subset B)\Leftrightarrow (C_M A\supset C_M B)$.

$2$.试证

$(a)\quad A\cup (B\cup C)=(A\cup B)\cup C=\colon A\cup B\cup C$；

$(b)\quad A\cap (B\cap C)=(A\cap B)\cap C=\colon A\cap B\cap C$；

$(c)\quad A\cap (B\cup C)=(A\cap B)\cup (A\cap C)$；

$(d)\quad A\cup (B\cap C)=(A\cup B)\cap (A\cup C)$.

证$\quad (a)$根据定义，成立

$$B\cup C\colon =\lbrace x\in M\vert (x\in B)\lor (x\in C)\rbrace ,$$

$$A\cup B\colon =\lbrace x\in M\vert (x\in A)\lor (x\in B)\rbrace .$$

因此，有以下两式成立

$$A\cup (B\cup C)\colon =\lbrace x\in M\vert (x\in A)\lor (x\in B)\lor (x\in C)\rbrace ,$$

$$(A\cup B)\cup C\colon =\lbrace x\in M\vert (x\in A)\lor (x\in B)\lor (x\in C)\rbrace .$$

另一方面，根据定义，又有

$$A\cup B\cup C\colon =\lbrace x\in M\vert (x\in A)\lor (x\in B)\lor (x\in C)\rbrace ,$$

结合上面三式，可得$A\cup (B\cup C)=(A\cup B)\cup C=\colon A\cup B\cup C$.

$(b)$根据定义，成立

$$B\cap C\colon =\lbrace x\in M\vert (x\in B)\land (x\in C)\rbrace ,$$

$$A\cap B\colon =\lbrace x\in M\vert (x\in A)\land (x\in B)\rbrace .$$

因此，有以下两式成立

$$A\cap (B\cap C)\colon =\lbrace x\in M\vert (x\in A)\land (x\in B)\land (x\in C)\rbrace ,$$

$$(A\cap B)\cap C\colon =\lbrace x\in M\vert (x\in A)\land (x\in B)\land (x\in C)\rbrace .$$

另一方面，根据定义，又有

$$A\cap B\cap C\colon =\lbrace x\in M\vert (x\in A)\land (x\in B)\land (x\in C)\rbrace ,$$

结合上面三式，可得$A\cap (B\cap C)=(A\cap B)\cap C=\colon A\cap B\cap C$.

$(c)$我们将通过说明等式的每一边是另一边的子集来证明这个恒等式.

假定$x\in A\cap (B\cup C)$，那么$x\in A$且$x\in (B\cup C)$.根据集合并的定义，可得$x\in A$且$x\in B$或$x\in C$；因此，$x\in A$且$x\in B$或$x\in A$且$x\in C$.根据交的定义，可知$x\in A\cap B$或$x\in A\cap C$；使用并的定义，可得$x\in (A\cap B)\cup (A\cap C)$；由此$A\cap (B\cup C)\subset (A\cap B)\cup (A\cap C)$.

现在假定$x\in (A\cap B)\cup (A\cap C)$，那么，由并的定义，$x\in A\cap B$或$x\in A\cap C$；由交的定义，可得$x\in A$且$x\in B$或$x\in A$且$x\in C$；由此可知，$x\in A$，$x\in B$或$x\in C$；因此，由并的定义可知，$x\in A$且$x\in B\cup C$.而且，由交的定义，可得$x\in A\cap (B\cup C)$；最终得出$(A\cap B)\cup (A\cap C)\subset A\cap (B\cup C)$.这便完成了恒等式的证明.

$(d)$我们将通过说明等式的每一边是另一边的子集来证明这个恒等式.

假定$x\in A\cup (B\cap C)$，那么$x\in A$或$x\in (B\cap C)$.根据集合交的定义，可得$x\in A$或$x\in B$且$x\in C$；因此，$x\in A$或$x\in B$且$x\in A$或$x\in C$.根据并的定义，可知$x\in A\cup B$且$x\in A\cup C$；使用交的定义，可得$x\in (A\cup B)\cap (A\cup C)$；由此$A\cup (B\cap C)\subset (A\cup B)\cap (A\cup C)$.

现在假定$x\in (A\cup B)\cap (A\cup C)$，那么，由交的定义，$x\in A\cup B$且$x\in A\cup C$；由并的定义，可得$x\in A$或$x\in B$且$x\in A$或$x\in C$；由此可知，$x\in A$或$x\in B$且$x\in C$；因此，由交的定义可知，$x\in A$或$x\in B\cap C$.而且，由并的定义，可得$x\in A\cup (B\cap C)$；最终得出$(A\cup B)\cap (A\cup C)\subset A\cup (B\cap C)$.这便完成了恒等式的证明.

$3$.验证并与交运算的对偶关系：

$(a)\quad C_M (A\cup B)=C_M A\cap C_M B$；

$(b)\quad C_M (A\cap B)=C_M A\cup C_M B$.

证$\quad (a)$首先，

$$\begin{align}
(x\in C_M (A\cup B)) & \Rightarrow (x\notin A\cup B) \\
& \Rightarrow ((x\notin A)\land (x\notin B)) \\
& \Rightarrow (x\in C_M A)\land (x\in C_M B) \\
& \Rightarrow (x\in (C_M A\cap C_M B)).
\end{align}$$

因此，得到

$$C_M (A\cup B)\subset (C_M A\cap C_M B).$$

另一方面，

$$\begin{align}
(x\in (C_M A\cap C_M B)) & \Rightarrow ((x\in C_M A)\land (x\in C_M B)) \\
& \Rightarrow ((x\notin A)\land (x\notin B)) \\
& \Rightarrow (x\notin (A\cup B)) \\
& \Rightarrow (x\in C_M (A\cup B)) ,
\end{align}$$

即

$$C_M (A\cup B)\supset (C_M A\cap C_M B).$$

综上所述，得到$C_M (A\cup B)= (C_M A\cap C_M B)$.

$(b)$首先，

$$\begin{align}
(x\in C_M (A\cap B)) & \Rightarrow (x\notin A\cap B) \\
& \Rightarrow ((x\notin A)\lor (x\notin B)) \\
& \Rightarrow (x\in C_M A)\lor (x\in C_M B) \\
& \Rightarrow (x\in (C_M A\cup C_M B)).
\end{align}$$

因此，得到

$$C_M (A\cap B)\subset (C_M A\cup C_M B).$$

另一方面，

$$\begin{align}
(x\in (C_M A\cup C_M B)) & \Rightarrow ((x\in C_M A)\lor (x\in C_M B)) \\
& \Rightarrow ((x\notin A)\lor (x\notin B)) \\
& \Rightarrow (x\notin (A\cap B)) \\
& \Rightarrow (x\in C_M (A\cap B)) ,
\end{align}$$

即

$$C_M (A\cap B)\supset (C_M A\cup C_M B).$$

综上所述，得到$C_M (A\cap B)= (C_M A\cup C_M B)$.

$4$.对下列集合的笛卡儿积作出几何解释：

$(a)\quad $二线段（矩形）；

$(b)\quad $二直线（平面）；

$(c)\quad $直线与圆周（圆柱面）；

$(d)\quad $直线与圆面（圆柱体）；

$(e)\quad $二圆周（圆环面）；

$(f)\quad $圆周与圆面（实圆环）.

解$\quad (a)$设集合$X=\lbrace x\in M_1 \vert M_1 =[a,b]\rbrace $位于$x$轴，集合$Y=\lbrace y\in M_2 \vert M_1 =[c,d]\rbrace $位于$y$轴，则

$$X\times Y=\lbrace (x,y)\in M_1 \times M_2 \vert M_1 \times M_2 =[a,b]\times [c,d]\rbrace ,$$

即二线段的笛卡儿积作成一矩形.

$(b)$由$(a)$可知，当$a,b\to -\infty $，$c,d\to +\infty $时，即无限延长线段$M_1 $和$M_2 $时，二直线的笛卡儿积应作成一无边界的矩形，即平面.

$(c)$在空间直角坐标系中，取任一经过圆周$l_2 $边界的直线$l_1 $上的点$x$且$l_1 $与轴$Oz$平行，并取与底面$Oxy$平行且半径为$r$的圆周$l_2 $上的点$y $，满足$X=\lbrace x \in l_1 \vert l_1 \in (-\infty ,+\infty )\rbrace $且$Y=\lbrace y\in (c,d) \vert c^2 +d^2 =r^2 \rbrace $，则直线与圆周的直积

$$X\times Y=\lbrace (s,c,d)\in l_1 \times (c,d)\vert s\in l_1 ,c^2+d^2 =r^2 \rbrace $$

构成空间中的一个圆柱圆.

$(d)$在空间直角坐标系中，取任一经过圆周$l_2 $边界的直线$l_1 $上的点$x$且$l_1 $与轴$Oz$平行，并取与底面$Oxy$平行且半径为$r$的圆周$l_2 $内的点$y $，满足$X=\lbrace x \in l_1 \vert l_1 \in (-\infty ,+\infty )\rbrace $且$Y=\lbrace y\in (c,d) \vert c^2 +d^2 \leqslant r^2 \rbrace $，则直线与圆周的直积

$$X\times Y=\lbrace (s,c,d)\in l_1 \times (c,d)\vert s\in l_1 ,c^2+d^2 \leqslant r^2 \rbrace $$

构成空间中的一个圆柱体.

$(e)$根据拓扑学定义，一个圆沿着另一圆的圆周旋转一周，可知两个圆周的直积是圆环面.如图所示.

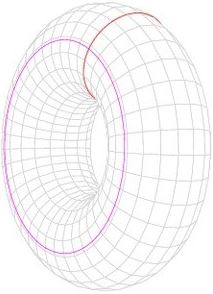
$(f)$根据$(e)$的说明，可知圆周与圆面的直积是一个实圆环.

$5$.集合$\Delta =\lbrace (x_1 ,x_2 )\in X^2 \vert x_1 =x_2 \rbrace $叫做集合$X$的笛卡儿正方形$X^2 $的对角线.对第$4$题的$a),b),e)$所得之集的对角线做出几何解释.

解$\quad (a)$如果矩形经过直线$y=x$，那么$(a)$所得之集的对角线的几何解释应是一线段$L=\lbrace (x,x)\in L\vert (x,x)\in X\times Y\rbrace $.

$(b)$所得之集的对角线从几何角度看，明显是一条直线$L$，其方程为$L\colon y=x$.

$(e)$所得之集的对角线从几何角度看应是一个椭圆面或两个圆面，是由第$4$题$(e)$所得之集即圆环面与在空间直角坐标系中垂直于底面$Oxy$的对角线的平面所成的截面.在空间直角坐标系中，随着圆环面的不同位置，所成的截面是不同的.

$6$.试证：

$(a)\quad (X\times Y=\varnothing )\Leftrightarrow (X=\varnothing )\lor (Y=\varnothing )$，

而如果$X\times Y\neq \varnothing $，则

$(b)\quad (A\times B\subset X\times Y)\Leftrightarrow (A\subset X)\land (B\subset Y)$.

$(c)\quad (X\times Y)\cup (Z\times Y)=(X\cup Z)\times Y$.

$(d)\quad (X\times Y)\cap (X’ \times Y’)=(X\cap X’ )\times (Y\cap Y’)$.

这里$\varnothing $表空集，即不包含任何元素的集合.

证$\quad (a)$先证$(X\times Y=\varnothing )\Rightarrow (X=\varnothing )\lor (Y=\varnothing )$，任取$x\in X$，$y\in Y$，$\langle x,y\rangle \in X\times Y$，这时$x\in X\land y\in Y $.由于$X\times Y=\varnothing $，故$x\in X=\varnothing $或$y\in Y=\varnothing $成立，即$\langle x,y\rangle \in (X=\varnothing )\lor (Y=\varnothing )$.

再证$(X=\varnothing )\lor (Y=\varnothing )\Rightarrow (X\times Y=\varnothing )$，明显的，由定义知，若$X$或$Y$之一有一个是空集，则$X$与$Y$的直积也是空集.

$(b)$先证$(A\times B\subset X\times Y)\Rightarrow (A\subset X)\land (B\subset Y)$.任取$a\in A,b\in B$，则

$$\begin{align}
& \langle a,b\rangle \in A\times B\Rightarrow \langle a,b\rangle \in X\times Y \\
\Rightarrow & a\in A\land b\in B \Rightarrow a\in X\land b\in Y \\
\Rightarrow & (a\in A\Rightarrow a\in X)\land (b\in B\Rightarrow b\in Y) \\
\Rightarrow & \langle a,b\rangle \in (A\subset X)\land (B\subset Y)
\end{align}$$

$(c)$任取$\langle x,y\rangle $，有

$$\begin{align}
& \langle x,y\rangle \in (X\cup Z)\times Y \\
\Leftrightarrow & x\in X\cup Z \land y\in Y \\
\Leftrightarrow & (x\in X\lor x\in Z )\land y\in Y \\
\Leftrightarrow & (x\in X\land y\in Y)\lor (x\in Z\land y\in Y) \\
\Leftrightarrow & \langle x,y\rangle \in X\times Y\lor \langle x,y\rangle \in Z \times Y \\
\Leftrightarrow & \langle x,y\rangle \in (X\times Y)\cup (Z \times Y)
\end{align}$$

$(d)$任取$\langle x,y\rangle $，有

$$\begin{align}
& \langle x,y\rangle \in (X\cap X’ )\times (Y\cap Y’) \\
\Leftrightarrow & x\in X\cap X’ \land y\in Y\cap Y’ \\
\Leftrightarrow & x\in X\land x\in X’ \land y\in Y\land y\in Y’ \\
\Leftrightarrow & (x\in X\land y\in Y)\land (x\in X’\land y\in Y’) \\
\Leftrightarrow & \langle x,y\rangle \in X\times Y\land \langle x,y\rangle \in X’ \times Y’ \\
\Leftrightarrow & \langle x,y\rangle \in (X\times Y)\cap (X’ \times Y’)
\end{align}$$

$7$.将问题$3$中的关系与$\S 1$练习$2$中的关系$a),b)$比较，建立对于命题的逻辑运算$\neg ,\land ,\lor $与对于集合的运算$C,\cap ,\cup $之间的关系.

解$\quad $由“且”$\land $的含义，我们可以用“且”$\land $来定义集合$A$和集合$B$的交集$\cap $

$$A\cap B=\lbrace x\vert (x\in A)\land (x\in B)\rbrace .$$

由“或”$\lor $的含义，我们可以用“或”$\lor $来定义集合$A$和集合$B$的并集$\cup $

$$A\cup B=\lbrace x\vert (x\in A)\lor (x\in B)\rbrace .$$

由“非”$\neg $的含义，我们可以用“非”$\neg $来定义集合$A$在全集$M$中的补集$C_M A$

$$C_M A=\lbrace x\in U\vert \neg (x\in A)\rbrace =\lbrace x\in U\vert x\notin A\rbrace .$$