公元元年以后，在亚历山大，数学研究还在继续着，但人们对这门学科本身的兴趣在逐渐减退，它逐渐成了其他学科尤其是天文学的辅助学科.这个时期的著名人物是托勒密（克罗狄$\cdot $托勒密），他于公元$2$世纪中叶享有盛名.托勒密是一位天文学家，他的伟大著作《大汇编》[$Syntaxis$，后来人们称为《至大论》（$Almagest$）]主要是天文学方面的论著.但是它在数学史中很重要，因为它可以说是三角学最早的系统性论著.有充分的理由相信，在《至大论》一书中，很多内容都是喜帕恰斯所知道的，而托勒密很可能也熟悉梅内克缪斯的《球面几何学》（$Spharica$），后者有相当篇幅讨论到球面三角形的性质.

三角学这门学科是从确定平面三角形和球面三角形的边和角的关系开始的.很可能埃及人早已发现三角形的不同元素之间具有某种关连，但首先看到有必要建立三角形的边与角之间的精确关系的乃是希腊人.托勒密在天文学上的研究要求建立某些能精确确定这些关系的规则，正是为了改善天文学计算，三角学才应运而生.因此，球面三角学的研究先于平面三角学.这些规则，有许多可在《至大论》一书的第一卷中找到.

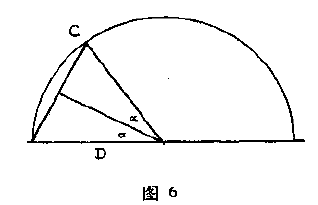
我们现时称为三角函数的那些比值，无论是托勒密还是当时的任何其他希腊人都没有使用过.他们只讲一个角的弦，他们的所谓弦，就是圆弧上对圆心角所张弧的长度.由于弧的大小是它所对之角的量度，所以很显然，在图$6$中弦$2\alpha $（即在弧上对着角$2\alpha $所张弦的长度）和我们所说的$\sin{\alpha } $之间存在的等价性；不难看出，$\dfrac{1}{2} \mathrm{chord} \;2\alpha $和$\sin{\alpha } $是两个等价表达式（图$6$）因此，当托勒密（或喜帕恰斯）着手建立以$(\dfrac{1}{2} )^{\circ} $为间隔的从$(\dfrac{1}{2} )^{\circ} $到$180^{\circ}$之间所有角度的弦数表时，所建立的其实是一个以$(\dfrac{1}{4} )^{\circ} $为间隔的$(\dfrac{1}{4} )^{\circ} $到$90^{\circ}$角的正弦表.

可以预料，托勒密的方法相当复杂，这是由于当时的知识条件所限制.但他所遵循的原理可以简述如下：

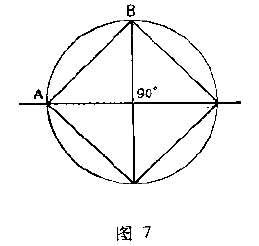
首先他认识到，确定不同角度的弦相当于如何设法解决用圆的直径长度表示圆内接正多边形的边长问题.承认了这点后，他就把圆周分成$360$等份，即$360$度.直径则被分成$120$等份，使用的完全是六十进位分法，并且事实上也推广到分数.对于这些等份，他使用了等份、分、称等名称.这样就能用直径上的许多等份来表示圆弧上对任一圆心角所张弦的长度.这就是角的弦.例如，如果有一圆内接六边形，它的边就是$60^{\circ}$角的弦.而这显然又等于半径，或直径上$120$等份中的$60$等份.这个结果与$\sin{30^{\circ}} =\dfrac{1}{2} $之间的等价性是一目了然的.其他角度的弦也可以用类似方法得到.例如，$\mathrm{chord} \;90^{\circ}$是直径被分成$120$等份的圆的内接正方形的边长，亦即$\mathrm{chord} \;90^{\circ} =AB=\sqrt{60^2+60^2} =84.852\;6$（图$7$）

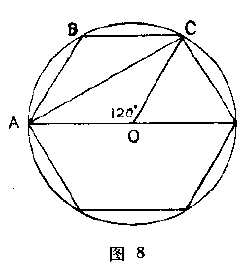
如改用六十进位制计算，它即为$84^p 51’10’’$.同样，$\mathrm{chord} \;120^{\circ} =AC$（图$8$）$=2\sqrt{60^2-30^2} =103.9224$

或是以六十进位制表示为$103^p 55’23’’$.在这些关系中，很容易看出$\sin{45^{\circ}}$和$\sin{60^{\circ}}$的值.

为了求得$\mathrm{chord} \;36^{\circ}$和$\mathrm{chord} \;72^{\circ}$，亦即圆内接正五边形和正十边形的边，托勒密依靠了欧几里得的帮助.以$AB$为直径，$O$为中心作一圆.作$OC$垂直于$AB$，并在$D$点平分$OB$.在$DA$上画出一段$DE$，使等于$DC$，并连接$EC$.（图$9$）

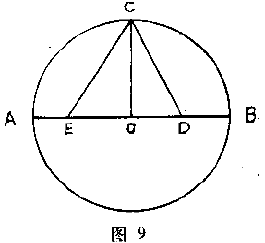
于是$OE$便是内接十边形的边，而$EC$则为内接五边形的边.因为，由于$BO$在$D$点被平分并延长到$E$，所以根据欧几里得第二卷，命题$6$，我们有

$$BE\cdot EO+OD^2 =DE^2=DC^2=OC^2+OD^2$$

因此$BE\cdot EO=OC^2$或$OB^2$

所以$BE$在$O$处被分成中末比.欧几里得曾证明（第十三卷，命题$9$）：“如把同一圆内的内接正六边形和正十边形的边重合在一起，则整条线段在分点处被分成中末比，其较小的一段是十边形的边.”因此，由于$BO$显然是圆内接正六边形的边，所以$EO$就是同样画出的正十边形的边.为了求出它的大小，可假定$a$是圆的半径.以$x$表示$EO$，则

$$BE\cdot EO=OB^2$$

即$(a+x)x=a^2$

因而$x=\dfrac{1}{2} a(\sqrt{5} -1)$

这就是半径为$a$的圆的内接正十边形的边.为了求出圆内接正五边形的边，托勒密依靠了欧几里得第十三卷中的命题$10$，这个命题指出：“如果有一正五边形内接于一圆，则此五边形边的平方，等于同一圆的内接六边形边的平方与内接十边形边的平方之和”.这样就确立了内接于同一圆内的五边形、六边形及十边形的边之间的关系.我们可以把这个关系写成：

$($五边形的边$)^2 =($六边形的边$)^2 +($十边形的边$)^2 =a^2+\dfrac{1}{4} a^2 (\sqrt{5} -1)^2$

因而所求的长度是$\dfrac{1}{2} a\sqrt{10-2\sqrt{5} } $，这里$a$是圆的半径.现在我们来求$\mathrm{chord} \;36^{\circ}$，它是$36^{\circ}$圆心角所对弦的长度.由上述我们得：

弦长$=$十边形的边$=\dfrac{1}{2} a(\sqrt{5} -1)=37.083$（由于$a=60$）$=37^p 4’55’’$

至于$\mathrm{chord} \;72^{\circ} $，我们有

弦长$=$五边形的边$=\dfrac{1}{2} a\sqrt{10-2\sqrt{5} }=70.536=70^p 32’3’’$

读者不难把这些关系分别与$\sin{18^{\circ}}$和$\sin{36^{\circ}}$的值联系起来.

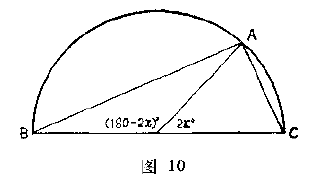
托勒密为了扩充他的表，不得不利用许多为任何初学三角学的人所熟知的关系.从图$10$显然可以看出

$(\mathrm{chord} \;2x^{\circ})^2 +\mathrm{chord} \;(180^{\circ} -2x^{\circ})^2=AC^2+AB^2=BC^2$，即$120^2 $

因为$\dfrac{1}{2} \mathrm{chord} \;2x^{\circ} $等于$\sin{x^{\circ}}$，而$\dfrac{1}{2} \mathrm{chord} \;(180^{\circ} -2x^{\circ}) $等于$\sin{(90^{\circ} -x^{\circ})} $或$\cos{x^{\circ}}$，所以上式也就是著名的关系：

$$\sin{}^2 \theta +\cos{}^2 \theta =1$$

因此要求$\mathrm{chord} \;108^{\circ}$时，我们有

$$(\mathrm{chord} \;108)^2 +(\mathrm{chord} \;72)^2 =120^2$$

或

或$(\mathrm{chord} \; 108^{\circ})^2 =120^{\circ} -(70.536)^2$

因而$\mathrm{chord} \;108^{\circ} =97.080\;7$

这就是以直径$(=120)$来表示的$\mathrm{chord} \;108^{\circ} $.现在

$$\dfrac{1}{2} \mathrm{chord} \;108^{\circ} =\sin{54^{\circ}} $$

因此$\sin{54^{\circ}} $等于$48.540\;4$，如以半径$(=60)$的分数来表示，则为$0.809\;01$.

托勒密下一步是求$\mathrm{chord} \;(\alpha -\beta )$的表示式.这可以帮助他从已经确定了的$\mathrm{chord} \;72^{\circ} $和$\mathrm{chord} \;60^{\circ} $的值，求出$\mathrm{chord} \;12^{\circ} $的值来.他的方法如下：

在直径$AD$上作一半圆，$B$和$C$是半圆上的两点.（图$11$）

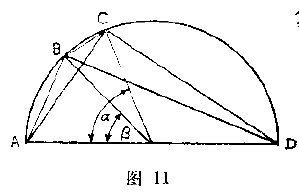
$\alpha $角和$\beta $角如图所示，显然，

$AC=\mathrm{chord} \;\alpha $

$AB=\mathrm{chord} \;\beta $

$BC=\mathrm{chord} \;(\alpha -\beta ) $

$BD=\mathrm{chord} \;(180^{\circ} -\beta ) $

$CD=\mathrm{chord} \;(180^{\circ} -\alpha ) $

从著名的定理：

$$AC\cdot BD=BC\cdot AD+AB\cdot CD,$$

或$BC\cdot AD=AC\cdot BD-AB\cdot CD$

可知

$$\begin{align}
& \lbrace \mathrm{chord} \;(\alpha -\beta ) \rbrace \cdot \lbrace \mathrm{chord} \;180^{\circ} \rbrace \\
= & (\mathrm{chord} \;\alpha )\cdot \lbrace \mathrm{chord} \;(180^{\circ} -\beta ) \rbrace -(\mathrm{chord} \;\beta )\cdot \lbrace \mathrm{chord} \;(180^{\circ} -\alpha ) \rbrace
\end{align}$$

当然，这无非是$\sin{(A-B)}$的公式.

为了扩充他的表，托勒密还不得不去确立半角的弦和全角的弦之间的关系，这个关系在今天应以下一公式表示：

$$\sin{}^2 \theta =\dfrac{1}{2} (1-\cos{2\theta }) .$$

以$AB$为直径、$O$为圆心作一圆，画出两相等的弦$CB$，$AD$.称$\triangle AOD=\triangle BOC=\dfrac{1}{2} \theta $，则有

$$AD\cdot CB+CD\cdot AB=AC\cdot BD$$

亦即$AD^2+CD\cdot AB=BD^2=AB^2 -AD^2 $

因此$2AD^2 =AB^2-AB\cdot CD$

$$AD^2=\dfrac{1}{2} AB(AB-CD) $$

或

$$(\mathrm{chord} \;\dfrac{1}{2} \theta )^2 =\dfrac{1}{2} (\mathrm{chord} \;180^{\circ}) \lbrace \mathrm{chord} \;180^{\circ} -\mathrm{chord} \;(180^{\circ} -\theta )\rbrace $$

托勒密从$\mathrm{chord} \;120^{\circ}$的已知值，用这个公式求出了$\mathrm{chord} \;30^{\circ}$，$\mathrm{chord} \;15^{\circ}$，$\mathrm{chord} \;7.5^{\circ}$等.同样，已知$\mathrm{chord} \;90^{\circ}$的值就能算出$\mathrm{chord} \;45^{\circ}$，$\mathrm{chord} \;22.5^{\circ}$，$\mathrm{chord} \;11.25^{\circ}$等的值.托勒密重复应用这个公式，造了一个弦数表，以$30’$为间隔，一直计算到$\mathrm{chord} \;1.5^{\circ}$和$\mathrm{chord} \;0.75^{\circ}$，他求出$\mathrm{chord} \;1.5^{\circ}$是$1^{p} 34’15’’$，$\mathrm{chord} \;0.75^{\circ}$是$0^p 47’8’’$.在计算$\mathrm{chord} \;1^{\circ}$时，他利用了一个定理：若在同一圆中作两条不等弦，则大弦与小弦之比，小于大弦所对的弧与小弦所对的弧之比.也就是说，如果$AB$和$CD$是圆中的两个不等弦，则$AB\colon CD$小于$\stackrel \frown {AB} \colon \stackrel \frown {CD} $，这个不等式在今天应写为$\dfrac{\sin{\alpha } }{\sin{\beta } } < \dfrac{\alpha }{\beta } $.在此基础上，他利用内插法获得$\mathrm{chord} \;1^{\circ}$的值是$1^p 2’50’’$，并由此得出了$\mathrm{chord} \;(\dfrac{1}{2} )^{\circ}$即$\sin{(\dfrac{1}{4} )^{\circ }}$的值是$o^p 31’25’’$，它准确到小数点后第六位数.

在托勒密以后，人们对天文学的兴趣减退了，因此三角学的研究也趋衰微.直到公元$5$世纪才开始有了一点复兴迹象，这种迹象首先在东方出现.印度人在计算技巧方面总是显得很熟练，他们很快采用了亚历山大学派的天文学知识，从而恢复了对三角学这门基础科学的兴趣.和这次复兴有关的人物是包利萨、阿耶波多、婆罗摩笈等人，几世纪以后还有婆什迦罗.

印度人同希腊人一样，也把圆分成$360$度，或$21\;600$分，但他们并不像托勒密那样把直径分成$120$等份，而是由包利萨（公元$5$世纪初）把半径分成了$120$等份.在他以后，有一位卓越的天文数学家阿耶波多（$476-550$）曾采用另外一种度量半径的方法，他用这种方法能把角的正弦表示出来，有些像我们的弧度法那样.阿耶波多使圆周仍旧被分成$21\;600$等份，用同样单位来度量半径.他已经知道，圆周与直径之比是$3.141\;6\colon 1$，这意味着半径的长度为：

$$\dfrac{21\;600}{2\times 3.141\;6}$$

或$3\;438$

其单位与圆周被分成的等份相同.后来的一位数学家婆罗摩笈多把半径分成了$3\;270$等份，分成这个值的原因不详.

印度人使用了我们所称的正弦函数和正矢$(1-\cos{\theta } )$.但是必须指出，当时把正弦仍然看做长度，看做二倍角所对弧上张开的弦长的一半.这个长度是用和半径一样的单位来度量的，因而当他们写成$\sin{60^{\circ}}=2\;977$时，这是指一个二倍于$60^{\circ}$的角（即$120^{\circ}$）所对弧上张开的弦长的一半，即半径$3\;438$等份中的$2\;977$等份.$\dfrac{2\;977}{3\;438}$和我们今日所用的$\sin{60^{\circ}}$值两者之间的等价性是一目了然的.印度人极少使用余弦函数，他们几乎总是使用余角的正弦函数.也没有什么证据说明他们使用过正切函数.

印度人是熟悉简单三角函数的关系的，他们用这些关系计算过从$0^{\circ}$到$90^{\circ}$角的正弦函数，以$(3\dfrac{3}{4} )^{\circ}$或直角的$\dfrac{1}{24}$为间隔.他们的计算方法如下：

$$\sin{90^{\circ}} =\dfrac{1}{2} \mathrm{chord} \;180^{\circ} =3\;438$$

$$\sin{30^{\circ}} =\dfrac{1}{2} \mathrm{chord} \;60^{\circ} =\dfrac{1}{2} r=1\;719$$

参照图$10$，我们注意到：

$\lbrace \mathrm{chord} \;120^{\circ} \rbrace^2 +\lbrace \mathrm{chord} \;(180^{\circ} -120^{\circ}) \rbrace^2 =($直径$)^2$

即$\sin{}^2 60^{\circ} +\cos{}^2 60^{\circ} =r^2=(3\;438)^2$

或$\sin{}^2 60^{\circ} +\sin{}^2 30^{\circ}=(3\;438)^2$

因而$\sin{}^2 60^{\circ} =(3\;438)^2 -(1\;719)^2$

或$\sin{60^{\circ}} =2\;977$

同理$\sin{}^2 45^{\circ} +\cos{}^2 45^{\circ} =(3\;438)^2$

因此$\sin{45^{\circ}} =\dfrac{3\;438}{\sqrt{2} } =2\;430$

他们还知道如何处理半角公式

$$2\sin{}^2 \dfrac{1}{2} \theta =1-\cos{\theta } $$

他们把它写成了

$$\sin{\dfrac{1}{2} \theta } =\sqrt{1\;719\lbrace 3\;438-\sin{(90^{\circ} -\theta )} \rbrace } $$

这是他们从托勒密所发现的公式中推导出来的，推导方法如下：

$$(\mathrm{chord} \;\theta )^2 =\dfrac{1}{2} (\mathrm{chord} \;180^{\circ} )\lbrace \mathrm{chord} \;180^{\circ}-\mathrm{chord} \;(180^{\circ} -2\theta ) \rbrace $$

即$(2\sin{\dfrac{1}{2} \theta } )^2 =\dfrac{1}{2} \cdot 2r\lbrace 2r-2\sin{(90^{\circ} -\theta )} \rbrace $

或$4\sin{}^2 \dfrac{1}{2} \theta =2r\lbrace r-\sin{(90^{\circ} -\theta )} \rbrace $

或$\sin{}^2 \dfrac{1}{2} \theta =\dfrac{1}{2} \cdot 3\;438 \lbrace 3\;438-\sin{(90^{\circ} -\theta )} \rbrace (r=3\;438)$

这就导致上述结果.他们用这一公式从$\sin{60^{\circ}}$的已知值，推出了$60^{\circ}$的各倍分角的正弦函数值，直到$3.75^{\circ}$.例如，求$\sin{15^{\circ}} $时，他们就在上面的公式中令$\theta =30^{\circ} $，因此

$$\begin{align}
& \sin{15^{\circ}} \\
= & 1\;719(3\;438-\sin{60^{\circ}} ) \\
= & 1\;719(3\;438-2\;977 ) \\
= & 1\;719\times 461
\end{align}$$

所以$\sin{15^{\circ}} =890.2$.如果用半径的分数来表示，它就是$\dfrac{890.2}{3\;438} $或$0.258\;8$.从$\sin{15^{\circ}}$很容易就能算出$\sin{7.5^{\circ}}$和$\sin{3.75^{\circ}}$.

波什迦罗（$12$世纪）可能是印度数学家当中最伟大的一位.他的不朽贡献是关于不定方程的研究，我们不久将会谈到.他在三角学方面也有著作，而且好像已经有了把正弦函数看做一个比值的概念，即弧与半径之比的概念.因他曾写过$\sin{1^{\circ}} =\dfrac{10}{573} $，他可能和前人一样，把圆周分成$21\;600$等份，并接受了阿耶波多的以比值$3\;438$作为半径量度的做法，而导出$\sin{1^{\circ}}$的这个值，亦即

$$\sin{1^{\circ}} =\dfrac{弧1^{\circ}}{半径} =\dfrac{1}{360} \times \dfrac{21\;600}{3\;438} =\dfrac{10}{573} $$

同理，$3.75^{\circ}$的正弦值可作为$\dfrac{1}{24}$直角所对的弧与半径之比而得出，因此可表示为$\dfrac{100}{1\;528}$.

在印度的文献中，还没有什么证据说明印度人曾经研究过球面三角学.虽然如此，他们在天文学方面的研究，表明他们是熟悉那些球面三角解法的基础原理的.

现在我们转向阿拉伯人.在历代伊斯兰教领袖的激励下，这个民族显示他们乃是勤劳而有耐心的观察者.他们很少有什么创造性的贡献，但当他们获得《至大论》的抄本后，立即采用了托勒密计算各种角度的弦长的方法.他们与印度人也有相当的商业往来，并且从印度人那里获得了许多常用的公式以及正弦数值表.在阿拉伯人中，最著名的一位是阿尔巴塔尼（死于$929$年）.他编写过一些表，$12$世纪时蒂沃利的柏拉图曾把这些表译成拉丁文，书名《星象学》（$De\;Scientia\;Stellarum$）.他仿照印度人那样有规则地使用了正弦函数，亦即半弦数，来代替托勒密的整弦数.他还编过一种表，能给出长度为$12$单位的杆子在太阳高度为$1^{\circ}$，$2^{\circ}$，$3^{\circ} \cdots $时投影之长，因此我们从他那里可以得到余切表和正切表.他是熟悉托勒密的三角形公式的，包括球面三角形$ABC$的公式：

$$\cos{A} =\cos{B} \cos{C} +\sin{B} \sin{C} \cos{A} $$

在$10$世纪末，著名的阿布尔$\cdot $瓦法曾经提出过一种用重复相除的方法，用于计算每半度角的正弦值，达到非常高的准确度.他所算出的$\sin{30’}$的值，准确到小数点后九位数字.他是第一个把正切函数作为一个独立函数引入，而不仅是作为正弦与余弦之比值引入的人.开罗的伊本$\cdot $尤诺斯（死于$1008$年）也在三角函数的计算方面显示了相当的才能.此外，乌勒$\cdot $贝格（$1393-1449$）曾使用今天应写成$\sin{}^3 \theta =\dfrac{1}{4} (3\sin{\theta } -\sin{3\theta} )$的关系式编造过正弦表.

三角学在波伊尔巴赫（$1423-1461$）、雷格蒙塔努斯（原名约翰$\cdot $缪勒）、雷蒂库斯和皮蒂斯楚斯（$1561-1613$）等人手中获得了进一步的发展.他们的贡献将在下章叙述.