代数学引论 在线阅读 聂灵沼 丁石孙 高等教育出版社 第2版

集合与整数

集合是数学的基本概念之一.它是具有一定属性的事物形成的一个集体.根据这属性可以区别一个事物属于或不属于这个集合.例如空间的点集、实系数多项式集合、定义在区间$\left[ 0,1\right]$上的实函数集合等.本章主要讨论一个集合上的等价关系、偏序关系以及整数的算术性质.关于集合的子集、交集、并集以及一个集合到另一个集合的映射等概念，在高等代数课程中已有介绍，在这里不再重复.

集合上的等价关系

在一个集合的元素之间常常存在某种关系.例如，两个$n\times n$的复矩阵的相似或不相似；空间两直线平行或不平行；数学分析中两个哥西序列的等价或不等价，都是特殊集合上的重要关系.

设$S$为一非空集合，$a,b,c,\cdots$表示它的元素.设在$S$中任意两个元素之间存在(或不存在)某种属性$R$.只要$R$满足下面的条件，即对于$S$中任一对有次序的元素$a,b$来说，$a,b$有这种属性$R$或者$a,b$没有这种属性$R$，这两者必定有一成立而且只有一成立，那么我们说$R$是集合$S$上的一个二元关系，或简称关系.若$a,b$有关系$R$，则记作$aRb$.

上面列举的“相似”、“平行”和“等价”都是它们的相应集合上的二元关系.又如，实数集合上的大小关系“$\leq$”，整数集合上的整除关系$a\arrowvert b$都是该集合上的二元关系.再如一个非空集合$S$中元素之间的相等(或不相等)，子集之间的包含(或不包含)分别是$S$上和$S$上的幂集$P(S)$上的二元关系.所谓$S$的幂集$P(S)$就是$S$的所有子集作元素构成的集合.

非空集合$S$上一个二元关系$R$还可用笛卡尔积$S\times S$的一个子集$T$表示.$T$规定如下

$$T=\lbrace (a,b)\in S\times S\arrowvert a,b有关系R\rbrace .$$

于是可以说，元素$a,b$有关系$R$当而且仅当$(a,b)\in T$.$T$称为关系$R$在$S\times S$中的图象.反之，$S\times S$的任一个子集$T$可以给出$S$上的一个二元关系$R$，称元素$a,b$有关系$R$当有仅当$(a,b)\in T$.由此可知$R$满足二元关系的条件.

按照矩阵的相似关系可以将$n\times n$复矩阵分成若干相似类，使之每一类有一个标准形作为代表；按照哥西序列的等价关系可以将哥西序列分成一些等价类，使之每一类代表一个实数.这些都是数学中常见的基本方法.“相似”和“等价”它们有三条共性，就是反身性、对称性和传递性.

定义1如果一个非空集合$S$的一个二元关系$R$满足下列三条：

$(i)$反身性.$aRa$，对所有$a\in S$，

$(ii)$对称性.若$aRb$，则$bRa$，

$(iii)$传递性.若$aRb$且$bRc$，则$aRc$，

则称$R$是$S$的一个等价关系.等价关系$R$通常记成“$\sim$”.

显然，“相似”、“平行”、“哥西序列等价”都是等价关系.但是“$\leq$”和“$a\arrowvert b$”则不是等价关系.而”$=$”和“$a\arrowvert b$且$b\arrowvert a$”是等价关系.

如果非空集合$S$的一组子集$\lbrace S_{\lambda}\arrowvert \lambda \in I\rbrace $，$I$为指标集，满足下列条件：

$(1)S=\displaystyle \underset{\lambda \in I}{\bigcup}S_{\lambda},$

$(2)S_{\lambda}\cap S_{\mu}=\varnothing ,\lambda \neq \mu ,\lambda ,\mu \in I$,

则${S_{\lambda}}$叫做$S$的一个划分.

非空集合$S$的任一个等价关系$\sim$确定$S$的一个划分如下：对每个元素$a\in S$，规定

$$S_{a}=\lbrace x\in S\mid x\sim a\rbrace $$

这样得到$S$的一组子集$\lbrace S_{a}\mid a\in S\rbrace $.证明它是$S$的一个划分.首先，由于反身性，$a\sim a$，所以$a\in S_{a}$，于是

$$S=\underset{a\in S}{\bigcup}S_{a}.$$

其次证明，若$S_{a}\cap S_{b}\neq \varnothing$，则$a\sim b$且$S_{a}=S_{b}$.设$S_{a}\cap S_{b}\neq \varnothing$，取一个$c\in S_{a}\cap S_{b}$，于是$c\sim a$，$c\sim b$，由对称性，$a\sim c$，再由传递性，得$a\sim b$.其次对任一元素$x\in S_{a}$，有$x\sim a$，由传递性得$x\sim b$，从而$x\in S_{b}$，所以$S_{a}\subset S_{b}$.再由对称性，$b\sim a$，同理得$S_{b}\subset S_{a}$.所以$S_{a}=S_{b}$.由此可知$\lbrace S_{a} \arrowvert a\in S\rbrace$，把重复的去掉之后，就是$S$的一个划分.这个划分中的每个元素叫做由等价关系确定的等价类.

反之，$S$的任一个划分$\lbrace S_{\lambda}\mid \lambda \in I\rbrace$决定一个等价关系如下：规定

$$a\sim b\Leftrightarrow a,b 属于同一个S_{\lambda}.$$

首先，由划分的定义可知$a,b$属于同一个$S_{\lambda}$或者$a,b$分属于不同的$S_{\lambda}$，这两者有一而且只有一成立.因而”$\sim$”是一个二元关系.进一步由划分的定义，不难证明，“$\sim$”是一个等价关系，而且这个等价关系如上决定的划分就是原来的划分.

一个集合的等价关系的重要性在于由它可以产生出新的集合.设”$\sim$”是非空集合$S$的一个等价关系.如上，”$\sim$”将$S$分成一些互不相交的等价类$\lbrace S_{\lambda}\mid \lambda \in I\rbrace$的并.为表法简明起见，在每个等价类$S_{\lambda}$中取一个代表$a$，将$S_{\lambda}$写成$\overline{a}$.这种表示与代表的取法无关，就是说，$\overline{a} =\overline{b}$当且仅当$a\sim b$.用这些等价类$\overline{a} ,\overline{b} ,\cdots$作元素得到一个新的集合，记作$S/\sim $，叫做$S$关于等价关系$\sim$的商集.今后将会看到，对于各种不同的具体集合$S$和等价关系$\sim$，商集$S/\sim$将会有它崭新的意义.

例三维仿射空间的直线集合按平行关系分成一些平行直线束，设想每一平行直线束相交于同一个无穷远点.这样，以平行直线束为元素得到的商集就表示一个无穷远平面，它是一个射影平面.把这个射影平面添加到三维仿射空间就得到一个三维射影空间.这就是历史上将仿射空间扩充成射影空间的朴素的几何直观的方法.

集合$S$到商集$S/\sim$存在一个自然映射

$$\nu :x\mapsto \overline{x},x\in S.$$

它是一个满射，而且$\nu (a)=\nu (b)$当且仅当$a\sim b$.

反之，设$\varphi$是集合$S$到集合$T$的一个映射.于是在$S$上可以如下定义一个关系$\sim$:

$$a\sim b当且仅当\varphi (a)=\varphi (b),a,b\in S.$$

容易看出，这是一个等价关系.而且$\varphi$诱导出商集$S/\sim$到$T$的一个映射$\overline{\varphi}$如下：

$$\overline{\varphi}(\overline{x})=\varphi (x),x\in S.$$

显然$\overline{\varphi}$是单一的.这样，映射$\varphi$就分解成一个自然映射$\nu :S\to S/\sim$和一个单射$\overline{\varphi}$的积

$$\varphi=\overline{\varphi} \cdot \nu.$$

用图表示就是

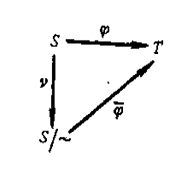
综上所述，我们得到

定理1 非空集合$S$上的一个等价关系$\sim$的一个商集$S/\sim$并诱导出一个自然映射$\nu :S\to S/\sim$使得$x\sim y$，$x$，$y\in S\Leftrightarrow \nu (x)=\nu (y)$，反之，任一个集合映射$\varphi :S\to T$决定$S$上的一个等价关系$\sim$使得$x\sim y$，$x$，$y\in S\Leftrightarrow \varphi (x)=\varphi (y)$.而且$\varphi$诱导出商集$S/\sim$到$T$的单一映射$\overline{\varphi}$：$\overline{\varphi}(\overline{x})=\varphi (x)$，$x\in S$，使得$\varphi$有分解

$$\varphi =\overline{\varphi} \cdot \nu.$$