几个典型问题

本节列出水平各异的四个问题，前三个问题互不相同，用于引起对不同类型的域，对线性空间，对群及其表示的研究，它们的代数理论将要在下面谈到.许多专门著作是为了“解答”这类问题而写的.第四个问题是为了引出线性方程组的研究，读者不看后面解线性方程组一节的内容，自己试着去解决它是有益处的.

1.方程的根式解问题

从初等代数已知求二次方程$ax^2+bx+c=0$的解$x_1 ,x_2 $的公式

$$x_{1,2} =\dfrac{-b\pm \sqrt{b^2-4ac} }{2a} \tag{1}$$

在三次方程

$$x^3+ax^2+bx+c=0$$

中，用$x-\dfrac{a}{3} $代替$x$，得到形如$x^3+px+q=0$的方程.方程的三个根$x_1 ,x_2 ,x_3 $可由它的系数表示成下述形式.若令

$$
\begin{array}{cc}
D=-4p^3-27q^3, & \varepsilon =\dfrac{-1+\sqrt{-3} }{2}, \
u=\sqrt[3]{-\dfrac{27}{2} q+\dfrac{3}{2} \sqrt{-3D} }, & v=\sqrt[3]{-\dfrac{27}{2} q-\dfrac{3}{2} \sqrt{-3D} } \
\end{array}\ \tag{2}
$$

(立方根满足$uv=-3p$)，则可证明

$$x_1 =\dfrac{1}{3}(u+v),x_2 =\dfrac{1}{3}(\varepsilon ^2u+\varepsilon v),x_3 =\dfrac{1}{3}(\varepsilon u+\varepsilon ^2v).\tag{3}$$

与公式$(1)$一样，对字母系数$a,b,c,p,q$的任意数值，例如任意有理数值，公式有效.公式$(2)$和$(3)$叫做卡尔达诺公式($1545$年)，对此作出贡献的还有其他文艺复兴时期的意大利数学家(费罗，塔尔塔利亚).对四次议程也找到了类似的公式，而寻求五次一般方程根式解的努力延续了几乎$300$年之久，但未能获得成功.直到$1813$年鲁菲尼(第一次，粗略地)和$1827$年阿贝尔(独立地，完全严格地)证明了下述定理，$n$次一般方程.

$$x^n+a_1 x^{n-1}+\cdots +a_n =0$$

当$n > 4$时没有根式解.

在这一领域中的本质发现是$1831$年由二十岁的伽罗瓦得到的(直到$1846$年才为世人所知)，他给出了对任意方程(例如有理系数方程)可根式求解的判定法则，而不仅仅局限于一般$n$次方程，对每一个$n$次多项式(方程)，伽罗瓦给出了一个分裂域和由这个域的自同构组成的有限集(基数不超过$n!$)，现在称之为域的(或原多项式的)伽罗瓦群.

我们把伽罗瓦理论放到$[BAⅢ]$中更详细地讲述.此处仅完全根据内在的性质区分出一类特殊的群，称之为可解群.其结论是，$n$次有理系数方程可用根式求解，当且仅当它对应的伽罗瓦群是可解群.例如，设给出五次方程

$$x^5-ax-1=0,$$

其中$a$是一个整数.它对应的伽罗瓦群$G_a$以某种复杂的方式依赖于$a$；当$a=0$时，$G_0$是$4$阶循环群(根据定义，所有的循环群都是可解的)，从而方程

$$x^5-1=0$$

是可以根式求解的.反之，$G_1$与$120$阶对称群$S_5$有相同的结构，而后者在$[BAⅢ]$中证明是一个不可解群.因而方程

$$x^5-x-1=0$$

是不能用根式求解的.

我们要注意，从应用的角度出发，一个代数方程的解能否用根式明显地表达出来，并没有本质上的重要意义；反而是计算根的各种近似方法更实用一些.但这丝毫无损于伽罗瓦理论的辉煌，他的成就对后来数学的发展在思想上影响深远.从那时起，伽罗瓦奠定了群论的基础.他建立的分裂域的子域与其伽罗瓦群的子群之间的一一对应到$20$世纪已用新的抽象结构加以充实，成为数学研究中不可缺少的工具.

2.多原子分子的状态问题

每一个分子都可以被看作是一个粒子系，即原子核及环绕原子核的电子.如果在初始时刻粒子系接近于平衡状态，则在一定条件下，粒子系中的粒子总是停留在平衡位置附近，不会得到较高的速度.这种类型的运动叫作相对不平衡状态的振动，并称这样的系统是稳定的.

我们知道，分子在平衡位置附近的任何小振动都是所谓正常振动的叠加.在很多情况下，注意到分子内部的对称性，可以确定分子的势能及其正常频率.分子结构的对称性用分子的点群来描述.这一有限群的不同的实现(即它的不可约表示)及其与这些实现相联系的群上的函数(表示的特征标)确定了分子振动的参数.

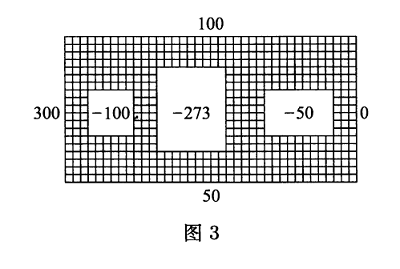
例如水分子$H_2 O$(见图$1$)对应于克莱因四元群(两个二阶循环群的直积)；而磷分子$P_4 $(见图$2$)则形如正四面体，磷原子分布在顶点上，$P_4 $对应于对称群$S_4 $，其阶为$24$.它的不可约表示在$[BAⅢ]$中给出.

今天分子结构理论的发展没有群论的帮助是难以想象的.群论在很早以前就被应用到结晶学上.早在$1891$年，伟大的俄罗斯结晶学家费得洛夫以及后来德国科学家绍恩费里斯找到了$230$种空间晶体群，描述了自然界已发现的一切晶体对称.从那时起，群论一直被用来研究对称性对晶体物理性质的影响.

通信编码问题

在地面上或太空中建立自动通信系统时，被用作基本信息单位的通常是一个有序序列，称之为行(或字)：

$$a=(a_1 ,a_2 ,\cdots ,a_n ),$$

其长度为$n$,$a_i=0$或$a_i=1$.因为模$2$的加法和乘法运算在计算机上很好实现，而信号$1,0$本身以电子信号的形式来传送又很方便($1$和$0$的区分或按照信号时间的相位，或按照信号的有无)；无怪乎$GF(2)$(见第$4$章$\S 3$)被通信专家们用来加工信息.有时将$a_i$看作其他有限域中的元素也很方便.

为了排除干扰(大气放电，宇宙噪音等)，这些干扰可能会把$0$变成$1$，把$1$变成$0$，必须使$a$足够长，并采用专门的编码系统，即从字的全部集合$S$中挑选出由传输行(字码)构成的子集$S_0$(码)，以便当发生的误差不是太大时，从所收到的变形了的字$a’$恢复到原来的$a$。这样就出现了纠错码.

编码的代数理论近年来发展迅速，给出了许多巧妙的编码方法，该理论主要涉及特殊线性编码：$S_0$的选取依赖于特殊长方矩阵的构造和线性方程组的解，它们的系数属于一个给定的有限域，在第$4$章中将给出一个简单的例子.

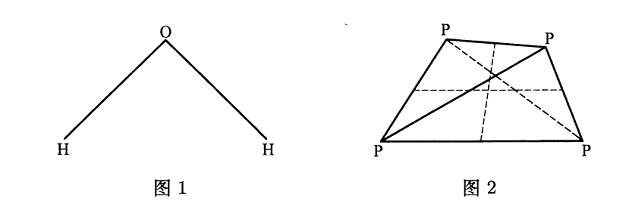
平板受热问题

带有三个孔的矩形平板(见图$3$)被被当作一种奇妙装置的阀门，以便得到低温.阀门由正方形方格构成的一个网覆盖着.位于网的四条边界上的正方形的顶点称为边界点，而其他的顶点叫作内点.测量表明，当加热或冷却时，任一内点的温度是它相邻的四个顶点(内点或边界点)温度值的算术平均.我们希望边界点的温度取图$3$所示的值.这是可能的吗？如果可能，试问内点的温度分布是不是唯一确定的？