浙江大学2010年攻读硕士学位研究生入学考试试题
科目名称:数学分析
一、计算下列极限和积分($60$分,每小题$10$分)
$(1)$ $\quad \displaystyle \lim_{n\to \infty }\sum_{k=n^2}^{(n+1)^2}\dfrac{1}{\sqrt{k}} ;$
解:由于
$$\dfrac{2n+2}{n+1} \leq \displaystyle \sum_{k=n^2}^{(n+1)^2}\dfrac{1}{\sqrt{k}} \leq \dfrac{2n+2}{n} ,$$
而
$$\displaystyle \lim_{n\to \infty } \dfrac{2n+2}{n+1}=\lim_{n\to \infty } \dfrac{2+\dfrac{2}{n} }{1+\dfrac{1}{n} } =2,\lim_{n\to \infty } \dfrac{2n+2}{n} =\lim_{n\to \infty } (2+\dfrac{2}{n})=2 $$
故
$$\displaystyle \lim_{n\to \infty }\sum_{k=n^2}^{(n+1)^2}\dfrac{1}{\sqrt{k}} =2.$$
$(2)$ $\quad \displaystyle \iint_{[0,\pi ]\times [0,1]} y\sin{(xy)}\,dx\,dy;$
解:
$$\begin{align}
& \iint_{[0,\pi ]\times [0,1]} y\sin{(xy)}\,dx\,dy \\
= & \int_0^1 \,dy\int_0^{\pi } y\sin{(xy)} \,dx \\
= & \int_0^1 -\cos{(xy)}{\Big|}_0^{\pi }\,dy \\
= & \int_0^1 [1-\cos{(\pi y)}]\,dy \\
= & (y-\dfrac{\sin{(\pi y)}}{\pi}){\Big|}_0^1 \\
= & 1-\dfrac{\sin{(\pi \cdot 1)}}{\pi }-0+\dfrac{\sin{(\pi \cdot 0)}}{\pi } \\
= & 1
\end{align}$$
$(3)$ $\quad \displaystyle \lim_{x\to 0} \dfrac{e^x \sin{x}-x(1+x)}{\sin{}^3 x} ;$
解:
$$\begin{align}
& \lim_{x\to 0} \dfrac{e^x \sin{x}-x(1+x)}{\sin{}^3 x} \\
= & \lim_{x\to 0} \dfrac{e^x \sin{x}-x(1+x)}{x^3} (\because \sin{x}\sim x ,x\to 0) \\
= & \lim_{x\to 0} \dfrac{e^x \sin{x}-x-x^2}{x^3} \\
= & \lim_{x\to 0} \dfrac{e^x \sin{x}+e^x \cos{x}-1-2x}{3x^2} (\because 洛必达法则)\\
= & \lim_{x\to 0} \dfrac{e^x \sin{x}+e^x \cos{x}+e^x \cos{x}-e^x \sin{x}-2}{6x} (\because 洛必达法则) \\
= & \lim_{x\to 0} \dfrac{2e^x \cos{x}-2}{6x} \\
= & \lim_{x\to 0} \dfrac{e^x \cos{x}-1}{3x} \\
= & \lim_{x\to 0} \dfrac{e^x \cos{x}-e^x \sin{x}}{3} (\because 洛必达法则)\\
= & \dfrac13
\end{align}$$
$(4)$ $\quad $计算$\displaystyle \iint_{\sum }z\,dx\,dy$,其中$\sum$是三角形$\lbrace (x,y,z):x,y,z\geq 0,x+y+z=1\rbrace $,其法方向与$(1,1,1)$方向相同;
解:
1 | Plot3D[1 - x - y, {x, 0, 1}, {y, 0, 1}, PlotRange -> {0, 1},AxesLabel -> Automatic] |
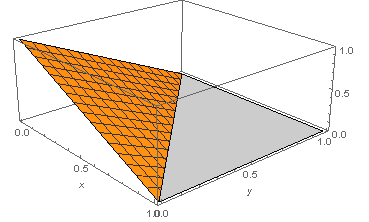
如图所示补充平面块$S_{1下} ,S_{2左} ,S_{3后}$,则$\sum +S_{1下} +S_{2左} +S_{3后}$构成封闭曲面$S$外侧,由奥高公式,所求积分
$$\begin{align}
\underset{\sum}{\iint} z\,dx\,dy & =\underset{S_{外}}{\iint} z\,dx\,dy -\underset{S_{1下}}{\iint} z\,dx\,dy -\underset{S_{2左}}{\iint} z\,dx\,dy -\underset{S_{3后}}{\iint}z\,dx\,dy \\
& =\underset{V}{\iiint} \dfrac{\partial z}{\partial z}\,dx\,dy\,dz -\underset{S_{1下}}{\iint} z\,dx\,dy -\underset{S_{2左}}{\iint} z\,dx\,dy -\underset{S_{3后}}{\iint}z\,dx\,dy \\
& =\underset{V}{\iiint}\,dx\,dy\,dz -\underset{S_{1下}}{\iint} z\,dx\,dy -\underset{S_{2左}}{\iint} z\,dx\,dy -\underset{S_{3后}}{\iint}z\,dx\,dy
\end{align}$$
对于$\displaystyle \underset{V}{\iiint}\,dx\,dy\,dz$来说,$V$在$xy$平面上的投影区域
$$D=\lbrace (x,y)\mid 0\leq y\leq 1-x,0\leq x\leq 1\rbrace $$
是$x$型区域,这里$z_1 (x,y)=0,z_2 (x,y)=1-x-y$.所以由公式
$$\displaystyle \underset{V}{\iiint}f(x,y,z)\,dx\,dy\,dz =\int_a^b \,dx \int_{y_1 (x)}^{y_2 (x)}\,dy \int_{z_1 (x,y)}^{z_2 (x,y)} f(x,y,z)\,dz$$
有
$$\begin{align}
\underset{V}{\iiint}\,dx\,dy\,dz & =\int_0^1 \,dx \int_0^{1-x}\,dy \int_0^{1-x-y}\,dz \\
& =\int_0^1 \,dx \int_0^{1-x}(1-x-y)\,dy \\
& =\int_0^1 \dfrac{1-2x+x^2}{2}\,dx \\
& =\dfrac{x-x^2+\dfrac{x^3}{3}}{2}{\Bigg|}_0^1 \\
& =\dfrac16
\end{align}$$
又因为$S_{2左} \bot xy$平面,$S_{3后} \bot xy$平面,故$\displaystyle \underset{S_{1下}}{\iint} z\,dx\,dy =\underset{S_{2左}}{\iint}z\,dx\,dy =0$.
$S_{1下}:Z=0$,故$\displaystyle \underset{S_{3后}}{\iint}z\,dx\,dy =\underset{S_{3后}}{\iint}0\,dx\,dy =0$.
所以,
$$\displaystyle \underset{\sum}{\iint} z\,dx\,dy=\dfrac16 -0-0-0=\dfrac16.$$
$(5)$ $\quad \displaystyle \int_0^{2\pi }\sqrt{1+\sin{x}}\,dx ;$
解:
$$\begin{align}
& \int_0^{2\pi }\sqrt{1+\sin{x}}\,dx \\
= & \int_0^{2\pi }\sqrt{1+2\sin{\dfrac{x}{2}}\cos{\dfrac{x}{2}}}\,dx \\
= & \int_0^{2\pi }\sqrt{\sin{}^2\dfrac{x}{2}+\cos{}^2\dfrac{x}{2}+2\sin{\dfrac{x}{2}}\cos{\dfrac{x}{2}}}\,dx \\
= & \int_0^{2\pi }\sqrt{\left( \sin{\dfrac{x}{2}}+\cos{\dfrac{x}{2}}\right)^2}\,dx \\
= & \int_0^{2\pi }{\Bigg|} \sin{\dfrac{x}{2}}+\cos{\dfrac{x}{2}}{\Bigg|} \,dx \\
= & \int_0^{2\pi }{\Bigg|} \sqrt{2} \sin{\left( \dfrac{x}{2}+\dfrac{\pi }{4}\right) }{\Bigg|} \,dx
\end{align}$$
1 | Plot[{Sqrt[2]*Sin[x/2 + Pi/4], Sin[x]}, {x, 0, 2 Pi},PlotStyle -> {Thick, Automatic},Epilog -> {PointSize[0.02], Point[{1.5 Pi, 0}]},AspectRatio -> Automatic,AxesLabel -> {"x", "Sqrt{2}*Sin[x/2+Pi/4]"},PlotRange -> {-Sqrt[2], Sqrt[2]}] |
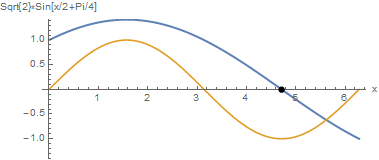
根据函数图象知,当$0\leq x\leq \dfrac32 \pi $时,$\sqrt{2} \sin{\left( \dfrac{x}{2}+\dfrac{\pi }{4}\right) } \geq 0$;当$\dfrac32 \pi \leq x\leq 2\pi $时,$\sqrt{2} \sin{\left( \dfrac{x}{2}+\dfrac{\pi }{4}\right) } \leq 0$.
故
$$\begin{align}
& \int_0^{2\pi }\sqrt{1+\sin{x}}\,dx \\
= & \int_0^{2\pi }{\Bigg|} \sqrt{2} \sin{\left( \dfrac{x}{2}+\dfrac{\pi }{4}\right) }{\Bigg|} \,dx \\
= & \int_0^{\frac32 \pi } \sqrt{2} \sin{\left( \dfrac{x}{2}+\dfrac{\pi }{4}\right) } \,dx -\int_{\frac32 \pi }^{2\pi } \sqrt{2} \sin{\left( \dfrac{x}{2}+\dfrac{\pi }{4}\right) } \,dx \\
= & 2\sqrt{2}\left[ \int_0^{\frac32 \pi } \sin{\left( \dfrac{x}{2}+\dfrac{\pi }{4}\right) } \,d\left( \dfrac{x}{2}+\dfrac{\pi }{4}\right) -\int_{\frac32 \pi }^{2\pi } \sin{\left( \dfrac{x}{2}+\dfrac{\pi }{4}\right) } \,d\left( \dfrac{x}{2}+\dfrac{\pi }{4}\right) \right] \\
= & 2\sqrt{2}\left[ \left(-\cos{\left( \dfrac{x}{2}+\dfrac{\pi }{4}\right) } \right) {\Bigg|}_0^{\frac32 \pi}-\left( -\cos{\left( \dfrac{x}{2}+\dfrac{\pi }{4}\right) } \right) {\Bigg|}_{\frac32 \pi}^{2\pi} \right] \\
= & 2\sqrt{2}\left[ \left(-\cos{\left( \dfrac{x}{2}+\dfrac{\pi }{4}\right) } \right) {\Bigg|}_0^{\frac32 \pi}+\cos{\left( \dfrac{x}{2}+\dfrac{\pi }{4}\right) } {\Bigg|}_{\frac32 \pi}^{2\pi} \right] \\
= & 2\sqrt{2}\left[ \left( -\cos{\left( \dfrac{\dfrac{3}{2}\pi }{2}+\dfrac{\pi }{4}\right) } -\left( -\cos{\left( \dfrac{0}{2} +\dfrac{\pi }{4} \right) } \right)\right) +\left( \cos{\left( \dfrac{2\pi }{2} +\dfrac{\pi }{4} \right) }-\cos{\left( \dfrac{\dfrac{3}{2}\pi }{2} +\dfrac{\pi }{4} \right) } \right) \right] \\
= & 2\sqrt{2} \left[ -\left( 1+\dfrac{\sqrt{2}}{2} \right) +\left( -\dfrac{\sqrt{2}}{2} +1\right) \right] \\
= & 4\sqrt{2}.
\end{align}$$
$(6)$ $\quad \displaystyle \int_0^1 \dfrac{\ln{(1+x)}}{1+x^2} \,dx$.
解:令$x=\tan{\theta }$,则$\theta =\arctan{x}$,$d\theta =\dfrac{1}{1+x^2}\,dx$,又因为$x\in [0,1]$,故$\theta \in [0,\dfrac{\pi }{4}]$.
$$\begin{align}
& \int_0^1 \dfrac{\ln{(1+x)}}{1+x^2} \,dx \\
= & \int_0^1 \ln{(1+x)}\cdot \dfrac{1}{1+x^2} \,dx \\
= & \int_0^{\frac{\pi }{4}} \ln{(1+\tan{\theta })}\,d\theta \\
= & \int_0^{\frac{\pi }{4}} \ln{(1+\dfrac{\sin{\theta }}{\cos{\theta }})}\,d\theta \\
= & \int_0^{\frac{\pi }{4}} \ln{\dfrac{\cos{\theta } +\sin{\theta}}{\cos{\theta}}}\,d\theta \\
= & \int_0^{\frac{\pi }{4}} \ln{\left( \cos{\theta } +\sin{\theta}\right) }\,d\theta -\int_0^{\frac{\pi }{4}} \ln{\cos{\theta } }\,d\theta \\
= & \int_0^{\frac{\pi }{4}} \ln{\left[ \sqrt{2} \left( \cos{\theta } \cdot \cos{\dfrac{\pi }{4}}+\sin{\theta} \cdot \sin{\dfrac{\pi }{4} }\right) \right] }\,d\theta -\int_0^{\frac{\pi }{4}} \ln{\cos{\theta } }\,d\theta \\
= & \int_0^{\frac{\pi }{4}} \ln{\left( \sqrt{2} \cdot \cos{\left( \theta -\dfrac{\pi }{4} \right) }\right) }\,d\theta -\int_0^{\frac{\pi }{4}} \ln{\cos{\theta } }\,d\theta \\
= & \int_0^{\frac{\pi }{4}} \ln{\left( \sqrt{2} \right) }\,d\theta +\int_0^{\frac{\pi }{4}} \ln{\left( \cos{\left( \theta -\dfrac{\pi }{4} \right) } \right) }\,d\theta-\int_0^{\frac{\pi }{4}} \ln{\cos{\theta } }\,d\theta \\
= & \ln{2^{\frac12 }} \int_0^{\frac{\pi }{4}} \,d\theta +\int_0^{\frac{\pi }{4}} \ln{\left( \cos{\left( \theta -\dfrac{\pi }{4} \right) } \right) }\,d\left( \theta -\dfrac{\pi }{4} \right) -\int_0^{\frac{\pi }{4}} \ln{\cos{\theta } }\,d\theta
\end{align}$$
对于积分$\displaystyle \int_0^{\frac{\pi }{4}} \ln{\left( \cos{\left( \theta -\dfrac{\pi }{4} \right) } \right) }\,d\left( \theta -\dfrac{\pi }{4} \right) $,令$t=\theta -\dfrac{\pi }{4} $,则因为$\theta \in [0,\dfrac{\pi }{4}]$,故$t \in [-\dfrac{\pi }{4},0]$,于是
$$\begin{align}
& \int_0^1 \dfrac{\ln{(1+x)}}{1+x^2} \,dx \\
= & \ln{2^{\frac12 }} \int_0^{\frac{\pi }{4} } \,d\theta +\int_0^{\frac{\pi }{4} } \ln{\left( \cos{\left( \theta -\dfrac{\pi }{4} \right) } \right) }\,d\left( \theta -\dfrac{\pi }{4} \right) -\int_0^{\frac{\pi }{4}} \ln{\cos{\theta } }\,d\theta \\
= & \dfrac{1}{2} \ln{2} \left( \dfrac{\pi }{4} -0\right) +\int_{-\frac{\pi }{4} }^0 \ln{\cos{t} }\,dt-\int_0^{\frac{\pi }{4} } \ln{\cos{\theta } } \,d\theta \\
= & \dfrac{\pi }{8} \ln{2} (\because \int_{-\frac{\pi }{4} }^0 \ln{\cos{t} }\,dt =\int_0^{\frac{\pi }{4} } \ln{\cos{\theta } } \,d\theta )\\
\end{align}$$
二、($15$分)设$a_n =\sin{a_{n-1} }$,$n\geq 2$,且$a_1 > 0$,计算$\displaystyle \lim_{n\to \infty }\sqrt{\dfrac{n}{3}} a_n$.
解:$(1)$ 先证明$\displaystyle \lim_{n\to \infty } a_n =\lim_{n\to \infty } \mid a_n \mid =0$.
因为$a_1 > 0,\mid a_n \mid =\mid \sin{\mid a_{n-1} \mid } \mid$,递推可知
$$0 < \mid a_n \mid =\mid \sin{\mid a_{n-1} \mid } \mid < \mid \mid a_{n-1} \mid \mid =\mid a_{n-1} \mid \quad (n=2,3,\cdots ),$$
表明$\mid a_n \mid$单调递减且有下界$0$,$\displaystyle \lim_{n\to \infty } \mid a_n \mid$存在.记$\displaystyle \lim_{n\to \infty } \mid a_n \mid =A$,对$\mid a_n \mid =\mid \sin{\mid a_{n-1} \mid } \mid$两边取极限,得$A=\mid \sin{A} \mid $,即$A=\pm \sin{A} $,可解出$A=0$,故$\displaystyle \lim_{n\to \infty } \mid a_n \mid =0$.
因此,对任给的$\varepsilon > 0$,由$\displaystyle \lim_{n\to \infty } \mid a_n \mid =0$知:存在$N$,当$n > N$时,$\mid \mid a_n \mid -0 \mid < \varepsilon $,故当$n > N$时,有
$$\mid a_n -0\mid =\mid a_n \mid =\mid \mid a_n \mid \mid =\mid \mid a_n \mid -0\mid < \varepsilon ,$$
即有:
$$\mid a_n -0\mid < \varepsilon ,$$
所以$\displaystyle \lim_{n\to \infty } a_n =0$.
$(2)$ 分类讨论.
当$a_1 =k\pi ,k=1,2,\cdots $时,则
$$a_n =\sin{a_{n-1} } =\cdots =\sin{(\cdots (\sin{a_1 }))} =\sin{(\cdots (\sin{k\pi }))} =0 ,$$
所以,
$$\displaystyle \lim_{n\to \infty }\sqrt{\dfrac{n}{3}} a_n = \lim_{n\to \infty }\sqrt{\dfrac{n}{3}} \cdot 0 =0.$$
当$a_1 \neq k\pi ,k=1,2,\cdots $时,由函数$\sin{x}$的周期性,可以知当$2k\pi < a_1 < 2k\pi +\pi $,$k=1,2,\cdots $时,$a_n > 0$;当$2k\pi +\pi < a_1 < 2k\pi +2\pi $,$k=1,2,\cdots $时,$a_n < 0$.
因此,要计算出$\displaystyle \lim_{n\to \infty }\sqrt{\dfrac{n}{3}} a_n =\pm 1$.即要计算
$$\displaystyle \lim_{n\to \infty }na_n^2 =3\quad 或\quad \lim_{n\to \infty } \dfrac{n}{\dfrac{1}{a_n^2 }}=3.$$
用$\dfrac{\infty }{\infty }$型的$\text{Stolz}$公式
$$\begin{align}
& \lim_{n\to \infty } \dfrac{n}{\dfrac{1}{a_n^2 }} \\
= & \lim_{n\to \infty } \dfrac{n-(n-1)}{\dfrac{1}{a_n^2 } -\dfrac{1}{a_{n-1}^2 }} \\
= & \lim_{n\to \infty } \dfrac{1}{\dfrac{1}{\sin{}^2 a_{n-1} } -\dfrac{1}{a_{n-1}^2 }} \\
= & \lim_{n\to \infty } \dfrac{a_{n-1}^2 \sin{}^2 a_{n-1} }{a_{n-1}^2 -\sin{}^2 a_{n-1} } \\
= & \lim_{a\to 0 } \dfrac{a^2 \sin{}^2 a }{a^2 -\sin{}^2 a } \\
= & \lim_{a\to 0 } \dfrac{a^4}{a^2 -\sin{}^2 a} \\
= & \lim_{a\to 0 } \dfrac{4a^3}{2a-\sin{2a}} \\
= & \lim_{a\to 0 } \dfrac{12a^2}{2-2\cos{2a}} \\
= & \lim_{a\to 0 } \dfrac{6a^2}{1-\cos{2a}} \\
= & \lim_{a\to 0 } \dfrac{12a}{2\sin{2a}} \\
= & 3.
\end{align}$$
由上式,知
$$\displaystyle \lim_{n\to \infty } \dfrac{n}{\dfrac{1}{a_n^2 }} =3$$
所以
$$\displaystyle \lim_{n\to \infty } \sqrt{\dfrac{n}{3} }a_n=\pm 1.$$
综上所述,
$$\displaystyle \lim_{n\to \infty } \sqrt{\dfrac{n}{3} }a_n =\begin{cases} 1, & 若 & 2k\pi < a_1 < 2k\pi +\pi ,\\ 0, & 若 & a_1 =2k\pi ,\\ -1, & 若 & 2k\pi +\pi < a_1 < 2k\pi +2\pi ,\end{cases} k=1,2,\cdots $$
三、($15$分)设函数$f(x)$在$(-\infty ,+\infty )$上连续,$n$为奇数.证明:若$\displaystyle \lim_{x\to +\infty } \dfrac{f(x)}{x^n} =\lim_{x\to -\infty } \dfrac{f(x)}{x^n}=1$,则方程$f(x)+x^n =0$有实根.
证明:因为函数$f(x)$在$(-\infty ,+\infty )$上连续,$n$为奇数,且$\displaystyle \lim_{x\to +\infty } \dfrac{f(x)}{x^n} =\lim_{x\to -\infty } \dfrac{f(x)}{x^n}=1$,故根据连续函数的局部保号性性质,存在正数$M > 0$,使得
当$x > M$时,有$\displaystyle \lim_{x\to +\infty } \dfrac{f(x)}{x^n} \geq \dfrac{1}{2}$成立,则$f(x)\geq \dfrac{1}{2} x^n$.
当$x < -M$时,有$\displaystyle \lim_{x\to +\infty } \dfrac{f(x)}{x^n} \geq \dfrac{1}{2}$成立,则$f(x)\leq \dfrac{1}{2} x^n$.
因此,对于区间$[-M,M]$来说,有
$$f(-A)+(-A)^n \leq \dfrac{1}{2} (-A)^n +(-A)^n=-\dfrac{3}{2} A^n < 0,$$
$$f(A)+A^n \geq \dfrac{1}{2} A^n +A^n=\dfrac{3}{2} A^n > 0.$$
这时有
$$\left( f(-A)+(-A)^n \right) \left( f(A)+A^n \right) < 0$$
成立.
因此,由根的存在定理,至少存在一点$x_0 \in (-A,A)$,使得
$$f(x_0 )+x_0^n =0,$$
即方程$f(x)+x^n=0$在区间$(-A,A)$内至少有一个根.
四、($20$分)证明:$\displaystyle \int_0^{+\infty } \dfrac{\sin{xy}}{y}\,dy$在$[\delta ,+\infty )$上一致收敛(其中$\delta > 0$).
证明:作变量代换$u=xy$,得
$$\displaystyle \int_A^{+\infty } \dfrac{\sin{xy}}{y}\,dy=\int_{Ax}^{+\infty } \dfrac{\sin{u}}{u}\,du $$
其中$A > 0$.由于$\displaystyle \int_{0}^{+\infty } \dfrac{\sin{u}}{u}\,du = \int_0^1 \dfrac{\sin{u}}{u}\,du +\int_1^{+\infty } \dfrac{\sin{u}}{u}\,du$条件收敛.只需考虑$\displaystyle \int_1^{+\infty } \dfrac{\sin{u}}{u}\,du$的敛散性.因为对任意$a\geq 1$,有$\displaystyle {\Bigg|} \int_1^a \sin{u} \,du {\Bigg|} =\mid \cos{1} -\cos{a} \mid \leq 2$,而$\dfrac{1}{u}$单调趋于$0(u\to +\infty )$,故由狄利克雷判别法推知$\displaystyle \int_1^{+\infty } \dfrac{\sin{u}}{u}\,du$总是收敛的.另一方面,由于
$${\Bigg| } \dfrac{\sin{u}}{u} {\Bigg| }\geq \dfrac{\sin{}^2 u}{u} =\dfrac{1}{2u}-\dfrac{\cos{2u} }{2u} ,u\in [1,+\infty ),$$
其中$\displaystyle \int_1^{+\infty } \dfrac{\cos{2u} }{2u} \,du =\dfrac{1}{2} \int_1^{+\infty } \dfrac{\cos{t} }{t} \,dt$满足狄利克雷判别条件,是收敛的,而$\displaystyle \int_1^{+\infty } \dfrac{du}{2u}$是发散的,因此该无穷积分不是绝对收敛的.所以$\displaystyle \int_1^{+\infty } \dfrac{\sin{u}}{u}\,du$是条件收敛的.于是$\displaystyle \int_{0}^{+\infty } \dfrac{\sin{u}}{u}\,du = \int_0^1 \dfrac{\sin{u}}{u}\,du +\int_1^{+\infty } \dfrac{\sin{u}}{u}\,du$条件收敛.
根据$\displaystyle \int_{0}^{+\infty } \dfrac{\sin{u}}{u}\,du$是条件收敛,故对任给正数$\varepsilon $,总存在正数$M$,使当$A’ > M$时,就有
$$\displaystyle {\Bigg|} \int_{A’}^{+\infty } \dfrac{\sin{u}}{u}\,du {\Bigg|} < \varepsilon .$$
取$A\delta > M$,则当$A > \dfrac{M}{\delta } $时,对一切$x\geq \delta > 0$,由$\displaystyle \int_A^{+\infty } \dfrac{\sin{xy}}{y}\,dy=\int_{Ax}^{+\infty } \dfrac{\sin{u}}{u}\,du$有
$$\displaystyle {\Bigg|} \int_A^{+\infty } \dfrac{\sin{xy}}{y}\,dy {\Bigg|} < \varepsilon ,$$
所以$\displaystyle \int_0^{+\infty } \dfrac{\sin{xy}}{y}\,dy$在$x\geq \delta > 0$上一致收敛.
五、($20$分)设$f(x)$连续,证明$\text{Poisson}$公式:
$$\displaystyle \underset{x^2+y^2+z^2=1}{\int }f(ax+by+cz)\,dS =2\pi \int_{-1}^1 f(\sqrt{a^2+b^2+c^2}t)\,dt .$$
证明:要证明$\displaystyle \underset{x^2+y^2+z^2=1}{\int }f(ax+by+cz)\,dS =2\pi \int_{-1}^1 f(\sqrt{a^2+b^2+c^2}t)\,dt$,可将
$$S:x^2+y^2=1-z^2 $$
写为柱面坐标,即:
$$x=\sqrt{1-z^2}\cos{\alpha } ,y=\sqrt{1-z^2}\sin{\alpha } ,z=z,(\alpha ,z)\in \Delta =\lbrace (\alpha ,z):0\leq \alpha \leq 2\pi ,-1\leq z\leq 1\rbrace .$$
所以
$$x’_{\alpha} =-\sqrt{1-z^2}\sin{\alpha } ,y’_{\alpha}=\sqrt{1-z^2}\cos{\alpha } ,z’_{\alpha} =0,$$
$$x’_z =-\dfrac{z\cos{\alpha } }{\sqrt{1-z^2}} ,y’_z = -\dfrac{z\sin{\alpha } }{\sqrt{1-z^2}} ,z’_z =1 .$$
这时
$$\begin{align}
E & ={x’_{\alpha}}^2 +{y’_{\alpha}}^2 +{z’_{\alpha}}^2 \\
& =\left( -\sqrt{1-z^2}\sin{\alpha } \right) \left( -\sqrt{1-z^2}\sin{\alpha } \right) +\left( \sqrt{1-z^2}\cos{\alpha } \right) \left( \sqrt{1-z^2}\cos{\alpha } \right) +0\cdot 0 \\
& =1-z^2,\\
G & ={x’_z}^2 +{y’_z}^2 +{z’_z}^2 \\
& =\left( -\dfrac{z\cos{\alpha } }{\sqrt{1-z^2}} \right) \left( -\dfrac{z\cos{\alpha } }{\sqrt{1-z^2}} \right) +\left( -\dfrac{z\sin{\alpha } }{\sqrt{1-z^2}} \right) \left( -\dfrac{z\sin{\alpha } }{\sqrt{1-z^2}} \right) +1\cdot 1 \\
& =\dfrac{1}{1-z^2},\\
F & =x’_{\alpha} x’_z +y’_{\alpha} y’_z +z’_{\alpha} z’_z \\
& =\left( -\sqrt{1-z^2}\sin{\alpha } \right) \left( -\dfrac{z\cos{\alpha } }{\sqrt{1-z^2}} \right) +\left( \sqrt{1-z^2}\cos{\alpha } \right) \left( -\dfrac{z\sin{\alpha } }{\sqrt{1-z^2}} \right) +0\cdot 1 \\
& =0,\\
dS & =\sqrt{EG-F^2}\,d\alpha \,dz \\
& = \sqrt{(1-z^2)\dfrac{1}{1-z^2}-0}\,d\alpha \,dz \\
& =\,d\alpha \,dz .
\end{align}$$
故
$$\begin{align}
& \underset{x^2+y^2+z^2=1}{\int }f(ax+by+cz)\,dS \\
= & \underset{\Delta }{\iint }f(z\sqrt{a^2+b^2+c^2})\sqrt{EG-F^2}\,d\alpha \,dz \\
= & \int_0^{2\pi }\,d\alpha \int_{-1}^1 f(z\sqrt{a^2+b^2+c^2} )\,dz \\
= & 2\pi \int_{-1}^1 f(z\sqrt{a^2+b^2+c^2} )\,dz \\
= & 2\pi \int_{-1}^1 f(\sqrt{a^2+b^2+c^2} t)\,dt
\end{align}$$
六、($20$分)设$\lbrace a_n \rbrace _{n\geq 1} ,\lbrace b_n \rbrace _{n\geq 1}$为实数列,满足$(1)$.$\displaystyle \lim_{n\to \infty } \mid b_n \mid =\infty$;$(2)$.$\displaystyle \begin{Bmatrix} \dfrac{1}{\mid b_n \mid } \sum_{j=1}^{n-1} \mid b_{i+1} -b_i \mid \\ \end{Bmatrix} _{n\geq 1}$有界.证明:若$\displaystyle \lim_{n\to \infty }\dfrac{a_{n+1} -a_n }{b_{n+1} -b_n }$存在,则$\displaystyle \lim_{n\to \infty }\dfrac{a_n }{b_n }$也存在.
证明:若$\displaystyle \lim_{n\to \infty }\dfrac{a_{n+1} -a_n }{b_{n+1} -b_n }$存在,可记$c_n =\dfrac{a_{n+1} -a_n }{b_{n+1} -b_n }$,假设$\displaystyle \lim_{n\to \infty } c_n =c=0$.否则,可以用$a_n -cb_n $代替式子$c_n$里面的$a_n$,其中
$$\displaystyle \lim_{n\to \infty }\dfrac{(a_{n+1} -cb_{n+1} )-(a_n -cb_n )}{b_{n+1} -b_n } =c,$$
$$\displaystyle \lim_{n\to \infty }\dfrac{a_n }{b_n } =\lim_{n\to \infty }\dfrac{a_n -cb_n }{b_n } +c.$$
下面证明$\displaystyle \lim_{n\to \infty }\dfrac{a_n }{b_n } =0.$
因为$\displaystyle \begin{Bmatrix} \dfrac{1}{\mid b_n \mid } \sum_{j=1}^{n-1} \mid b_{i+1} -b_i \mid \\ \end{Bmatrix} _{n\geq 1}$有界,故可设其界为$M > 0$.
因为$\displaystyle \lim_{n\to \infty } c_n =c=0$,故对于任意的$\varepsilon > 0$,存在$N_1 > 0$,使得对于任意的$n > N_1 $来说,有
$$\mid c_n -0 \mid =\mid c_n \mid < \dfrac{\varepsilon }{2M} $$
成立.
对于$\displaystyle \lim_{n\to \infty } \mid b_n \mid =\infty$来说,取定上述的$N_1 $后,存在正数$N > 0$,使得当$n > N$时,有
$$\dfrac{\mid a_{N_1} \mid }{\mid b_n \mid } < \dfrac{\varepsilon }{2} $$
成立.
因为$c_n =\dfrac{a_{n+1} -a_n }{b_{n+1} -b_n }$,故有
$$\begin{align}
a_n & =a_{n-1} +c_{n-1} (b_n -b_{n-1} )\\
& =a_{n-2} +c_{n-2} (b_{n-1} -b_{n-2} )+ c_{n-1} (b_n -b_{n-1} ) \\
& \cdots \\
& =a_{N_1} +\displaystyle \sum_{i=N_1 }^{n-1} c_i (b_{i+1} -b_i ),
\end{align}$$
因此,对于任意的$\varepsilon > 0$,存在$N_1 ,N > 0$,当$n > N_1 $,且$n > N$时,有
$$\begin{align}
{\Bigg|} \dfrac{a_n }{b_n } {\Bigg|} & ={\Bigg|} \dfrac{a_{N_1} +\displaystyle \sum_{i=N_1 }^{n-1} c_i (b_{i+1} -b_i ) }{b_n } {\Bigg|}\\
& \leq {\Bigg|} \dfrac{a_{N_1} }{b_n } {\Bigg|} +\underset{N_i \leq i\leq n-1}{\max} \mid c_i \mid \cdot \underset{N_i \leq i\leq n-1}{\max} \dfrac{\displaystyle \sum_{i=N_1 }^{n-1} \mid b_{i+1} -b_i \mid }{\mid b_n \mid } \\
& \leq \dfrac{\varepsilon }{2} +\dfrac{\varepsilon }{2M} \cdot M \\
& =\varepsilon ,
\end{align}$$
由极限定义知,
$$\displaystyle \lim_{n\to \infty }\dfrac{a_n }{b_n } =0.$$
因此,若$\displaystyle \lim_{n\to \infty }\dfrac{a_{n+1} -a_n }{b_{n+1} -b_n }$存在,则$\displaystyle \lim_{n\to \infty }\dfrac{a_n }{b_n }$也存在.

