第$1$章$\S 4$的公式$(3)$和$(9)$给出了当$n=2,3$时未知数与方程个数均为$n$的线性方程组的解，这使人想到对于任意自然数$n$，类似的求解公式是否存在的问题.

归根到底，我们需要的是对所论公式中分子和分母的正确解释.我们将说明怎样将它们看作从$n$阶方阵的集合到实数集$\mathbb{R} $的一个“通用”函数$\det \colon M_n (\mathbb{R} )\to \mathbb{R}$的值.函数$\det$（行列式）的有效构造也将给出对第$2$章提出的其他许多有关矩阵问题的回答.事实上，行列式理论在数学中的作用远比我们涉及的问题广泛，并且这一理论的每一种应用都引出了行列式自身的构造方法.其中最自然的方法之一是几何方法，它基于“矩阵行列式与多维图形体积”以及外$n$形式的类比.因为需要更多的技巧，故而我们将采用“分析”方法，仅在开始时借助于几何直观.

几何背景

在引入行列式的一般概念之前，暂时忘记我们的任务，先来计算最简单的几何图形——平行六面体的体积.$n$阶方阵$A=(a_{ij} )$对应于一个平行六面体

$$\prod (A) =\prod (A^{(1)} ,A^{(2)} ,\cdots ,A^{(n)}),$$

它的边由矩阵的列$A^{(1)} ,A^{(2)} ,\cdots ,A^{(n)}$，即向量（或点）$A^{(j)} =[a_{1j} ,a_{2j} ,\cdots ,a_{nj} ]\in \mathbb{R} ^n$给出.$\prod (A)$可以看作是$\mathbb{R}^n $中的一个子集，由形如

$$x_1 A^{(1)} +\cdots +x_n A^{(n)} ,0\leq x_i \leq 1$$

的点组成（在具有直角坐标系的空间中，我们将列向量及其端点视为同一）.当$n=1$时，平行六面体叫作线段，而$n=2$时叫作平行四边形.

$n$维平行六面体的体积$\upsilon \left( \prod (A)\right)$由归纳法定义为它在$\mathbb{R}^{n-1}$中的$(n-1)$维底边的体积$\upsilon \left( \prod (A^{(1)} ,\cdots ,A^{(n-1)} )\right)$与点$A^{(n)}$到底边所在超平面的垂线段的长度$h$的乘积.例如线段$(n=1)$的体积是它的长度，平行四边形$(n=2)$的体积是它的面积.我们现在不讨论度量体积的一般理论.

直接计算表明，不计符号

$$\begin{array}{ll} n=2: & \upsilon \left(\displaystyle \prod (A^{(1)} ,A^{(2)})\right) =\begin{vmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{vmatrix} ;\\n=3: & \upsilon \left(\displaystyle \prod (A^{(1)} ,A^{(2)} ,A^{(3)} )\right) =\begin{vmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{vmatrix} \end{array} \label{1} \tag{1} $$

（$2$阶和$3$阶矩阵的行列式由第$1$章$\S 4$公式$(2)$和$(8)$给出）.

对于任意排列的多个点$A^{(1)} ,A^{(2)} ,\cdots $，无条件地保留形如$\eqref{1}$的公式是一件诱人的事情，如果运用有向体积的概念，允许平行六面体的体积取负值，这件事就有可能实现.

例如当$n=1$时，线段

的有向长度取$a < 0$.当$n=2$时若有序向量$(A^{(1)} ,A^{(2)})$与基向量$(e_1 ,e_2 )$在平面$\mathbb{R}^2$上的定向一致，平行六面体$\prod (A^{(1)} ,A^{(2)})$的面积取正号，否则取负号.在这样的意义之下，自然导出了公式$\eqref{1}$，且任意$n$阶矩阵$A$的行列式$\vert A\vert $可看作平行六面体的有向体积，记作：

$$\det A =\upsilon \left( \prod (A)\right) .$$

与标准列$E^{(j)} =[0,\cdots ,1,\cdots ,0]$相应的基向量$e_j $使得

$$A^{(j)} =\varphi _A (E^{(j)}) ,$$

它是基向量$e_j $在线性变换$\varphi _A \colon X\to AX$之下的像（见第$2$章$\S 3$）.故平行六面体$\prod (A)$是单位立方体$\prod (E)$在线性映射$\varphi _A$之下的像，而因为$\upsilon \left( \prod (E)\right) =1$，行列式$\det \varphi _A =\det A$等于有向体积的变换系数.事实上，应用$\varphi _A$，可以将任意图形的有向体积，不仅是单位立方体，转化为$\det A$（见[$BAⅡ$]）.

现在我们易于列出检验的平行四边形有向面积的一些性质：

$1)\;\upsilon \left( \prod (A^{(1)} ,A^{(2)})\right) =-\upsilon \left( \prod (A^{(2)} ,A^{(1)}) \right)$；

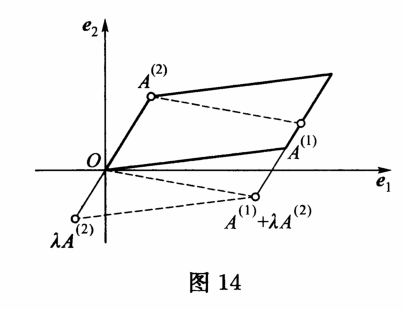
$2)\; \upsilon \left( \prod (A^{(1)} +\lambda A^{(2)} ,A^{(2)}) \right) =\upsilon \left( \prod (A^{(1)} ,A^{(2)})\right)$；

$3)\; \upsilon \left( \prod (E)\right) =1$.

性质$1)$和$3)$前面已谈到过，性质$(2)$（当$n=2$时）的图解见图$14$，它基于三角形的全等.当$n > 3$时，平行六面体体积的性质$1)-3)$不是非常直观，然而无论从任何途径引入行列式理论，都应当满足上述三条性质，这一事实是完全清楚的.此外，我们还需要得到行列式的其他一些性质，比如用于对任意给定的方阵$A$计算$\det A$，从而计算$\upsilon \left( \prod (A)\right) $，它们在算法上是可行的且易于实现的.

组合-解析方法

两个外观相近的符号

$$A=\begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \cdots & \cdots & \cdots & \cdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{pmatrix} ,\quad \det A =\begin{vmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \cdots & \cdots & \cdots & \cdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{vmatrix} .\label{2} \tag{2}$$

对于我们并不陌生，我们以后将经常地使用这两个有本质区别的符号.其中若$A$是一个填写了系数（通常为数）的正方形表格，那么这个表格的$n$阶行列式以两条垂直线为界，它是一个属于矩阵$A$的数（或表达式），由下述的完全展开式定义：

$$\det A =\sum_{\sigma \in S_n } \varepsilon _{\sigma } a_{1\sigma (1)} a_{2\sigma (2)} \cdots a_{n\sigma (n)} .\label{3} \tag{3}$$

换言之，矩阵$A=(a_{ij} )$的行列式$\det A$是取自不同行，不同列的系数$a_{ij}$的所有可能乘积的代数和.在每一个乘积中，因子按照行脚标的顺序书写，而列脚标由行脚标在置换$\sigma \in S_n $中的像$\sigma (1) ,\sigma (2) ,\cdots ,\sigma (n)$确定.在这种记法下，和式$\eqref{3}$中共有$n!$项；对应偶置换的各项取正号，而对应奇置换的各项取负号.两种加项的个数相等，均为$\dfrac{n!}{2}$，与第$1$章$\S 8$的关系式$(11)$一致.

简单的验算表明，当$n=2$和$n=3$时，公式$\eqref{3}$与我们已知的表达式相同.设$n=4$且$\sigma =(1\;2)(3\;4)$.则$\varepsilon _{\sigma } =1$，而$a_{1,\sigma (1)} a_{2,\sigma (2)} a_{3,\sigma (3)} a_{4,\sigma (4)} =a_{12} a_{21} a_{34} a_{43}$.这就表明，在四阶行列式中，加项$a_{12} a_{21} a_{34} a_{43}$取正号.仔细地写出$4$阶行列式的全部$24$项，并注意观察符号的分布是一个有益的练习，可以导致对第$1$章$\S 8$的内容的切实掌握.当$n=5$时写出$5$阶行列式$120$项的练习看来不是十分必要.根据第$1$段的看法，我们希望作为出发点的公式$\eqref{3}$可以对任意阶行列式提炼出我们需要的所有的性质.

行列式的基本性质

行列式的性质不多，但是为了表述，主要是为了理解它们，需要约定一些术语和符号.

以后我们沿用第$2$章的符号体系，用

$$A_{(i)} =(a_{i1} ,a_{i2} ,\cdots ,a_{in} ),\quad i=1,2,\cdots ,n,$$

$$A^{(j)} =[a_{1j} ,a_{2j} ,\cdots ,a_{nj} ],\quad j=1,2,\cdots ,n,$$

分别表示矩阵$A=(a_{ij} )$的第$i$行和第$j$列.矩阵$A$本身既可以写成以行为元素的矩阵

$$A=[A_{(1)} ,A_{(2)} ,\cdots ,A_{(n)}]$$

（即各行排成的一列），亦可写成以列为元素的矩阵：

$$A=(A^{(1)} ,A^{(2)} ,\cdots ,A^{(n)})$$

（即各列排成的一行）.我们约定，以后也可以将$n\times n$矩阵$A$的行和列称为$n$阶行列式$\vert a_{ij} \vert $的行和列.

根据定义，$\vert \vert =\det $（$\text{determinanat}$的缩写）是一个函数，它把方阵$A$对应到一个数$\vert A\vert =\det A$，我们的任务是研究当改变矩阵$A$的行和列时，这个函数如何变化，这里将行和列看作线性空间$\mathbb{R}^n$中的元素（向量）.如果需要，$\det A$可简记作$n$个变量的函数$\det [A_{(1)} ,\cdots ,A_{(n)}]$（见第$1$章$\S 5$第$2$段），或者$\det (A^{(1)} ,\cdots ,A^{(n)})$，变量是$\mathbb{R}^n$中的向量.

一个函数$\mathcal{D} :[A_{(1)} ,\cdots ,A_{(n)} ]\mapsto \mathcal{D} (A_{(1)} ,\cdots ,A_{(n)})$叫作多重线性的，如果它在每一个分量$A_{(i)}$上都是线性，也就是说

$$\begin{align} & \mathcal{D} (A_{(1)} ,\cdots ,\alpha A’_{(i)} +\beta A’’_{(i)} ,\cdots ,A_{(n)} ) \\ = & \alpha \mathcal{D} (A_{(1)} ,\cdots ,A’_{(i)} ,\cdots ,A_{(n)}) +\beta \mathcal{D} (A_{(1)} ,\cdots ,A’’_{(i)} ,\cdots ,A_{(n)}) \end{align} $$

（与第$2$章$\S 3$的第$1$段比较）.如果

$$\begin{align} & \mathcal{D} (A_{(1)} ,\cdots ,A_{(i)},A_{(i+1)} ,\cdots ,A_{(n)} ) \\ = & -\mathcal{D} (A_{(1)} ,\cdots ,A_{(i+1)},A_{(i)} ,\cdots ,A_{(n)}) ,1\leq i\leq n-1 \end{align} \label{4} \tag{4} $$

则称函数$\mathcal{D}$为斜对称的（见第$1$章$\S 8$第$4$段）.

注记1$\quad $从线性函数的定义（见第$2$章$\S 3(4)$）可知，函数$\mathcal{D}$是多重线性的，当且仅当对于固定的$A_{(1)} ,\cdots ,A_{(i-1)} ,A_{(i+1)} ,\cdots ,A_{(n)}$以及$A_{(i)} =X=(x_1 ,\cdots ,x_n )$，我们有

$$\mathcal{D} (A_{(1)} ,\cdots ,A_{(n)} )=\alpha_1 x_1 +\alpha _2 x_2 +\cdots +\alpha _n x_n ,$$

其中$\alpha _1 ,\cdots ,\alpha _n $是不依赖于$x_1 ,\cdots ,x_n $的纯量.

注记2$\quad $多重线性函数$\mathcal{D}$的斜对称性等价于$\mathcal{D}$满足关系式

$$\mathcal{D} (A_{(1)} ,\cdots ,A_{(i-1)} ,X,X,A_{(i+2)} ,\cdots ,A_{(n)})=0,1\leq i\leq n-1.\label{41} \tag{4′}$$

事实上，在$\eqref{4}$中取$A_{(i)} =A_{(i+1)} =X$，我们得到$\eqref{41}$，反之，取$X=A_{(i)} +A_{(i+1)}$，由于$\mathcal{D}$的多重线性性，$\eqref{41}$导出了关系式

$$\begin{align} & \mathcal{D} (\cdots ,A_{(i)} ,A_{(i)} ,\cdots )+\mathcal{D} (\cdots ,A_{(i+1)} ,A_{(i+1)} ,\cdots ) +\mathcal{D} (\cdots ,A_{(i)} ,A_{(i+1)} ,\cdots )+\mathcal{D} (\cdots ,A_{(i+1)} ,A_{(i)} ,\cdots ) \\ = & \mathcal{D} (\cdots ,A_{(i)} +A_{(i+1)} ,A_{(i)} +A_{(i+1)} ,\cdots ) =0\end{align} $$

式中的前两项为零（在$\eqref{41}$中分别取$X=A_{(i)}$和$X=A_{(i+1)}$即可），所以后两项的和为零，得到关系式$\eqref{4}$.

同样的定义和讨论亦适用于列向量函数$\mathcal{D} (A^{(1)} ,\cdots ,A^{(n)})$.更一般地，斜对称性条件$\eqref{4}$适用于任意函数$\mathcal{D} \colon M^n \to \mathbb{R}$，其中$M^n$是集合$M$的笛卡儿幂，我们再一次指出，根据第$1$章引理$2$，当交换两个自变量的位置时，斜对称函数变号.

注意到在公式$\eqref{3}$中，矩阵$A$的行与列的地位乍看起来是不平等的.但如果交换$A$的行和列，则有转置矩阵$\sideset{^t}{}A$（见第$2$章$\S 3$，第$3$段）.因而要进行一下两个值$\det A$和$\det \sideset{^t}{}A$的比较.答案由定理$1$给出.

定理1$\quad $任意方阵$A$及其转置$\sideset{^t}{}A$的行列式相等：

$$\det \sideset{^t}{}A =\det A.$$

证明$\quad $令$A=(a_{ij} ) ,\sideset{^t}{}A =(a’_{ij} )$，此处$a’_{ij} =a_{ji}$.并注意到对任意数码$k\in \lbrace 1,2,\cdots ,n\rbrace $和任意置换$\pi \in S_n ,k=\pi (\pi ^{-1} k)%]，我们发现乘积$a’_{1,\pi (1)} \cdots a’_{n,\pi (n)}$中的有序因子在置换$\pi ^{-1}$的作用下给出

$$a’_{\pi ^{-1} (1) ,\pi ^{-1} (\pi (1))} \cdots a’_{\pi ^{-1} (n) ,\pi ^{-1} (\pi (n))} =a’_{\pi ^{-1} (1) ,1} \cdots a’_{\pi ^{-1} (n) ,n} =a_{1\pi ^{-1} (1)} \cdots a_{n\pi ^{-1} (n)} .$$

如果再考虑到$\varepsilon _{\pi} =\varepsilon _{\pi ^{-1}}$，（事实上$\varepsilon _{\pi } \cdot \varepsilon _{\pi ^{-1}}=\varepsilon _{\pi \pi ^{-1}} =\varepsilon _e =1$），而$\lbrace \pi ^{-1} \vert \pi \in S_n \rbrace =\lbrace \pi \vert \pi \in S_n \rbrace =S_n $（因为$\pi \mapsto \pi^{-1}$是从$S_n $到自身的一个一一映射），那么根据公式$\eqref{3}$有

$$\begin{align} \det \sideset{^t}{}A = & \sum_{\pi \in S_n } \varepsilon _{\pi } a’_{1,\pi (1)} \cdots a’_{n,\pi (n)} \\ = & \sum_{\pi \in S_n } \varepsilon _{\pi ^{-1}} a’_{\pi^{-1} (1),1} \cdots a’_{\pi^{-1} (n),n} \\ = & \sum_{\sigma \in S_n } \varepsilon _{\sigma } a_{1,\sigma (1)} \cdots a_{n,\sigma (n)} \\ = & \det A.\end{align} $$

注记3$\quad $定理$1$的论断表明，如果行列式满足某种相对于行（或列）的性质，那么该性质相对于列（或行）也被满足.

定理2$\quad $定义在集合$M_n (\mathbb{R} )$上的函数$\det \colon A\mapsto \det A$具有下述性质.

$\text{D1} .\;\det A$是矩阵$A$的行的斜对称函数（即交换任意两行时，行列式变号）.

$\text{D2} .\;\det A$是矩阵$A$的行的多重线性函数（即矩阵$A$的行列式是它的任意一行$A_{(k)}$的元素的线性函数）.

$\text{D3} .\;\det E=1$.

证明$\quad \text{D1} .\quad $设$A’$是由$A$交换行$A_{(s)} ,A_{(t)}$得到的矩阵，也就是说$A’_{(s)} =A_{(t)}$，$A’_{(t)} =A_{(s)}$，$A’_{(i)} =A_{(i)}$若$i\neq s,t$.将任意置换$\pi \in S_n$写成$\pi =\sigma \tau$的形式，其中$\tau =(st)$是一个对换（见第$1$章$\S 8$第$3$段公式$(10′)$关于置换$R_{\tau }$的确定），我们有

$$\begin{align} \det A’ = & \sum_{\pi \in S_n } \varepsilon _{\pi } a’_{1,\pi (1)} \cdots a’_{n,\pi (n)} \\ = & \sum_{\sigma \in S_n } \varepsilon _{\sigma \tau } a’_{1,\sigma \tau (1)} \cdots a’_{s,\sigma \tau (s)} \cdots a’_{t,\sigma \tau (t)} \cdots a’_{n,\sigma \tau (n)} \\ = & \sum_{\sigma \in S_n } \varepsilon _{\sigma \tau } a’_{1,\sigma (1)} \cdots a’_{s,\sigma (t)} \cdots a’_{t,\sigma (s)} \cdots a’_{n,\sigma (n)} \\ = & \sum_{\sigma \in S_n } \varepsilon _{\sigma \tau } a_{1,\sigma (1)} \cdots a_{t,\sigma (t)} \cdots a_{s,\sigma (s)} \cdots a_{n,\sigma (n)} \\ = & -\sum_{\sigma \in S_n } \varepsilon _{\sigma } a_{1,\sigma (1)} \cdots a_{n,\sigma (n)} \\ = & -\det A .\end{align} $$

$\text{D2} .\quad $设$A=(a_{ij})$，并设$A_{(k)} =\lambda’ A’_{(k)} +\lambda’’ A’’_{(k)}$，其中撇号指出了辅助矩阵

$$A’=[A_{(1)} ,\cdots ,A_{(k-1)} ,A’_{(k)} ,A_{(k+1)} ,\cdots ,A_{(n)}],$$

$$A’’=[A_{(1)} ,\cdots ,A_{(k-1)} ,A’’_{(k)} ,A_{(k+1)} ,\cdots ,A_{(n)}].$$

根据条件

$$a_{kj} =\lambda’ a’_{kj} +\lambda’’ a’’_{kj} ,\quad j=1,2,\cdots ,n.$$

基于注记$1$，$\det A$关于第$k$行$A_{(k)}$的元素的线性可以给出下述论断.由定义

$$\begin{align} & \det [A_{(1)} ,\cdots ,A_{(k)} ,\cdots ,A_{(n)}] \\ = & \det A \\ = & \sum_{\sigma \in S_n } \varepsilon _{\sigma } a_{1,\sigma (1)} \cdots a_{k,\sigma (k)} \cdots a_{n,\sigma (n)} \\ = & \sum_{\sigma \in S_n} p_{\sigma} a_{k,\sigma (k)} ,\end{align} $$

其中$p_{\sigma } ,\sigma \in S_n$是系数，它不依赖于行$A_{(k)}$的元素.将脚标满足$\sigma (k) =j ,\sigma \in S_n$的$p_{\sigma }$合并同类项，并设$\alpha_j =\displaystyle \sum_{\sigma (k) =j} p_{\sigma }$，我们就得到了所需的线性

$$\det [\cdots ,A_{(k)} ,\cdots ] =\sum_{j=1}^n \alpha_j a_{kj} ,$$

$$\begin{align} & \det [\cdots ,\lambda’ A’_{(k)} +\lambda’’ A’’_{(k)} ,\cdots ] \\ = & \sum_{j=1}^n \alpha_j (\lambda’ a’_{kj} +\lambda’’ a’’_{kj} ) \\ = & \lambda’ \sum_{j=1}^n \alpha_j a’_{kj} +\lambda’’ \sum_{j=1}^n \alpha_j a’’_{kj} \\ = & \lambda’ \det [\cdots ,A’_{(k)} ,\cdots ] +\lambda’’ \det [\cdots ,A’’_{(k)} ,\cdots ].\end{align} $$

简言之：

$$\det A =\lambda’ \det A’ +\lambda’’ \det A’’ .$$

$\text{D3} .\quad $显然，$\det E =\displaystyle \sum_{\sigma \in S_n } \varepsilon _{\sigma } \delta _{1,\sigma (1)} \cdots \delta_{n,\sigma (n)} =\varepsilon _e \delta _{1,1} \cdots \delta _{n,n}=1$.

定理$2$蕴含着几个简单的结论，我们简述为行列式的性质，但我们将在更广泛的情况下，对具有性质$\text{D1} \sim \text{D2} $的任意函数$D\colon M_n (\mathbb{R} )\to \mathbb{R} $进行证明.

$\text{D4} .\quad $设$A\in M_n (\mathbb{R} ),\lambda \in \mathbb{R}$.则

$$\det \lambda A =\lambda ^n \det A.$$

证明$\quad $对下标为$1,2,\cdots $的行依次运用性质$\text{D2}$，我们有

$$\begin{align} & \mathcal{D} (\lambda A) \\ = & \mathcal{D} [\lambda A_{(1)} ,\lambda A_{(2)} ,\cdots ,\lambda A_{(n)}] \\ = & \lambda \mathcal{D} [A_{(1)} ,\lambda A_{(2)} ,\cdots ,\lambda A_{(n)}] \\ = & \lambda ^2 \mathcal{D} [A_{(1)} ,A_{(2)} ,\cdots ,\lambda A_{(n)}] \\ = & \cdots \\ = & \lambda ^n \mathcal{D} [A_{(1)} ,A_{(2)} ,\cdots ,A_{(n)}] \\ = & \lambda ^n \mathcal{D} (A).\end{align} $$

$\text{D5} .\quad $有一行为零的行列式等于$0$.

证明$\quad $设$A_{(k)} =(0,0,\cdots ,0)$，那么也有$2A_{(k)} =(0,0,\cdots ,0)$.根据$\text{D2}$，

$$\begin{align} & \mathcal{D} (A) \\ = & \mathcal{D} [A_{(1)} ,\cdots ,A_{(k)} ,\cdots ,\lambda A_{(n)}] \\ = & \mathcal{D} [A_{(1)} ,\cdots ,2A_{(k)} ,\cdots ,\lambda A_{(n)}] \\ = & 2\mathcal{D} [A_{(1)} ,\cdots ,A_{(k)} ,\cdots ,\lambda A_{(n)}] \\ = & 2\mathcal{D} (A), \end{align} $$

从而$\mathcal{D} (A)=0$.

$\text{D6} .\quad $如果在方阵$A$中有两行相同，则$A$的行列式等于$0$.

证明$\quad $取满足性质$\text{D1} \sim \text{D2}$的任意函数$\mathcal{D}$.在$A$中交换两个彼此相同的行$A_{(s)} ,A_{(t)}$，我们仍然得到矩阵$A$.另一方面，由于$\mathcal{D}$满足性质$\text{D1}$，$\mathcal{D} (A)$的值变号，这样$\mathcal{D} (A) =-\mathcal{D} (A)$，从而$2\mathcal{D} (A) =0$，$\mathcal{D} (A)=0$.

$\text{D7} .\quad $如果对行列式的行施行（Ⅱ）型初等变换，其值不变.

证明$\quad $考察施行一次初等变换的情况就足够了.设矩阵$A’$是由矩阵$A$的第$t$行乘以$\lambda $加到第$s$行上得到的.由于$\mathcal{D}$的性质$\text{D1}$和$\text{D6}$，我们有

$$\begin{align} & \mathcal{D} (A’) \\ = & \mathcal{D} (A_{(1)} ,\cdots ,A_{(s)} +\lambda A_{(t)} ,\cdots ,A_{(n)}) \\ = & \mathcal{D} (\cdots ,A_{(s)} ,\cdots )+\lambda \mathcal{D} (\cdots ,A_{(t)} ,\cdots ,A_{(t)},\cdots ) \\ = & \mathcal{D} (A_{(1)} ,\cdots ,A_{(n)} ) \\ = & \mathcal{D} (A) .\end{align} $$

注记4$\quad $上述证明说明，满足性质$\text{D1} \sim \text{D2}$的任意函数$\mathcal{D} \colon M_n (\mathbb{R} ) \to \mathbb{R}$亦满足性质$\text{D4} \sim \text{D7}$（将记号$\det $换成$\mathcal{D}$）.

命题1$\quad $设

$$\overline{A}=\begin{pmatrix} {\overline{a}}_{11} & {\overline{a}}_{12} & \cdots & {\overline{a}}_{1n} \\ 0 & {\overline{a}}_{22} & \cdots & {\overline{a}}_{2n} \\ \cdots & \cdots & \cdots & \cdots \\ 0 & 0 & \cdots & {\overline{a}}_{nn} \end{pmatrix} \label{5} \tag{5}$$

是一个$n$阶上三角矩阵，$E$是单位矩阵，且$\mathcal{D} \colon M_n (\mathbb{R} )\to \mathbb{R} $是满足性质$\text{D1} \sim \text{D2}$是任意函数.则

$$\mathcal{D}(\overline{A} )=\mathcal{D} (E){\overline{a}}_{11} {\overline{a}}_{22} \cdots {\overline{a}}_{nn} .$$

证明$\quad $根据注记$4$，我们可以运用性质$\text{D2}$和$\text{D7}$.根据$\text{D2}$，将${\overline{a}}_{nn}$称到符号$\mathcal{D}$外：

$$\mathcal{D} \overline{A}={\overline{a}}_{nn} \mathcal{D} (\begin{pmatrix} {\overline{a}}_{11} & \cdots & {\overline{a}}_{1,n-1} & {\overline{a}}_{1n} \\ \cdots & \cdots & \cdots & \cdots \\ 0 & \cdots & {\overline{a}}_{n-1,n-1} & {\overline{a}}_{n-1,1} \\ 0 & \cdots & 0 & 1 \end{pmatrix} ).$$

现在对$\overline{A}$施行（Ⅱ）型初等变换，从符号$\mathcal{D}$内矩阵的第$i$行减去最后一行与${\overline{a}}_{in}$的乘积.这时最后一列的元素变为零（除${\overline{a}}_{nn} =1$），而矩阵中所有其他的元素保持不变.对所得矩阵的倒数第二行施行同样的论证，等等.依序施行一次，元素${\overline{a}}_{ii} $提到符号$\mathcal{D}$之前，论证重新开始.施行$n$次之后，我们确定

$$\mathcal{D} \overline{A}={\overline{a}}_{nn} \cdots {\overline{a}}_{11} \cdot \mathcal{D} (\begin{pmatrix} 1 & \cdots & 0 \\ \cdots & \cdots & \cdots \\ 0 & \cdots & 1 \end{pmatrix} ),$$

即为所求.

推论$\quad $如果$\overline{A}$是形如$\eqref{5}$式的矩阵，则

$$\det \overline{A} ={\overline{a}}_{11} {\overline{a}}_{22} \cdots {\overline{a}}_{nn} .\label{6} \tag{6} $$

证明$\quad $因为$\det E=1$（性质$\text{D3}$），推论直接由命题$1$得到.

公式$\eqref{6}$也可以从后面更一般的结论得到.先给出下述

定义$\quad $从矩阵$A=(a_{ij})$中去掉第$i$行和第$j$列得到的矩阵的行列式记作$M_{ij}$，称为矩阵$A$的对应于元素$a_{ij}$的子式.数值$A_{ij} =(-1)^{i+j} M_{ij}$叫作元素$a_{ij}$的代数余子式.

命题2$\quad $若

$$A=\begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ 0 & a_{22} & \cdots & a_{2n} \\ \cdots & \cdots & \cdots & \cdots \\ 0 & a_{n2} & \cdots & a_{nn} \end{pmatrix} ,$$

则

$$\det A =a_{11} M_{11} =a_{11} A_{11} .$$

证明$\quad $因为$\det A =\det \sideset{^t}{}A$（定理$1$），又因为$a_{11}$是第一列$A^{(1)}$中唯一的非零元素，故当$\pi (1) \neq 1$时，$a_{\pi (1),1} =0$，且

$$\det A=\sum_{\pi \in S_n } \varepsilon _{\pi } a_{\pi (1) ,1} a_{\pi (2) ,2} \cdots a_{\pi (n),n} =\sum_{\pi \in S_n ,\pi (1)=1} \varepsilon _{\pi } a_{1,1} a_{\pi (2),2} \cdots a_{\pi (n),n} .$$

保留第$1$个元素$1$不动的置换$\pi \in S_n$的集合与作用在$\lbrace 2,3,\cdots ,n\rbrace $上的置换的集合$S_{n-1} $重合.这样，

$$\begin{align}\det A = & a_{11} \sum_{\sigma \in S_{n-1}} \varepsilon _{\sigma } a_{\sigma (2),2} \cdots a_{\sigma (n),n} \\ = & a_{11} \begin{vmatrix} a_{22} & \cdots & a_{2n} \\ \cdots & \cdots & \cdots \\ a_{n2} & \cdots & a_{nn} \end{vmatrix} =a_{11} M_{11} .\end{align} $$

将命题$2$应用于上三角矩阵$\overline{A} $，得到等式$\det \overline{A} ={\overline{a}}_{11} {\overline{M}}_{11}$，其中

$${\overline{M}}_{11} =\begin{vmatrix} {\overline{a}}_{22} & & \ast \\ & \ddots & \\ 0 & & {\overline{a}}_{nn} \end{vmatrix}$$

是阶数比$\det \overline{A}$少$1$的同类型的行列式.显然由归纳法可得公式$\eqref{6}$.

上述性质提供了较简单地计算$n$阶行列式的可能性.方法之一如下.将矩阵$A=(a_{ij})$用初等变换化为上三角形（见第$1$章$\S 3$）.得到了形如$\eqref{5}$的矩阵$\overline{A}$.假设在过程中完成了$q$次（Ⅰ）型初等变换和若干次（Ⅱ）型初等变换.由于后者不改变行列式的值（$\text{D7}$），而每一个（Ⅰ）型初等变换将行列式变号（乘以$(-1)$），故$\det \overline{A} =(-1)^q \det A$.由公式$\eqref{6}$，我们有

$$\det \overline{A} ={\overline{a}}_{11} {\overline{a}}_{22} \cdots {\overline{a}}_{nn} .$$

这时

$$\det A =(-1)^q{\overline{a}}_{11} {\overline{a}}_{22} \cdots {\overline{a}}_{nn} .\label{7} \tag{7} $$

得到计算$\det A$的一种公式.

现在我们来根据公式$\eqref{7}$说明行列式的性质$\text{D1} -\text{D3}$所起的作用.

定理3$\quad $设$\mathcal{D} \colon M_n (\mathbb{R} ) \to \mathbb{R}$是具有下列性质的函数：

$i)\;$当交换矩阵$A\in M_n (\mathbb{R} )$的任意相邻两行时，$\mathcal{D} (A)$变号；

$ii)\;\mathcal{D} (A)$是$A$的每一行的线性函数（换言之，$\mathcal{D}(A)$是矩阵的行的斜对称多重线性函数）.

则

$$\mathcal{D} (A)=\mathcal{D} (E) \cdot \det A.$$

证明$\quad $我们知道，性质$i)$等价于说，当交换任意两行时，即在任意（Ⅰ）型初等变换下，$\mathcal{D} (A)$变号.根据注记$4$，$\mathcal{D} (A) $具有性质$\text{D4} -\text{D7} $.特别地，$\mathcal{D} (A)$的值在矩阵$A$的行经过（Ⅱ）型初等变换后不变.

借助初等变换将矩阵$A$化为上三角形$\eqref{5}$，其中某些${\overline{a}}_{ii}$可能等于零.考虑到前面的事实，我们有公式（见$\eqref{7}$）

$$\det A = (-1)^q \det \overline{A} =(-1)^q {\overline{a}}_{11} {\overline{a}}_{22} \cdots {\overline{a}}_{nn} ,$$

$$\mathcal{D} (A) =(-1)^q \mathcal{D} (\overline{A} ),$$

其中$q$是从$A$到$\overline{A}$所做的（Ⅰ）型初等变换的个数.关系式$\mathcal{D} (A)=\mathcal{D} (E)\det A$现在可以直接从命题$1$得出.

由此可见，函数$\det $的性质$\text{D1} -\text{D3}$唯一地刻画了这个函数.基于这一理由，我们将它们列为行列式的基本性质.从一开始就把具有性质$\text{D1} -\text{D3}$的函数$\mathcal{D}$叫作行列式也是可以的，但在那种情况下就必须证明它的存在性.对于我们来说，存在性是由函数$\det $自身的构造——公式$\eqref{3}$保证了的.

考虑到定理$3$今后的应用，我们没有在定理的叙述中加入规范化条件$\mathcal{D} (E)=1.$

习题

$1.\;$将下述三个变量的斜对称函数$\Delta \colon \mathbb{R}^3 \to \mathbb{R} $

$$\Delta (x,y,z)=(y-x)(z-x)(y-z)$$

写成三阶行列式的形式.

解：

$$\Delta (x,y,z) =\begin{vmatrix} y-x & 0 & 0 \\ 0 & z-x & 0 \\ 0 & 0 & y-z \end{vmatrix}$$

另解：

$$\Delta (x,y,z) =\begin{vmatrix} -1 & -1 & -1 \\ -x & -y & -z \\ -x^2 & -y^2 & -z^2 \end{vmatrix}$$

思路来源于下节的范德蒙德行列式.

$2.\;$设$A=(a_{ij}),A’=(a’_{ij})$是两个$n\times n$矩阵，$\Delta ,\Delta’$是它们的行列式.在下述情况下比较$\Delta $和$\Delta’$：

$a)\;$$a’_{ij} =2^{i-j} a_{ij}$；

$b)\;$$a’_{ij} =a_{n+1-i,j}$；

$c)\;$$a’_{ij} =a_{n+1-i,n+1-j}$.

解：$a)\;$设

$$A=(a_{ij}) =\begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \cdots & \cdots & \cdots & \cdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{pmatrix} ,A’=(a’_{ij}) =\begin{pmatrix} 0 & 2^{-1}a_{12} & \cdots & 2^{1-n}a_{1n} \\ 2a_{21} & 0 & \cdots & 2^{2-n}a_{2n} \\ \cdots & \cdots & \cdots & \cdots \\ 2^{n-1}a_{n1} & 2^{n-2}a_{n2} & \cdots & 0 \end{pmatrix}.$$

$$\begin{align}\Delta -\Delta’ = & \sum_{\sigma \in S_n } \varepsilon _{\sigma } a_{1\sigma (1)} a_{2\sigma (2)} \cdots a_{n\sigma (n)} -\displaystyle \sum_{\sigma \in S_n } \varepsilon _{\sigma } 2^{1-\sigma (1)}a_{1\sigma (1)} 2^{2-\sigma (2)}a_{2\sigma (2)} \cdots 2^{n-\sigma (n)}a_{n\sigma (n)} \\ = & \sum_{\sigma \in S_n ,\sigma (i) =i} \varepsilon _{\sigma } a_{1\sigma (1)} a_{2\sigma (2)} \cdots a_{i\sigma (i)} \dots a_{n\sigma (n)}, \end{align} $$

即$\Delta -\Delta’$的差为所有包含$a_{ii}$的项的和，记为$\delta $.因此，当$\delta \geq 0$时，有$\Delta \geq \Delta’$.

当$\delta < 0$时，有$\Delta < \Delta’$.

$b)\;$设

$$A’=(a’_{ij}) =\begin{pmatrix} a_{n1} & a_{n2} & \cdots & a_{nn} \\ a_{n-1,1} & a_{n-1,2} & \cdots & a_{n-1,n} \\ \cdots & \cdots & \cdots & \cdots \\ a_{11} & a_{12} & \cdots & a_{1n} \end{pmatrix}.$$

若$n=2k$时，则分别交换第$1$行与第$n$行，第$2$行与第$n-1$行交换，$\cdots $，第$k$行与第$k+1$行交换，共交换$k$次，这时矩阵$A’$可化成矩阵$A$.于是$\Delta’=(-1)^k\Delta $.若$k$为奇数，则$\Delta’ < \Delta $.若$k$为偶数，则$\Delta’ =\Delta $.

当$n=2k+1$时，则分别交换第$1$行与第$n$行，第$2$行与$n-1$行交换，$\cdots $，第$k$行与第$k+2$行交换，其中第$k+1$不动，共交换$k$次，这时矩阵$A’$可化成矩阵$A$.于是$\Delta’ =(-1)^k \Delta $.若$k$为奇数，则$\Delta’ < \Delta $.若$k$为偶数，则$\Delta’ =\Delta $.

$c)\;$设

$$A’=(a’_{ij}) =\begin{pmatrix} a_{nn} & a_{n,n-1} & \cdots & a_{n1} \\ a_{n-1,n} & a_{n-1,n-1} & \cdots & a_{n-1,1} \\ \cdots & \cdots & \cdots & \cdots \\ a_{1n} & a_{1,n-1} & \cdots & a_{11} \end{pmatrix}.$$

若$n=2k$时，首先分别交换第$1$行与第$n$行，第$2$行与第$n-1$行交换，$\cdots $，第$k$行与第$k+1$行交换，共交换$k$次，这时矩阵$A’$可化成矩阵$A’’$，如下所示：

$$A’’=\begin{pmatrix} a_{1n} & a_{1,n-1} & \cdots & a_{11} \\ a_{2n} & a_{2,n-1} & \cdots & a_{2,1} \\ \cdots & \cdots & \cdots & \cdots \\ a_{nn} & a_{n,n-1} & \cdots & a_{n1} \end{pmatrix},$$

然后，分别交换第$1$列与第$n$列，第$2$列与第$n-1$列交换，$\cdots $，第$k$列与第$k+1$列交换，共交换$k$次，这时矩阵$A’’$可化成矩阵$A$.

于是$\Delta’=(-1)^k\Delta’’ =(-1)^{2k} \Delta $.知不论$k$为何数，必有$\Delta’ =\Delta $.

同理，若$n=2k+1$时，首先分别交换第$1$行与第$n$行，第$2$行与第$n-1$行交换，$\cdots $，第$k$行与第$k+2$行交换，共交换$k$次，这时矩阵$A’$可化成矩阵$A’’$，如下所示：

$$A’’=\begin{pmatrix} a_{1n} & a_{1,n-1} & \cdots & a_{11} \\ a_{2n} & a_{2,n-1} & \cdots & a_{2,1} \\ \cdots & \cdots & \cdots & \cdots \\ a_{nn} & a_{n,n-1} & \cdots & a_{n1} \end{pmatrix},$$

然后，分别交换第$1$列与第$n$列，第$2$列与第$n-1$列交换，$\cdots $，第$k$列与第$k+2$列交换，共交换$k$次，这时矩阵$A’’$可化成矩阵$A$.

于是$\Delta’=(-1)^k\Delta’’ =(-1)^{2k} \Delta $.知不论$k$为何数，必有$\Delta’ =\Delta $.

$3.\;$证明

$$\begin{vmatrix} 1 & 1 & 1 & \dots & 1 & 1 \\ 1 & 2 & 1 & \dots & 1 & 1 \\ 1 & 1 & 3 & \dots & 1 & 1 \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ 1 & 1 & 1 & \dots & n & 1 \\ 1 & 1 & 1 & \dots & 1 & n+1 \end{vmatrix} =n!.$$

证明：第$1$行乘以$-1$分别加到第$2$行，第$3$行，$\cdots $，第$n$行，得到

$$\begin{vmatrix} 1 & 1 & 1 & \dots & 1 & 1 \\ 1 & 2 & 1 & \dots & 1 & 1 \\ 1 & 1 & 3 & \dots & 1 & 1 \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ 1 & 1 & 1 & \dots & n & 1 \\ 1 & 1 & 1 & \dots & 1 & n+1 \end{vmatrix} =\begin{vmatrix} 1 & 1 & 1 & \dots & 1 & 1 \\ 0 & 1 & 0 & \dots & 0 & 0 \\ 0 & 0 & 2 & \dots & 0 & 0 \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ 0 & 0 & 0 & \dots & n-1 & 0 \\ 0 & 0 & 0 & \dots & 0 & n \end{vmatrix}=n!,$$

得证.