在许多应用中需要研究多项式的根的分布问题.在证明了代数基本定理以后，这个问题可以通过下面将要论述的辐角原理来解决.

给了多项式$f(z)$及复平面上的一个区域，需要知道多项式在这个区域里面的根的个数.

我们假定区域$D$是由一条封闭的曲线围住的（图$5.5$），并且在区域的边界上多项式$f(z)$没有根.

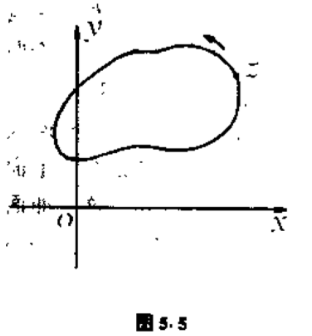
考虑两个辅助平面，一个是区域$D$所在的平面，称为$z$平面，另一个是$w$平面，并假定$w=f(z)$是这个平面上的点.当$z$在$z$平面上变化时，多项式的值$w=f(z)$就在$w$平面上变化.

设想点$z$沿区域$D$的边界上正向（使区域在边界的左边）通过一次，$f(z)$就在$w$平面上描出一条封闭的曲线（图$5.6$）.

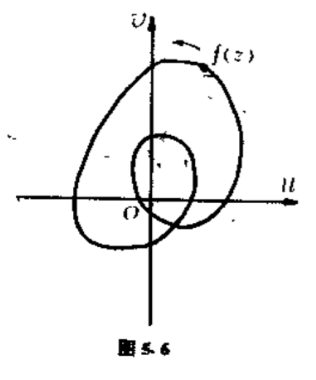
根据假设，$f(z)$在$D$的边界上任何一点都不为零，所以这条曲线不通过原点.

下面的定理给出了问题的解.

定理$1$（辐角原理）$\quad $设区域由一条闭曲线$C$所围成，假定多项式$f(z)$在$C$上没有零点，那么，$f(z)$在区域$D$内根的个数等于当$z$沿$C$的正方向通过一次时$f(z)$绕原点的圈数.

证明$\quad $设

$$f(z)=a_0 z^n +a_1 z^{n-1} +\cdots +a_n .$$

根据代数基本定理，$f(z)$可分解为一次因子的乘积

$$f(z)=a_0 (z-z_1 )(z-z_2 )\cdots (z-z_n ) ,$$

由复数乘积的辐角等于因子的辐角的和，我们有

$$\arg{f(z)} =\arg{a_0 } +\arg{(z-z_1 )} +\cdots +\arg{(z-z_n )} ,$$

用$\Delta \arg{f(z)}$表示$z$绕$C$的正方向环行一周时$f(z)$的辐角的改变量.易见，这个量是$2\pi $的整数倍.用$\Delta \arg{(z-z_i )}$表示$z$绕$C$的正方向环行一周时$\arg{(z-z_i )}$的改变量.于是我们有下述关系式：

$$\Delta \arg{f(z)} =\Delta \arg{a_0 } +\Delta \arg{(z-z_1 )} +\cdots +\Delta \arg{(z-z_n )} .$$

因为$a_0 $是一个常数，其辐角不会改变，所以$\Delta \arg{a_0 } =$.$z-z_1 $可以用从点$z_1 $到点$z$的向量来表示.若$z_1 $在$D$内部，从几何上看，当点$z$沿$C$绕行一周时，向量$z-z_1 $以$z_1 $为中心绕过一整周（图$5.7$），因此$\Delta \arg{(z-z_1 )} =2\pi $.

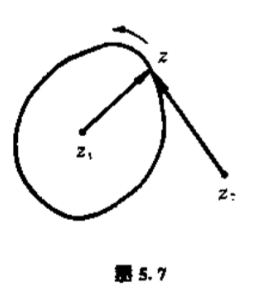
现在假定$z_2 $位于区域之外，在这种情况下，当$z$沿$C$绕行一周时，向量$z-z_2 $没有绕过$z_2 $，因此$\Delta \arg{(z-z_2 )} =0$.我们可以用这种方法考察$f(z)$的所有根.由此我们得出结论：$\Delta \arg{f(z)} $等于$2\pi $乘以$f(z)$在区域内的根的个数，因此$f(z)$位于区域内的根的个数等于点$f(z)$绕原点的次数.这就是要证明的.

通常我们并不直接用辐角原理来计算某区域内的多项式的根的个数，而借助下面的路西定理来计算.

定理$2$（路西定理）$\quad $设$P(z)$和$Q(z)$是两个多项式，$C$是一条闭曲线.若在$C$上$P(z)$和$Q(z)$满足$\vert P(z) \vert > \vert Q(z)\vert $，则在$C$的内部$P(z)+Q(z)$和$P(z)$有相同的零点个数.

证明$\quad $我们利用辐角原理来求$P(z)+Q(z)$的零点个数.在曲线$C$上将$P(z)+Q(z)$改写为

$$P(z)+Q(z)=P(z)\left[ 1+\dfrac{Q(z)}{P(z)} \right] .$$

注意，在曲线$C$上，$\vert P(z)\vert > \vert Q(z)\vert $，所以$P(z)$在$C$上不会为零，于是

$$\arg{[P(z)+Q(z)]} =\arg{P(z)} +\arg{\left[ 1+\dfrac{Q(z)}{P(z)} \right] } ,$$

但是$\left\vert \dfrac{Q(z)}{P(z)} \right\vert < 1$，所以向量$1+\dfrac{Q(z)}{P(z)} $的终点画出一条闭曲线，整个这条闭曲线都在以$1$为中心，以$1$为半径的圆内.因此这个向量没有绕原点转圈.于是当$z$绕行$C$一周后，$\arg{\left[ 1+\dfrac{Q(z)}{P(z)} \right] } $的值没有改变.所以

$$\Delta \arg{[P(z)+Q(z)]} =\Delta \arg{P(z)} ,$$

由辐角原理推出，$P(z)+Q(z)$和$P(z)$在$C$内有相同个数的根.

例$\quad $求在$\vert z\vert < 1$内方程

$$z^8 -4z^5 +z^2 -1=0$$

的根的个数.

解$\quad $我们利用路西定理.先将$z^8 -4^5+z^2 -1$表示成$P(z)+Q(z)$的形式，其中$P(z)=-4z^5$，$Q(z)=z^8+z^2-1$.在$\vert z\vert =1$上，

$$\vert Q(z)\vert =\vert z^8+z^2-1\vert \leqslant \vert z^8 \vert +\vert z^2\vert +1=3,$$

$$\vert P(z)\vert =\vert 4z^5 \vert =4,$$

所以

$$\vert Q(z)\vert < \vert P(z)\vert .$$

根据路西定理，$P(z)+Q(z)=z^8-4z^5 +z^2-1$在圆$\vert z\vert < 1$的零点个数与$P(z)=-4z^5$的零点个数相同.但$P(z)$在$\vert z\vert < 1$的零点个数是$5$，所以方程$z^8-4z^5+z^2 -1$在单位圆内的零点的个数也是$5$.