$1$.记号当$x\in X$时$\varphi (x)=O(\psi (x))$表示：存在常数$A$，使得当$x\in X$时

$$\vert \varphi (x)\vert \leqslant A\vert \psi (x)\vert .\label{1} \tag{1} $$

若在点$a(x\neq a)$的某个邻域$U_a $内不等式$\eqref{1}$成立，类似地可写出当$x\to a$时

$$\varphi (x)=O(\psi (x)).\label{2} \tag{2} $$

特别地，若当$x\in U_a (x\neq a)$时$\psi (x)\neq 0$，则只要存在有限的$\displaystyle \lim_{x\to a} \dfrac{\varphi (x)}{\psi (x)} \neq 0$，关系式$\eqref{2}$就显然成立.在这种情形下，我们写出

$$\varphi (x)=O^{\ast } (\psi (x)).$$

若

$$\lim_{x\to 0} \dfrac{\varphi (x)}{x^p} =k\neq 0(p > 0),$$

则称$\varphi (x)$为关于无穷小量$x$的$p$阶无穷小量.类似地，若

$$\lim_{x\to \infty } \dfrac{\psi (x)}{x^p} =k\neq 0(p > 0),$$

则称$\psi (x)$为关于无穷大量$x$的$p$阶无穷大量.

$2$.记号当$x\to a$时$\varphi (x)=o(\psi (x))$表示

$$\varphi (x)=\alpha (x)\psi (x)\quad (x\in U_a ,x\neq a),\label{3} \tag{3}$$

其中当$x\to a$时$\alpha (x)\to 0$.若当$x\in U_a ,x\neq a$时$\psi (x)\neq 0$，则等式$\eqref{3}$等价于

$$\lim_{x\to a} \dfrac{\varphi (x)}{\psi (x)} =0.$$

$3$.若当$x\to a$时

$$\varphi (x)-\psi (x)=o(\psi (x)),\label{4} \tag{4}$$

则称函数$\varphi (x)$与$\psi (x)$当$x\to a$时是等价的，即

$$\varphi (x)\sim \psi (x).$$

若当$x\in U_a ,x\neq a$时$\psi (x)\neq 0$，则由$\eqref{4}$有

$$\lim_{x\to a} \dfrac{\varphi (x)}{\psi (x)} =1.$$

当$x\to 0$时成立下列等价关系：

$$\sin{x} \sim x;\tan{x} \sim x;a^x -1\sim x\ln a(a > 0);$$

$$\ln (1+x)\sim x;\sqrt[n]{1+x} -1\sim \dfrac{x}{n} .$$

一般而言，$\varphi (x)+o(\varphi (x))\sim \varphi (x)$.

在计算当$x\to a$时两个无穷小（或无穷大）函数之比的极限时，可用等价函数所给函数.

内容简介$\quad $在这一节中对大$O$，小$o$，等价记号$\sim$等给出定义，并提出了等价量代换法.如前所说，这种方法的大量应用实例就是上一节的极限计算题.本节的习题数量很少，其中也只有最后一题（习题$661$）有一点困难，因此下面只举少量的例子来说明其中的问题.

在新版中增加了一个符号$O^{\ast}$，即当$x\in U_a (x\neq a)$时$\psi (x)\neq 0$，且存在有限的$\displaystyle \lim_{x\to a} \dfrac{\varphi (x)}{\psi (x)} \neq 0$时，记为

$$\varphi (x)=O^{\ast} (\psi (x))(x\to a).$$

与大$O$记号相比，在$\varphi (x)$与$\psi (x)$为关于$x\to a$的无穷小量（或无穷大量）时，$\varphi (x)=O^{\ast} (\psi (x))$表明二者为真正的同阶无穷小量（或无空大量），而$\varphi (x)=O(\psi (x))$只表明$\varphi (x)$的阶数不低于（不高于）$\psi (x)$的阶数.例如

$$x^3 =O(x^2)(x\to 0)$$

是正确的，但$x^3 =O^{\ast} (x^2)(x\to 0)$是错误的.同样，

$$x=O(x^2)(x\to +\infty )$$

是正确的，但$x=O^{\ast}(x^2)(x\to +\infty )$是错误的.

对于以下习题中将大$O$称为同阶都应当作以上理解.

此外，我们还经常用O(1)$代表（关于某种极限过程的）有界量，用$o(1)$代表无穷小量.这些记号中的大$O$与小$o$与一般的定义完全一致.

第一个习题用具体的几何图形给出了非常具体的无穷小量的例子，而且具有从一阶到三阶的不同阶数，这对于理解抽象的数学概念很有帮助.

$645$.认为圆心角$AOB=x$（图$4$）是$1$阶无穷小量，求下列各无穷小量的阶：

$(a)$弦$AB$；

$(b)$矢（拱高）$CD$；

$(c)$扇形$AOB$的面积；

$(d)$三角形$ABC$的面积；

$(e)$梯形$ABB_1 A_1 $的面积；

$(f)$弓形$ABC$的面积.

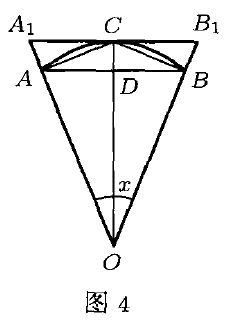
解$\quad $本题只要写出有关量的表达式后即可求出阶数，答案如下.（其中$R=OA=OC=OB$.）

$(a)$弦$AB=2R\sin{\dfrac{x}{2} } \sim Rx(x\to 0)$，为一阶无穷小量.

$(b)$矢$CD=R-R\cos{\dfrac{x}{2} } \sim R\cdot \dfrac{1}{2} \cdot \dfrac{x^2}{4} =\dfrac{R}{8} x^2 (x\to 0)$，为二阶无穷小量.

$(c)$扇形$AOB$的面积是$\dfrac{1}{2} R^2 x$，为一阶无穷小量.

$(d)$三角形$ABC$的面积等于三角形$OAC$和$OBC$的面积之和减去三角形$OAB$的面积，也等于弦$AB$乘矢$CD$除$2$：

$$\begin{align}
& 2\cdot \dfrac{1}{2} R^2 \sin{\dfrac{x}{2} } -\dfrac{1}{2} R^2 \sin{x} \\
= & R^2 \sin{\dfrac{x}{2} } -R^2 \sin{\dfrac{x}{2} } \cos{\dfrac{x}{2} } \\
= & R^2 \sin{\dfrac{x}{2} } \left( 1-\cos{\dfrac{x}{2} } \right) \\
\sim & \dfrac{R^2}{16} x^3 (x\to 0),
\end{align}$$

为三阶无穷小量.

$(e)$梯形$ABB_1 A_1 $的面积等于$\dfrac{1}{2} (AB+A_1 B_1 )\times CD$，即是

$$\dfrac{R}{2} (2\sin{\dfrac{x}{2} } +2\tan{\dfrac{x}{2} } )\cdot R(1-\cos{\dfrac{x}{2} } )\sim \dfrac{R^2}{8} x^3 (x\to 0),$$

为三阶无穷小量.

$(f)$弓形$ABC$的面积是$\dfrac{1}{2} R^2 x-\dfrac{1}{2} R^2 \sin{x} $，为三阶无穷小量.

这里可以利用在$\S 1.5$的命题$1.8(1)$中已经证明的不等式

$$0 < \dfrac{x-\sin{x}}{x^3} < \dfrac{1}{2} (0 < x < \dfrac{\pi }{2} ).$$

这样就已经有$x-\sin{x} =O(x^3)(x\to 0)$，即至少是不低于三阶的无穷小量.在今后我们将会证明有

$$\lim_{x\to 0} \dfrac{x-\sin{x}}{x^3} =\dfrac{1}{6} ,$$

从而就可以说，当$x\to 0$时$x-\sin{x} =O^{\ast} (x^3)(x\to 0)$，即恰好是三阶无穷小量.

下面对于等号两边出现大$O$和小$o$记号的等式作一点说明.这里要注意，它们不是普通的等式，而经常称为渐近等式，又将导出这类等式的分析称为渐近分析，因为它们反映的是在极限意义上的关系式.在一般情况下这类等式只能从左往右读，而不能反方向读.例如等式

$$o(1)=O(1)$$

的意思是：关于某个极限过程的无穷小量一定是有界量.这确实成立.关于数列这是收敛数列的有界性定理的特例，关于$x\to a$（设$a$为有限数）的极限过程，这就是函数于点$a$有极限则一定在该点的某个去心邻域上有界的特例.然而上述等式不能从右往左读，因为有界量当然不一定是无穷小量.

下面给出习题$646$中两个小题的解答.其中设$o(f(x))$是当$x\to a$时比函数$f(x)$有较低阶的任意无穷小量，而$O(f(x))$是当$x\to a$时与函数$f(x)(f(x) > 0)$同阶的无穷大量.此外为简明起见，总是假设分母上的函数非零.

$646$.设$o(f(x))$是当$x\to a$时比函数$f(x)$更低阶增长的任意函数，$O(f(x))$是当$x\to a$时与函数$f(x)$同阶增长的任意函数，其中$f(x) > 0$.证明：

$(a)o(o(f(x))) =o(f(x))$；

$(b)O(o(f(x)))=o(f(x))$；

$(c)o(O(f(x)))=o(f(x))$；

$(d)O(O(f(x)))=O(f(x))$；

$(e)O(f(x))+o(f(x))=O(f(x))$.

证$\quad (a)$因为

$$\lim_{x\to a} \dfrac{o(o(f(x)))}{f(x)} =\lim_{x\to a} \left\lbrace \dfrac{o(o(f(x)))}{o[f(x)]} \cdot \dfrac{o[f(x)]}{f(x)} \right\rbrace =0,$$

故$o(o(f(x))) =o(f(x))$.

$(b)$设$g(x)=o(f(x))$，即有$\displaystyle \lim_{x\to a} \dfrac{g(x)}{f(x)} =0$，又设$h(x)=O(g(x))$，即存在$M > 0$，$\delta > 0$，使得当$0 < \vert x-a\vert < \delta $时成立$\left\vert \dfrac{h(x)}{g(x)} \right\vert < M$.不妨设$\delta > 0$已经充分小，使得$f$在$0 < \vert x-a\vert < \delta $时有定义.

于是在$0 < \vert x-a\vert < \delta $时就可以如下估计

$$\left\vert \dfrac{h(x)}{f(x)} \right\vert =\left\vert \dfrac{h(x)}{g(x)} \right\vert \cdot \left\vert \dfrac{g(x)}{f(x)} \right\vert \leqslant M\cdot \left\vert \dfrac{g(x)}{f(x)} \right\vert \to 0(x\to a),$$

这就表明$h(x)=o(f(x))(x\to a)$.

$(c)$设$g(x)=O(f(x))$关于$x\to a$成立，即有$M > 0$和$\delta > 0$，使得当$0 < \vert x-a\vert < \delta $时有$\left\vert \dfrac{g(x)}{f(x)} \right\vert < M$，又设有$h(x)=o(g(x))(x\to a)$，即有$\dfrac{h(x)}{g(x)} \to 0 (x\to a)$.

于是在$0 < \vert x-a\vert < \delta $时可以估计如下：

$$\left\vert \dfrac{h(x)}{f(x)} \right\vert =\left\vert \dfrac{h(x)}{g(x)} \right\vert \cdot \left\vert \dfrac{g(x)}{f(x)} \right\vert \leqslant M\cdot \left\vert \dfrac{h(x)}{g(x)} \right\vert \to 0(x\to a),$$

这就是$h(x)=o(f(x))(x\to a)$.

注$\quad $虽然在习题$646$的题意中说明它是对无穷大量来讨论的，但从上面的证明可见这些等式对于无穷小量也同样成立.此外，这两个题最后都转化为有界量与无穷小量的乘积仍为无穷小量，即$O(1)\cdot o(1)=o(1)$.

$(d)$设$g(x)=O(f(x))$关于$x\to a$成立，即有$M > 0$和$\delta > 0$，使得当$0 < \vert x-a\vert < \delta $时有$\left\vert \dfrac{g(x)}{f(x)} \right\vert < M$，又设有$h(x)=O(g(x))(x\to a)$，即有$M’ > 0$，$\delta’ > 0$，使得当$0 < \vert x-a\vert < \delta’ $时，$\left\vert \dfrac{g(x)}{f(x)} \right\vert < M’(x\to a)$.

于是在$0 < \vert x-a\vert < \min{\lbrace \delta ,\delta’ \rbrace } $时可以估计如下：

$$\left\vert \dfrac{h(x)}{f(x)} \right\vert =\left\vert \dfrac{h(x)}{g(x)} \right\vert \cdot \left\vert \dfrac{g(x)}{f(x)} \right\vert \leqslant M\cdot M’ (x\to a),$$

这就是$h(x)=O(f(x))(x\to a)$.

$(e)$因为存在$M > 0$和$\delta > 0$，使得当$0 < \vert x-a\vert < \delta $时有

$$\left\vert \dfrac{O(f(x))+o(f(x))}{f(x)} \right\vert \leqslant \left\vert \dfrac{O(f(x))}{f(x)} \right\vert + \left\vert \dfrac{o(f(x))}{f(x)} \right\vert \to M (x\to a),$$

故$O(f(x))+o(f(x))=O(f(x))$.

$647$.设$x\to 0,n > 0$.证明：

$(a)CO(x^n )=O(x^n)$（$C\neq 0$为常数）；

$(b)O(x^n) +O(x^m)=O(x^n) (n > m)$；

$(c)O(x^n ) O(x^m )=O(x^{n+m}) $.

证$\quad (a)$设$g(x)=O(x^n)$关于$x\to 0$成立，即有$M > 0$和$\delta > 0$，使得当$0 < \vert x\vert < \delta $时有$\left\vert \dfrac{g(x)}{x^n} \right\vert < M$.

于是在$0 < \vert x\vert < \delta $时可以估计如下：

$$\left\vert \dfrac{Cg(x)}{x^n} \right\vert \leqslant \vert C\vert \cdot \left\vert \dfrac{g(x)}{x^n} \right\vert \to \vert C\vert \cdot M(x\to 0),$$

这就是$Cg(x)=O(x^n)(x\to 0)$.

$(b)$因为存在$M > 0$和$\delta > 0$，使得当$0 < \vert x\vert < \delta $时有

$$\left\vert \dfrac{O(x^n)+O(x^m)}{x^n} \right\vert \leqslant \left\vert \dfrac{O(x^n)}{x^n} \right\vert + \left\vert \dfrac{O(x^m)}{x^m} \cdot x^{m-n} \right\vert \to M (x\to 0),$$

故$O(x^n) +O(x^m)=O(x^n)$.

$(c)$因为存在$M > 0$和$\delta > 0$，使得当$0 < \vert x\vert < \delta $时有

$$\left\vert \dfrac{O(x^n)O(x^m)}{x^{n+m}} \right\vert \leqslant \left\vert \dfrac{O(x^n)}{x^n} \right\vert \cdot \left\vert \dfrac{O(x^m)}{x^m} \right\vert \to M^2 (x\to 0),$$

故$O(x^n ) O(x^m )=O(x^{n+m})$.

$648$.设$x\to +\infty ,n > 0$.证明：

$(a)CO(x^n )=O(x^n)$（$C\neq 0$为常数）；

$(b)O(x^n) +O(x^m)=O(x^n) (n > m)$；

$(c)O(x^n ) O(x^m )=O(x^{n+m}) $.

证$\quad (a)$设$g(x)=O(x^n)$关于$x\to +\infty $成立，即有$M > 0$和$N > 0$，使得当$x > N$时有$\left\vert \dfrac{g(x)}{x^n} \right\vert < M$.

于是在$x > N$时可以估计如下：

$$\left\vert \dfrac{Cg(x)}{x^n} \right\vert \leqslant \vert C\vert \cdot \left\vert \dfrac{g(x)}{x^n} \right\vert \to \vert C\vert \cdot M(x\to +\infty ),$$

这就是$Cg(x)=O(x^n)(x\to +\infty )$.

$(b)$因为存在$M > 0$和$N > 0$，使得当$x > N$时有

$$\left\vert \dfrac{O(x^n)+O(x^m)}{x^n} \right\vert \leqslant \left\vert \dfrac{O(x^n)}{x^n} \right\vert + \left\vert \dfrac{O(x^m)}{x^m} \cdot x^{m-n} \right\vert \to M (x\to +\infty ),$$

故$O(x^n) +O(x^m)=O(x^n)$.

$(c)$因为存在$M > 0$和$N > 0$，使得当$x > N$时有

$$\left\vert \dfrac{O(x^n)O(x^m)}{x^{n+m}} \right\vert \leqslant \left\vert \dfrac{O(x^n)}{x^n} \right\vert \cdot \left\vert \dfrac{O(x^m)}{x^m} \right\vert \to M^2 (x\to +\infty ),$$

故$O(x^n ) O(x^m )=O(x^{n+m})$.

$649$.证明符号$\sim $具有如下性质：

$(1)$自反性：$\varphi (x)\sim \varphi (x)$；

$(2)$对称性：若$\varphi (x)\sim \psi (x)$，则$\psi (x)\sim \varphi (x)$；

$(3)$传递性：若$\varphi (x)\sim \psi (x)$及$\psi (x)\sim \chi (x)$，则$\varphi (x)\sim \chi (x)$.

证$\quad (1)$因为$\dfrac{\varphi (x)}{\varphi (x)} \equiv 1\to 1$，所以，$\varphi (x)\sim \varphi (x)$.

$(2)$因为$\dfrac{\varphi (x)}{\psi (x)} \to 1$，所以，$\dfrac{\psi (x)}{\varphi (x)} \to 1$.即若$\varphi (x)\sim \psi (x)$，则$\psi (x)\sim \varphi (x)$.

$(3)$因为$\dfrac{\varphi (x)}{\psi (x)} \to 1$，$\dfrac{\psi (x)}{\chi (x)} \to 1$，所以，$\dfrac{\varphi (x)}{\chi (x)} = \dfrac{\varphi (x)}{\psi (x)} \cdot \dfrac{\psi (x)}{\chi (x)} \to 1$，即$\varphi (x)\sim \chi (x)$.

下面是关于一些具体函数的渐近分析，我们只对其中涉及对数函数的习题给出解答.

$650$.设$x\to 0$.证明下列等式：

$(a)2x-x^2=O(x)$；

$(b)x\sin{\sqrt{x}} =O(x^{\frac{3}{2} })$；

$(c)x\sin{\dfrac{1}{x} } =O(\vert x\vert )$；

$(d)\ln x=o(\dfrac{1}{x^{\varepsilon }} ) (\varepsilon > 0)$；

$(e)\sqrt{x+\sqrt{x+\sqrt{x}}} \sim \sqrt[8]{x} $；

$(f)\arctan{\dfrac{1}{x} } =O(1)$；

$(g)(1+x)^n=1+nx+o(x)$.

证明$\quad $由题设$x\to 0$，于是，

$(a)$因为$\dfrac{2x-x^2}{x} \to 2$，所以，$2x-x^2=O(x)$.

$(b)$因为$\dfrac{x\sin{\sqrt{x}}}{x\sqrt{x} } \to 1$，所以，$x\sin{\sqrt{x}} =O(x^{\frac{3}{2} })$.

$(c)$因为$\left\vert x\sin{\dfrac{1}{x} } \right\vert \leqslant \vert x\vert (x\neq 0)$，所以，$x\sin{\dfrac{1}{x} } =O(\vert x\vert )$.

$(d)$当$x\to +0$时$\ln x$和$\dfrac{1}{x^{\varepsilon }} $都是无穷大量.如果取这时的$\dfrac{1}{x}$为（标准的）一阶无穷大量，而称$\dfrac{1}{x^{\varepsilon }} =\left( \dfrac{1}{x} \right)^{\varepsilon }$为$\varepsilon $阶的无穷大量，则本题表明这时的$\ln x$的无穷大量的阶数一定低于任何正数$\varepsilon $.（但并不能对于$x\to +0 $时的无穷大量$\ln x$确定其阶数.）

令$t=-\ln x$，即有$x=e^{-t}$.于是有$x\to +0 \Leftrightarrow t\to +\infty $.于是就有

$$\dfrac{\ln x}{\dfrac{1}{x^{\varepsilon }}} =x^{\varepsilon } \ln x=-\dfrac{t}{(e^{\varepsilon })^t}=-\dfrac{t}{a^t} ,$$

其中$a=e^{\varepsilon } > 1$.下面只要用$\S 1.2.2$的习题$60$即可证明$\displaystyle \lim_{t\to +\infty } \dfrac{t}{a^t} =0$.

为此取$t$的整数部分$[t]$，则$[t]\leqslant t < [t]+1$，因此有

$$0 < \dfrac{t}{a^t} \leqslant \dfrac{[t]+1}{a^{[t]}} .$$

利用$\displaystyle \lim_{n\to \infty } \dfrac{n+1}{a^n} =0(a > 1)$，可见对任意的$\delta > 0$，存在$N$，当$n > N$时有$0 < \dfrac{n+1}{a^n} < \delta $.于是当$t\geqslant N$时也就有$0 < \dfrac{t}{a^t} < \delta $.这就证明了$\displaystyle \lim_{t\to +\infty } \dfrac{t}{a^t} =0$，也就是$\displaystyle \lim_{x\to +0} x^{\varepsilon } \ln x=0$.

注$1\quad $类似的习题在$\S 1.5$中有习题$591(b)$，其中$\varepsilon =1$.

注$2\quad $若观察这时的无穷小量$\dfrac{1}{\ln x}$与$x^{\varepsilon } (\varepsilon > 0)$的比较，则就得到习题$654$中的结论，即$\dfrac{1}{\ln x}$是比任何$x^{\varepsilon }(\varepsilon > 0)$还要低阶的无穷小量.

$(e)$因为$\displaystyle \lim_{x\to +0} \dfrac{\sqrt{x+\sqrt{x+\sqrt{x}}} }{x^{\frac{1}{8} }} =\lim_{x\to +0} \sqrt{x^{\frac{3}{4} } +\sqrt{x^{\frac{1}{2} } +1} } =1$，所以，$\sqrt{x+\sqrt{x+\sqrt{x}}} \sim \sqrt[8]{x} $.

$(f)$因为$\left\vert \arctan{\dfrac{1}{x} } \right\vert \leqslant \dfrac{\pi }{2} (x\neq 0)$，所以，$\arctan{\dfrac{1}{x} } =O(1)$.

$(g)$因为$\dfrac{(1+x)^n-1-nx}{x} =\dfrac{1}{2} n(n-1)x+\cdots \to 0$，所以，$(1+x)^n-1-nx=o(x)$，即$(1+x)^n=1+nx+o(x)$.

$651$.设$x\to +\infty $.证明下列等式：

$(a)2x^3-3x^2+1=O(x^3)$；

$(b)\dfrac{x+1}{x^2+1} =O(\dfrac{1}{x} )$；

$(c)x+x^2\sin{x} =O(x^2 )$；

$(d)\dfrac{\arctan{x} }{1+x^2} =O(\dfrac{1}{x^2} ) $；

$(e)\ln x=o(x^{\varepsilon })(\varepsilon > 0)$；

$(f)x^p e^{-x} =o(\dfrac{1}{x^2} )$；

$(g)\sqrt{x+\sqrt{x+\sqrt{x}} } \sim \sqrt{x} $；

$(h)x^2+x\ln^{100} x \sim x^2 $.

证：由题设$x\to +\infty $，于是，

$(a)$因为$\dfrac{2x^3-3x^2+1}{x^3} \to 2$，所以，$2x^3-3x^2+1=O(x^3)$.

$(b)$因为$\dfrac{\dfrac{x+1}{x^2+1} }{\dfrac{1}{x} } =\dfrac{x(x+1)}{x^2+1} \to 1$，所以，$\dfrac{x+1}{x^2+1} =O(\dfrac{1}{x} )$.

$(c)$因为$\left\vert \dfrac{x+x^2\sin{x} }{x^2} \right\vert =\left\vert \dfrac{1}{x} +\sin{x} \right\vert \leqslant 1 (x\to +\infty )$，所以，$x+x^2\sin{x} =O(x^2)$.

$(d)$因为$\dfrac{\dfrac{\arctan{x} }{1+x^2} }{\dfrac{1}{x^2} } =\dfrac{x^2\arctan{x} }{1+x^2} \to \dfrac{\pi }{2} $，所以，$\dfrac{\arctan{x} }{1+x^2} =O(\dfrac{1}{x^2} )$.

$(e)$当$x\to +\infty$时$\ln x$和$x^{\varepsilon }$都是正无穷大量.如果取这时的$x$为（标准的）一阶无穷大量，而称$x^{\varepsilon}$为$\varepsilon $阶的无穷大量，则本题表明，这时的$\ln x$的无穷大量的阶数一定低于任何正数$\varepsilon $.（但并不能对$x\to +\infty $时的无穷大量$\ln x$确定其阶数）.

令$\ln x=t$，则$x=e^t $，以下证明可模仿上题来做.或者也可以令$y=\dfrac{1}{x} $，于是有

$$\dfrac{\ln x}{x^{\varepsilon }} =-\dfrac{\ln y}{\dfrac{1}{y^{\varepsilon }} } ,$$

且$x\to +\infty \Leftrightarrow y\to +0$，因此问题已经归结为上题.

$(f)$因为$\dfrac{x^p e^{-x} }{\dfrac{1}{x^2} } =\dfrac{x^{p+2}}{e^x} \to 0 $，所以，$x^p e^{-x} =o(\dfrac{1}{x^2} )$.

$(g)$因为$\dfrac{\sqrt{x+\sqrt{x+\sqrt{x}} } }{\sqrt{x} } =\sqrt{1+\sqrt{\dfrac{1}{x} +\sqrt{\dfrac{1}{x^3} } } } \to 1 $，所以，$\sqrt{x+\sqrt{x+\sqrt{x}} } \sim \sqrt{x}$.

$(h)$因为$\dfrac{x^2+x\ln^{100} x }{x^2 } =1+\dfrac{\ln^{100} x}{x} \to 1 $，所以，$x^2+x\ln^{100} x \sim x^2 $.

$652.1$证明：当$x$充分大时，下面的不等式成立：

$(a)x^2+10x+100 < 0.001x^3$；

$(b)\ln^{1000} x < \sqrt{x} $；

$(c)x^{10} e^x < e^{2x} $.

证$\quad (a)$因为当$x\to +\infty $时，$\dfrac{x^2+10x+100 }{0.001x^3} \to 0$所以，当$x$充分大以后，有$\dfrac{x^2+10x+100 }{0.001x^3} < 1$，即

$$x^2+10x+100 < 0.001x^3.$$

$(b)$因为当$x\to +\infty $时，$\dfrac{\ln^{1000} x}{\sqrt{x} } \to 0$所以，当$x$充分大以后，有$\dfrac{\ln^{1000} x}{\sqrt{x} } < 1$，即

$$\ln^{1000} x < \sqrt{x} .$$

$(c)$因为当$x\to +\infty $时，$\dfrac{x^{10} e^x}{e^{2x} } =\dfrac{x^{10}}{e^x} \to 0$所以，当$x$充分大以后，有$\dfrac{x^{10} e^x}{e^{2x} } < 1$，即

$$x^{10} e^x < e^{2x} .$$

$652.2$证明渐近公式：当$x\to +\infty $时，

$$\sqrt{x^2+px+q} =x+\dfrac{p}{2} +O(\dfrac{1}{x} ).$$

证$\quad $因为当$x\to +\infty $时，

$$\begin{align}
& \dfrac{\sqrt{x^2+px+q} -x-\dfrac{p}{2} }{\dfrac{1}{x} } \\
= & \dfrac{x^2+px+q -(x+\dfrac{p}{2} )^2}{\dfrac{1}{x} (\sqrt{x^2+px+q} +x+\dfrac{p}{2})} \\
= & \dfrac{q-\dfrac{p^2}{4} }{\sqrt{1+\dfrac{p}{x} +\dfrac{q}{x^2} } +1+\dfrac{p}{2x} } \\
\to & q-\dfrac{p^2}{4} ,
\end{align}$$

所以，$\sqrt{x^2+px+q} =x+\dfrac{p}{2} +O(\dfrac{1}{x} )$.

习题$653$，$655-658$是一系列确定无穷小量和无穷大量的阶数及其主项的计算，它们完全依赖于$\S 1.5$中的极限计算.下面只举一个例子以说明如何解此类问题，它同时也是对于$\S 1.5$中有关极限计算的复习.

$653$.设$x\to 0$.分出下列函数的主部，其形式为$Cx^n $（$C$为常数），并求出它对无穷小量$x$的阶：

$(a)2x-3x^3+x^5$；

$(b)\sqrt{1+x} -\sqrt{1-x} $；

$(c)\sqrt{1-2x} -\sqrt[3]{1-3x} $；

$(d)\tan{x} -\sin{x} $.

解$\quad $所谓函数$f(x)$的主部$g(x)$，即满足

$$\dfrac{f(x)}{g(x)} \to 1$$

或$f(x)=g(x)+o(x)\quad (x\to 0)$.

$(a)$因为$\dfrac{2x-3x^3+x^5}{2x} \to 1(x\to 0)$，故其主部为$2x$，它对于无穷小量$x$是一阶的.

$(b)$因为$\dfrac{\sqrt{1+x} -\sqrt{1-x} }{x} =\dfrac{2}{\sqrt{1+x} +\sqrt{1-x} } \to 1(x\to 0)$，故其主部为$x$，它对于$x$是一阶的.

$(c)$利用$\S 1.5$中的命题$1.7$，即公式$(1.30’)$，就得到

$$(1-2x)^{\frac{1}{2} } =1-x-\dfrac{1}{8} (2x)^2 +o(x^2)=1-x-\dfrac{1}{2} x^2+o(x^2)(x\to 0),$$

$$(1-3x)^{\frac{1}{3} } =1-x-\dfrac{1}{9} (3x)^2 +o(x^2)=1-x- x^2+o(x^2)(x\to 0),$$

于是就得到

$$\begin{align}
& \lim_{x\to 0} \dfrac{f(x)}{x^2} \\
= & \lim_{x\to 0} \dfrac{\sqrt{1-2x} -\sqrt[3]{1-3x} }{x^2} \\
= & \lim_{x\to 0} \dfrac{[1-x-\dfrac{1}{2} x^2+o(x^2)]-[1-x- x^2+o(x^2)]}{x^2} \\
= & \dfrac{1}{2} ,
\end{align}$$

即得到$f(x)\sim \dfrac{1}{2} x^2(x\to 0)$，它在$x\to 0$时是二阶无穷小量.

注$\quad $从无穷小量的阶数分析就可以知道关键在于应用命题$1.7$写出二阶项，并由此知道$f(x)$为二阶无穷小量，从而只要计算$f(x)$除以$x^2$的极限即可求得主项.

当然如$\S 1.5.4$中关于无理函数的极限计算所说，这里也完全可以用初等代数来做，读者不妨一试.

$(d)$因为$\tan{x} -\sin{x} =\dfrac{2}{\cos{x} } \sin{x} \sin{}^2 \dfrac{x}{2} $，于是，$\dfrac{\tan{x} -\sin{x} }{\dfrac{x^3}{2} } \to 1(x\to 0)$，故其主部为$\dfrac{x^3}{2} $，它对于$x$是三阶的.

$654$.设$x\to 0$.证明：无穷小量

$$(a)f(x)=\dfrac{1}{\ln x} ;\quad (b)f(x)=e^{-\frac{1}{x^2} } $$

无论对任何的$n$，也无法与无穷小量$x^n (x > 0)$相比.即，对于任何的$n$，等式

$$\lim_{x\to 0} \dfrac{f(x)}{x^n} =k$$

都不成立，式中$k$为异于零的有限量.

证$\quad (a)$因为$\displaystyle \lim_{x\to +0} x^n \ln x=0(n > 0)$，于是，

$$\lim_{x\to +0} \dfrac{\dfrac{1}{\ln x} }{x^n} =\infty ,$$

即$\dfrac{1}{\ln x}$不能与无穷小量$x^n $作比较$(x\to +0)$.

$(b)$因为$\displaystyle \lim_{x\to +0} \dfrac{e^{-\frac{1}{x^2} } }{x^n} =0(n > 0)$，所以，$e^{-\frac{1}{x^2} } $不能与无穷小量$x^n$相比较$(x\to 0)$.

$655$.设$x\to 1$.分出下列函数的主部，其形式为$C(x-1)^n$，并求出它对无穷小量$x-1$的阶：

$(a)x^3-3x+2$；

$(b)\sqrt[3]{1-\sqrt{x} } $；

$(c)\ln x$；

$(d)e^x-e$；

$(e)x^x-1$.

解$\quad (a)$因为$x^3-3x+2 =(x-1)^2(x+2)$，又

$$\dfrac{x^3-3x+2}{3(x-1)^2} \to 1(x\to 1),$$

故其主部为$3(x-1)^2$，它对于$(x-1)$是二阶无穷小.

$(b)$因为$\sqrt[3]{1-\sqrt{x} } =-\dfrac{\sqrt[3]{x-1} }{\sqrt[3]{1+\sqrt{x} } } $，又

$$\dfrac{\sqrt[3]{1-\sqrt{x} } }{-\dfrac{\sqrt[3]{x-1} }{\sqrt[3]{2} } } \to 1(x\to 1),$$

故其主部为$-\dfrac{\sqrt[3]{x-1} }{\sqrt[3]{2} } $，它对于$(x-1)$是$\dfrac{1}{3}$阶无穷小.

$(c)$因为$\dfrac{\ln x}{x-1} =\dfrac{\ln [1+(x-1)]}{x-1} \to 1(x\to 1)$，

故其主部为$x-1$，它对于$(x-1)$是一阶无穷小.

$(d)$因为$e^x-e= e(e^{x-1} -1)$，又

$$\dfrac{e^{x-1} -1}{x-1} \to 1(x\to 1),$$

故其主部为$e(x-1)$，它对于$(x-1)$是一阶无穷小.

$(e)$因为$x^x-1= e^{x\ln x} -1$，又

$$\dfrac{e^{x\ln x} -1}{x-1} =\dfrac{e^{x\ln x} -1}{x\ln x} \cdot \dfrac{x\ln [1+(x-1)]}{x-1} \to 1(x\to 1),$$

故其主部为$x-1$，它对于$(x-1)$是一阶无穷小.

$655$.设$x\to +\infty $.分出下列函数的主部，其形式为$Cx^n $，并求出它对无穷大量$x$的阶：

$(a)x^2+100x+10000$；

$(b)\dfrac{2x^5}{x^3-3x+1} $；

$(c)\sqrt[3]{x^2-x} +\sqrt{x} $；

$(d)\sqrt{1+\sqrt{1+\sqrt{x}}} $.

解$\quad (a)$因为$x^2+100x+10000\sim x^2 (x\to +\infty )$，故其主部为$x^2$，它对于无穷大量$x$是二阶的.

$(b)$因为$\dfrac{\dfrac{2x^5}{x^3-3x+1} }{2x^2} =\dfrac{2x^5}{2x^5-6x^3+2x^2} \to 1(x\to +\infty )$，故其主部为$2x^2$，它对于无穷大量$x$是二阶的.

$(c)\sqrt[3]{x^2-x} +\sqrt{x} =x^{\frac{2}{3} } \left( \sqrt[3]{1-\dfrac{1}{x} } +\sqrt[6]{\dfrac{1}{x} } \right) $，于是，$\dfrac{\sqrt[3]{x^2-x} +\sqrt{x} }{x^{\frac{2}{3} } } =\sqrt[3]{1-\dfrac{1}{x} } +\sqrt[6]{\dfrac{1}{x} } \to 1(x\to +\infty )$，故其主部为$x^{\frac{2}{3} }$，它对于无穷大量$x$是$\dfrac{2}{3}$阶的.

$(d)$因为$\dfrac{\sqrt{1+\sqrt{1+\sqrt{x}}} }{\sqrt[8]{x} } \to 1(x\to +\infty )$，故其主部为$\sqrt[8]{x} $，它对于无穷大量$x$是$\dfrac{1}{8}$阶的.

$657$.设$x\to +\infty $.分出下列函数的主部，其形式为$C\left( \dfrac{1}{x} \right)^n $，并求出它对无穷小量$\dfrac{1}{x} $的阶：

$(a)\dfrac{x+1}{x^4+1} $；

$(b)\sqrt{x+1} -\sqrt{x} $；

$(c)\sqrt{x+2} -2\sqrt{x+1} +\sqrt{x} $；

$(d)\dfrac{1}{x} \sin{\dfrac{1}{x} } $.

解$\quad (a)$因为$\dfrac{\dfrac{x+1}{x^4+1} }{\left( \dfrac{1}{x} \right)^3 } =\dfrac{x^3(x+1)}{x^4} \to 1(x\to +\infty )$，故其主部为$\left( \dfrac{1}{x} \right)^3 $，它对于无穷大量$\dfrac{1}{x} $是$3$阶的.

$(b)$因为$\dfrac{\sqrt{x+1} -\sqrt{x} }{\dfrac{1}{2\sqrt{x}} } =\dfrac{2\sqrt{x} }{\sqrt{x+1} +\sqrt{x} } \to 1(x\to +\infty )$，故其主部为$\dfrac{1}{2} \left( \dfrac{1}{x} \right)^{\frac{1}{2} } $，它对于无穷大量$\dfrac{1}{x} $是$\dfrac{1}{2} $阶的.

$(c)$

$$\begin{align}
& \sqrt{x+2} -2\sqrt{x+1} +\sqrt{x} \\
= & \dfrac{2\sqrt{x(x+2)} -2(x+1)}{\sqrt{x+2} +\sqrt{x} +2\sqrt{x+1} } \\
= & \dfrac{-2}{\left( \sqrt{x+2} +\sqrt{x} +2\sqrt{x+1} \right) \left( \sqrt{x(x+2)} +x+1\right) } .
\end{align}$$

于是，由此得

$$\begin{align}
& \dfrac{\sqrt{x+2} -2\sqrt{x+1} +\sqrt{x} }{-\dfrac{1}{4} \left( \dfrac{1}{x} \right)^{\frac{3}{2} } } \\
= & \dfrac{8}{\left( \sqrt{1+\dfrac{2}{x} } +1+2\sqrt{1+\dfrac{1}{x} } \right) \left( \sqrt{1+\dfrac{2}{x} } +1+\dfrac{1}{x} \right) } \\
\to & 1(x\to +\infty ),
\end{align}$$

故其主部为$-\dfrac{1}{4} \left( \dfrac{1}{x} \right)^{\frac{3}{2} } $，它对于无穷大量$\dfrac{1}{x} $是$\dfrac{3}{2} $阶的.

$(d)$因为$\dfrac{\dfrac{1}{x} \sin{\dfrac{1}{x} } }{\dfrac{1}{x^2} } =\dfrac{\sin{\dfrac{1}{x} } }{\dfrac{1}{x} } \to 1(x\to +\infty )$，故其主部为$\left( \dfrac{1}{x} \right)^2 $，它对于无穷大量$\dfrac{1}{x} $是$2$阶的.

$658$.设$x\to 1$.分出下列函数的主部，其形式为$C\left( \dfrac{1}{x-1} \right)^n $，并求它对无穷大量$\dfrac{1}{x-1} $的阶：

$(a)\dfrac{x^2}{x^2-1}$；

$(b)\sqrt{\dfrac{1+x}{1-x} } $；

$(c)\dfrac{x}{\sqrt[3]{1-x^3}} $；

$(d)\dfrac{1}{\sin{\pi x}} $；

$(e)\dfrac{\ln x}{(1-x)^2} $.

解$\quad (a)\dfrac{x^2}{x^2-1} =\dfrac{x^2}{(x-1)(x+1)} $，于是，

$$\dfrac{\dfrac{x^2}{x^2-1} }{\dfrac{1}{2(x-1)} } = \dfrac{2x^2}{x+1} \to 1 (x\to 1),$$

故其主部为$\dfrac{1}{2(x-1)} $，它对于无穷大量$\dfrac{1}{x-1} $是一阶的.

$(b)$因为$\dfrac{\sqrt{\dfrac{1+x}{1-x} } }{\sqrt{2} \dfrac{1}{\sqrt{1-x} } } =\dfrac{\sqrt{1+x} }{\sqrt{2} } \to 1(x\to 1)$，故其主部为$\sqrt{2} \left( \dfrac{1}{1-x} \right)^{\frac{1}{2} } $，它对于无穷大量$\dfrac{1}{x-1} $是$\dfrac{1}{2} $阶的.

$(c)$因为$\dfrac{x}{\sqrt[3]{1-x^3}} =\dfrac{x}{\sqrt[3]{1-x}} \cdot \dfrac{1}{\sqrt[3]{1+x+x^2} } $，于是，

$$\dfrac{\dfrac{x}{\sqrt[3]{1-x^3}} }{\dfrac{1}{\sqrt[3]{3} \sqrt[3]{1-x} } } \to 1 (x\to 1),$$

故其主部为$\dfrac{1}{\sqrt[3]{3} } \left( \dfrac{1}{1-x }\right)^{\frac{1}{3} } $，它对于无穷大量$\dfrac{1}{x-1} $是$\dfrac{1}{3} $阶的.

$(d)$因为$\dfrac{\dfrac{1}{\sin{\pi x}} }{\dfrac{1}{\pi (1-x)} } =\dfrac{\pi (1-x) }{\sin{\pi (1-x)} } \to 1(x\to 1)$，故其主部为$\dfrac{1}{\pi } \left( \dfrac{1}{1-x} \right) $，它对于无穷大量$\dfrac{1}{x-1} $是一阶的.

$(e)$因为$\dfrac{\dfrac{\ln x}{(1-x)^2} }{\dfrac{1}{x-1} } =\dfrac{\ln [1+(x-1)] }{x-1} \to 1(x\to 1)$，故其主部为$\dfrac{1}{x-1} $，它对于无穷大量$\dfrac{1}{x-1} $是一阶的.

$659$.设$x\to +\infty ,f_n (x)=x^n (n=1,2,3,\cdots )$.证明：

$(1)$每一个函数$f_n (x)$都比其前面的一个函数$f_{n-1} (x)$增加得快；

$(2)$函数$e^x $比函数$f_n (x)(n=1,2,\cdots )$中的每一个都增加得快.

证$\quad (1)$因为$\dfrac{f_n (x)}{f_{n-1} (x)} =x\to +\infty $，所以，$f_n (x)$比$f_{n-1} (x)$增加较快.

$(2)$因为$\dfrac{e^x}{x^n} \to +\infty (x\to +\infty )$，$n$为任一固定的正整数，所以，$e^x$比$f_n (x)$中的每一个都增加得较快.

$660$.设$x\to +\infty ,f_n (x)=\sqrt[n]{x} (n=1,2,3,\cdots )$.证明：

$(1)$每一个函数$f_n (x)$都比其前面的一个函数$f_{n-1 } (x)$增加得慢；

$(2)$函数$f(x)=\ln x$比函数$f_n (x)(n=1,2,\cdots )$中的每一个都增加得慢.

证$\quad (1)$因为$\dfrac{f_n (x)}{f_{n-1} (x)} =x^{-\frac{1}{n(n-1)} } \to 0(x\to +\infty )$，所以，$f_n (x)$比$f_{n-1} (x)$增加得较慢.

$(2)$因为$\dfrac{\ln x}{\sqrt[n]{x} } \to 0(x\to +\infty )$，所以，$\ln x$比$f_n (x)$中的每一个增加得较慢.

下面是本节的最后一题.它表明，不存在增长速度最快的无穷大量.

$661$.证明：对于任意的函数序列

$$f_1 (x),f_2 (x),\cdots ,f_n (x),\cdots (x_0 < x < +\infty ),$$

可举出一函数$f(x)$，当$x\to +\infty $时它比函数$f_n (x)(n=1,2,\cdots )$中的每一个都增加得快.

解（分析法）$\quad $本题的目的是根据给定的函数序列$\lbrace f_n (x)\rbrace $构造一个函数$f(x)$，使得对于每一个$n$成立

$$\lim_{x\to +\infty } \left\vert \dfrac{f_n (x)}{f(x)} \right\vert =0.$$

可以设想，如果给定的是有限个函数$f_1 ,\cdots ,f_k $，那么只要简单地令

$$f(x)=x\cdot (\max{\lbrace \vert f_1 (x)\vert ,\cdots ,\vert f_k (x)\vert \rbrace } +1),$$

问题已经解决.（当然这时的方法很多，读者不妨自己考虑其他合乎要求的$f$.）

现在作一个跳跃，即对于给定的无限多个函数$\lbrace f_n \rbrace $，采用分段构造方法来定义合乎要求的$f$.为简明起见，不妨将题中的定义域改取为$[1,+\infty )$，然后定义

$$f(x)=n\cdot (\max{\lbrace \vert f_1 (x)\vert ,\cdots ,\vert f_n (x)\vert \rbrace } +1),n\leqslant x < n+1 (n=1,2,\cdots ).$$

于是其中的$n=[x]$，即自变量$x$的整数部分.

这时对于每一个$f_n (x)$，可以如下计算$f_n $与$f$之比的绝对值当$x\to +\infty $的极限.由于当$x > n$时有$[x] \geqslant n$，因此有$\vert f_n (x)\vert \leqslant \max{\lbrace \vert f_1 (x)\vert ,\cdots ,\vert f_{[x]} (x)\vert \rbrace }$，又利用$x-1 < [x]\leqslant x$，于是有

$$\left\vert \dfrac{f_n (x)}{f(x)} \right\vert =\dfrac{\vert f_n (x)\vert }{[x]\cdot (\max{\lbrace \vert f_1 (x)\vert ,\cdots ,\vert f_{[x]} (x)\vert \rbrace } +1)} < \dfrac{1}{[x]} < \dfrac{1}{x-1} ,$$

可见满足要求$\displaystyle \lim_{x\to +\infty } \left\vert \dfrac{f_n (x)}{f(x)} \right\vert =0$.

注$\quad $在$f$的定义中对于$\max{\lbrace \vert f_1 (x)\vert ,\cdots ,\vert f_{[x]} (x)\vert \rbrace } $还要加上$1$，这样可以保证对于任何$\lbrace f_n (x)\rbrace $，所构造的$f(x)$都满足$\displaystyle \lim_{x\to +\infty } f(x)=+\infty$.