低阶行列式

在介绍高斯方法时，我们没有过多地关注主未知数系数的值.那时着重关注于这些系数是非零的.现在我们进入消元法的精确步骤，尽管只是解低阶方形线性方程组.这样做将为我们提供一些思考的案例，以及在第三章给出的构造一般行列式理论的原始材料.

如$\S 3$所示，考虑带有两个未知数的两个方程

$$\begin{array}{c}
a_{11}x_1+a_{12}x_2=b_1, \\
a_{21}x_1+a_{22}x_2=b_2, \\
\end{array}\\ \tag{1}
$$

并试图寻找解的分量$x_1^0,x_2^0$的一般公式.

矩阵$
\begin{pmatrix}
a_{11} & a_{12} \\
a_{21} & a_{22} \\
\end{pmatrix}
$的行列式是一个表达式$a_{11}a_{22}-a_{21}a_{12}$，

记作

$$
\begin{vmatrix}
a_{11} & a_{12} \\
a_{21} & a_{22} \\
\end{vmatrix}
$$

这样对二阶方阵本身对应于一个数

$$
\begin{vmatrix}
a_{11} & a_{12} \\
a_{21} & a_{22} \\
\end{vmatrix}=a_{11}a_{22}-a_{21}a_{12}. \tag{2}
$$

如果我们希望从方程组$(1)$中消去$x_2$，则将第一个方程乘以$a_{22}$，第二个方程乘以$(-a_{12})$，然后相加，得到

$$
\begin{vmatrix}
a_{11} & a_{12} \\
a_{21} & a_{22} \\
\end{vmatrix}x_1=b_1a_{22}-b_2a_{12}.
$$

可以看到，方程的右边恰为矩阵$
\begin{pmatrix}
b_1 & a_{12} \\
b_2 & a_{22} \\
\end{pmatrix}
$的行列式.设$
\begin{vmatrix}
a_{11} & a_{12} \\
a_{21} & a_{22} \\
\end{vmatrix}\neq 0
$.于是我们有

$$
x_1=\dfrac{\begin{vmatrix}
b_1 & a_{12} \\
b_2 & a_{22} \\
\end{vmatrix}}{\begin{vmatrix}
a_{11} & a_{12} \\
a_{21} & a_{22} \\
\end{vmatrix}},
x_2=\dfrac{\begin{vmatrix}
a_{11} & b_1 \\
a_{12} & b_2 \\
\end{vmatrix}}{\begin{vmatrix}
a_{11} & a_{12} \\
a_{21} & a_{22} \\
\end{vmatrix}}.\tag{3}
$$

有了含两个未知数，两个方程的线性方程组的求解公式，我们也能够解某些其他的方程组了(解方程组——意味着找出它们的解).例如，我们考察含三个未知数，两个齐次方程的线性方程组

$$\begin{array}{c}
a_{11}x_1+a_{12}x_2+a_{13}x_3=0, \\
a_{21}x_1+a_{22}x_2+a_{23}x_3=0. \\
\end{array}\\ \tag{4}
$$

我们的兴趣在于找出这个方程组的非零解，即至少有一个$x_i \neq 0$的解.例如设$x_3 \neq 0$.用$x_3$去除方程的两端，并设$y_1 =-\dfrac{x_1}{x_3},y_2 =-\dfrac{x_2}{x_3}$，将方程组$(4)$写成$(1)$的形式

$$\begin{array}{c}
a_{11}y_1+a_{12}y_2=a_{13}, \\
a_{21}y_1+a_{22}y_2=a_{23} \\
\end{array}\\
$$

当行列式$
\begin{vmatrix}
a_{11} & a_{12} \\
a_{21} & a_{22} \\
\end{vmatrix}\neq 0
$时，公式$(3)$给出

$$
y_1=-\dfrac{x_1}{x_3}=\dfrac{\begin{vmatrix}
a_13 & a_{12} \\
a_23 & a_{22} \\
\end{vmatrix}}{\begin{vmatrix}
a_{11} & a_{12} \\
a_{21} & a_{22} \\
\end{vmatrix}},
y_2=-\dfrac{x_2}{x_3}=\dfrac{\begin{vmatrix}
a_{11} & a_13 \\
a_{21} & a_23 \\
\end{vmatrix}}{\begin{vmatrix}
a_{11} & a_{12} \\
a_{21} & a_{22} \\
\end{vmatrix}}.
$$

毫不奇怪，我们从方程组$(4)$出发得不到$x_1,x_2,x_3$本身，而只能得到它们的比:由方程组的齐次性易见，如果$(x_1^0,x_2^0,x_3^0)$是解，且$c$是任意常数，则$(cx_1^0,cx_2^0,cx_3^0)$也是解.所以我们可以从

$$
x_1=-\begin{vmatrix}
a_{13} & a_{12} \\
a_{23} & a_{22} \\
\end{vmatrix},
x_2=-\begin{vmatrix}
a_{11} & a_{13} \\
a_{21} & a_{23} \\
\end{vmatrix},
x_3=\begin{vmatrix}
a_{11} & a_{12} \\
a_{21} & a_{22} \\
\end{vmatrix} \tag{5}
$$

入手，方程组的任意解均可由对所有的$x_i$乘以某个常数$c$得到.为了具有更对称的答案，从公式$(2)$直接导出

$$
\begin{vmatrix}
a & b \\
c & d \\
\end{vmatrix}=-\begin{vmatrix}
b & a \\
d & c \\
\end{vmatrix}.
$$

因而$(5)$能够写成下述形式：

$$
x_1=\begin{vmatrix}
a_{12} & a_{13} \\
a_{22} & a_{23} \\
\end{vmatrix},
x_2=-\begin{vmatrix}
a_{11} & a_{13} \\
a_{21} & a_{23} \\
\end{vmatrix},
x_3=\begin{vmatrix}
a_{11} & a_{12} \\
a_{21} & a_{22} \\
\end{vmatrix}. \tag{6}
$$

这些公式是在$\begin{vmatrix}
a_{11} & a_{12} \\
a_{21} & a_{22} \\
\end{vmatrix}\neq 0
$的假设下推导出来的.不难验证，只要公式$(6)$任意一个行列式不等于零，所给的结论就是正确的.如果三个行列式都等于零，尽管公式$(6)$给出了一个零解，但我们不能断定所有的解都可以用它乘以一个常数得到(例如考虑由两个相同的方程$x_1+x_2+x_3=0$组成的方程组).

现在转到含三个未知数三个方程的方程组

$$\begin{array}{c}
a_{11}x_1+a_{12}x_2+a_{13}x_3=0, \\
a_{21}x_1+a_{22}x_2+a_{23}x_3=0, \\
a_{31}x_1+a_{32}x_2+a_{33}x_3=0. \\
\end{array}\\
$$

我们希望从这个方程组中消去$x_2$和$x_3$，以便得到$x_1$的值.为此将第一个方程乘以$c_1$，第二个方程乘以$c_2$，第三个方程乘以$c_3$，并将所得结果相加.然后选取$c_1,c_2,c_3$使得在所得方程中含$x_2$及$x_3$的项为零.令$x_2$和$x_3$的系数等于零，我们就得到了关于$c_1,c_2,c_3$的方程

$$a_{12}c_1+a_{22}c_2+a_{32}c_3=0,$$

$$a_{13}c_1+a_{23}c_2+a_{33}c_3=0,$$

与方程组$(4)$属同一类型.因而可取

$$
c_1=\begin{vmatrix}
a_{22} & a_{32} \\
a_{23} & a_{33} \\
\end{vmatrix},
c_2=-\begin{vmatrix}
a_{12} & a_{32} \\
a_{13} & a_{33} \\
\end{vmatrix},
c_3=\begin{vmatrix}
a_{12} & a_{22} \\
a_{13} & a_{23} \\
\end{vmatrix}.
$$

经过显然的替换之后，我们得到了关于$x_1$的表达式

$$\begin{array}{c}
(a_{11}\begin{vmatrix}
a_{22} & a_{23} \\
a_{32} & a_{33} \\
\end{vmatrix}
-a_{21}\begin{vmatrix}
a_{12} & a_{13} \\
a_{32} & a_{33} \\
\end{vmatrix}
+a_{31}\begin{vmatrix}
a_{12} & a_{13} \\
a_{22} & a_{23} \\
\end{vmatrix})x_1 \\
=b_1\begin{vmatrix}
a_{22} & a_{23} \\
a_{32} & a_{33} \\
\end{vmatrix}
-b_2\begin{vmatrix}
a_{12} & a_{13} \\
a_{32} & a_{33} \\
\end{vmatrix}
+b_3\begin{vmatrix}
a_{12} & a_{13} \\
a_{22} & a_{23} \\
\end{vmatrix})x_1 .\\ \tag{7}
\end{array}\\
$$

式中$x_1$的系数叫作矩阵

$$ \begin{pmatrix}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33} \\
\end{pmatrix}
$$

的行列式，并记作

$$ \begin{vmatrix}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33} \\
\end{vmatrix}
$$

这样我们就借助于二阶行列式给出了三阶行列式的表达式

$$ \begin{array}{c}
\begin{vmatrix}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33} \\
\end{vmatrix}
=a_{11}\begin{vmatrix}
a_{22} & a_{23} \\
a_{32} & a_{33} \\
\end{vmatrix}
-a_{21}\begin{vmatrix}
a_{12} & a_{13} \\
a_{32} & a_{33} \\
\end{vmatrix}
+a_{31}\begin{vmatrix}
a_{12} & a_{13} \\
a_{22} & a_{23} \\
\end{vmatrix} \\
=a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32}-a_{11}a_{23}a_{32}-a_{12}a_{21}a_{33}-a_{13}a_{22}a_{31}.\\
\tag{8}
\end{array}\\
$$

容易发现，等式$(7)$的右边是将$x_1$的系数$a_{11}$换成$b_1$，$a_{21}$换成$b_2$，$a_{31}$换成$b_3$得到的.所以$(7)$式可以写成

$$ \begin{vmatrix}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33} \\
\end{vmatrix}x_1=\begin{vmatrix}
b_1 & a_{12} & a_{13} \\
b_2 & a_{22} & a_{23} \\
b_3 & a_{32} & a_{33} \\
\end{vmatrix}
$$

设$x_1$的系数不等于零.这时通过对$x_2$，$x_3$的类似计算，我们可以得到表述$x_1$，$x_2$，$x_3$的下述公式

$$ x_1=\dfrac{\begin{vmatrix}
b_1 & a_{12} & a_{13} \\
b_2 & a_{22} & a_{23} \\
b_3 & a_{32} & a_{33} \\
\end{vmatrix}}{\begin{vmatrix}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33} \\
\end{vmatrix}},x_2=\dfrac{\begin{vmatrix}
a_{11} & b_1 & a_{13} \\
a_{21} & b_2 & a_{23} \\
a_{31} & b_3 & a_{33} \\
\end{vmatrix}}{\begin{vmatrix}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33} \\
\end{vmatrix}},
x_3=\dfrac{\begin{vmatrix}
a_{11} & a_{12} & b_1 \\
a_{21} & a_{22} & b_2 \\
a_{31} & a_{32} & b_3 \\
\end{vmatrix}}{\begin{vmatrix}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33} \\
\end{vmatrix}}.\tag{9}
$$

显然，同样的推理适用于四个，五个或更多的方程组成的方程组，只要未知数的个数与方程的个数相同.为此我们必须首先引出一个类似于$(6)$的公式，对含有四个未知数，三个方程的齐次线性方程组求解； 然后在含有四个未知数，四个方程的线性方程组消去$x_2$，$x_3$，$x_4$，为此用$c_1$，$c_2$，$c_3$，$c_4$分别去乘四个方程并将结果相加.我们从三个齐次方程的方程组中找到$c_i$($=1,2,3,4$)的值.

这样得到的$x_1$的系数叫作四阶行列式，它可以仿照$(8)$由三阶行列式表出.

经过对$x_2$，$x_3$，$x_4$的相同认证，我们找到类似于$(9)$的对$x_i$的公式.这一过程可以无限地进行下去.在数学中有广泛应用的数学归纳原理(见$\S 7$)确保我们总会达到目的.

习题

$1$.如果用下列直观的符号法则来描述三阶行列式展开式中出现的乘积，就容易记住公式$(8)$了.

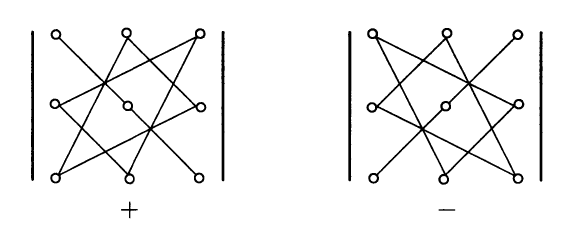
对四阶行列式可找到类似的法则.

解：先将$1$个四阶行列式写成$3$种不同形式，分别求出它们的值.

第$1$种形式：将第$1$，第$2$，第$3$列按顺序添加在第$4$列的后面.其中每列上方标注“$+$”和“$-$”分别表示该列按箭头方向$4$个元素乘积的符号.

$$\begin{array}{|cccc|ccc}
{+} & - & + & -/+ & - & + & - \\
a_{11} & a_{12} & a_{13} & a_{14} & a_{11} & a_{12} & a_{13}\\
a_{21} & a_{22} & a_{23} & a_{24} & a_{21} & a_{22} & a_{23}\\
a_{31} & a_{32} & a_{33} & a_{34} & a_{31} & a_{32} & a_{33}\\
a_{41} & a_{42} & a_{43} & a_{44} & a_{41} & a_{42} & a_{43}\\
\end{array} \\
=a_{11}a_{22}a_{33}a_{44}-a_{12}a_{23}a_{34}a_{41}+a_{13}a_{24}a_{31}a_{42}-a_{14}a_{21}a_{32}a_{43}+a_{14}a_{23}a_{32}a_{41}-a_{11}a_{24}a_{33}a_{42}+a_{12}a_{21}a_{34}a_{43}-a_{13}a_{22}a_{31}a_{44}
$$

第$2$种形式：将原四阶行列式的前$3$列进行一次轮换形成一个新的四阶行列式，再按第$1$种形式的方法计算.

$$\begin{array}{|cccc|ccc}
{+} & - & + & -/+ & - & + & - \\
a_{12} & a_{13} & a_{11} & a_{14} & a_{12} & a_{13} & a_{11}\\
a_{22} & a_{33} & a_{21} & a_{24} & a_{22} & a_{23} & a_{21}\\
a_{32} & a_{33} & a_{31} & a_{34} & a_{32} & a_{33} & a_{31}\\
a_{42} & a_{43} & a_{41} & a_{44} & a_{42} & a_{43} & a_{41}\\
\end{array}\\
=a_{12}a_{23}a_{31}a_{44}-a_{13}a_{21}a_{34}a_{42}+a_{11}a_{24}a_{32}a_{43}-a_{14}a_{22}a_{33}a_{41}+a_{14}a_{21}a_{33}a_{42}-a_{12}a_{24}a_{31}a_{43}+a_{13}a_{22}a_{34}a_{41}-a_{11}a_{23}a_{32}a_{44}
$$

第$3$种形式：将原四阶行列式的前$3$列进行二次轮换形成一个新的四阶行列式，再按第$1$种形式的方法计算.

$$\begin{array}{|cccc|ccc}
{+} & - & + & -/+ & - & + & - \\
a_{13} & a_{11} & a_{12} & a_{14} & a_{13} & a_{11} & a_{12}\\
a_{23} & a_{21} & a_{22} & a_{24} & a_{23} & a_{21} & a_{22}\\
a_{33} & a_{31} & a_{32} & a_{34} & a_{33} & a_{31} & a_{32}\\
a_{43} & a_{41} & a_{42} & a_{44} & a_{43} & a_{41} & a_{42}\\
\end{array}\\
=a_{13}a_{21}a_{32}a_{44}-a_{11}a_{22}a_{34}a_{43}+a_{12}a_{24}a_{33}a_{41}-a_{14}a_{22}a_{3}a_{42}+a_{14}a_{22}a_{31}a_{43}-a_{13}a_{24}a_{32}a_{41}+a_{11}a_{23}a_{34}a_{42}-a_{12}a_{21}a_{33}a_{44}
$$

综合分析上述$3$种形式的计算，不难发现原四阶行列式的值等于这$3$种形式计算结果之和.

$2$.证明在三阶行列式展开式中的六项不可能同时为正.

证明：由三阶行列式的表达式$(8)$可知，其展开式中的六项不可能同时为正.

$3$.验证

$$ \begin{vmatrix}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33} \\
\end{vmatrix}=\begin{vmatrix}
a_{11} & a_{21} & a_{31} \\
a_{12} & a_{22} & a_{32} \\
a_{13} & a_{23} & a_{33} \\
\end{vmatrix}，\begin{vmatrix}
0 & a & b \\
-a & 0 & c \\
-b & -c & 0 \\
\end{vmatrix}=0.$$

证明:由三阶行列式的表达式$(8)$可知，按其展开，可知上述两个等式成立.