在前两节中，我们遇到了各式各样的元素的集合，也遇到了集合之间的映射.例如给定的线性方程组的解的集合，或使每一个二阶矩阵对应于它的行列式的法则——都是某些形式概念的特例，了解形式概念(哪怕在直观的层面上)对今后的学习是非常有益的.

集合

集合指某些对象的总合，这些对象被称为元素.

含有有限个不同元素的集合可以用明确地列出全部元素的办法来描述，通常将这些元素写在花括号内.例如$\lbrace 1,2,4,8\rbrace $——从$1$到$10$之间$2$的方幂的集合.我们总是用某个字母表中的大写字母表示集合，用同一个或另一个字母表中的小写字母表示它的元素.

对于某些特殊重要的集合采用应当遵循的标准化记法.例如字母$\mathbb{N,Z,Q,R}$分别表示正整数(自然数)的集合，全体整数的集合，有理数集和实数集.

给定一个集合$S$，包含符号$a\in S$表明$a$是$S$的一个元素；反之，写$a\notin S$.

如果蕴含关系

$$\forall x,x\in S\Rightarrow x\in T$$

成立，则称$S$是$T$的一个子集，并记作$S\subset T$($S$包含在$T$中)(关于这一记法，请参考“给读者的建议”一节).

如果两个集合$S$与$T$有相同的元素，则称它们重合(或相等)，用符号的形式写成：

$$ S=T \Leftrightarrow S\subset T,T\subset S$$

($\Leftrightarrow$表示“当且仅当”或“双向蕴含”).

不包含任何元素的集合叫作空集，记作$\varnothing$，根据定义，空集是任意集合的子集.如果$S\subset T$，但$S\neq \varnothing$，且$S\neq T$，则$S$叫作$T$的真子集.为了区分出子集$S\subset T$，常常指明只有$S$中的元素才有的性质.例如

$$\lbrace n\in \mathbb{Z} \mid n=2m,m\in \mathbb{Z}\rbrace $$

是全体偶整数的集合，而

$$\mathbb{Z}=\lbrace n\in \mathbb{Z} \mid n > 0\rbrace $$

是自然数的集合.

两个集合$S$与$T$的交集是指集合

$$S\cap T=\lbrace x\mid x\in S且x\in T\rbrace ,$$

而并集指集合

$$S\cup T=\lbrace x\mid x\in S或x\in T\rbrace .$$

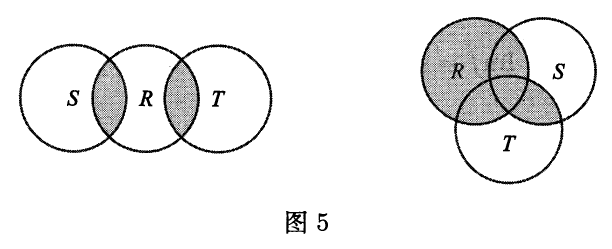
交集$S\cap T$可能是空集.这时称$S$和$T$是不相交的集合.交和并的运算满足恒等式

$$R\cap (S\cup T)=(R\cap S)\cup (R\cap T),$$

$$R\cup (S\cap T)=(R\cup S)\cap (R\cup T),$$

我们将这些式子的验证留作习题.图$5$有助于得出简单的论证.

两个集合$S$与$T$的差集$S \backslash T$指属于$S$但不属于$T$的元素的全体.在这里一般不假设$T\subset S$，有时也写$S-T$代替$S\backslash T$.

如果$T$是$S$的子集，也称$S\backslash T$为$T$在$S$中的补集.设$R=S\backslash T$，则$R\cap T=\varnothing$，$R\cup T=S$.注意集合的运算交、并、补与逻辑连词“且”、“或”、“非”之间存在着对应关系.

设$X,Y$是任意两个集合.任取$x\in X,y\in Y$，给定顺序的元素对$(x,y)$，叫作一个有序对，这时两个有序对$(x_1,y_1)=(x_2,y_2)$，当且仅当$x_1=x_2,y_1=y_2$.

全体有序对$(x,y)$的集合：

$$X\times Y=\lbrace (x,y)\mid x\in X,y\in Y\rbrace $$

叫作两个集合$X$和$Y$的笛卡儿积.

例如设$\mathbb{R}$是实数集.这时笛卡儿平方$\mathbb{R}^2=\mathbb{R} \times \mathbb{R}$就是在选定了坐标系的平面上点的笛卡儿坐标的集合.类似地，可以引出三个集合的笛卡尔积$X_1 \times X_2 \times X_3$($=(X_1 \times X_2)\times X_3=X_1 \times (X_2 \times X_3)$)，以及四个集合的笛卡儿积等等.

当$X_1 =X_2 =\cdots =X_k$时，简记作

$$X^k=X \times X \times \cdots \times X$$

并称之为集合$X$的$k$次笛卡儿方幂.$X^k$的元素是长为$k$的序列(或行)$(x_1 ,x_2 ,\cdots ,x_k)$.

为了区分集合$X\times Y$和$X\cup Y$，我们来看$X$和$Y$都具有有限基数($\text{cardinality}$)的情况：

$$\mid X\mid =\text{Card}X=n,\mid Y\mid=\text{Card}Y=m.$$

这时

$$\mid X\times Y \mid =n\cdot m,\mid X\cup Y\mid =n+m- \mid X\cap Y\mid .$$

如果还不清楚，请从头细读有关的定义.

映射

映射或函数的概念在数学中扮演着中心的角色.给定两个集合$X$和$Y$，以$X$为定义域，$Y$为值域的映射$f$将每个元素$x\in X$都对应于一个元素$f(x)\in Y$，$f(x)$亦可记作$fx$或$f_x$.当$X=Y$时，$f$也叫作集合$X$到自身的一个变换.用符号表示映射时写作$f:X\to Y$或$X\xrightarrow{f} Y$.

所有形如$f(x)$的元素的集合叫作映射$f$的像：

$$\text{Im}f=\lbrace f(x)\mid x\in X\rbrace =f(X)\subset Y$$

($\text{Im}$取自$\text{image}$(英文)).

集合

$$f^{-1}(y)=\lbrace x\in X \mid f(x)=y\rbrace $$

叫作元素$y\in Y$的原像.更一般地：对于$Y_0 \subset Y$，令

$$f^{-1}(Y_0 )=\lbrace x\in X\mid f(x)\in Y_0 \rbrace =\underset{y\in Y_0 }{\bigcup}f^{-1}(y).$$

如果$y\in Y\ \text{Im}f$，则显然有$f^{-1}(y)=\varnothing$.

设$f:X\to Y$是一个映射，如果$\text{Im}f=Y$，则称$f$为满射($\text{surjective}$(法文))或映上的；如果$x\neq x’$意味着$f(x)\neq f(x’)$，则称$f$为单射($\text{injective}$(法文)).最后，如果$f:X\to Y$既是满射又是单射，则称$f$为双射($\text{bijective}$(法文))或一一映射.

两个映射相等$f=g$，指它们有相同的定义域和值域：

$$X\xrightarrow{f} Y,X\xrightarrow{g} Y,$$

并且$\forall x\in X,f(x)=g(x)$，自变量$x$，即元素$x\in X$与其值$f(x)\in Y$的对应通常借助于一个短箭号表示出来：$x\mapsto f(x)$.

例如设$f_n$是第$n$个斐波那契数(见$\S 3$).则对应关系$n\mapsto f_n$定义了一个$\mathbb{N}\to \mathbb{N}$的映射，它既不是满射，也因为$f_1 =f_2$显然不是单射.再如若$\mathbb{R}_+$是正实数的集合，则由同一个规则$x\mapsto x^2$定义的映射

$$f: \mathbb{R}\to \mathbb{R},g:\mathbb{R}\to \mathbb{R}_+ \bigcup \lbrace 0\rbrace ,h:\mathbb{R}_+ \to \mathbb{R}_+$$

是彼此不同的：$f$既不满也不单，$g$是满射但不是单射，$h$是双射.由此看来，确定定义域和值域是定义一个映射(函数)的本质部分.

将每一个元素$x\in X$映到自身映射$e_x :X\to X$叫作单位映射（或恒等映射）.如果$X$是$Y$的子集：$X\subset Y$，有时定义五个专门的包含映射$I:X\to Y$是有益的，$I$将任意元素$x\in X$映到自身，但将后者看作是在集合$Y$中.映射$f:X\to Y$叫作映射$g:X’ \to Y’$的收缩(或限制)，如果$X\subset X’,Y\subset Y’$，且$\forall x\in X$，$f(x)=g(x)$.而$g$叫作映射$f$的扩张.例如嵌入映射$I:X\to Y$是恒等映射$e_y :Y\to Y$的限制.

我们也可以考虑多变元函数.集合$X$的笛卡儿方幂$X^n$的概念为我们提供了定义多变元函数$f(x_1 ,\cdots ,x_n )$的可能性，其中$x_i \in X$，$i=1,\cdots ,n$，这个函数就是一般的映射$f:X^n \to Y$.了解此点是有益处的.

设$g:U\to V,f:V\to W$是两个映射，由法则

$$(f\circ g)(u)=f(g(u))$$

定义的映射

$$f\circ g:U\to W$$

叫作$g$和$f$的乘积(叠加或合成).用下述三角图可以将$f\circ g$直观地描述出来：

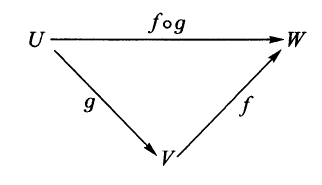
我们说这个图形可换(或是变换的)，即从$U$到$W$的结果不信赖于从$f\circ g$直接得到或通过中间阶段$V$得到.注意合成的定义不是对任意映射$f$和$g$都适用的.在上述记法中，它们必须有一个公共的集合$V$.但是集合$X$到自身的两个映射的合成永远有意义.

今后我们用简写$fg$代替$f\circ g$.任取映射$f:X\to Y$，我们有

$$fe_X =f,e_Y f=f.$$

这一性质的验证是显然的.合成(乘积)的一个重要性质表述如下.

定理$1$ 映射的合成满足结合律.也就是说，如果

$$h:U\to V,g:V\to W,f:W\to T$$

是三个映射，则

$$f(gh)=(fg)h.$$

证明 直观地讲，所有必要的论证包含在下图中：

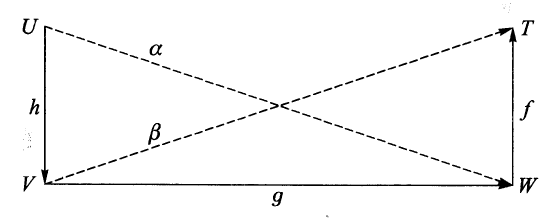
此处$\alpha =gh,\beta =fg$.根据映射相等的定义，需要比较映射$f(gh):U\to T$和$(fg)h:U\to T$在任意点$u\in U$的值.但按照映射合成的定义，我们有

$$(f(gh))(u)=f((gh)(u))=f(g(h(u)))=(fg)(h(u))=((fg)h)(u).\square$$

一般来说，集合$X$的映射的合成是不交换的，即$fg\neq gf$.这很容易从下例中看到，设$X=\lbrace a,b\rbrace $是两个元素的集合，令$f(a)=b$，$f(b)=a$，$g(a)=a$，$g(b)=a$.另一个例子：设$f$和$g$都是集合$X$的常值映射，即$f(x)$和$g(x)$不信赖于$x$的选取.则$f\neq g$意味着$fg\neq gf$.

某些映射有逆映射.设$f:X\to Y$，$g:Y\to X$是两个映射，则合成映射$fg$和$gf$是确定的.如果$fg=e_Y$，那么$f$叫作$g$的左逆，而$g$叫作$f$的右逆.当任意顺序的合成都是恒等映射，即：

$$fg=e_Y ,gf=e_X \tag{1}$$

时，则称$g$为$f$的双边逆(或简称逆)(而$f$也叫作$g$的逆)，并记作$f^{-1}$.这样，$f(u)=v\Leftrightarrow f^{-1}(v)=u$.

假设还存在着另一个映射$g’:Y\to X$，使得

$$fg’=e_Y ,g’f=e_X ,\tag{1′}$$

则根据等式$(1),(1’)$和定理$1$，我们得到

$$g’=e_X g’=(gf)g’=g(fg’)=ge_Y =g.$$

所以$f$的双边逆一旦存在，必定是唯一的.这也证实了符号$f^{-1}$的含意是明确的.

定理$2$ 映射$f:X\to Y$有逆，当且仅当$f$是双射.

证明 定理的证明信赖于下述引理，引理自身也是有趣的.

引理 设

$$f:X\to Y,g:Y\to X$$

是任意两个映射，如果$gf=e_X$，则$f$是单的，而$g$是满的.

证明 事实上，设$x,x’\in X$，且$f(x)=f(x’)$.则

$$x=e_X (x)=(gf)(x)=g(f(x))=g(f(x’))=(gf)(x’)=e_X (x’)=x’.$$

因此$f$是单射.如果给出$X$的任意元素$x$，则

$$x=e_X (x)=(gf)(x)=g(f(x)),$$

这就证明了$g$是满射.$\square$

回到定理$2$，先设$f$有逆映射$g=f^{-1}$.则等式$(1)$和引理给出了$f$的满单性.换言之，$f$是双射.反过来，设$f$是一个双射，则任取$y\in Y$，可以求出唯一的元素$x\in X$，使得$f(x)=y$.令$g(y)=x$，我们就定义了一个映射$g:Y\to X$，且$g$满足性质$(1)$.这就意味着$f^{-1}=g$.$\square$

推论 从双射$f:X\to Y$得到一个双射$f^{-1}$，且

$$(f^{-1})^{-1}=f.\tag{2}$$

设$f:X\to Y$，$h:Y\to Z$都是双射，则合成映射$hf$也是双射，并且

$$(hf)^{-1}=f^{-1}h^{-1}.\tag{3}$$

证明 根据定理$2$，$f$的双射性导出了$f^{-1}$的存在性.将条件$(1)$写成形式$ff^{-1}=_Y$，$f^{-1}f=e_X$，它的对称性给出了等式$(2)$.再根据定理$2$，$f^{-1}$也是双射.其次，由推论的条件和定理$2$，存在着映射

$$f^{-1}:Y\to X,h^{-1}:Z\to Y$$

及其合成

$$f^{-1}h^{-1}:Z\to X.$$

由等式

$$(hf)(f^{-1}h^{-1})=((hf)f^{-1})h^{-1}=(h(ff^{-1}))h^{-1}=hh^{-1}=e_Z ,$$

$$(f^{-1}h^{-1})(hf)=f^{-1}(h^{-1}(hf))=f^{-1}((h^{-1}h)f)=f^{-1}f=e_X ,$$

可以得到，$f^{-1}h^{-1}$是$fh$的逆映射.$\square$

由法则$\sigma (n)=n+1$定义的映射$\sigma :\mathbb{N} \to \mathbb{N}$是单射而不是满射，因为第一个元素$1$不属于$\text{Im}\sigma$.有趣的是对于有限集合，类似情况不会出现.

定理$3$ 如果$X$是有限集，且变换$f:X\to X$是单射，则$f$是双射.

证明 我们仅需指出$f$是满的，即对任意元素$x\in X$，找到$x’$，使得$f(x’)=x$.令

$$f^k(x)=f(f\cdots (f(x))\cdots )=f(f^{k-1}(x)),k=0,1,2,\cdots $$

由于$X$的有限性，在这一序列中必有重复的元素. 设$f^m(x)=f^n(x)$，$m>n$.若$n>0$，由等式$f(f^{m-1}(x))=f(f^{n-1}(x))$和$f$的单射性，得到$f^{m-1}(x)=f^{n-1}(x)$.

重复地消去$f$，经过足够多次，我们得到等式

$$f^{m-n}(x)=f^0(x)=e(x)=x.$$

这时取$x’=f^{m-n-1}(x)$，则$f(x’)=x$.$\square$

易见，有限集合到自身的一个满变换也是双射.

下面对基数谈几句.认为两个集合有相同的基数，当且仅当存在着双射$f:X\to Y$，与$\mathbb{N}$(或$\mathbb{Z}$)基数相同的集合叫作可数集.

习题

$1$.设$\Omega=\lbrace +,-,++,+-,-+,–,+++,\cdots \rbrace $是加号与减号的有限序列的集合，而$f:\Omega \to \Omega$是一个变换，将元素$\omega =\omega _1 \omega _2 \cdots \omega _n \in \Omega $对应到$\omega’=\omega _1 \dot{\omega _1} \omega _2 \dot{\omega _2} \cdots \omega _n \dot{\omega _n}$，其中若$\omega _k =+$，则$\dot{\omega _k}=-$，若$\omega _k =-$，则$\dot{\omega _k}=+$.证明在$f(f\omega )$的长度$>4$的任意区间内包含$++$或$–$.

证明：由题意，$f:\Omega \to \Omega$是一个变换，

$$f\omega =f(\omega _1 \omega _2 \cdots \omega _n )=\omega _1 \dot{\omega _1} \omega _2 \dot{\omega _2} \cdots \omega _n \dot{\omega _n} ,$$

$$f(f\omega )=f(\omega _1 \dot{\omega _1} \omega _2 \dot{\omega _2} \cdots \omega _n \dot{\omega _n} )= \omega _1 \dot{\omega _1} \dot{\omega _1} \dot{\dot{\omega _1} }\omega _2 \dot{\omega _2} \dot{\omega _2} \dot{\dot{\omega _2}} \cdots \omega _n \dot{\omega _n} \dot{\omega _n} \dot{\dot{\omega _n}} ,$$

一般地，对于任意的$k$，若$\omega _k =+$，则$\dot{\omega _n} =-,\dot{\dot{\omega _n}} =+$；若$\omega _k =-$，则$\dot{\omega _n} =+,\dot{\dot{\omega _n}} =-$.

因此，对于任意的$k$来说，$f(f\omega )$的某两相邻段$\omega _k \dot{\omega _k} \dot{\omega _k} \dot{\dot{\omega _k}} \omega _{k+1} \dot{\omega _{k+1}} \dot{\omega _{k+1}} \dot{\dot{\omega _{k+1}}} $必定是如下：

$$\begin{matrix} +-\,-++-\,-+ ,& +-\,-+-++-, \\ -++-\,-++-, & -++-+-\,-+ \end{matrix} $$

的某一形式.

但不论是哪种形式，对于长度$> 4$的任意区间段来说，其必定包含$++$或$-\,-$.

$2$.由法则$n\to n^2$给出的映射$f:\mathbb{N} \to \mathbb{N}$有右逆吗？给出$f$的两个左逆.

解：由法则$n\to n^2$给出的映射$f:\mathbb{N} \to \mathbb{N}$有右逆.由定义知,如果$fg=e_Y$，那么$g$叫作$f$的右逆.因此，定义一个由法则$n^2 \to n$给出的映射$g:\mathbb{N} \to \mathbb{N}$即可.这时所定义的映射$g$也是$f$的左逆.

另一个左逆$h$，可如下定义.先把映射$f$延拓到连续的实数集上成$f_R$，可定义实数集上的连续函数$h_R =\dfrac{f’_R }{2}$，这样把实数集上的连续函数$h_R$限制在自然数为平方数的子集上得到映射$h$，此即为左逆.

$3$.设$f:X\to Y$是一个映射，且$S,T$都是$X$的子集.

证明

$$f(S\cup T)=f(S)\cup f(T),f(S\cap T)\subset f(S)\cap f(T).$$

试举一例，说明后一个式子中的包含关系一般来说不能换成相等关系.

证明：$(1)$对于任意的$x\in S \cup T$来说，即$x\in S$或是$x\in T$，有$f(x)\in f(S)$或者$f(x)\in f(T)$成立，于是

$$f(x)\in f(S)\cup f(T),$$

故

$$f(S\cup T)\subset f(S)\cup f(T).$$

另一方面，因为$S\subset S\cup T$成立，故有$f(S)\subset f(S\cup T)$.同理有$T\subset S\cup T$成立，故有$f(T)\subset f(S\cup T)$.因此$f(S)\subset f(S\cup T)$或是$f(T)\subset f(S\cup T)$，故

$$f(S)\cup f(T)\subset f(S\cup T).$$

综上所述，有$f(S\cup T)=f(S)\cup f(T)$.

$(2)$对于任意的$x\in S\cap T$来说，有$x\in S$且$x\in T$.因为$S\cap T\subset S$，故

$$f(x)\in f(S\cap T) \subset f(S)$$

成立.同时，由于$S\cap T\subset T$，有$f(x)\in f(S\cap T) \subset f(T)$成立.

可知$f(x)\in f(S\cap T) \subset f(S)$且$f(x)\in f(S\cap T) \subset f(T)$.

于是$f(S\cap T) \subset f(S)\cap f(T)$.

但是$f(S\cap T) \subset f(S)\cap f(T)$中的包含关系一般来说不能换成相等关系.比如说，设函数$f=x-[x],x\in X=R$，取$S=[0,1) \subset X$，$T=[2,3)\subset X$，则$f(S)=f(T)=[0,1)$，于是$f(S)\cap f(T) =[0,1)$.但是因为$S\cap T=\varnothing $，$f(S\cup T)=f(\varnothing )=\varnothing $.最后$f(S)\cup f(T)\subsetneq f(S\cap T)$.

$4$.集合$S$的全体子集的集合记作

$$\mathcal{P}(S)=\lbrace T\mid T\subset S\rbrace .$$

例如$S=\lbrace s_1 ,s_2 ,\cdots ,s_n \rbrace $是$n$个元素的有限集，则$\mathcal{P}(S)$由空集$\varnothing$，$n$个单元集$\lbrace s_1 \rbrace $，$\lbrace s_2 \rbrace $，$\cdots $，$\lbrace s_n \rbrace $，$\dfrac{n(n-2)}{2}$个二元集$\lbrace s_i ,s_j \rbrace $，$1 \leq i < j \leq n$，等等，直到全集$T=S$组成.集合$\mathcal{P}(S)$的基数是多少？

解：由题意知，$\mathcal{P}(S)$的子集元素个数为$0$的个数为$C_n^0$，$\mathcal{P}(S)$的子集元素个数为$1$的个数为$C_n^1$，$\mathcal{P}(S)$的子集元素个数为$2$的个数为$C_n^2$，依此类推，$\mathcal{P}(S)$的子集元素个数为$n$的个数为$C_n^n$，所以一个$n$个元素的有限集共有：$C_n^0 +C_n^1 +\cdots +C_n^n$个子集.

根据二项式定理，有

$$C_n^0 +C_n^1 +\cdots +C_n^n =(1+1)^n =2^n.$$

故集合$\mathcal{P}(S)$的基数是$2^n$个.

$5$.设$f:X\to Y$是一个映射，且设对某个元素$a\in X$，$b=f(a)$.原像

$$f^{-1}(b)=f^{-1}(f(a))=\lbrace x\mid f(x)=f(a)\rbrace $$

叫作元素$b\in \text{Im}f$上的纤维.证明集合$X$是互不相交的纤维的并(也就是说，给出了$X$的一个划分).

注意：符号$f^{-1}(b)$不能联想到逆映射，后者可能并不存在.

证明：对每个元素$a\in X$，规定

$$f_a^{-1} =\lbrace x\in X\mid f(x)=f(a) \rbrace $$

这样得到$X$的一组子集$\lbrace f_a^{-1}\mid a\in X\rbrace $.证明它是$X$的一个划分.首先，由于反身性，$f(a)=f(a)$，所以$a\in f_a^{-1}$，于是

$$X=\underset{a\in X}{\bigcup}f_a^{-1} .$$

其次证明，若$f_a^{-1}\cap f_b^{-1}\neq \varnothing$，则$f(a)=f(b)$且$f_a^{-1} =f_b^{-1} $.设$f_a^{-1} \cap f_b^{-1} \neq \varnothing $，取一个$c\in f_a^{-1}\cap f_b^{-1} $，于是$f(c)=f(a)$，$f(c)=f(b)$，由对称性，$f(a)=f(c)$，再由传递性，得$f(a)=f(b)$.其次对任一元素$x\in f_a^{-1} $，有$f(x)=f(a)$，由传递性得$f(x)=f(b)$，从而$x\in f_b^{-1} $，所以$f_a^{-1}\subset f_b^{-1} $.再由对称性，$f(b)=f(a)$，同理得$f_b^{-1}\subset f_a^{-1} $.所以$f_a^{-1}=f_b^{-1}$.由此可知$\lbrace f_a^{-1} \mid a\in X\rbrace$，把重复的去掉之后，就是$X$的一个划分.也即集合$X$是互不相交的纤维的并.

$6$.证明有限个可数集的笛卡儿积也是可数集.

证明：欲证有限个可数集的笛卡儿积也是可数集，可设$\lbrace A_n \rbrace _{n\in J} $是有标集合，$J$是有限集，且对每个$n\in J$，$A_n $是可数集合，则$\displaystyle \prod_{n\in J} $是可数集合.

下面我们开始证明.不妨设$J=\lbrace 1,2,\cdots ,n\rbrace $，并假定对$n\in J$，$A_n \neq \varnothing $，则$\displaystyle \prod_{n\in J} A_n =A_1 \times A_2 \times \cdots \times A_n $.我们用数学归纳法证明$A_1 \times A_2 \times \cdots \times A_n $是可数集合.

当$n=2$时，由于$A_1 ,A_2 $是可数集合，则存在满射$f_i :Z_{+} \to A_i $，$(i=1,2)$，我们定义$h:Z_{+} \times Z_{+} \to A_1 \times A_2 $为$h=((m,k)) =(f_1 (m) ,f_2 (k)) $，易证$h$是满射.又$Z_{+} \times Z_{+} $是可数集合，因而存在满射$\varphi :Z_{+} \to Z_{+} \times Z_{+} $，从而$h\circ \varphi :Z_{+} \to A_1 \times A_2 $，根据定理

设$X,Y$和$Z$都是集合，$f:X\to Y,g:Y\to Z$，如果$f$和$g$都是满射，则$g\circ f:X\to Z$是满射；如果$f$和$g$都是单射，则$g\circ f:X\to Z$也是单射.因此，如果$f$和$g$都是一一映射，则$g\circ f:X\to Z$也是一一映射.

知$h\circ \varphi $是满射，从而由定理

设$B$是一个非空集合，则下列条件是等价的：$(1)\,B$是一个可数集；$(2)$存在满射$f:Z_{+} \to B$.$(3)$存在单射$g:B\to Z_{+} $.

证明：$(1)\Rightarrow (2)$.设$B$是可数集合，若是可数无限集，由定义[如果存在一个从集合$X$到正整数集$Z_{+} $的双射，则称集合$X$是一个可数无限集.]必存在双射$f:Z_{+} \to B$，而双射$f$就是满射.如果$B$是可数有限集，又$B\neq \varnothing $，由定义[设$X$是一个集合，如果$X$是空集或者存在正整数$n\in Z_{+} $使得集合$X$和集合$\lbrace 1,2,\cdots ,n\rbrace $之间有一个一一映射，则称集合$X$是一个有限集.]必存在整数$n$及双射$h:\lbrace 1,2,\cdots ,n\rbrace \to B$.我们定义$h$的扩张$f:Z_{+} \to B$如下：

$$f(i)=\begin{cases} h(i), & i\leq n \\ h(1), & i > n \end{cases}$$

显然，扩张$f:Z_{+} \to B$是满射.

$(2)\Rightarrow (3)$设$f:Z_{+} \to B$是满射，我们定义$g:B\to Z_{+} $为$g(b) =\min{f^{-1}(\lbrace b\rbrace )}$，由于$f$是满射，因此$f^{-1}(\lbrace b\rbrace ) \neq \varnothing $，因此，$f^{-1}(\lbrace b\rbrace ) $作为$Z_{+} $的子集其最小元必存在，因此$g$的定义是合理的.下证$g$是单射.

设$b,b’\in B$，$b\neq b’$则必有$f^{-1}(\lbrace b\rbrace ) \cap f^{-1}(\lbrace b’\rbrace ) =\varnothing $，因此$\min{f^{-1}(\lbrace b\rbrace )} \neq \min{f^{-1}(\lbrace b’\rbrace )} $，因此$g(b)\neq g(b’)$.

$(3)\Rightarrow (1)$设$g:B\to Z_{+} $是一个单射，这样我们就得到一个双射$g’:B\to g(B)$，对$b\in B$，$g’(b)=g(b) $.显然$g(B)\subseteq Z_{+} $.

如果$g(B)$是有限集，由于$g’:B\to g(B)$为双射，则$B$也是有限集，从而$B$是可数集合.

如果$g(B)$是无限集，由于$g(B)\subseteq Z_{+} $，由定理[如果$C$是$Z_{+} $的一个无限子集，那么$C$是可数无限集.]可知$g(B)$是可数无限集，由于$g’:B\to g(B)$是双射，从而$B$也是可数无限集，因而$B$是可数集合.

知$A_1 \times A_2 $是可数集合.

假设$A_1 \times A_2 \times \cdots \times A_{k-1} $是可数集合，由$n=2$时的结论可知$(A_1 \times A_2 \times \cdots \times A_{k-1} )\times A_k $是可数集合，因而存在满射$\varphi :Z_{+} \to (A_1 \times A_2 \times \cdots \times A_{k-1} )\times A_k $，我们再构造映射

$$f:(A_1 \times A_2 \times \cdots \times A_{k-1} )\times A_k \to A_1 \times A_2 \times \cdots \times A_{k-1} \times A_k .$$

定义

$$f(((a_1 ,a_2 ,\cdots ,a_{k-1}),a_k)) =(a_1 ,a_2 ,\cdots ,a_{k-1} ,a_k) ,$$

显然$f$是一一映射的，因此$f\circ \varphi :Z_{+} \to A_1 \times A_2 \times \cdots \times A_k $是满射，因此由知$A_1 \times A_2 \times \cdots \times A_k $是可数集合.

从而由归纳原理可知，$A_1 \times A_2 \times \cdots \times A_n $是可数集合.

$7$.符号$S\vartriangle T$表示两个集合$S$与$T$的对称差：$S\vartriangle T=(S\backslash T)\cup (T\backslash S)$(见图$6$).证明$S\vartriangle T=(S\cup T)\backslash (S\cap T)$.

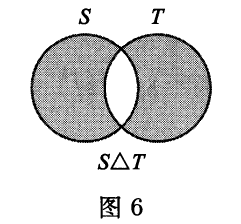
证明：由题意及图示可知，$S\cup T$由三部分构成：

$$S\cup T =(S\backslash T)\cup (S\cap T)\cup (T\backslash S).$$

这时，

$$(S\cup T)\backslash (S\cap T) =((S\backslash T)\cup (S\cap T)\cup (T\backslash S))\backslash (S\cap T) =(S\backslash T)\cup (T\backslash S).$$

根据题意所定义的对称差：$S\vartriangle T=(S \backslash T)\cup (T\backslash S)$，知

$$S\vartriangle T =(S\cup T)\backslash (S\cap T) .$$