华南理工大学2009年攻读硕士学位研究生入学考试试卷
科目名称:数学分析
适用专业:基础数学,计算数学,概率论与数理统计,应用数学,运筹学与控制论
$1$.($10$分)设函数$f(x)=\varphi (a+bx)-\varphi (a-bx)$,其中$\varphi (x)$在$x=a$的某个小邻域内有定义且在该点处可导,求$f’(0)$.
解:由导数定义,以及$\varphi (x)$在$x=a$的某个小邻域内有定义且在该点处可导,可知
$$\begin{align}
& f’(0) \\
= & \lim_{x\to 0} \dfrac{f(x)-f(0)}{x-0} \\
= & \lim_{x\to 0} \dfrac{(\varphi (a+bx)-\varphi (a-bx))-(\varphi (a)-\varphi (a))}{x} \\
= & \lim_{x\to 0} \dfrac{(\varphi (a+bx)-\varphi (a))-(\varphi (a-bx)-\varphi (a))}{x} \\
= & \lim_{x\to 0} \dfrac{\varphi (a+bx)-\varphi (a)}{x}-\lim_{x\to 0} \dfrac{\varphi (a-bx)-\varphi (a)}{x} \\
= & \lim_{x\to 0} b\cdot \dfrac{\varphi (a+bx)-\varphi (a)}{a+bx-a} -\lim_{x\to 0} (-b)\cdot \dfrac{\varphi (a-bx)-\varphi (a)}{a-bx-a} \\
= & b\varphi’ (a)-(-b)\varphi’ (a)\\
= & 2b\varphi’ (a)
\end{align}$$
即$f’(0)=2b\varphi’ (a)$.
$2$.($10$分)设$0 < x < y < \pi$,证明
$$y\sin{y} +2\cos{y} +\pi y > x\sin{x} +2\cos{x} +\pi x.$$
证明:令函数$f(x)=x\sin{x} +2\cos{x} +\pi x$,其中$0 < x < \pi $.
对函数$f(x)$求一阶导,有
$$\begin{align}
& f’(x) \\
= & (x\sin{x} +2\cos{x} +\pi x)’\\
= & \sin{x} +x\cos{x} -2\sin{x} +\pi \\
= & x\cos{x} -\sin{x} +\pi
\end{align}$$
对函数$f’(x)$再求导,有
$$\begin{align}
& f’’(x) \\
= & (x\cos{x} -\sin{x} +\pi )’\\
= & \cos{x} -x\sin{x} -\cos{x} \\
= & -x\sin{x}
\end{align}$$
因此,当$0 < x < \pi$时,可知$f’’(x) < 0$,于是可知$f’(x)$在区间$x\in (0,\pi )$上是严格单调递减的.
这时有
$$f’(x) > f’(\pi ) =0.$$
因此可知函数$f(x)$在区间$x\in (0,\pi )$上是严格单调递增的,那么对于任意的$x,y$,其中$0 < x < y < \pi $就有
$$f(y) > f(x)$$
即
$$y\sin{y} +2\cos{y} +\pi y > x\sin{x} +2\cos{x} +\pi x.$$
$3$.($10$分)设$x > 0,y > 0$,求$f(x,y)=x^2y(4-x-y)$的极值.
解:由于
$$\begin{align}
& f(x,y) \\
= & x^2y(4-x-y)\\
= & 4x^2y-x^3y-x^2y^2
\end{align}$$
对其求偏导数得:
$$\begin{align}
& f_x (x,y)=8xy-3x^2y-2xy^2=xy(8-3x-2y),\\
& f_y (x,y)=4x^2-x^3-2xy^2=x^2(4-x-2y),\\
& f_{xx} (x,y)=8y-6xy-2y^2,\\
& f_{yy} (x,y)=-2x^2,\\
& f_{xy} (x,y)=f_{yx} (x,y)=8x-3x^2-4xy.
\end{align}$$
注意到$x > 0,y > 0$,由方程组
$$\begin{cases} f_x (x,y)=8xy-3x^2y-2xy^2=xy(8-3x-2y)=0, \\ f_y (x,y)=4x^2-x^3-2xy^2=x^2(4-x-2y)=0\end{cases},$$
可得稳定点$P_0 (2,1)$为唯一的极值点.
又因为
$$f_{xx } (P_0 )=8\cdot 1-6\cdot 2\cdot 1-2\cdot 1^2 =-6 < 0,$$
$$(f_{xx } f_{yy } -f_{xy }^2)(P_0 )=(-6)\cdot (-2\cdot 2^2)-(8\cdot 2 -3\cdot 2^2-4\cdot 2\cdot 1)^2=32 > 0,$$
根据判别规则,知点$P_0 (2,1)$是极大值点.
此时极大值为$f(2,1)=2^2 \cdot 1\cdot (4-2-1)=4$.
$4$.($10$分)设$f(x)=\dfrac{\displaystyle \int_0^x du \int_0^{u^2} \arctan{(1+t)} dt}{x(1-\cos{x} )} $,求$\displaystyle \lim_{x\to 0} f(x) $.
解:令$\displaystyle g(u)=\int_0^{u^2} \arctan{(1+t)} dt$,对函数$g(u)$求导有
$$g’(u)=2u\cdot \arctan{(1+u^2)} .$$
于是,
$$\begin{align}
\lim_{x\to 0} f(x) & =\lim_{x\to 0} \dfrac{\displaystyle \int_0^x g(u) du }{x(1-\cos{x} )} \\
& =\lim_{x\to 0} \dfrac{\displaystyle \int_0^x g(u) du }{x\cdot \dfrac{x^2}{2} } (\because 1-\cos{x} \sim \dfrac{x^2}{2} (x\to 0))\\
& =\lim_{x\to 0} \dfrac{g(x)}{\dfrac{3x^2}{2} } \\
& =\lim_{x\to 0} \dfrac{g’(x)}{3x} \\
& =\lim_{x\to 0} \dfrac{2x\cdot \arctan{(1+x^2)} }{3x} \\
& =\dfrac{2}{3} \cdot \arctan{1} \\
& =\dfrac{2}{3} \times \dfrac{\pi }{4} \\
& =\dfrac{\pi }{6} \\
\end{align}$$
即
$$\lim_{x\to 0} f(x) =\dfrac{\pi }{6} .$$
$5$.($10$分)计算$\displaystyle \oint_c xdy -ydx$,其中$c$为椭圆$(x+2y)^2+(3x+2y)^2=1$,方向为逆时针方向.
解:作变换:
$$\begin{cases} x+2y=s \\ 3x+2y=t\end{cases} ,$$
则有
$$\begin{cases} x=\dfrac{-s+t}{2} \\ y=\dfrac{3s-t}{4} \end{cases} ,$$
其中$L:s^2+t^2=1$.
于是
$$\oint_c xdy -ydx=\oint_L \dfrac{-s+t}{2} d\dfrac{3s-t}{4} -\dfrac{3s-t}{4} d\dfrac{-s+t}{2} =\dfrac{1}{4} \oint_L (tds -sdt ).$$
接着,对曲线$L$作变换:
$$\begin{cases} s=\cos{u} \\ t=\sin{u} \end{cases} (0\leq u \leq 2\pi ),$$
代入计算得:
$$\oint_c xdy -ydx=\dfrac{1}{4} \oint_L (tds -sdt )=\dfrac{1}{4} \int_0^{2\pi } (\sin{u} d\cos{u} -\cos{u} d\sin{u} )=\dfrac{1}{4}(-2\pi )=-\dfrac{\pi }{2} .$$
$6$.($10$分)计算
$$\underset{S}{\iint } (x-y)\,dx\,dy+x(y-z)\,dy\,dz ,$$
其中$S$为柱面$x^2+y^2=1$及平面$z=0,z=3$所围成的空间区域$\Omega $的整个边界曲面外侧.
解:由高斯公式得:
$$\begin{align}
& \underset{S}{\iint } (x-y)\,dx\,dy+x(y-z)\,dy\,dz \\
= & \underset{S}{\iint } x(y-z)\,dy\,dz+0\,dz\,dx+(x-y)\,dx\,dy\\
= & \underset{V}{\iiint } \dfrac{\partial x(y-z)}{\partial x} +\dfrac{\partial 0}{\partial 0} +\dfrac{\partial (x-y)}{\partial z} \,dx\,dy\,dz\\
= & \underset{V}{\iiint } (y-z)\,dx\,dy\,dz\\
\end{align}$$
下设$D:x^2+y^2 \leq 1$,则$V=\lbrace (x,y,z)\mid (x,y)\in D,0 \leq z \leq 3\rbrace $,采用极坐标变换
$$T:\begin{cases} x=r\cos{\theta } \\ y=r\sin{\theta } \end{cases} ,0\leq r \leq 1,0\leq \theta \leq 2\pi .$$
于是就有
$$\begin{align}
& \underset{S}{\iint } (x-y)\,dx\,dy+x(y-z)\,dy\,dz \\
= & \underset{V}{\iiint } (y-z)\,dx\,dy\,dz\\
= & \underset{D}{\iint } \,dx\,dy\int_0^3 (y-z)\,dz\\
= & \underset{D}{\iint } \left( 3y-\dfrac{9}{2} \right) \,dx\,dy\\
= & \int_0^{2\pi} \,d{\theta } \int_0^1 \left( 3r\sin{\theta } -\dfrac{9}{2} \right) r\,dr (\because 极坐标变换 T)\\
= & -\dfrac{9}{2} \pi \\
\end{align}$$
$7$.($15$分)设$f(x)=\sin{\sqrt{x} } $,判断$f(x)$在$[0,+\infty )$上是否一致连续,并给出证明.
答:函数$f(x)$在$[0,+\infty )$上一致连续.
证明如下:
先证明函数$f(x)=\sin{\sqrt{x} } $在$[1,+\infty )$上一致连续.
$\forall \varepsilon > 0$,取$\delta < \min{\lbrace 2\varepsilon ,\dfrac{\pi }{2} \rbrace }$,则当$x_1 ,x_2 \in [1,+\infty )$,且$\mid x_1 -x_2 \mid < \delta $时,
$$\begin{align}
& \mid f(x_1 ) -f(x_2 ) \mid \\
= & \mid \sin{\sqrt{x_1 } } -\sin{\sqrt{x_2 } } \mid \\
= & \mid 2\cos{\left( \dfrac{\sqrt{x_1 } +\sqrt{x_2 } }{2} \right) } \sin{\left( \dfrac{\sqrt{x_1 } -\sqrt{x_2 } }{2} \right) } \mid \\
\leq & 2\mid \sin{\left( \dfrac{\sqrt{x_1 } -\sqrt{x_2 } }{2} \right) } \mid \\
\leq & \mid \sqrt{x_1 } -\sqrt{x_2 } \mid \\
= & \dfrac{\mid x_1 -x_2 \mid }{\sqrt{x_1 } +\sqrt{x_2 } } \\
\leq & \dfrac{1}{2} \mid x_1 -x_2 \mid \\
< & \varepsilon .\\
\end{align}$$
所以$f(x)=\sin{\sqrt{x} } $在$[1,+\infty )$内一致连续.
补充规定$f(0)=0$,则$f(x)=\sin{\sqrt{x} } $在$[0,1]$上连续,从而一致连续.
由综上可知函数$f(x)=\sin{\sqrt{x} } $在$[0,+\infty )$上一致连续.
$8$.($15$分)计算积分$I=\displaystyle \underset{D}{\iint } \min{\lbrace x^2y ,2\rbrace } \,dx\,dy$,其中
$$D=\lbrace (x,y)\mid 0\leq x\leq 4,0\leq y\leq 3\rbrace .$$
解:
1 | a = Solve[y == 2/{x*x} && y == 3, {x, y}]; |
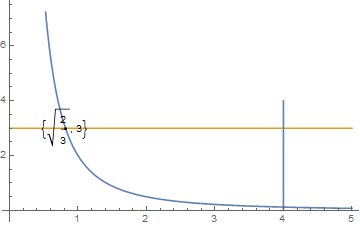
如上图所示,函数$x^2y=2$把积分区域$D=\lbrace (x,y)\mid 0\leq x\leq 4,0\leq y\leq 3\rbrace $划分成两部分.
可把积分区域$D=\lbrace (x,y)\mid 0\leq x\leq 4,0\leq y\leq 3\rbrace $分割成三部分,分别为
$$D_1 =\lbrace (x,y)\mid 0\leq x\leq \sqrt{\dfrac{2}{3} } ,0\leq y\leq 3\rbrace ,$$
$$D_2 =\lbrace (x,y)\mid \sqrt{\dfrac{2}{3} } \leq x\leq 4,0\leq y\leq \dfrac{2}{x^2} \rbrace ,$$
$$D_3 =\lbrace (x,y)\mid \sqrt{\dfrac{2}{3} } \leq x\leq 4,\dfrac{2}{x^2} \leq y\leq 3\rbrace .$$
因此,
$$\begin{align}
I & =\underset{D}{\iint } \min{\lbrace x^2y ,2\rbrace } \,dx\,dy \\
& =\underset{D_1 }{\iint } \min{\lbrace x^2y ,2\rbrace } \,dx\,dy +\underset{D_2 }{\iint } \min{\lbrace x^2y ,2\rbrace } \,dx\,dy +\underset{D_3 }{\iint } \min{\lbrace x^2y ,2\rbrace } \,dx\,dy\\
& =\underset{D_1 }{\iint } x^2y\,dx\,dy +\underset{D_2 }{\iint } x^2y\,dx\,dy +\underset{D_3 }{\iint } 2\,dx\,dy \\
& =\int_0^{\sqrt{\frac{2}{3} } } \,dx \int_0^3 x^2y\,dy +\int_{\sqrt{\frac{2}{3} } }^{4}\,dx \int_0^{\frac{2}{x^2} } x^2y\,dy +\int_{\sqrt{\frac{2}{3} } }^{4}\,dx \int_{\frac{2}{x^2} }^3 x^2y\,dy\\
& =\int_0^{\sqrt{\frac{2}{3} } } \dfrac{9}{2} x^2\,dx +\int_{\sqrt{\frac{2}{3} } }^{4} \dfrac{2}{x^2} \,dx +\int_{\sqrt{\frac{2}{3} } }^{4} \left( 6-\dfrac{4}{x^2} \right) \,dx \\
& =\dfrac{3}{2} x^3{\Large \mid } _0^{\sqrt{\frac{2}{3} } } -\dfrac{2}{x} {\Large \mid} _{\sqrt{\frac{2}{3} } }^{4} +( 6x+\dfrac{4}{x} ) {\Large \mid} _{\sqrt{\frac{2}{3} } }^4 \\
& =\sqrt{\dfrac{2}{3} } -\dfrac{1}{2} +\sqrt{6} +25-4\sqrt{6} \\
& =\dfrac{49}{2} -\dfrac{8}{3} \sqrt{6} .\\
\end{align}$$
$9$.($15$分)计算积分$I(y)=\displaystyle \int_0^{+\infty } e^{-x^2}\sin{2xy} \,dx$.
解:$(1)$ 先证明
$$\displaystyle \int_0^{+\infty } e^{-x^2}\,dx=\dfrac{\sqrt{\pi } }{2} .$$
首先,考察$S_a =[0,a]\times [0,a]$上的积分
$$\underset{S_a}{\iint } e^{-(x^2+y^2)}\,d\sigma .$$
因为
$$\underset{S_a}{\iint } e^{-(x^2+y^2)}\,d\sigma =\int_0^a e^{-x^2}\,dx \int_0^a e^{-y^2}\,dy =\left( \int_0^a e^{-x^2}\,dx \right) ^2 .$$
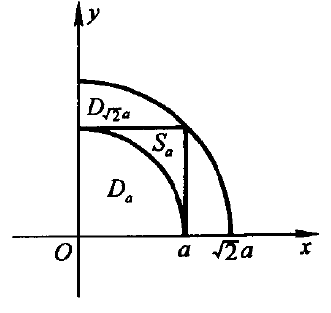
由$D_a \subset S_a \subset D_{\sqrt{2}a } $(上图)知
$$\begin{align}
\underset{D_a }{\iint } e^{-(x^2+y^2)}\,d\sigma & \leq \underset{S_a }{\iint } e^{-(x^2+y^2)}\,d\sigma \\
& =\left( \int_0^a e^{-x^2}\,dx \right) ^2 \leq \underset{D_{\sqrt{2} a } }{\iint } e^{-(x^2+y^2)}\,d\sigma .\\
\end{align}$$
令$a\to +\infty $,则得
$$\lim_{a\to +\infty } \left( \int_0^a e^{-x^2}\,dx \right) ^2 =\underset{D}{\iint } e^{-(x^2+y^2)}\,d\sigma =\dfrac{\pi }{4} .$$
所以
$$\displaystyle \int_0^{+\infty } e^{-x^2}\,dx=\dfrac{\sqrt{\pi } }{2} .$$
$(2)$由于$\mid e^{-x^2}\sin{2xy} \mid \leq e^{-x^2}$对任一实数$y$成立及反常积分$\displaystyle \int_0^{+\infty } e^{-x^2}\,dx \left( =\dfrac{\sqrt{\pi } }{2} \right) $收敛,所以积分$I(y)=\displaystyle \int_0^{+\infty } e^{-x^2}\sin{2xy} \,dx$在$y\in (-\infty ,+\infty )$上收敛.
考察含参量反常积分
$$\displaystyle \int_0^{+\infty } (e^{-x^2}\sin{2xy} )’_r \,dx=\int_0^{+\infty } 2xe^{-x^2}\cos{2xy} \,dx .$$
由于$\mid 2xe^{-x^2}\cos{2xy} \mid \leq $对一切$x\geq 0,-\infty < y < +\infty $成立,且反常积分
$$\begin{align}
\int_0^{+\infty } 2xe^{-x^2}\,dx & =\lim_{u\to +\infty } \int_0^u 2xe^{-x^2}\,dx \\
& = -\lim_{u\to +\infty } \int_0^u e^{-x^2}\,d(-x^2) \\
& = -\lim_{u\to +\infty } e^{-x^2} {\Large \mid }_0^u \\
& = -\lim_{u\to +\infty } (e^{-u^2} -e^{-0^2}) \\
& = -(0-1) \\
& = 1 \\
\end{align}$$
收敛,根据魏尔斯特拉斯$M$判别法,含参量积分$\displaystyle \int_0^{+\infty } (e^{-x^2}\sin{2xy} )’_r \,dx=\int_0^{+\infty } 2xe^{-x^2}\cos{2xy} \,dx $在$y\in (-\infty ,+\infty )$上一致收敛.
综合上述结果由含参量反常积分的可微性,即得
$$\begin{align}
I’(y) & =\int_0^{+\infty } 2xe^{-x^2}\cos{2xy} \,dx \\
& = \lim_{A\to +\infty } \int_0^A 2xe^{-x^2}\cos{2xy} \,dx \\
& = \lim_{A\to +\infty } \left( -e^{-x^2}\cos{2xy} {\Large \mid}_0^A -\int_0^A 2ye^{-x^2}\sin{2xy} \,dx \right) \\
& = 1-\int_0^{+\infty } 2ye^{-x^2}\sin{2xy} \,dx \\
& = 1-2yI(y).\\
\end{align}$$
即
$$I’(y)+2yI(y)=1.$$
对上式左乘和右乘$e^{y^2}$,有$e^{y^2}I’(y)+2ye^{y^2}I(y)=e^{y^2}$.
即有
$$(e^{y^2}I(y))’=e^{y^2}.$$
那么有
$$\int_0^y e^{t^2}I(t)\,dt =\int_0^y e^{t^2}\,dt+I(0).$$
对上式可解出
$$\begin{align}
I(y) & =e^{-y^2}\left( \int_0^y e^{t^2}\,dt+I(0) \right) \\
& =e^{-y^2} \int_0^y e^{t^2}\,dt .\\
\end{align}$$
$10$.($15$分)设$f(x,y)=\begin{cases} \dfrac{xy^2}{x^2+y^2} , & 当x^2+y^2\neq 0,\\ 0, & 当x^2+y^2= 0.\end{cases} $讨论以下性质
$i)f(x,y)$的连续性,
$ii)f_x ,f_y $的存在性及连续性,
$iii)f(x,y)$的可微性.
解:
$i)$当$x^2+y^2\neq 0$时,显然函数$f(x,y)$在点$(x,y)$处是连续的;
当$x^2+y^2= 0$时,因为
$$\mid \dfrac{xy^2}{x^2+y^2} -0\mid =\mid \dfrac{xy^2}{x^2+y^2} \mid =\mid \dfrac{y^2}{x^2+y^2} \cdot x\mid \leq \mid x\mid .$$
故对$\forall \varepsilon > 0,\exists \delta =\varepsilon > 0$,当$\mid x \mid < \delta , \mid y \mid < \delta $时,有
$$\mid f(x,y)-f(0,0)\mid =\mid \dfrac{xy^2}{x^2+y^2} \mid \leq \mid x\mid < \varepsilon $$
故$f(x,y)$在原点处连续.
$ii)$当$x^2+y^2\neq 0$时,函数$f(x,y)$在任意点$x$的某一邻域内有定义,根据偏导数的定义,极限
$$\begin{align}
& \lim_{\Delta x\to 0} \dfrac{\Delta _x f(x,y)}{\Delta x} \\
= & \lim_{\Delta x\to 0} \dfrac{f(x+\Delta x ,y)-f(x,y)}{\Delta x} \\
= & \lim_{\Delta x\to 0} \dfrac{\dfrac{(x+\Delta x)y^2}{(x+\Delta x)^2+y^2}-\dfrac{xy^2}{x^2+y^2} }{\Delta x} \\
= & \lim_{\Delta x\to 0} \dfrac{(x+\Delta x)y^2(x^2+y^2)-xy^2[(x+\Delta x)^2+y^2]}{\Delta x[(x+\Delta x)^2+y^2] (x^2+y^2)} \\
= & \lim_{\Delta x\to 0} \dfrac{y^2(y^2\Delta x-x^2\Delta x-x{\Delta x}^2)}{\Delta x[(x+\Delta x)^2+y^2] (x^2+y^2)} \\
= & \lim_{\Delta x\to 0} \dfrac{y^2(y^2-x^2-x\Delta x])}{[(x+\Delta x)^2+y^2] (x^2+y^2)} \\
= & \dfrac{y^2(y^2-x^2)}{(x^2+y^2)^2} ,\\
\end{align}$$
存在.同理,函数$f(x,y)$在任意点$y$的某一邻域内有定义,根据偏导数的定义,极限
$$\begin{align}
& \lim_{\Delta y\to 0} \dfrac{\Delta _y f(x,y)}{\Delta y} \\
= & \lim_{\Delta y\to 0} \dfrac{f(x,y+\Delta y )-f(x,y)}{\Delta y} \\
= & \lim_{\Delta y\to 0} \dfrac{\dfrac{x(y+\Delta y)^2}{x^2+(y+\Delta y)^2} -\dfrac{xy^2}{x^2+y^2} }{\Delta y} \\
= & \lim_{\Delta y\to 0} \dfrac{x(y+\Delta y)^2(x^2+y^2)-xy^2[x^2+(y+\Delta y)^2]}{\Delta y[x^2+(y+\Delta y)^2] (x^2+y^2)} \\
= & \lim_{\Delta y\to 0} \dfrac{x(2x^2y\Delta y+x^2{\Delta y}^2)}{\Delta y[x^2+(y+\Delta y)^2] (x^2+y^2)} \\
= & \lim_{\Delta y\to 0} \dfrac{x(2x^2y+x^2\Delta y)}{[x^2+(y+\Delta y)^2] (x^2+y^2)} \\
= & \dfrac{2x^3y}{(x^2+y^2)^2} .\\
\end{align}$$
也存在.
可知当$x^2+y^2\neq 0$时,函数$f(x,y)$在任意点$(x,y)$存在关于$x,y$的偏导数$f_x ,f_y $.
同时,当$x^2+y^2\neq 0$时,显然函数$f(x,y)$在任意点$(x,y)$存在关于$x,y$的偏导数$f_x ,f_y $都是连续的.
当$x^2+y^2= 0$时,按偏导数定义
$$f_x (0,0)=\lim_{\Delta x\to 0} \dfrac{f(\Delta x,0)-f(0,0)}{\Delta x} =\lim_{\Delta x\to 0} \dfrac{0-0}{\Delta x} =0.$$
同理,可得
$$f_y (0,0)=\lim_{\Delta y\to 0} \dfrac{f(0,\Delta y)-f(0,0)}{\Delta y} =\lim_{\Delta y\to 0} \dfrac{0-0}{\Delta y} =0.$$
故可知当$x^2+y^2= 0$时,函数$f(x,y)$在原点$(0,0)$处存在关于$x,y$的偏导数$f_x ,f_y $.
但是,设动点$(x,y)$沿直线$y=kx$趋于$(0,0)$,由
$$\underset{y=kx}{\lim_{(x,y)\to (0,0)} } f_x (x,y)=\lim_{x\to 0} \dfrac{k^2x^2(k^2x^2-x^2)}{(x^2+k^2x^2)^2} =\lim_{x\to 0} \dfrac{k^2x^4(k^2-1)}{x^4(1+k^2)^2} =\dfrac{k^2(k^2-1)}{(1+k^2)^2} $$
与$k$有关.
故$\displaystyle \lim_{(x,y) \to (0,0)} f_x (x,y)$不存在,从而$f_x (x,y)$在$(0,0)$处不连续.
同理,设动点$(x,y)$沿直线$y=kx$趋于$(0,0)$,由
$$\underset{y=kx}{\lim_{(x,y)\to (0,0)} } f_y (x,y)=\lim_{x\to 0} \dfrac{2x^4k^2}{(x^2+k^2x^2)^2} =\lim_{x\to 0} \dfrac{2x^4k^2}{x^4(1+k^2)^2} =\dfrac{2k^2}{(1+k^2)^2} $$
与$k$有关.
故$\displaystyle \lim_{(x,y)\to (0,0)} f_y (x,y)$不存在,从而$f_y (x,y)$在$(0,0)$处不连续.
综上可知,$f(x,y)$处处对$x,y$可导,即$f_x ,f_y $处处存在.当$x^2+y^2\neq 0$时,函数$f(x,y)$在任意点$(x,y)$存在关于$x,y$的偏导数$f_x ,f_y $都是连续的.而当$x^2+y^2= 0$时,函数$f(x,y)$在原点$(0,0)$处存在关于$x,y$的偏导数$f_x ,f_y $却都是不连续的.
$iii)$当$x^2+y^2\neq 0$时,由$ii)$的结论,根据可微的充分条件定理,因为函数$f(x,y)$的偏导数$f_x ,f_y $处处存在,且偏导数$f_x ,f_y $处处连续,故函数$f(x,y)$在$x^2+y^2\neq 0$可微.
而当$x^2+y^2=0$时,在原点$(0,0)$处函数$f(x,y)$的全增量为:
$$\Delta f(0,0) =f(\Delta x,\Delta y) -f(0,0) =\dfrac{\Delta x\cdot \Delta y^2 }{\Delta x^2 +\Delta y^2 } -0=\dfrac{\Delta x\cdot \Delta y^2 }{\Delta x^2 +\Delta y^2 } .$$
由于
$$\lim_{\rho \to 0} \dfrac{\mid \Delta f(0,0)-f_x (0,0)\Delta x-f_y (0,0)\Delta y\mid }{\rho } =\lim_{\rho \to 0} \dfrac{\dfrac{\Delta x\cdot \Delta y^2 }{\Delta x^2 +\Delta y^2 } }{\rho } =\underset{\Delta y\to 0}{\lim_{\Delta x\to 0} } \dfrac{\Delta x\cdot \Delta y^2 }{(\Delta x^2 +\Delta y^2 )^{\frac{3}{2} } } \neq 0,$$
其中$\rho =\sqrt{\Delta x^2 +\Delta y^2 } $.
因此$f(x,y)$在点$(0,0)$处不可微.
$11$.($15$分)设$x_0 =\sqrt{6} ,x_{n+1 } =\sqrt{6+x_n } ,n=0,1,2,\cdots $,判断级数$\displaystyle \sum_{n=0 }^{\infty } \sqrt{3-x_n } $的敛散性.
解:级数$\displaystyle \sum_{n=0 }^{\infty } \sqrt{3-x_n } $收敛.
$(1)$首先,记$x_n =\sqrt{6+\sqrt{6+\cdots +\sqrt{6} } } $,易见数列$x_n $是递增的.现用数学归纳法来证明$\lbrace x_n \rbrace $有上界.
显然$x_1 =\sqrt{6} < 3$.假设$x_n < 3$,则有$x_{n+1 } =\sqrt{6+x_n } < \sqrt{6+3} =3$,从而对一切$n$有$x_n < 3$,即$\lbrace x_n \rbrace $有上界.
由单调有界定理,数列$\lbrace x_n \rbrace $有极限,记为$a$.由于
$$x_{n+1 }^2 =6+x_n ,$$
对上式两边取极限得$a^2=6+a$,即有
$$(a-3)(a+2)=0,$$
解得$a=3$或$a=-2$.
由数列极限的保不等式性,$a=-2$是不可能的,故有
$$\lim_{n \to \infty } \sqrt{6+\sqrt{6+\cdots +\sqrt{6} } } =3.$$
$(2)$由$(1)$,有
$$3-x_n =3-\sqrt{6+x_{n-1 } } =\dfrac{3-x_{n-1 } }{3+\sqrt{6+x_{n-1 } } } < \dfrac{1}{3} (3-x_{n-1 } ) < \cdots < \left( \dfrac{1}{3} \right) ^n (3-x_0 ) ,$$
于是有
$$\sqrt{3-x_n } < \dfrac{1}{\sqrt{3^n} } \sqrt{3-\sqrt{6} } .$$
因为级数$\displaystyle \sum_{n=0 }^{\infty } \dfrac{1}{\sqrt{3^n} } \sqrt{3-\sqrt{6} } $是收敛的,所以根据比较原则,知级数$\displaystyle \sum_{n=0 }^{\infty } \sqrt{3-x_n } $也是收敛的.
$12$.($15$分)设$f(x)$在$(-\infty ,+\infty )$内有连续的一阶导数,证明
$i)$若$\displaystyle \lim_{\mid x\mid \to +\infty } f’(x) =\alpha > 0$,则方程$f(x)=0$在$(-\infty ,+\infty )$内至少有一个实根.
$ii)$若$\displaystyle \lim_{\mid x\mid \to +\infty } f(x) =0$,则方程$f’(x)=0$在$(-\infty ,+\infty )$内至少有一个实根.
证明:$i)$由于$\displaystyle \lim_{\mid x\mid \to +\infty } f’(x) =\alpha > 0$,故对$\varepsilon =\dfrac{\alpha }{2} > 0$,存在$N_1 > 0$,当$\mid x \mid > N_1 $时,就有$\mid f’(x)-\alpha \mid < \varepsilon =\dfrac{\alpha }{2} $,即 $\dfrac{\alpha }{2} < f’(x) < \dfrac{3\alpha }{2} $.
因此,当$x > 0$充分大时,有
$$f(x)=f(N_1 )+\int_{N_1 }^x f’(s)\,ds \geq f(N_1 )+\dfrac{\alpha }{2} (x-N_1 ) > 0.$$
当$x < 0$充分小时,有
$$f(x)=f(-N_1 )-\int_x^{-N_1 } f’(s)\,ds \leq f(-N_1 )+\dfrac{\alpha }{2} (x+N_1 ) < 0.$$
由于$f(x)$在区间$(-\infty ,+\infty )$上连续,故根据根的存在定理得,方程$f(x)=0$在$(-\infty ,+\infty )$内至少有一个实根.
$ii)$如果$f(x)\equiv 0$,则结论显然成立.
如果$f(x)$不恒为零,则存在一点$a\in (-\infty ,+\infty )$,使得$f(a)\neq 0$,由于$\displaystyle \lim_{\mid x\mid \to +\infty } f(x) =0$,于是对$\varepsilon =\dfrac12 \mid f(a)\mid > 0$,存在$N_2 > 0$,当$\mid x \mid > N_2 $时,就有
$$\mid f(x)\mid < \varepsilon =\dfrac12 \mid f(a)\mid .$$
又函数$f(x)$在区间$[-N_2 -1,N_2 +1]$上连续,则必存在最大值或最小值,其最大值点或最小值点(可设为$x=\xi $)必然落在区间$[-N_2 -1,N_2 +1]$.
又因为当$\mid x\mid > N_2 $时,就有$\mid f(x)\mid < \varepsilon =\dfrac12 \mid f(a)\mid < \mid f(a)\mid $.故落在区间$[-N_2 -1,N_2 +1]$内的点$x=\xi $必是极值点,由于$f’(x)$在区间$[-N_2 -1,N_2 +1]$内存在,所以$f’(\xi )=0$.
因此,方程$f’(x)=0$在$(-\infty ,+\infty )$内至少有一个实根.

