习题

$1$.证明群$G$的任意子群族$\lbrace H_i \vert i\in I\rbrace $的交$\displaystyle \underset{i\in I}{\bigcap} H_i $是$G$的一个子群.

证明：设$H_1 ,H_2 ,\cdots $是群$G$的任意子群.

$1)\;$利用子群的定义，有$e\in H_1 ,e\in H_2 ,\cdots $，因此单位元$e\in \displaystyle \underset{i\in I}{\bigcap} H_i $.

$2)\;$对于任意的$x,y\in \displaystyle \underset{i\in I}{\bigcap} H_i $，则$x,y\in H_1 $，$x,y\in H_2 ,\cdots $.利用子群的定义，由$x,y\in H_1 $可知$xy\in H_1 $，$x,y\in H_2 $可知$xy\in H_2 ,\cdots $.因此，$xy\in \displaystyle \underset{i\in I}{\bigcap} H_i $.

$3)\;$对于任意的$x\in \displaystyle \underset{i\in I}{\bigcap} H_i $，有$x\in H_1 $，$x\in H_2 ,\cdots $.利用子群的定义，由$x\in H_1 $可知$x^{-1} \in H_1 $，$x\in H_2 $可知$x^{-1} \in H_2 ,\cdots $.因此，$x^{-1} \in \displaystyle \underset{i\in I}{\bigcap} H_i $.

利用子群的定义，结合上述三点，可证群$G$的任意子群族$\lbrace H_i \vert i\in I\rbrace $的交$\displaystyle \underset{i\in I}{\bigcap} H_i $是$G$的一个子群.

$2$.设$S$是群$G$的子集，称$G$是由$S$生成的，并记作$G=\langle S\rangle $，若包含$S$的所有子群的交与$G$重合.（换言之，在$G$中没有包含$S$的真子群.）证明，当$G=\langle S\rangle $时，任意元素$g\in G$形如$g=t_1 t_2 \cdots t_n $，$n=1,2,\cdots $，其中$t_i \in S$或$t_i^{-1} \in S$，$1\leq t\leq n$.

$3$.证明群$G$中乘法可换的元素$a,b$若有互素的阶$s,t$，则在$G$中生成一个$st$阶的循环子群：$\langle a,b\rangle =\langle ab\rangle $.

提示：包含$\langle ab\rangle \subset \langle a,b\rangle =\lbrace a^i b^j \vert 0\leq i\leq s-1,0\leq j\leq t-1\rbrace $显然成立.根据第$1$章$\S 9$第$3$段，从$(s,t)=1$可知，存在$k,l\in \mathbb{Z}$，使$tk+sl=1$.考虑到定理$1$，$a=a^{1-sl}=a^{tk}=a^{tk}b^{tk}=(ab)^{tk}\in \langle ab\rangle $.类似地，$b\in \langle ab\rangle $，故$\langle a,b\rangle \subset \langle ab\rangle $.

$4$.设$M=\langle S\rangle $是由集合$S$生成的幺半群，如果每个元素$s\in S$在$M$中可逆，证明$M$是一个群.

证明：由题意知，$M$是一个所有的元素都可逆的幺半群，故$M$是一个群.

$5$.证明下述论断：设$G$是一个幺半群，使得任取$a,b\in G$，方程$ax=b,ya=b$有唯一解，则$G$是一个群.

证明：取$b=e$，则$ax=e$有解$a_1 $，$ya=e$有解$a_2 $，这样有

$$a_1 =ea_1 =(a_2 a)a_1 =a_2 (aa_1 )=a_2 e=a_2 ,$$

故对任意$a\in G$，有$a_1 $满足$aa_1 =a_1 a=e$，故$G$是一个群.

$6$.令${\varphi }_{a,b} \colon x\mapsto ax+b(a,b\in \mathbb{R} ;a\neq 0)$是实直线上的一个仿射变换，它们的集合记作$A_1 (\mathbb{R} )$，在$A_1 (\mathbb{R} )$中定义乘法${\varphi }_{a,b} {\varphi }_{c,d} ={\varphi }_{ac,ad+b}$，证明$A_1 (\mathbb{R} )$是一个群.$A_1 (\mathbb{R} )$包含有一个子群$\mathrm{GL}_1 (\mathbb{R} )$，它使点$x=0$保持不动，也包含有一个由“纯位移”$x\mapsto x+b$组成的子群.

证明：任取${\varphi }_{a_i ,b_i } (x)=a_i x+b_i $，其中$a_0 \neq 0,i=1,2$.由于

$$({\varphi }_{a_1 ,b_1 } \circ {\varphi }_{a_2 ,b_2 } )(x)={\varphi }_{a_1 a_2 ,a_1 b_2 +b_1 } (x) =a_1 a_2 x+(a_1 b_2 +b_1 ),$$

因此${\varphi }_{a_1 ,b_1 } \circ {\varphi }_{a_2 ,b_2 } \in A_1 (\mathbb{R} )$.这说明映射的乘法是$A_1 (\mathbb{R} )$的一个运算.映射的乘法适合结合律.$\mathbb{R} $上的恒等映射$1_{\mathbb{R} } (x)=x$是一次函数，它是$A_1 (\mathbb{R} )$的单位元.一次函数${\varphi }_{a,b} (x)=ax+b$有反函数${\varphi }_{a,b}^{-1} (x)=\dfrac{1}{a} x-\dfrac{b}{a}$，${\varphi }_{a,b}^{-1} $仍是一次函数.综上所述，$A_1 (\mathbb{R} )$对于映射的乘法${\varphi }_{a,b} {\varphi }_{c,d} ={\varphi }_{ac,ad+b}$成为一个群.

$7$.群$\mathrm{SL}_2 (\mathbb{Z} )$包含有元素$A=\begin{pmatrix} 0 & 1 \\ -1 & 0 \end{pmatrix}$和$B=\begin{pmatrix} 0 & 1 \\ -1 & -1 \end{pmatrix}$，阶数分别为$4$和$3$.证明$\langle AB\rangle $是$\mathrm{SL}_2 (\mathbb{Z} )$中的无限循环子群.这说明群$G$中两个有限阶元素的乘积不一定是有限阶元.这件事在阿贝尔群中成立吗？

证明：$1)\;$由题意知$AB=\begin{pmatrix} -1 & -1 \\ 0 & -1 \end{pmatrix}$，易验证矩阵$\begin{pmatrix} -1 & -1 \\ 0 & -1 \end{pmatrix}$生成$\mathrm{SL}_2 (\mathbb{Z} )$的一个无限循环子群，故$\langle AB\rangle $是$\mathrm{SL}_2 (\mathbb{Z} )$中的无限循环子群.

$2)\;$这件事在阿贝尔群中不成立，因为此时两个有限阶元素的乘积一定是有限阶元.$a,b$是群$G$中的元素，$ab=ba,o(a)=m,o(b)=n,o(ab)=k$，则$o(ab)\vert [m,n],\dfrac{[m,n]}{(m,n)} \vert o(ab)$.特别地，当$(m,n)=1$时，$o(ab)=mn$.其中$[m,n]$表示正整数$m$与$n$的最小公倍数，$(m,n)$表示正整数$m$与$n$的最大公约数 ，由数论的知识有$[m,n] (m,n)=mn$.对于群中元素$a$，$o(a)$表示$a$的阶.证明如下：

首先，$(ab)^{[m,n]} =(a^m)^{\dfrac{[m,n]}{m} } (b^n)^{\dfrac{[m,n]}{n} } =1$，故$o(ab)\vert [m,n]$.其次，$(ab)^{o(ab)} =1$，则$1=(ab)^{o(ab)m} =(a^m)^{o(ab)}b^{o(ab)m} =b^{o(ab)m}$，故$n\vert o(ab)m$.于是$\dfrac{n}{(m,n)} \vert o(ab)$，同理$\dfrac{[m,n]}{(m.n)} =\dfrac{m}{(m,n)} \dfrac{n}{(m.n)} \vert o(ab)$.若$(m,n)=1$，由上即得$o(ab)=mn$.

记$d=(m,n)$，由上面的证明可设$k=\dfrac{mn}{d^2} l$，其中$1\leq l\leq d$且$l\vert d$.

参考文献：

[1]范兴亚.关于群中两可交换元素乘积的阶.首都师范大学学报：第27卷第4期,2006年8月

$8$.证明若群$G$的阶$\vert G\vert =2n$是偶数，则$G$中包含有一个二阶元$g\neq e$.

提示：观察$G$用元素对$g,g^{-1}$的划分.

证明：假如$G$中没有二阶元，则对于每一个非单位元$g$都有$g\neq g^{-1}$.从而$G$中的所有非单位元可以两两配对，于是$\vert G\vert =2n+1$.这与$\vert G\vert $为偶数矛盾.因此$G$中有二阶元.

$9$.证明$S_n =\langle (12),(13),\cdots ,(1n)\rangle $.

证明：$S_n $中每个置换可以表示成一些对换的乘积，又任一对换$(ij)$可以表示成

$$(ij)=(1i)(1j)(1i).$$

因此$S_n $可以由$\lbrace (12),(13),(14),\cdots ,(1n)\rbrace $生成，即

$$S_n =\langle (12),(13),\cdots ,(1n)\rangle .$$

$10$.证明$S_n =\langle (12),(123\cdots n)\rangle $.

证明：$1)\;$我们已证$S_n =\langle (12),(13),\cdots ,(1n)\rangle $，因此只要对于$k\in \lbrace 3,4,\cdots ,n\rbrace $，去证$(1k)$可以表示成$(12),(23),\cdots ,(n-1,n)$这些对换的乘积（它们可以重复出现）.

$$\begin{align}
(13) & =(23)(12)(23) , \\
(14) & =(34)(13)(34)=(34)(23)(12)(23)(34), \\
\cdots & \cdots \cdots \cdots \\
(1k) & =(k-1,k)(1,k-1)(k-1,k) \\
& =(k-1,k)(k-2,k-1)\cdots (34)(23)(12)(23)(34)\cdots (k-2,k-1)(k-1,k). \\
\end{align}$$

因此$S_n =\langle (12),(23),(34),\cdots ,(n-1,n)\rangle $.

$2)\;$根据$1)\;$，只要去证对于$k\in \lbrace 2,3,\cdots ,n-1\rbrace $，有$(k,k+1)$可以表示成$(1,2),(123\cdots n)$的整数次幂的乘积.

$$\begin{align}
(23) & =(123\cdots n)(12)(123\cdots n)^{-1} ,\\
(34) & =(123\cdots n)(23)(123\cdots n)^{-1} =(123\cdots n)^2(12)(123\cdots n)^{-2} , \\
\cdots & \cdots \cdots \cdots \\
(k,k+1) & =(123\cdots n)(k-1,k)(123\cdots n)^{-1} \\
& =(123\cdots n)^{k-1}(12)(123\cdots n)^{-(k-1)}. \\
\end{align}$$

因此$S_n =\langle (12) ,(123\cdots n)\rangle $.

$11$.证明交错群$A_n ,n\geq 3$，是由$3$循环生成的，并且事实上

$$A_n =\langle (123),(124),\cdots ,(12n)\rangle .$$

证明：$1)\;$由于任一偶置换可以表示成偶数个对换的乘积，且$S_n $可以由$(12),(13),(14),\cdots ,(1n)$生成，因此只要考察$(1i)(1j)$能写成什么形式.由于$(1i)(1j)=(1ji)$，因此每一个$n$元偶置换$(n\geq 3)$可以表示成一些$3-$轮换的乘积.从而$A_n $由$3-$轮换生成.

$2)\;$我们已证$A_n $可由$3-$轮换生成，因此只要去证任一$3-$轮换$(ijk)\in \langle (123),(124),\cdots ,(12n)\rangle $.

$$\begin{align}
(ijk) & =[(1i)(2j)] (12k)[(1i)(2j)]^{-1} ,\\
& =[(1i)(12)(21)(2j)] (12k)[(1i)(12)(21)(2j)]^{-1} \\
& =[(12i)(12j)] (12k)[(12i)(12j)]^{-1} .\\
\end{align}$$

因此$A_n =\langle (123),(124),\cdots ,(12n)\rangle $.

$12$.证明循环$\pi =(12\cdots n)\in S_n $的$k$次方幂${\pi }^k $是$d$个互不相交的循环的乘积，每一个的长度为$q=\dfrac{n}{d} $，其中$d=\mathrm{g.c.d} (n,k)$是$n$和$k$的最大公因数.

$13$.设置换$\pi \in S_n $，将$\pi $分解成互不相交的循环的乘积，证明$\pi $的阶（即循环子群$\langle \pi \rangle $的阶），等于这些循环的阶的最小公倍数.

$14$.设$A,B\in M_n (\mathbb{R} )$且$(AB)^m =E$对某个整数$m$成立，那么一定有$(BA)^m =E$吗？

解：设$A,B\in M_n (\mathbb{R} )$且$(AB)^m =E$对某个整数$m$成立，若$B$可逆，则

$$\begin{align}
(BA)^m & =(BA)(BA)\cdots (BA) \\
& =B(AB)(AB)\cdots (AB)A \\
& =B(AB)(AB)\cdots (AB)A E \\
& =B(AB)(AB)\cdots (AB)(A B)B^{-1} \\
& =BEB^{-1} \\
& =E .\\
\end{align}$$

$15$.设$G$是一个有限（乘法）群，$H$是$G$的一个非空子集，如果$H$关于$G$的乘法封闭，证明$H$是一个子群.事实上，在这种情况下，在$H$中存在单位元$e$和逆元$h^{-1},h\in H$的要求是多余的.

证明：对于群$G$的非空子集$H$，如果$H$关于$G$的乘法具有封闭性，则$H$是有限半群.由于消去律在群$G$中成立，在其子集合中当然成立.于是$H$是$G$的一个子群.

$16$.正有理数的乘法群$(\mathbb{Q}_+ ,\cdot )$可以有什么样的生成元集？

提示：利用第$1$章$\S 9$的算术基本定理.

在$(\mathbb{Q}_+ ,\cdot )$中是否存在有限生成元集？

$17$.证明对于给定的阶数$n$，在同构的意义下仅有有限多个$n$阶群，群的个数记作$\rho (n)$.

提示：估计上述$n$阶凯莱表的个数.运用定理$4$证明$\rho (n)$不会超过$\displaystyle {n! \choose n}$，即从$S_n $中取$n$个置换组成的不同子集的个数.事实上，$\rho (n)$远小于此数，但逼近于精确值的较好的估计至今没有找到.

$18$.用习题$10$证明，每个有限群都可以嵌入到具有两个生成元的有限群中（即存在到这种群内的一个单同态）.

$19$.试证图$17$标示出了交错群$A_4 $的所有子群.

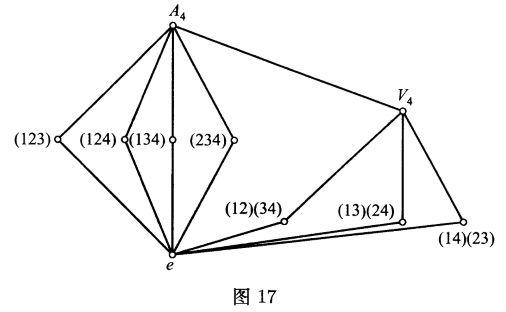
其中符号$V_4 $代表克莱因$4$元群，$V_4 =\lbrace e,(12)(34),(13)(24),(14)(23)\rbrace $，图中的其他顶点代表循环子群，其生成元已写明.

$20$.证明所有的$4$阶群都是阿贝尔群，精确到同构只有置换群$U=\langle (1234)\rangle $和克莱因四元群$V_4 $两种，也可以写成矩阵群：

$$L_1 =\left\lbrace \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} ,\begin{pmatrix} 0 & 1 \\ -1 & 0 \end{pmatrix} ,\begin{pmatrix} -1 & 0 \\ 0 & -1 \end{pmatrix} ,\begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix} \right\rbrace \subset \mathrm{GL}_2 (\mathbb{R} ) ,$$

$$L_2 =\left\lbrace \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} ,\begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} ,\begin{pmatrix} -1 & 0 \\ 0 & 1 \end{pmatrix} ,\begin{pmatrix} -1 & 0 \\ 0 & -1 \end{pmatrix} \right\rbrace \subset \mathrm{GL}_2 (\mathbb{R} ) .$$

给出同构映射$U\to L_1 ,V_4 \to L_2 $.

提示：若任取$x\in G$，有$x^2 =e$，则$abab=e\Rightarrow ab =b^{-1}a^{-1} =b(b^{-1})^2(a^{-1})^2 a=beea=ba$.