定义和例子

考察行列式不为$0$的实系数$n\times n$矩阵的集合${\rm GL }_n (\mathbb{R} ) $.根据第$3$章$\S 2$的定理$3$，$\det A\neq 0$，$\det B\neq 0\Rightarrow \det AB\neq 0$.我们看到，$A,B\in {\rm GL }_n \Rightarrow AB\in {\rm GL}_n (\mathbb{R} )$.进一步，$(AB)C=A(BC)$，并且存在一个矩阵$E$，使得对一切$A\in {\rm GL}_n (\mathbb{R} ) $，$AE=EA=A$.此外，任意矩阵$A\in {\rm GL}_n (\mathbb{R} )$都有“逆元”，即逆矩阵$A^{-1}$，使得$AA^{-1} =A^{-1}A=E$.

集合${\rm GL}_n (\mathbb{R} )$连同合成法则（二元运算）$(A,B)\mapsto AB$称为$\mathbb{R} $上的$n$阶一般线性群，沿用$\S 1$的术语，它是幺半群$(M_n (\mathbb{R} ) ,\cdot ,E)$中的所有可逆元素构成的子幺半群.但是这个子幺半群特别重要，它得到了特殊的命名，并成为一般理论有价值的实例.

定义$\quad $所有的元素都可逆的幺半群叫作群.换言之，下述公理必须满足.

${\rm G0})$在集合$G$上定义了一个二元运算$(x,y)\mapsto xy$.

${\rm G1})$运算是结合的：任取$x,y,z\in G,(xy)z=x(yz)$.

${\rm G2})\;G$有单位元$e$：任取$x\in G,xe =ex=x$.

${\rm G3})\; G$的任意元素$x$有逆元$x^{-1} $：$xx^{-1} =x^{-1} x=e$.

我们在第$1$章$\S 8$中引出的代数结构$S_n $满足上述公理，称之为$n$元置换的对称群.事实上，正是这些重要的例子，使我们想到了群的一般定义.

令人惊讶的是，代数学中最古老和结果最丰富的领域，竟然建立在这样的一组简单的公理之上，这一领域在几何学中，以及将数学应用到自然科学当中发挥着根本作用.稍加分析可见，它们还可以进行简化，但这种事对于我们来说不是原则性的.

带有交换二元运算的群自然叫作交换群，也常常叫作阿贝尔群（为了纪念挪威数学家阿贝尔）.“群”这一术语是由群论的创始人，法国数学家伽罗瓦引入的.群论的思想在伽罗瓦之前已有流传（就像基本的数学思想产生时常有的那样），拉格朗日实际上已经证明了群论的一些定理，虽然其形式是朴素的.伽罗瓦天才的工作起初并没有被人们理解，对这一工作重又引起兴趣是在若尔当的书《置换与代数方程》-（$1870$年）出版之后开始的.直到$19$世纪末，群论才“完全脱离了梦幻，代之以精细整理过的逻辑结构.”（克莱因，《19世纪数学发展史讲义》）.

对于群$G$中元素的个数（更准确地说，群的基数），可用等价的符号${\rm Card}\;G,\vert G\vert $以及$(G\colon e)$表示.当然在$\S 1$中关于幺半群的全部论述都可以用到群上来.仅需引入一些必要的新名词.特别是，子集$H\subset G$称为$G$的一个子群，若$e\in H$；$h_1 ,h_2 \in H\Rightarrow h_1 h_2 \in H$；且$h\in H\Rightarrow h^{-1} \in H$.子群$H\subset G$叫作一个真子群，若$H\neq \lbrace e\rbrace $，且$H\neq G$.

我们再给出一些群的例子.

例1$\quad $在一般线性群${\rm GL}_n (\mathbb{R} )$中考察由行列式为$1$的矩阵构成的子集${\rm SL}_n (\mathbb{R} )$：

$${\rm SL}_n (\mathbb{R} )=\lbrace A\in {\rm GL}_n (\mathbb{R} )\vert \det A=1\rbrace .$$

显然，$E\in {\rm SL}_n (\mathbb{R} )$.根据第$3$关于行列式的一般结果

$$\det A=1,\det B=1\Rightarrow \det AB=1,$$

$$\det A^{-1} =(\det A)^{-1} =1.$$

所以${\rm SL}_n (\mathbb{R} )$是${\rm GL}_n (\mathbb{R} )$的一个子群；称为$\mathbb{R}$上的$n$阶特殊线性群.它也叫作单位模群，然而后一名词通常用于行列式为$\pm 1$的矩阵构成的群.

应该指出，群${\rm GL}_n (\mathbb{R} )$中包含着许多有趣的群，几代数学家都把它看作新的思想和未解决问题的无尽的源泉.

例2$\quad $用有理数代替实数，我们就得到了$\mathbb{Q}$上的$n$阶一般线性群${\rm GL}_n (\mathbb{Q} )$及其子群${\rm SL}_n (\mathbb{Q} )$，在群${\rm SL}_n (\mathbb{Q} )$中包含一个有趣的子群${\rm SL}_n (\mathbb{Z} )$，它由行列式为$1$的整数矩阵组成.第$3$章$\S 3$的定理$1$给出了其逆矩阵的表达式，由此可以证明，${\rm SL}_n (\mathbb{Z} )$确实是一个子群.群${\rm SL}_n (\mathbb{Q} )$和${\rm SL}_n (\mathbb{Z} )$在数论中占有重要的地位.在图$15$中，${\rm GL}_n (\mathbb{R} )$的上述子群构成了一个偏序集（见第$1$章$\S 6$第$4$章）.

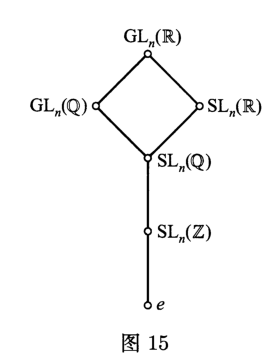
例3$\quad $令例$1$和例$2$中的$n=1$，我们得到了实数和有理数上的$1$阶乘法群

$$\mathbb{R} ^{\ast } =\mathbb{R} \setminus \lbrace 0\rbrace ={\rm GL}_1 (\mathbb{R} ),\quad \mathbb{Q} ^{\ast } =\mathbb{Q} \setminus \lbrace 0\rbrace ={\rm GL}_1 (\mathbb{Q} ).$$

这些群显然是无限的.因为在$(\mathbb{Z} ,\cdot ,1)$中的可逆元仅有$1$和$-1$，故${\rm GL}_1 (\mathbb{Z} )=\lbrace \pm 1\rbrace $.进一步，${\rm SL}_1 (\mathbb{R} )={\rm SL}_1 (\mathbb{Q} )=$ ${\rm SL}_1 (\mathbb{Z} )=1$.但当$n=2$时，甚至连群${\rm SL}_2 (\mathbb{Z} )$都是无限的.比如：它包含所有的矩阵

$$\begin{pmatrix} 1 & m \\ 0 & 1 \end{pmatrix} ,\begin{pmatrix} 1 & 0 \\ m & 1 \end{pmatrix} ,\begin{pmatrix} m & m-1 \\ 1 & 1 \end{pmatrix} ,m\in \mathbb{Z} .$$

我们进一步指出若干无限加群：

$$(\mathbb{R} ,+,0),(\mathbb{Q} ,+,0),(\mathbb{Z} ,+,0).$$

例4$\quad $设$\Omega $是任意集合，而$S(\Omega )$是全体双射（一一映射）$f\colon \Omega \to \Omega $的集合.考虑到第$1$章$\S 5$关于集合的映射的结果（定理$1$，定理$2$以及定理$2$的推论），我们马上断言，$S(\Omega )$是一个群，其自然的二元运算是映射的合成.自然地，$S(\Omega )$是$\S 1$例$1$中定义的幺半群$M(\Omega )$的子幺半群，它由$M(\Omega )$的全体可逆元素组成，但这个细节我们就不过多强调了.群$S(\Omega )$自身，特别是它的各类子群叫作变换群，它们在群论的各种应用中是很基础的.$1872$年克莱因宣布了著名的“爱尔兰根纲领”，将变换群的概念作为对各种几何学进行分类的基础（关于这一点详见[${\rm BA}\;Ⅱ$]）.

如果将$\Omega $取作线性空间$\mathbb{R} ^n$，我们就得到了一个“很大”的难以全面认识的群$S(\mathbb{R} ^n)$.但$S(\mathbb{R} ^n)$中包含一个由可逆线性变换${\varphi}_A \colon \mathbb{R} ^n \to \mathbb{R} ^n $构成的子群，它与$n$阶非退化矩阵$A$一一对应（见第$2$章$\S 3$）.

这样就可以把${\rm GL}_n (\mathbb{R} )$嵌入到$S(\mathbb{R} ^n)$中.

在下面引入群同构的重要概念之后，这一嵌入的含义就清楚了.

循环群

设$G$是乘法群（即带有乘法运算），$a$是$G$的一个取定的元素.如果任意元素$g\in G$都可以写成$g=a^n$的形式，其中$n\in \mathbb{Z}$，则称$G=\langle a\rangle $是带有生成元$a$的循环群（或由元素$a$生成的循环群）.类似地，在加法的情况下，循环群定义成$\langle a\rangle =\lbrace na\vert n\in \mathbb{Z} \rbrace $.当然，这并不意味着元素$a^n $或$na$是两两不同的.约定符号$(a^{-1})^k =a^{-k}$，并证明下述论断的正确性.

定理1$\quad $任取$m,n\in \mathbb{Z} $，

$$a^m a^n=a^{m+n} ,\quad (a^m)^n =a^{mn} $$

（对应地，$ma+na=(m+n)a,n(ma)=(nm)a$）.

证明$\quad $如果$m,n$是非负的，见$\S 1$第$3$段的关系式$(2)$和$(2’)$.如果$m < 0 ,n < 0$，则$m’=-m > 0$，$n’=-n > 0$，且

$$a^m a^n =(a^{-1})^{m’} (a^{-1})^{n’} =(a^{-1})^{m’+n’} =a^{-(m’+n’)} =a^{m+n} .$$

如果$m’=-m > 0$，则有

$$a^m a^n =(a^{-1})^{m’} a^n =(\underbrace{a^{-1} \cdots a^{-1} }_{m’} )(\underbrace{a\cdots a}_{n} )=a^{n-m’}=a^{m+n} .$$

如果$m’\geq n$，则

$$a^{n-m’} =(a^{-1})^{m’-n} =a^{m+n} .$$

当$m > 0,n < 0$时，可类似处理.利用上述论断和元素方幂的定义，易证等式$(a^m)^n =a^{mn} $.$\quad \quad \square $

循环群最简单的例子是整数加群$(\mathbb{Z} ,+,0)$，它由元素$1$或$-1$生成.易验证矩阵$\begin{pmatrix} 1 & 1 \\ 0 & 1 \end{pmatrix}$生成${\rm SL}_2 (\mathbb{Z} )$的一个无限循环子群.集合$\lbrace 1,-1\rbrace $是一个$2$阶的乘法循环群.

我们来看$n$阶循环群的一个例子，考察平面绕某个点$O$的旋转，使得中心在$O$点的任意正$n$边形$P_n $变到自身.显然，这些旋转构成一个群：它的乘法是将两个旋转依次旅行.我们的群$C_n $含有旋转${\varphi }_0 ,{\varphi }_1 ,\cdots ,{\varphi }_{n-1}$，它们分别是依逆时针方向旋转角度$0,\dfrac{2\pi }{n} ,\cdots ,\dfrac{(n-1)2\pi }{n} $.这时${\varphi }_s ={\varphi }_1^s $，从几何直观出发，显然有${\varphi }_s^{-1} ={\varphi }_1^{n-s} $，且${\varphi }_1^n ={\varphi }_0 $（单位变换）.于是$\vert C_n \vert =n$且$C_n =\langle {\varphi }_1 \rangle $.注意循环群$C_n $是正$n$边形$P_n $的全体对称变换（即$P_n $到自身的变换）$D_n $的一个真子群.

再一次假定$G$是任意群，$a$是$G$的一个元素.我们得到了两种可能性.

$1)\;$元素$a$的所有方幂两两不同，即$m\neq n\Rightarrow a^m \neq a^n$.这时称元素$a$是一个无限阶元.

$2)\;$当$m\neq n$时，有等式$a^m =a^n$.如果$m > n$，则$a^{m-n} =e$，即元素$a$的某个正方幂等于$G$的单位元.设$q$是使$a^q =e$的最小正数，这时我们称元素$a$是有限阶元，阶数为$q$.

在一个有限群$G({\rm Card} \; G < \infty )$中，自然所有的元素都是有限阶的.

注意“阶”这个词在数学中有多种含义.我们以前谈过$n$阶方阵（即$n\times n$阶的矩阵），但一个非退化矩阵$A$作为${\rm GL}_n (\mathbb{R} )$的元素也有在刚才指出的意义下的一个阶（可能是无限的）.但从上下文看，每一次出现的阶的含义都是清楚的.

回顾$n$阶循环群，下述论断几乎是显然的.

定理2$\quad $任意元素$a\in G$（这里$G$是任意的群）的阶等于${\rm Card}\langle a\rangle $.

如果$a$是一个$q$阶元，则$\langle a\rangle =\lbrace e,a,\cdots ,a^{q-1} \rbrace $，

$$a^k =e\Leftrightarrow k=lq ,\quad l\in \mathbb{Z} .$$

证明$\quad $如果$a$是无限阶元，无需证明.如果$a$是$q$阶元，则由定义，元素$e,a,a^2 ,\cdots ,a^{q-1} $两两不同.任意其他的方幂$a^k$与这些元素之一重合，即$\langle a\rangle =\lbrace e,a,\cdots ,a^{q-1} \rbrace $.为此，利用$\mathbb{Z}$中的带余除法（第$1$章$\S 9$第$3$段），将$k$写成如下形式

$$k=lq+r,\quad 0\leq r\leq q-1$$

运用定理$1$给出的方幂法则，得到

$$a^k =(a^q)^l a^r =ea^r =a^r .$$

特别地，$a^k=e\Rightarrow r=0\Rightarrow k=lq$.

同构

前面已经指出，沿逆时针方向旋转$0^{\circ } ,120^{\circ },240^{\circ }$的三个旋转${\varphi }_0 ,{\varphi }_1 ,{\varphi }_2 $将等边三角形$P_3 $变到自身.但是还有图$16$指出的三个轴对称变换（反射）${\psi }_1 ,{\psi }_2 ,{\psi }_3 $.它们的对称轴分别是$1-1’,2-2’,3-3’$.全体$6$个对称变换分别对应于三角形顶点集的六个置换.我们得到

$$\begin{array}{lll}
{\varphi }_0 \sim e, & {\varphi }_1 \sim (123), & {\varphi }_2 \sim (132),\\
{\psi }_1 \sim (23), & {\psi }_2 \sim (13), & {\psi }_3 \sim (12).\\
\end{array}$$

因为不再有其他的三元置换，故可断言，正三角形的全体对称变换组成的群$D_3$显示出与对称群$S_3$的极大类似.

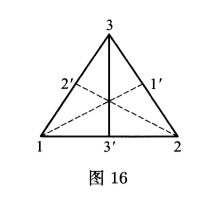
在同样的意义下，循环群$G_n $（见第$2$节例）$\langle (1\;2\; \cdots \;n)\rangle \subset S_n $彼此相似.这些事实和关于群的一般性思考，引出了一个十分自然的问题，它涉及群的最本质的属性.初看起来，一个群$G$的全部信息已包含在$G$的乘法表中，称之为凯莱表：

$$
\begin{array}{c|ccccc}
& g_1 & g_2 & \cdots & g_n & \cdots \\
\hline
g_1 & g_1 g_1 & g_1 g_2 & \cdots & g_1 g_n & \cdots \\
g_2 & g_2 g_1 & g_2 g_2 & \cdots & g_2 g_n & \cdots \\
\cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\
g_n & g_n g_1 & g_n g_2 & \cdots & g_n g_n & \cdots \\
\cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\
\end{array}
$$

事实上，群的很多规律可以从观察它的凯莱表得出，即从以$m_{ij} =g_i g_j \in G$为元素的矩阵$M=(m_{ij} )$得出（若$n=(G\colon e)$，矩阵的阶为$n\times n$）.例如，我们注意到在矩阵$M$的每一行和每一列，群$G$的任意元素刚好出现一次（见下述定理$4$的证明）.群$G$是阿贝尔群当且仅当矩阵$M$是对称的，即$m_{ij} =m_{ji}$.可以从表中得到的群的性质有很多，但是毕竟在比较两个群$G$与$G’$的乘法表时，涉及元素的排列顺序，因为矩阵$M$的形状依赖于群元素的取法，而在无限群的情形，情况就更加复杂.

比较群$G$与$G’$的最正确最基本的方法基于同构的概念.

定义$\quad $两个分别具有运算$\ast $与$\circ $的群$(G,\ast )$与$(G’,\circ )$称为同构的，若存在一个映射$f\colon G\to G’$，使得

$i)\; f(a\ast b)=f(a)\circ f(b)$对任意$a,b\in G$成立；

$ii)\; f$是双射.

通常用符号$G\simeq G’$表示两个群同构.

我们给出同构的一些简单性质.

$1)\;$单位元对应到单位元.$\quad $事实上，若$e$是群$G$的单位元，则$e\ast a=a\ast e=a$，这就意味着$f(e)\circ f(a)=f(a)\circ f(e)=f(a)$，因而$f(e)=e’$是群$G’$的单位元.这一证明部分地用到了$f$的两个性质.性质$i)$是显然的，性质$ii)$保证了$f$是满射，因而$f(g)$取遍了群$G’$的所有元素.

$2)\; f(a^{-1})=f(a)^{-1}$.事实上，根据$1)\;f(a)\circ f(a^{-1})=f(a\ast a^{-1})=f(e)=e’$是$G’$的单位元，从而

$$\begin{align}
f(a)^{-1} & =f(a)^{-1} \circ e’=f(a)^{-1} \circ (f(a)\circ f(a^{-1})) \\
& = (f(a)^{-1} \circ f(a)) \circ f(a^{-1}) =e’\circ f(a^{-1}) =f(a^{-1}) .\\
\end{align}$$

$3)\;$逆映射$f^{-1} \colon G’\to G$（根据性质$ii)$，$f^{-1}$是存在的）也是一个同构.由于第$1$章$\S 5$定理$2$的推论，我们仅需验证$f^{-1}$满足性质$i)$.设$a’,b’\in G$.由于$f$的双射性有$a,b\in G$，使$f(a)=a’,f(b)=b’$.因为$f$是同构，$a’\circ b’=f(a)\circ f(b)=f(a\ast b)$.从而有$a\ast b=f^{-1} (a’\circ b’)$，又因为$a=f^{-1} (a’),b=f^{-1} (b’)$，故$f^{-1} (a’\circ b’)=f^{-1} (a’) \ast f^{-1} (b’)$.

注记$\quad $简单的验证表明，在群$D_3 $和$S_3 $之间建立的关系$\sim $是一个同构.

函数$f\colon =\ln $是正实数乘法群$({\mathbb{R} }_+ ,\cdot )$到全体实数的加法群$(\mathbb{R} ,+)$的一个同构映射.显然对数函数的性质$\ln ab=\ln a+\ln b$恰为同构定义中的性质$i)$的一个模型.$f$的逆映射是指数函数$x\mapsto e^x $.

现在我们来证明两个一般性的定理，说明同构在群论中的作用.

定理3$\quad $任意两个同阶的循环群是同构的（特别地，任意两个无限循环群是同构的）.

证明$\quad $事实上，若$\langle g\rangle $是无限循环群，则所有的$g$的方幂$g^n$是彼此不同的，令$g^n \mapsto f(g^n)=n$.我们得到了一个同构$f\colon \langle g\rangle \to (\mathbb{Z} ,+)$.$f$的双射性是显然的，而性质$f(g^m g^n)=f(g^m)+f(g^n)$由定理$1$推出.

现在设$G=\lbrace e,g,\cdots ,g^{q-1} \rbrace $，$G’=\lbrace e’,g’,\cdots ,(g’)^{q-1} \rbrace $是两个$q$阶循环群（$G$和$G’$中的运算均用乘法表示）.我们定义一个一一映射

$$f\colon g^k \mapsto (g’)^k ,\quad k=0,1,\cdots ,q-1.$$

任取$n,m=0,1,\cdots ,q-1$，设$n+m=lq+r,0\leq r\leq q-1$，如同定理$2$的证明，我们有

$$f(g^{n+m})=f(g^r)=(g’)^r=(g’)^{n+m}=(g’)^n(g’)^m=f(g^n)f(g^m).$$

定理4（凯莱）$\quad $任意$n$阶有限群都同构于对称群$S_n $的某个子群.

证明$\quad $设$G$是我们的群，$n=\vert G\vert $.可以将$S_n $看作集合$G$到自身的全体一一映射的集合，因为被$S_n $的置换所作用的那些元素，其自然属性是非本质的.

对于任意元素$a\in G$，我们来看由公式

$$L_a (g)=ag$$

定义的映射$L_a \colon G\to G$（显然我们重述了第$1$章$\S 8$第$3$段的定义）.如果$e=g_1 ,g_2 ,\cdots ,g_n $是群$G$的全部元素，那么$ag_1 ,ag_2 ,\cdots ,ag_n $是按照另外的次序排列的$G$的全部元素（回忆凯莱表）.这件事是明显的，因为

$$ag_i =ag_j \Rightarrow a^{-1}(ag_i )=a^{-1}(ag_j ) \Rightarrow (a^{-1}a)g_i =(a^{-1}a)g_j \Rightarrow g_i =g_j .$$

显然，$L_a $是一个双射（置换），其逆映射为$L_a^{-1} =L_{a^{-1} }$.恒等映射自然是$L_e$.

再一次运用$G$中乘法的结合律，得到$L_{ab} (g)=(ab)g=a(bg)=L_a (L_b g)$，即$L_{ab} =L_a L_b $.

令$S(G)$是集合$G$到自身的全体双射组成的群，即群$S_n $，则集合$L_e ,L_{g_2 } ,\cdots ,L_{g_n }$构成$S(G)$的一个子群$H$.我们有包含关系$H\subset S_n $和对应关系$L\colon a\mapsto L_a \in H$，根据上面的论述，$L$具有同构的一切性质.

凯莱定理虽然简单，但在群论中意义重大.它引出了某种“通用”对象（对称群$\lbrace S_n \vert n=1,2,\cdots \rbrace $的族），这种通用对象在精确到同构的意义下包含了所有的一般有限群.短语“精确到同构”，即将所有同构的群归为一类，不仅反映出群论的本质也反映出整个数学的本质，没有这样的一般化，数学就失去了意义.

在同构的定义中若$G’=G$，我们就得到了群$G$到自身的同构映射$\varphi \colon G\to G$.称之为群的自同构.例如恒等映射$e_G \colon g\mapsto g$（以后简记作$1$）是自同构，但一般来说，群$G$也有非平凡自同构.同构映射的性质$3)$表明，自同构的逆映射也是自同构.如果$\varphi ,\psi $是群$G$的自同构，那么任取$a,b\in G$，$(\varphi \circ \psi )(ab)=\varphi (\psi (ab))=\varphi (\psi (a)\psi (b))=(\varphi \circ \psi )(a)(\varphi \circ \psi )(b)$.事实上，群$G$的全体自同构的集合$\mathrm{Aut} (G)$构成$S(G)$的一个子群，后者由$G\to G$的全体双射组成.

同态

在群$G$的自同构群中含有一个特殊的子群.它用符号$\mathrm{Inn} (G)$表示，称为内自同构群.其元素是映射

$$I_a \colon g\mapsto aga^{-1} .$$

简单的练习表明，$I_a $满足自同构的一切性质，并且$I_a^{-1} =I_{a^{-1} }$，$I_e =1$是单位自同构，$I_a \circ I_b =I_{ab}$（因为$(I_a \circ I_b )(g)=I_a (I_b (g))=I_a (bgb^{-1})=abgb^{-1}a^{-1} =(ab)g(ab)^{-1}=I_{ab} (g)$）.

最后一个关系式指出，由公式$f(a)=I_a ,a\in G$，定义的从群$G$到它的内自同构群$\mathrm{Inn} (G)$的映射

$$f\colon G\to \mathrm{Inn} (G)$$

满足自同构映射的性质$i)\colon f(a)\circ f(b)=f(ab)$.但性质$ii)$不一定满足.例如，当$G$是阿贝尔群时，任取$a,g\in G$，$aga^{-1} =g$，故$I_a =I_e $，群$\mathrm{Inn} (G)$仅由单位元$I_e $组成.这个例子自然导致了下述的一般化

定义$\quad $群$(G,\ast )$到$(G’,\circ )$的一个映射$f\colon G\to G’$叫作同态映射，若

$$\forall a,b\in G,\quad f(a\ast b)=f(a)\circ f(b)$$

（换言之，只满足同构定义中的性质$i)$）.

集合

$$\mathrm{ker} f=\lbrace g\in G\vert f(g)=e’,其中e’是G’的单位元\rbrace ,$$

叫作同态$f$的核.

群到自身的同态映射也叫作群的自同态.

在同态的定义中不仅不要求$f$是单射，也不要求$f$是满射（即“到上”的映射），但这不是本质的，因为我们总可以局限于考察映射的像$\mathrm{Im} f\subset G’$，它显然是$G’$的一个子群.同态$f$与同构的主要区分点在于非平凡核$\mathrm{ker} f$的存在性，它是度量$f$的非单射性的尺度.如果$\mathrm{ker} f=\lbrace e\rbrace $，则$f\colon G\to \mathrm{Im} f$是一个同构.

我们指出

$$f(a)=e’,f(b)=e’\Rightarrow f(a\ast b)=f(a)\circ f(b)=e’\circ e’=e’,$$

且

$$f(a^{-1})=f(a)^{-1} =(e’)^{-1}=e’.$$

所以核$\mathrm{ker} f$是$G$的一个子群.

术语.例子

术语满射（“到上”的映射），单射（嵌入映射），双射（一一映射），可用于任意集合间的映射（不一定有运算），在讨论群（或其他代数系统）时，我们使用相应的术语满同态（“到上”的同态），单同态（带有单位核的同态），同构（一一同态，既满且单）.存在着用态射取代同态的倾向.在阅读数学文献时了解这些术语是有用的，但最初读者（如果愿意）可以在术语同构与同态之前附加“映入”和“映上”等字样.

现在来进一步考察群同态的若干例子.

例5$\quad $整数加群$\mathbb{Z} $到$q$阶循环群$\langle g\rangle $上有一个满同态$f\colon n\mapsto g^n $（见$\S 2$定理$2$）.此时，显然有$\mathrm{ker} f=\lbrace lq\vert l\in \mathbb{Z} \rbrace $.事实上，$\lbrace lq \rbrace \subset \mathrm{ker} f$是显然的，反面的包含关系从定理$1$得到.

例6$\quad $从实数加群$\mathbb{R} $到平面绕不动点$O$点的旋转群$T$的映射$f\colon \mathbb{R} \to T$由公式$f(\lambda )={\Phi }_{\lambda }$给出（此处${\Phi }_{\lambda }$是逆时针转过角度$2\pi \lambda $的旋转），它是一个同态，理由是${\Phi }_{\lambda } \circ {\Phi }_{\mu } ={\Phi }_{\lambda +\mu }$.旋转$2\pi $的整倍数与单位旋转（转零角度）重合，故$\mathrm{ker} f=\mathbb{Z} $.也可以说$f$是$\mathbb{R} $到单位圆周上的一个同态，因为在${\Phi }_{\lambda } $与单位圆周$S^1 $的点之间存在由一个极坐标$(1,2\pi \lambda )$给出的一一对应，其中$0\leq \lambda < 1$.

例7$\quad $一般线性群${\mathrm{GL}}_m (\mathbb{R} )$由满足$\det A\neq 0$的$m\times m$实矩阵$A$构成，令$f\colon =\det $则有从${\mathrm{GL}}_m (\mathbb{R} )$到非零实数乘法群${\mathbb{R} }^{\ast }$上的同态.同态条件$f(AB)=f(A)f(B)$恰为第$3$章$\S 2$定理$3$的公式.根据定义${\mathrm{SL}}_m (\mathbb{R} )=\mathrm{ker} f$.

例8$\quad $考察$2$阶循环群$C_2 =\langle -1\rangle =\lbrace 1,-1\rbrace $.如果必要，它可以用凯莱表抽象地给出：

$$
C_2 \colon \quad \begin{array}{c|cc}
\cdot & 1 & -1 \\
\hline
1 & 1 & -1 \\
-1 & -1 & 1 \\
\end{array}
$$

由已知的函数$\varepsilon =\mathrm{sgn} \colon \pi \mapsto {\varepsilon }_{\pi } $（置换$\pi $的符号）给出的映射$\varepsilon \colon S_n \to C_2 $是对称群$S_n $到$C_2 $上的同态.核$\mathrm{ker} \varepsilon =A_n $，阶为$\dfrac12 n!$（见第$1$章$\S 8$第$3$段），$A_n $叫作交错群.

例9$\quad $无限群可以同构于自己的真子群.例如加法群$(\mathbb{Z} ,+)$包含有真子群$n\mathbb{Z} =\lbrace nk\vert k\in \mathbb{Z} \rbrace $，其中$n > 1$是一个固定整数.易验证由$g_n (k)=nk$定义的映射$g_n \colon \mathbb{Z} \to n\mathbb{Z} $是一个同构.顺便指出，$\mathbb{Z} $和$n\mathbb{Z} $都是无限循环群，生成元分别为$1$或$-1$，以及$n$或$-n$；所以$g_n $和映射$k\mapsto -nk $是$\mathbb{Z} \to n\mathbb{Z} $的全部可能的同构映射.

例10$\quad $群$\mathrm{Aut} (G)$，甚至个别的一个非单位元$\varphi \in \mathrm{Aut} (G)$，都可能带来群$G$的重要信息.下面的例子可以说明这一点.设$G$是有限群，它有一个$2$阶自同构$\varphi (\varphi ^2 =1)$，没有非平凡的不动点：

$$a\neq e\Rightarrow \varphi (a)\neq a.$$

设$\varphi (a)a^{-1} =\varphi (b)b^{-1} $对任意$a,b\in G$成立.对等式左乘$\varphi (b)^{-1} $，右乘$a$，得到$\varphi (b)^{-1} \varphi (a)=b^{-1} a$，即$\varphi (b^{-1} a)=b^{-1} a$，从而$b^{-1} a=e,b=a$.也就是说，当$a$取遍$G$的所有元素时，$\varphi (a)a^{-1}$亦然，或等价说，任意元素$g\in G$可以写成$g=\varphi (a)a^{-1} $的形式.但这时$\varphi (g)=\varphi (\varphi (a))\varphi (a^{-1}) =\varphi ^2 (a)\varphi (a^{-1})=a\varphi (a)^{-1} =(\varphi (a)a^{-1})^{-1} =g^{-1} $.即$\varphi $重合于映射$g\mapsto g^{-1} $.由此得到$ab=\varphi (a^{-1}) \varphi (b^{-1})=\varphi (a^{-1}b^{-1})=(a^{-1}b^{-1})^{-1} =ba$，即$G$是阿贝尔群.此外$(G\colon e)$是一个奇数，因为$G$是由$e$和互不相同的元素对$g_i ,g_i^{-1} =\varphi (g_i )$组成的.

例11$\quad $下述例子表明，可以改变群的运算，但在同构的意义下不改变群自身，（亦见$\S 1$习题$3$）.设$G$是任意群，$t$是$G$的一个给定的元素.赋予集合$G$一个新的运算

$$(g,h)\mapsto g\ast h=gth.$$

我们可以直接验证$(g_1 \ast g_2 )\ast g_3 =g_1 \ast (g_2 \ast g_3 )$，即运算$\ast $是结合的.此外$g\ast t^{-1} =t^{-1} \ast g=g$，且$g\ast (t^{-1}g^{-1}t^{-1}) =(t^{-1}g^{-1}t^{-1})\ast =t^{-1}$，这就表明$(G,\ast )$是带有单位元$e_{\ast } =t^{-1}$的群.$g$在$(G,\ast )$中的逆元由$g_{\ast }^{-1} =t^{-1}g^{-1}t^{-1}$给出.映射$f\colon g\mapsto gt^{-1}$建立了群$(G,\cdot )$与$(G,\ast )$之间的同构，即$f(gh)=f(g)\ast f(h)$.

上述所有的例子都说明了一个一般性的原则：对群$G$的态射的研究反映出群$G$自身的重要信息.