在本章中将考察一些非常具体的代数系统，虽然我们在初等数学中已对它们有所了解，但仍然值得在这里作进一步的研究.上一章的观点使我们对早期传统的代数领域产生了新的看法.与此同时，多项式的例子使环的扩张以及在整环（整区）中因子分解的唯一性更好理解且易于把握.

数学史表明，“虚”数的拥挤者和反对者之间曾进行过长期的争论，该数来自代数方程

$$x^2+1=0.\label{1} \tag{1} $$

可以简单地约定方程$\eqref{1} $的解形式地记作$\pm \sqrt{-1} $，但更深远的问题是，赋予这一记法以某种意义.我们将在不同的层次上解决这一问题.先提出几个富有启发性的设想.

辅助结构

我们希望将实数域$\mathbb{R} $进行扩张，使得方程$\eqref{1} $在新的域中有解.形如

$$\begin{pmatrix} a & b \\ -b & a \end{pmatrix} \in M_2 (\mathbb{R} ) \label{2} \tag{2} $$

的全体二阶方阵的集合$P$可作为这种扩张的一个模型.我们断言，$P$是一个域（比较第$4$章$\S 3$习题$11$）.

事实上，$P$包含有环$M_2 (\mathbb{R} )$的零元（零矩阵）和单位元（单位矩阵$E$）.其次，从关系式

$$\begin{align}
\begin{pmatrix} a & b \\ -b & a \end{pmatrix} +\begin{pmatrix} c & d \\ -d & c \end{pmatrix} & =\begin{pmatrix} a+c & b+d \\ -(b+d) & a+c\end{pmatrix} ,\\
-\begin{pmatrix} a & b \\ -b & a \end{pmatrix} & =\begin{pmatrix} -a & -b \\ -(-b) & -a \end{pmatrix} ,\\
\begin{pmatrix} a & b \\ -b & a \end{pmatrix} \begin{pmatrix} c & d \\ -d & c \end{pmatrix} & =\begin{pmatrix} ac-bd & ad+bc \\ -(ad+bc) & ac-bd\end{pmatrix} ,\\
\end{align} \label{3} \tag{3} $$

得到，$P$关于加法和乘法运算封闭.这两种运算的结合性是它们在$M_2 (\mathbb{R} )$中结合性的推论.分配律和加法的交换性可同样得到.这样$P$是$M_2 (\mathbb{R} )$的一个子环.$P$中乘法的交换性由公式$\eqref{3} $的$3$式保证，最后只需证明若$P$中任意形如$\eqref{2} $的矩阵带有非零行列式$a^2+b^2\neq 0$，则在$P$中有逆矩阵.

可以利用求逆矩阵的公式（见第$3$章$\S 3$定理$1$）直接计算，也可以根据条件

$$\begin{pmatrix} a & b \\ -b & a \end{pmatrix} \begin{pmatrix} x & y \\ -y & x \end{pmatrix} =\begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}$$

列出线性方程组

$$ax-by=1,$$

$$bx+ay=0,$$

求解后得到

$$\begin{pmatrix} a & b \\ -b & a \end{pmatrix} ^{-1} =\begin{pmatrix} c & d \\ -d & c \end{pmatrix} ,\label{4} \tag{4} $$

其中$c=\dfrac{a}{a^2+b^2} ,d=\dfrac{-b}{a^2+b^2} $.

运用第$2$章$\S 3$数与矩阵相乘的公式$\eqref{5} $，我们将域$P$的任意元素写成如下形式：

$$\begin{pmatrix} a & b \\ -b & a \end{pmatrix} =aE+bJ,a,b\in \mathbb{R} ,J=\begin{pmatrix} 0 & 1 \\ -1 & 0 \end{pmatrix} .\label{5} \tag{5} $$

域$P$包含有子域$\lbrace aE\vert a\in \mathbb{R} \rbrace \cong \mathbb{R} $，而关系式

$$J^2+E=0$$

指出，元素$J\in P$“精确到同构”是，方程$\eqref{1} $的解，因而此处无需神秘地将$J$当作“虚构的量”.

但称为复数域的并不是域$P$，而是一个同构于$P$，其元素等同于平面上的点的域.希望域$P$有几何实现不是偶然的，在我们的心目中实数域$\mathbb{R} $与“实直线”密不可分，实直线上有一个定点表示$0$，并有一个单位长度用于确定$1$的位置.

复平面

于是，我们希望构造一个域$\mathbb{C} $，其元素是实平面$\mathbb{R}^2 $上的点，点的加法和乘法满足域的运算域，并使方程$\eqref{1} $在其中可解.取笛卡儿平面上的直角坐标系，$x$轴是横轴，$y$轴是纵轴.记$(a,b)$为横坐标为$a$，纵坐标为$b$的点.任取点$(a,b),(c,d)$如下定义它们的和与积

$$\begin{align}
(a,b)+(c,d) & =(a+b,c+d), \\
(a,b)(c,d) & =(ac-bd,ad+bc),\\
\end{align} \label{6} \tag{6} $$

（仍然用实数域$\mathbb{R} $中的记号$+,\cdot $，应该不至引起混淆）.直接但乏味的验证使我们确信，给定的运算使有序对（平面上的点）的集合构成了一个域.幸运的是，我们无需做这样的验证.将平面$\mathbb{C} $上的点对应到前面构造的域$P$的元素

$$(a,b)\mapsto \begin{pmatrix} a & b \\ -b & a \end{pmatrix} ,$$

公式$\eqref{3} $和$\eqref{6} $确保我们得到了一个同构，从而集合$\mathbb{C}$是一个域.通常称之为复数域.由于该域的几何实现，$\mathbb{C} $也叫作复数平面（更经常地叫作复平面）.

横轴，即$(a,0)$的集合与实直线有相同的性质，可设$(a,0)=a$.域的零元$(0,0)$和单位元$(1,0)$与通常实数的零元和单位元一致.纵轴上的点$(0,1)$处欧拉和高斯的时代起便记作$i$，称之为“虚数单位”，它是方程$\eqref{1} $的根：$i^2=(0,1)(0,1)=(-1,0)=-1$.任意复数$z=(x,y)=(x,0)+(0,1)(y,0)$现在可以用通常的方式写成

$$z=x+iy,\quad x,y\in \mathbb{R} \label{7} \tag{7} $$

这个写法十分接近域$P$元素的表达式$\eqref{5} $.注意到$\mathbb{Q} \subset \mathbb{R} \subset \mathbb{C} $.所以$\mathbb{C}$是一个特征为零的域（见第$4$章$\S 3$第$5$段）.

复数运算的几何解释

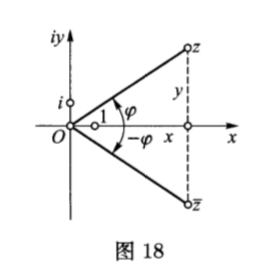
复平面$\mathbb{C}$的横轴通常叫作实轴，纵轴叫作虚轴，虚轴上的数$iy$叫作纯虚数，尽管“虚”这个词已经失去了它原有的含义.在写法$\eqref{7} $中，$x$叫作复数$z$的实部，记作$\mathrm{Re} z$，而$y$叫作$z$的虚部，记作$\mathrm{Im} z$.将任意复数$z=x+iy$对应到共轭复数$\overline{z} =x-iy$的映射叫作复共轭映射.在几何上，它对应于复平面沿实轴的反射（图$18$）.

一个值得注意的重要事实是

定理1$\quad $映射$z\mapsto \overline{z} $是域$\mathbb{C} $的$2$阶自同构，使得所有的实数保持不变.任意复数与它的共轭复数的和与积是实数.

证明$\quad $根据共轭复数的定义，若$x\in \mathbb{R} $，则$\overline{x} =x$.特别地，$\overline{0} =0,\overline{1} =1$.复共轭映射以$2$为阶的结论也是显然的：$\overline{\left( \overline{z} \right) } =z$.我们还需要验证关系式

$$\overline{z_1 +z_2 } =\overline{z}_1 +\overline{z}_2 ,\overline{z_1 z_2 } =\overline{z}_1 \overline{z}_2 ,\label{8} \tag{8} $$

它们可直接从公式$\eqref{6}$得到，只要把$\eqref{6}$式改写成下述形式即可：

$$\begin{align}
(x_1 +iy_1 )+(x_2 +iy_2 ) & =(x_1 +x_2 )+i(y_1 +y_2 ), \\
(x_1 +iy_1 )\cdot (x_2 +iy_2 ) & =(x_1 x_2 -y_1 y_2 )+i(x_1 y_2 +x_2 y_1 ).\\
\end{align} \label{9} \tag{9} $$

数$z=x+iy$与其共轭复数$\overline{z} =x-iy$的和与积是公式$\eqref{9} $的特殊情况：$z+\overline{z} =2x,z\overline{z} =x^2+y^2$.

注记$\quad $在复数域$\mathbb{C} $的诸多自同构中，复共轭是唯一的连续自同构（即将复平面$\mathbb{C} $上点的邻域仍变为邻域）.我们不给出这一论断的精确表述和证明.

复数$z=x+iy$的模是非负实数$\vert z\vert =\sqrt{z\overline{z} } =\sqrt{x^2+y^2} $.如所周知，点$z$在平面上的位置由它的极坐标完全确定：即从坐标原点到$z$点的距离$r=\vert z\vert $，以及横轴的正方向与坐标原点到$z$的正方向之间的夹角$\varphi $（见图$18$）.角$\varphi $叫作$z$的幅角，记作$\arg{z} =\varphi $.根据定义，$\arg{z} $可以取任意的正值和负值，但对于给定的$r$，相差$2\pi $的整倍数的辐角都对应于同一个数.数$0$的模是$\vert 0\vert =0$，但$0$的辐角没有定义.

对于复数而言，“大于”和“小于”关系没有意义，即它们之间不能用不等号连接：与实数不同，实数的辐角仅有两个主值，即$0$（正实数）和$\pi $（负实数），而复数不是有序的.

准确地说，在$\mathbb{C} $中不存在满足如下性质的$>$关系：

$\mathrm{i} )\;$如果$z\in \mathbb{C} $，则$z > 0,z=0$或$-z > 0$；

$\mathrm{ii} )\;$从$u > 0,v > 0$可得$u+v > 0$和$u\cdot v > 0$.

事实上，假设由$z\neq 0$可得$z^2 > 0$（如同在实数域$\mathbb{R} $中）.则有$1^2 > 0,i^2 > 0$，并根据$\mathrm{ii} )$，$0=i^2+1 > 0$，可得矛盾.

极坐标$r$和$\varphi $可以通过下述著名的公式确定$x$和$y$

$$x=r\cos{\varphi } ,y=r\sin{\varphi } ,z=r(\cos{\varphi } +i\sin{\varphi }) .\label{10} \tag{10} $$

它叫作复数$z$的三角形式.

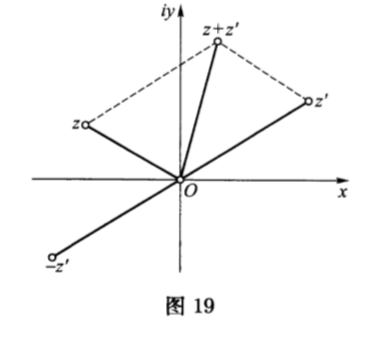
复数$z$和$z’$的和可以在笛卡儿坐标系中利用平行四边形法则简单地得到，或等价地说成，从坐标原点出发分别对应于数$z,z’$的有向线段（向量）相加的法则（见图$19$）.在图$19$中比较以点$0,z$和$z+z’$为顶点的三角形的三条边（它们等同于对应的复数的模），我们得到了重要的不等式.

$$\vert z+z’\vert \leqslant \vert z\vert +\vert z’\vert .\label{11} \tag{11} $$

我们指出，不等式$\eqref{11} $可以写成更一般的形式

$$\vert z\vert -\vert z’\vert \leqslant \vert z\pm z’\vert \leqslant \vert z\vert +\vert z’\vert ,$$

与实数域中相应的不等式完全类似.

复数的乘法可由极坐标方便地表示出来.

定理2$\quad $复数$z,z’$的乘积的模等于因子模的乘积，而辐角等于因子的辐角的和：

$$\vert zz’\vert =\vert z\vert \cdot \vert z’\vert ,\arg{zz’} =\arg{z} +\arg{z’} .\label{12} \tag{12} $$

类似地，

$$\left\vert \dfrac{z}{z’} \right\vert =\dfrac{\vert z\vert }{\vert z’\vert } ,\arg{\dfrac{z}{z’}} =\arg{z} -\arg{z’} .$$

证明$\quad $事实上，设$z$和$z’$的三角形式为

$$z=r(\cos{\varphi } +i\sin{\varphi }) ,z’=r’(\cos{\varphi’ } +i\sin{\varphi’} ).$$

直接相乘或利用$\eqref{9}$式得到

$$zz’=rr’[(\cos{\varphi } \cos{\varphi’} -\sin{\varphi} \sin{\varphi’ })+i(\cos{\varphi } \sin{\varphi’ }+\sin{\varphi } \cos{\varphi’ })] ,$$

根据众所周知的三角公式，这就是复数$zz’$的三角形式：

$$zz’=\vert z\vert \cdot \vert z’\vert [\cos{(\varphi +\varphi’ )}+i\sin{(\varphi +\varphi’ )}].$$

其次，若$z’’=z/z’$，则$z=z’z’’$.因而对乘积$z’z’’$应用已证明的公式$\eqref{12} $，我们就到得了关于分式$z/z’$的公式.

特别地，

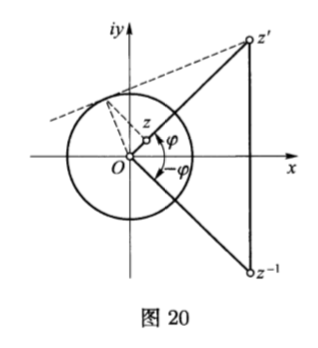
$$z^{-1} =\vert z\vert ^{-1} [\cos{(-\varphi )} +i\sin{(-\varphi )}] .$$

为了在复平面上得到$z^{-1}$（图$20$），需要对$z$做关于单位圆的反演，得到点$z’$（“反演”指$z’$到点$O$的距离是$z$到点$O$距离的倒数），然后做关于实轴的反射（或由$z’\mapsto \overline{z’} $给出的自同构），则$z’$的像即为$z^{-1} $.

事实上，关于积与和模的结论容易直接从定理$1$而不必通过几何直观推导出来.首先

$$\vert zz’\vert ^2 =zz’\overline{zz’} =zz’\overline{z} \overline{z’} =z\overline{z} z’\overline{z’} =\vert z\vert ^2 \vert z’\vert ^2 ,$$

故$\vert zz’\vert =\vert z\vert \cdot \vert z’\vert $.其次，注意到$\vert z\vert =\sqrt{x^2+y^2} \geqslant \sqrt{x^2} =\vert x\vert $，我们有

$$\begin{align}
\vert {1+z}\vert ^2 & =(1+z)(1+\overline{z} )=1+(z+\overline{z} )+z\overline{z} \\
& =1+2x+\vert z\vert ^2 \leqslant 1+2\vert z\vert +\vert z\vert ^2 =(1+\vert z\vert )^2 ,\\
\end{align}$$

从而$\vert 1+z\vert \leqslant 1+\vert z\vert $.现在若$z\neq 0$且$z’\neq 0$，则

$$\begin{align}
\vert z+z’\vert & =\vert z(1+z^{-1} z’)\vert =\vert z\vert \cdot \vert 1+z^{-1} z’\vert \\
& \leqslant \vert z\vert \left( 1+\vert z^{-1} z’\vert \right) =\vert z\vert \left(1+\vert z \vert ^{-1} \vert z’\vert \right)=\vert z\vert +\vert z’\vert .
\end{align}$$

从所得结果可以了解一个一般规律：表示复数的公式$\eqref{7}$用于加法的性质比较方便，而三角形式$\eqref{10} $便于得到乘法的性质.违背了这一规律就会导致特别复杂的计算，使事情变得模糊起来.

乘方和开方

将复数乘法公式$\eqref{12} $写成三角形式可推出棣莫弗公式

$$[r(\cos{\varphi} +i\sin{\varphi })]^n =r^n (\cos{n\varphi } +i\sin{n\varphi } ) \label{13} \tag{13} $$

对任意$n\in \mathbb{Z} $成立（另一种写法是$\vert z^n \vert =\vert z\vert ^n ,\arg{z^n} =n\cdot \arg{z} $）.运用公式$\eqref{13} $当$r=1$时的特殊情况，第$1$章$\S 7$的二项式$(1)$以及关系式

$$i^2=-1,i^3=-i,i^4=1,i^{4k+l} =i^l$$

可以得到倍角的正弦和余弦

$$\begin{align}
\cos{n\varphi } & =\sum_{k\geqslant 0} (-1)^k {n \choose 2k} \cos{}^{n-2k} \varphi \cdot \sin{}^{2k} \varphi ,\\
\sin{n\varphi } & =\sum_{k\geqslant 0} (-1)^k {n \choose {2k+1} } \cos{}^{n-1-2k} \varphi \cdot \sin{}^{2k+1} \varphi .
\end{align} \label{14} \tag{14} $$

公式$\eqref{14} $当$n=2$时的特殊情况我们早已在证明定理$2$的过程中使用过了.

注记$\quad $设$e^{\alpha } =\displaystyle \lim_{n\to \infty } (1+\alpha /n)^n$.在数学分析中用复函数的幂级数展开证明过欧拉公式

$$e^{i\varphi } =\cos{\varphi } +i\sin{\varphi } \label{15} \tag{15} $$

注意到

$$e^{i\varphi } e^{i\varphi’ } =e^{i(\varphi +\varphi’ )} ,(e^{i\varphi })^n =e^{in\varphi } .$$

利用欧拉公式可以得到上述所有的结果.复数$z$的三角形式也可以写成

$$z=\vert z\vert e^{i\varphi } .$$

下面我们来讨论怎样求一个复数的任意次方根，一个基本的问题是，这样的方根是否永远存在？答案是肯定的，棣莫弗公式对这一问题从本质上给出了完全的解答.设给定复数$z=r(\cos{\varphi } +i\sin{varphi })$，我们希望找到一个复数$z’=r’(\cos{\varphi’ } +i\sin{\varphi’ }) $，使得$(z’)^n =z$.对$(z’)^n $使用棣莫弗公式，并比较等式$(z’)^n =z$两端的模和辐角，我们有$(r’)^n =r$和$n\varphi’ =\varphi +2\pi k$（我们在这里加上一项$2\pi k$，是因为辐角只精确到相差$2\pi $的整倍数）.于是

$$r’=\sqrt[n]{r} ,\varphi’ =\dfrac{\varphi +2\pi k}{n} $$

（$\sqrt[n]{r} $指正实数的$n$次算术根）.于是，根$\sqrt[n]{z} $是存在的，但并不唯一确定.当$k=0,1,\cdots ,n-1$时，$z’$取$n$个不同的值，它们穷尽了所有可能的根，记$k=nq+r,0\leqslant r\leqslant n-1$，则有

$$\varphi’ =\dfrac{\varphi +2\pi r}{n} +2\pi q.$$

我们证明了

定理3$\quad $任意复数$z=\vert z\vert (\cos{\varphi } +i\sin{\varphi } )$开$n$次方总是可能的.$z$的全部$n$个$n$次方根健分布在以原点为圆心，$\sqrt[n]{\vert z\vert } $为半径的圆的内接正$n$边形的顶点上：

$$\sqrt[n]{z} =\sqrt[n]{\vert z\vert } \left( \cos{\dfrac{\varphi +2\pi k}{n} } +i\sin{\dfrac{\varphi +2\pi k}{n} } \right) ,\label{16} \tag{16} $$

$k=0,1,\cdots ,n-1$.

推论$\quad 1$的$n$次方根（单位根）由公式

$$\sqrt[n]{1} =\varepsilon_k =\cos{\dfrac{2\pi k}{n} } +i\sin{\dfrac{2\pi k}{n} } \label{17} \tag{17} $$

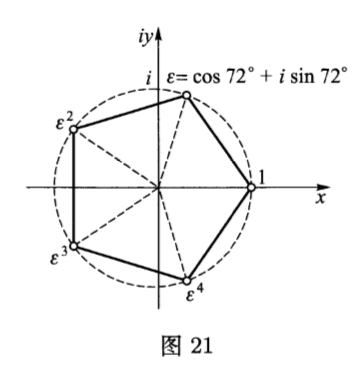
给出，$k=0,1,\cdots ,n-1$.它们分布在以原点为圆心，$1$为半径的圆的内接正$n$边形的顶点上.

从公式$\eqref{16} $和$\eqref{17} $立即可见，形如$\sqrt[n]{z} $的实根为零个，$1$个或$2$个，而形如$\sqrt[n]{1}$的实根有$1$个或$2$个（图$21$给出了$1$的$5$次方根）.

$1$的一个$n$次方根称为本原的（或原的），如果它不是$1$的更低次数的方根.例如

$$\varepsilon =\varepsilon_1 =\cos{\dfrac{2\pi }{n}} +i\sin{\dfrac{2\pi }{n} } ,\varepsilon_{n-1} $$

是$1$的$n$次本原根.

任意其他的根$\varepsilon_k $是本原根的方幂

$$\varepsilon_k =\varepsilon_1^k ,$$

这仍然可以从棣莫弗公式看出来.进一步$\varepsilon_k \varepsilon_l =\varepsilon_{k+l} $，其中$k+l$是取模$n$得到的最小非负整数.特别地，$\varepsilon_k^{-1} =\varepsilon_{n-k} ,\varepsilon_0 =1$.在学习过群论之后，我们注意到，$1$的$n$次方根构成了一个$n$阶循环群$\langle \varepsilon \rangle $.

这样就得到了$n$阶循环群的又一个模型.对于每一个因子$d\vert n$，$\langle \varepsilon \rangle $中恰有一个$d$阶子群$\langle \varepsilon^{n/d} \rangle $.根$\varepsilon_m $是本原的，当且仅当$\langle \varepsilon_m \rangle =\langle \varepsilon \rangle $，当且仅当$\mathrm{Card} \langle \varepsilon^m \rangle =n$，当且仅当$m$与$n$互素.例如当$n=12$时，$12$次本原根有$\varepsilon ,\varepsilon ^5 ,\varepsilon ^7 ,\varepsilon ^{11} $.当$n=p$是素数的情况下，所有的异于$1$的根都是本原的.从代数的观点来看，不计几何位置，所有的$n$次本原根都是等价的.

回到对任意复数$z\neq 0$开$n$次方的问题上来，我们指出，如果$z’$是某个取定的根（例如$z’=\sqrt[n]{\vert z\vert } (\cos{\dfrac{\varphi }{n} } +i\sin{\dfrac{\varphi }{n} })$），则所有其他的根形如$z’\varepsilon_k ,k=0,1,\cdots ,n-1$.这一结论与公式$\eqref{16}$是一致的.

唯一性定理

复数域$\mathbb{C} $比之于实数域$\mathbb{R} $的优越性我们可以稍后再作充分的评价，但已有的一个事实，$\mathbb{C} $包含有$1$的任意次方根就足以提高人们对复数域的兴趣.我们指出，$\mathbb{C} $是$\mathbb{R} $上的$2$维向量空间（在第$2$章$\S 1$第$2$段定义的意义下），基元素可取$1,i\colon \mathbb{C} =\langle 1,i\rangle_{\mathbb{R} } $.

一个自然的问题是，具有类似性质的域还有多少？我们有下述唯一性定理.

定理4$\quad \mathbb{R} $上的任意一个$2$维向量空间$K$，如果还是一个结合，交换，具有单位元且无零因子的环，则必同构于域$\mathbb{C} $.

证明$\quad $不失一般性，将$1\cdot \mathbb{R} $与$\mathbb{R} $等同，并认为$\mathbb{R} $包含在$K$中.因为$\underset{\mathbb{R}}{\mathrm{dim} } K=2$，故存在元素$e\in K\setminus \mathbb{R} $，使得$1$和$e$构成向量空间$K$在$\mathbb{R} $上的一个基.设$e^2=\alpha \cdot 1+2\beta \cdot e$，其中$\alpha ,\beta \in \mathbb{R} $，对于元素$f=e-\beta \notin \mathbb{R} $，有$f^2 =\gamma $，此处$\gamma =\alpha +\beta ^2 \in \mathbb{R} $.显然$\gamma < 0$，否则$\sqrt{\gamma } \in \mathbb{R} $，而$f=\pm \sqrt{\gamma } \in \mathbb{R} $与$f\notin \mathbb{R} $矛盾.这样存在$\delta \in \mathbb{R} $，满足$\delta ^2 =-\gamma ^{-1} $.令$j=\delta f$，有$j^2=-1$，且容易验证（如同对$\mathbb{C} $的作法），$K$中的每个非零元可逆，即$K$是域.映射$\varphi \colon \mathbb{C} \to K,x+iy \mapsto x+jy$即为所求的域的同构.

在这一证明中，我们何处用到了$K$是无零因子环这一条件？首先，若没有这个条件，有可能发生$e^2=0$，从而$\alpha =\beta =0,\gamma =0$的情况.其次，我们断定由$\gamma \geqslant 0$可得$f=\pm \sqrt{\gamma } $.而这事实上是因为$0=f^2 -\gamma =(f-\sqrt{\gamma } )(f+\sqrt{\gamma } )\Rightarrow f-\sqrt{\gamma } =0$或$f+\sqrt{\gamma } =0$.

除了$\mathbb{Q} $与$\mathbb{R} $，域$\mathbb{C} $还包含有许多其他的子域.其中特别有趣的是将某个不包含在$\mathbb{Q} $中的$\mathbb{C} $的元素添加到$\mathbb{Q} $上，所得到的域$\mathbb{Q} $的扩张.

例1（二次域）$\quad $设$d$是一个非零整数，可能是负数，使得$\sqrt{d} \notin \mathbb{Q} $.域$\mathbb{Q} (\sqrt{d} )\subset \mathbb{C} $当$d > 0$时叫作实二次域，当$d < 0$时叫作虚二次域.我们曾在第$4$章$\S 3$中讨论过域$\mathbb{Q} (\sqrt{2} )$.在定理$4$中将$j$换成$\sqrt{d} $，关系式$j^2=-1$换成$(\sqrt{d} )^2=d$，重复它的证明过程得到

$$\mathbb{Q} (\sqrt{d} )=\left\lbrace a+b\sqrt{d} \vert a,b\in Q\right\rbrace .$$

特别地，

$$\begin{align}
(a_1 +b_1 \sqrt{d} ) +(a_2 +b_2 \sqrt{d} ) & =(a_1 +a_2 )+(b_1 +b_2 )\sqrt{d} ,\\
(a_1 +b_1 \sqrt{d} )(a_2 +b_2 \sqrt{d} ) & =(a_1 a_2 +b_1 b_2 d)+(a_1 b_2 +a_2 b_1 )\sqrt{d} .
\end{align} \label{18} \tag{18} $$

其次，若$a+b\sqrt{d} \neq 0$（即$a,b$不同时为零），

$$(a+b\sqrt{d} )^{-1} =\dfrac{a}{a^2-db^2} +\dfrac{b}{a^2-db^2} \sqrt{d} $$

运用公式$\eqref{18} $易验证，映射

$$f\colon a+b\sqrt{d} \mapsto a-b\sqrt{d} $$

是域$\mathbb{Q} (\sqrt{d} )$的自同构，（类似于复共轭映射）.

一个数$\alpha =a+b\sqrt{d} $的范数定义为

$$N(\alpha )=a^2-db^2=\alpha f(\alpha ).$$

显然，$N(\alpha )=0\Leftrightarrow \alpha =0$.其次，因为$f$是自同构，

$$N(\alpha \beta )=\alpha \beta f(\alpha \beta )=\alpha \beta f(\alpha )f(\beta )=\alpha f(\alpha )\cdot \beta f(\beta ) =N(\alpha )\cdot N(\beta ).$$

特别地，$N(\alpha )\cdot N(\alpha ^{-1}) =N(\alpha \alpha ^{-1})=N(1)=1$.因而范数具备复数域$\mathbb{C}$中模平方的主要性质.

复数的初等几何

实向量空间$\mathbb{C} =\langle 1,i\rangle_{\mathbb{R} } $是欧氏空间：它被赋予了一个正定的数量积

$$(z_1 \vert z_2 )=\mathrm{Re} z_1 \overline{z_2 } =x_1 x_2 +y_1 y_2 ,$$

其中$z_k =x_k +iy_k ,k=1,2$.柯西-布尼亚柯夫斯基-施瓦兹不等式成立

$$\vert (z_1 \vert z_2 )\vert \leqslant \vert z_1 \vert \cdot \vert z_2 \vert ,$$

这是因为$\vert (z_1 \vert z_2 )\vert =\vert \mathrm{Re} z_1 \overline{z_2 } \leqslant \vert z_1 \overline{z_2 } \vert =\vert z_1 \vert \vert \overline{z_2 } \vert =\vert z_1 \vert \vert z_2 \vert .$

两个向量（复数）$z_1 ,z_2 $叫作正交的，或垂直的，若$(z_1 \vert z_2 )=0$.

从关系式$\eqref{12} $不难推出，两个向量$z,cz\in \mathbb{C} ^{\ast } $是正交的，当且仅当$c$是纯虚数.

过点$u,v\in \mathbb{C} $的直线由参数方程

$$w=u+(v-u)t,t\in \mathbb{R} ,$$

给出.

设$u=x_1 +iy_1 ,v=x_2 +iy_2 $，则通过两点$(x_1 ,y_1 )$与$(x_2 ,y_2 )$的直线方程为$\dfrac{y-y_1 }{y_2 -y_1 } =\dfrac{x-x_1 }{x_2 -x_1 } $，参数方程为$\begin{cases} x=x_1 +(x_2 -x_1 )t \\ y=y_1 +(y_2 -y_1 )t \end{cases} $ $(-\infty < t < +\infty )$，由参数式得复数形式参数方程为$w=u+(v-u)t,(-\infty < t < +\infty )$，所以连接$u=x_1 +iy_1 $与$v=x_2 +iy_2 $的直线段的参数方程为：$w=u+(v-u)t ,t\in \mathbb{R} $.

于是两条直线$w=u+(v-u)t$与$w’=u’+(v’-u’)t$的正交性可由关系式$(v-u\vert v’-u’)=0$得到.三个点$z_1 ,z_2 ,z_3 \in \mathbb{C} ,z_1 \neq z_2 $，位于同一直线上，当且仅当

$$\dfrac{z_3 -z_2 }{z_2 -z_1 } \in \mathbb{R} ,\label{19} \tag{19} $$

即

$$z_3 \overline{z}_2 -z_3 \overline{z}_1 -z_1 \overline{z}_2 \in \mathbb{R} .$$

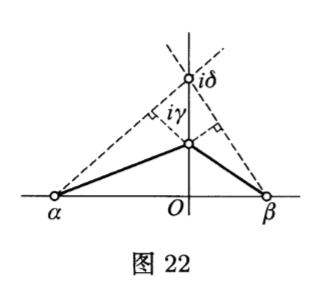
对直线的正交性作少许讨论.给出任意一个三角形，为此给定实轴上的两向量$\alpha ,\beta $，而第三个向量$i\gamma $在虚轴上，易验证三角形的三条高交于一点$i\delta $，其中$\delta =-\alpha \beta /\gamma $.例如验证$(-\alpha +i\delta \vert -\beta +i\gamma )=0$（图$22$）.

四个点$z_1 ,z_2 ,z_3 ,z_4 \in \mathbb{C} ,z_1 \neq z_4 ,z_2 \neq z_3 $的交比$[z_1 ,z_2 ,z_3 ,z_4 ]$的概念在许多几何问题中发挥了重要作用.（细节见$[BAII]$）.根据定义

$$\begin{align} [z_1 ,z_2 ,z_3 ,z_4 ] & =\dfrac{z_1 -z_2 }{z_1 -z_4 } \colon \dfrac{z_3 -z_2 }{z_3 -z_4 } \\ & =\dfrac{(z_1 -z_2 )(z_3 -z_4 )}{(z_1 -z_4 )(z_3 -z_2 )} =\dfrac{(z_1 -z_2 )(z_3 -z_4 )(\overline{z}_1 -\overline{z}_4 )(\overline{z}_3 -\overline{z}_2 )}{\vert z_1 -z_4 \vert ^2 \cdot \vert z_3 -z_2 \vert ^2} \label{20} \tag{20} \end{align} $$

是一个复数，依赖于数列$z_1 ,z_2 ,z_3 ,z_4 $的排列顺序.在循环置换下有

$$[z_1 ,z_2 ,z_3 ,z_4 ]=[z_1 ,z_2 ,z_3 ,z_4 ]^{-1} .$$

我们指出，关系式$\eqref{20} $定义的交比在位移$T_a \colon z\mapsto z+a $下保持不变.而三点$z_1 ,z_2 ,z_3 $不共线这一性质也在位移下不变.因而（当计算$[z_1 ,z_2 ,z_3 ,z_4 ]$时），以$z_1 ,z_2 ,z_3 $为顶点的三角形的外接圆的圆心可以放在坐标原点上.但当$\vert z_1 \vert =\vert z_2 \vert =\vert z_3 \vert $时，易验

$$(z_1 -z_2 )(z_3 -z_4 )(\overline{z}_1 -\overline{z}_4 )(\overline{z}_3 -\overline{z}_2 )-i(\vert z_3 \vert ^2 -\vert z_4 \vert ^2) \cdot \mathrm{Im} (z_3 \overline{z}_2 -z_3 \overline{z}_1 -z_1 \overline{z}_2 ) \in \mathbb{R} $$

（建议读者在本节后面的习题中完成这一验证）.根据$\eqref{19} $式，$\mathrm{Im} (z_3 \overline{z}_2 -z_3 \overline{z}_1 -z_1 \overline{z}_2 ) \neq 0$，而在这种情况下，乘积$(z_1 -z_2 )(z_3 -z_4 )(\overline{z}_1 -\overline{z}_4 )(\overline{z}_3 -\overline{z}_2 ) $是实数，或等价地说（见$\eqref{20}$），$[z_1 ,z_2 ,z_3 ,z_4 ]$是实数，当且仅当$\vert z_3 \vert ^2 -\vert z_4 \vert ^2 =0$，即$\vert z_3 \vert =\vert z_4 \vert $.这意味着$z_k ,1\leqslant k\leqslant 4$，是模相等的四个复数，位于同一个圆周上.

该论断当四个点中的某三个点不共线时成立.我们指出，交比$[z_1 ,z_2 ,z_3 ,z_4 ]$是实数的性质在序列$z_1 ,z_2 ,z_3 ,z_4 $的循环置换下保持不变.我们证明了下述论断.

定理5$\quad $设不在同一直线上的四个点$z_1 ,z_2 ,z_3 ,z_4 \in \mathbb{C} ,z_1 \neq z_4 ,z_2 \neq z_3 $，这四点共圆，当且仅当它们的交比是实数.

这仅仅是用交比的语言得到的诸多几何性质中的一例.

作为本段的结束，我们用几何手段来构造在数学史上占据显著地位的一些新的数域.

例（可构作性数域）$\quad $在笛卡儿平面上给定两点$(0,0)$和$(1,0)$.后面所有的结构仅在圆规和直尺的帮助下实现.如果构作了点$P$和$Q$，我们自然可以认为连接它们的$PQ$也构作出来了.如果构作了点$P$和线段$r$，那么以$P$为圆心，$r$为半径的圆周也可以作出来.已构作出的两条直线（线段）的交点或两个圆的交点的构作也是在这种意义之下.

复数$a+bi$称为可构作的，如果从点$(0,0)$和$(1,0)$出发，经过有限次上述的（允许）构作，我们可以作出点$P=(a,b)$.不难看出，$a+bi$的可构作性，等价于$\vert a\vert $和$\vert b\vert $的可构作性.平面上可在圆规直尺的帮助下构作出来的点的集合，也就是说所有的可构作复数的集合记作$CS$.

定理6$\quad $集合$CS$是域$\mathbb{C} $的子域.

证明$\quad $从数的可构作性定义直接得到，$CS$关于加法运算是封闭的（点$z+z’$是圆心在点$z’$，半径为$\vert z\vert $与圆心在点$z$，半径为$\vert z’\vert $的两个圆的交），而如果$z=x+iy\in CS$可得$-z=-x-iy\in CS$.

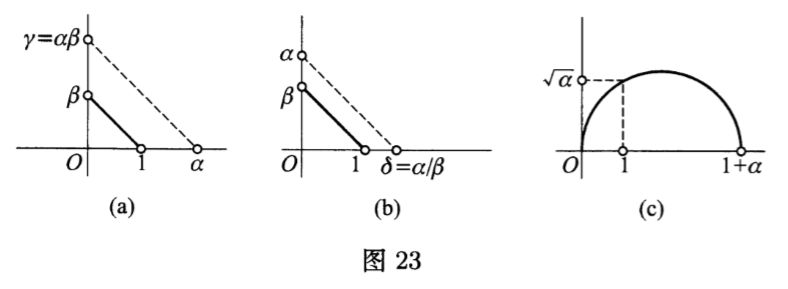
将长度可构作的线段$1,\alpha ,\beta $置于坐标轴上，我们来考察图$23,(a)$和$(b)$中的相似三角形（虚线代表新的可构作线段），就得到了积$\gamma =\alpha \beta $和商$\delta =\alpha /\beta $的可构作性.因为

$$\begin{align} zz’ & =(x+iy)(x’+iy’)=(xx’-yy’)+i(xy’+x’y), \\ \dfrac{1}{z} & =\dfrac{x}{x^2+y^2} -i\dfrac{y}{x^2+y^2} \end{align} $$

积$zz’$和商$\dfrac{1}{z}$的可构作性归结为$\gamma $和$\delta $型线段的可构作性.因而我们证明了集合$CS$关于复数域$\mathbb{C}$的所有的运算都是封闭的.

注记$\quad 1)\;CS$在复共轭映射$z\mapsto \overline{z} $下不变.

$2)\;$图$23(c)$表明，可构作实数$\alpha > 0$的二次方根$\sqrt{\alpha }$是可构作的.这件事对于任意可构作复数$z$亦成立.

$CS$的任意子域$F\subset CS$通常称为可构作数域.显然，$\mathbb{Q} \subset CS$，且任意可构作数域是特征为零的域.根据注记$2)$，所有的二次域（见$\S 5$的例）是可构作的.