与数$e$有关的习题

$69$.证明：数列

$$x_n =\left( 1+\dfrac{1}{n} \right) ^n \quad (n=1,2,\cdots )$$

是单调增的，且上方有界，而数列

$$y_n =\left( 1+\dfrac{1}{n} \right) ^{n+1} \quad (n=1,2,\cdots )$$

是单调减的，且下方有界.由此推出这些数列有共同的极限：

$$\lim_{n\to \infty } \left( 1+\dfrac{1}{n} \right) ^n =\lim_{n\to \infty } \left( 1+\dfrac{1}{n} \right) ^{n+1} =e.$$

提示：先作出比$\dfrac{x_{n+1}}{x_n} ,\dfrac{y_n}{y_{n-1}} $，并利用习题$7$的不等式.

证$1$（用习题$7$的伯努利不等式）当$n\geqslant 2$时对数列$\lbrace x_n \rbrace $的后项与前项之比可以估计如下：

$$\begin{align}
\dfrac{x_n}{x_{n-1}} & =\left( \dfrac{n+1}{n} \right) ^n \cdot \left( \dfrac{n-1}{n} \right) ^{n-1} =\dfrac{n}{n-1} \cdot \left( \dfrac{n^2-1}{n^2} \right) ^n \\
& =\dfrac{n}{n-1} \cdot \left( 1-\dfrac{1}{n^2} \right) ^n > \dfrac{n}{n-1} \cdot \left( 1-\dfrac{1}{n} \right) =1,
\end{align}$$

其中利用了习题$7$的伯努利不等式，并从该题中等号成立的条件可知这时一定成立严格的不等号.于是知道数列$\lbrace x_n \rbrace $严格单调递增.

对于$\lbrace y_n \rbrace $类似地有

$$\begin{align}
\dfrac{y_n}{y_{n-1}} & =\left( \dfrac{n+1}{n} \right) ^{n+1} \cdot \left( \dfrac{n-1}{n} \right) ^n =\dfrac{n+1}{n} \cdot \dfrac{1}{\left( 1+\dfrac{1}{n^2-1} \right) ^n } \\
& < \dfrac{n+1}{n} \cdot \dfrac{1}{1+\dfrac{n}{n^2-1} } < \dfrac{n+1}{n} \cdot \dfrac{1}{1+\dfrac{1}{n} } =1,
\end{align}$$

可知$\lbrace y_n \rbrace $严格单调递减.又因对每一个$n$有$x_n < y_n $，因此任一确定的$y_n $，例如$y_1 =4$，都是$\lbrace x_n \rbrace $的上界.同理，任一确定的$x_n $，例如$x_1 =2$，都是$\lbrace y_n \rbrace $的下界，故两个极限$\displaystyle \lim_{n\to \infty } x_n ,\lim_{n\to \infty } y_n $都存在.最后由$y_n =x_n (1+\dfrac{1}{n} )$得知$\displaystyle \lim_{n\to \infty } y_n =\lim_{n\to \infty } x_n $，记其为$e$，即得所证.

证$2$（用平均值不等式）将$x_n $“无中生有”地看成为不全相等的$n+1$个非负数的乘积，就可以从平均值不等式$G < A$推出数列$\lbrace x_n \rbrace $严格单调递增：

$$x_n =1\cdot \left( \dfrac{n+1}{n} \right) ^n < \left( \dfrac{1+n\left( \dfrac{n+1}{n} \right) }{n+1} \right) ^{n+1} =\left( \dfrac{n+2}{n+1} \right) ^{n+1} =x_{n+1} .$$

然后同样地将$y_n $看成为$n+2$个不全相等的正数的乘积，就可用平均值不等式$G > H$推出数列$\lbrace y_n \rbrace $严格单调递减：

$$y_n =1\cdot \left( \dfrac{n+1}{n} \right) ^{n+1} > \left( \dfrac{n+2}{1+(n+1)\left( \dfrac{n}{n+1} \right) } \right) ^{n+2} =\left( \dfrac{n+2}{n+1} \right) ^{n+2} =y_{n+1} .$$

以下同证$1$.

注$\quad $为了定义数$e$，只需要用上述两数列中的任何一个就够了.这时不难分别证明两个数列有界.例如用平均值不等式$G < A$可以得到

$$x_n \cdot \dfrac12 \cdot \dfrac12 < \left( \dfrac{n\left( \dfrac{n+1}{n} \right) +\dfrac12 +\dfrac12 }{n+2} \right) ^{n+2} =1,$$

可见$\lbrace x_n \rbrace $以$4$为其上界.再用平均值不等式$G > H$可以得到

$$y_n \cdot \dfrac12 =\left( \dfrac{n+1}{n} \right) ^{n+1} \cdot \dfrac12 > \left( \dfrac{n+2}{2+(n+1)\left( \dfrac{n}{n+1} \right) } \right) ^{n+2} =1,$$

可见$\lbrace y_n \rbrace $有下界$2$.在习题$69$中同时讨论两个数列，这样做的好处是为许多问题的讨论提供了更多的工具，这在下面的许多习题中有用.

$70$.证明：

$$0 < e-\left( 1+\dfrac{1}{n} \right)^n < \dfrac{3}{n} \quad (n=1,2,\cdots ).$$

当指数$n$取什么样的数值时，表达式$\left( 1+\dfrac{1}{n} \right) ^n $与数$e$相差不到$0.001$？

证：引用上题的记号和结论，则就对每个正整数$n$有$x_n < e < y_n $，因此有

$$0 < e-x_n < y_n -x_n =\left( 1+\dfrac{1}{n} \right)^n \cdot \dfrac{1}{n} .$$

又取$y_5 =\left( 1+\dfrac15 \right) ^6 \approx 2.986 < 3$为数列$\lbrace x_n \rbrace $的上界，则就得到所要的不等式.

从所得的不等式即可知道当$n > 3000$时$\left( 1+\dfrac{1}{n} \right) ^n $与数$e$的差小于$0.001$.

$71$.设$p_n (n=1,2,\cdots )$为趋于$+\infty $的任意数列，而$q_n (n=1,2,\cdots )$为趋于$-\infty $的任意数列（$p_n ,q_n \notin [-1,0]$）.求证：

$$\lim_{n\to \infty } \left( 1+\dfrac{1}{p_n } \right) ^{p_n } =\lim_{n\to \infty } \left( 1+\dfrac{1}{q_n } \right) ^{q_n } =e.$$

证：条件$p_n ,q_n \notin [-1,0] $等价于$1+\dfrac{1}{p_n }$和$1+\dfrac{1}{q_n}$都大于$0$.

$(1)$不妨先对于每一个$p_n $都是正整数的情况作出证明，然后推广到一般情况.

这时对$\varepsilon > 0$，存在$N$，使得当$n > N$时成立$0 < e-\left( 1+\dfrac{1}{n} \right) ^n < \varepsilon $.又由于$p_n \to +\infty $,对上述$N$，存在$N_1 $，使得当$n > N_1 $时成立$p_n > N$.

综合以上，由于$p_n $为正整数，因此当$n > N_1 $时就有$0 < e-\left( 1+\dfrac{1}{p_n } \right) ^{p_n } < \varepsilon $.这就证明了$\displaystyle \lim_{n\to \infty } \left( 1+\dfrac{1}{p_n } \right) ^{p_n } =e.$

对一般情况，对$p_n $取整数部分得到$[p_n ]\leqslant p_n < [p_n ]+1$.于是有不等式

$$\left( 1+\dfrac{1}{[p_n ]+1} \right) ^{[p_n ]} \leqslant \left( 1+\dfrac{1}{p_n } \right) ^{p_n } \leqslant \left( 1+\dfrac{1}{[p_n ]} \right) ^{[p_n ]+1} .$$

由于这时也有$[p_n ] \to +\infty $，于是从上述夹逼关系和两边都趋于$e$就知道中间的数列也收敛于$e$.

$(2)$对于$q_n \to -\infty $的情况可以将问题归结为$(1)$来解决.这只要如下变换即可：

$$\begin{align}
\left( 1+\dfrac{1}{q_n } \right) ^{q_n } & =\left( \dfrac{q_n }{1+q_n } \right) ^{-q_n } =\left( 1+\dfrac{1}{-q_n -1} \right) ^{-q_n } \\
& =\left( 1+\dfrac{1}{-q_n -1} \right) ^{-q_n -1} \cdot \left( \dfrac{q_n }{1+q_n } \right) .
\end{align}$$

注$\quad $习题$71$是很强的结论，它包含了许多特殊情况为其特例，且可在今后的函数极限中通过归结原理过渡到更一般的结论.

$72$.已知

$$\lim_{n\to \infty } \left( 1+\dfrac{1}{n} \right) ^n =e,$$

求证：

$$\lim_{n\to \infty } \left( 1+1+\dfrac{1}{2!} +\dfrac{1}{3!} +\cdots +\dfrac{1}{n!} \right) =e.$$

由此推出公式

$$e=1+1+\dfrac{1}{2!} +\dfrac{1}{3!} +\cdots +\dfrac{1}{n!} +\dfrac{\theta_n }{n!n} ,$$

其中$0 < \theta_n < 1$，并计算数$e$，精确到$10^{-5}$.

证：记$z_n =1+1+\dfrac{1}{2!} +\dfrac{1}{3!} +\cdots +\dfrac{1}{n!} $.从该式联想到将习题$69$中的第一个数列的通项$x_n =\left( 1+\dfrac{1}{n} \right) ^n $作二项式展开，即有

$$x_n =1+1+\dfrac{1}{2!} ( 1-\dfrac{1}{n} ) +\cdots +\dfrac{1}{k!} (1-\dfrac{1}{n} ) \cdots (1-\dfrac{k-1}{n} ) +\cdots +\dfrac{1}{n!} (1-\dfrac{1}{n} )\cdots (1-\dfrac{n-1}{n} ).$$

比较待求极限的数列$z_n $与已知极限为$e$的数列$x_n $，可见它们之间的差别在于后者的展开式中从第三项起每一项多乘了一些介于$0,1$之间的因子.由于其中有阶乘的倒数，故两者相差不大，有望$z_n -x_n \to 0(n\to \infty )$.

为了估计$z_n -x_n $，注意到$x_n $中的$(1-\dfrac{1}{n} )(1-\dfrac{2}{n} )\cdots (1-\dfrac{k-1}{n} )$等等可用习题$6$中的伯努利不等式分离出$1$，并得较好的估计.

先用该不等式估计$z_n $与$x_n $的和式中的对应项$(k\geqslant )$的差：

当$k=2$时下面出现的$(k-2)!$为$0!$.在数学中约定$0!=1$.

$$\begin{align}
0 & \leqslant \dfrac{1}{k!} -\dfrac{1}{k!} (1-\dfrac{1}{n} )(1-\dfrac{2}{n} )\cdots (1-\dfrac{k-1}{n} ) \\
& \leqslant \dfrac{1}{k!} \left( 1-(1-\dfrac{(k-1)k}{2n} )\right) =\dfrac{1}{(k-2)!} \cdot \dfrac{1}{2n} .
\end{align}$$

将上式对$k$从$2$到$n$求和$(n\geqslant 3)$得到

$$\begin{align}
0\leqslant z_n -x_n & \leqslant \dfrac{1}{2n} \left( 1+1+\dfrac{1}{2!} +\dfrac{1}{3!} +\cdots +\dfrac{1}{(n-2)!} \right) \\
& \leqslant \dfrac{1}{2n} \left( 1+1+\dfrac12 +\dfrac{1}{2^2} +\cdots +\dfrac{1}{2^{n-3}} \right) < \dfrac{3}{2n} \to 0.
\end{align}$$

从$x_n \leqslant z_n < x_n +\dfrac{3}{2n} $出发，用夹逼定理即可得到

$$\lim_{n\to \infty } (1+1+\dfrac{1}{2!} +\dfrac{1}{3!} +\cdots +\dfrac{1}{n!} ) =e.$$

下面估计用$z_n $近似$e$的误差.不妨设$m > n$，得

$$\begin{align}
0 < z_m -z_n & =\dfrac{1}{(n+1)!} +\cdots +\dfrac{1}{m!} \\
& < \dfrac{1}{(n+1)!} \left( 1+\dfrac{1}{n+2} +\dfrac{1}{(n+2)^2} +\cdots +\dfrac{1}{(n+2)^{m-n-1} }\right) \\
& < \dfrac{1}{(n+1)!} \cdot \dfrac{1}{1-\dfrac{1}{n+2}} =\dfrac{1}{(n+1)!} \cdot \dfrac{n+2}{n+1} .
\end{align}$$

固定$n$，令$m\to \infty $，就得到

$$0\leqslant e-z_n \leqslant \dfrac{n+2}{n!(n+1)^2} < \dfrac{1}{n!n} .$$

注意$\lbrace z_n \rbrace $严格单调递增趋于$e$，故上式左端的$\leqslant $号中等号恒不成立，即有

$$0 < e-z_n < \dfrac{1}{n!n} .\label{1} \tag{1} $$

由此可见存在$\theta_n \in (0,1)$，使得

$$e=1+1+\dfrac{1}{2!} +\cdots +\dfrac{1}{n!} +\dfrac{\theta_n }{n!n} .$$

最后按照误差$10^{-5}$的要求来计算$e$的近似值.根据误差限不超过$\dfrac{1}{n!n}$，经尝试知道取$n=8$时误差不超过$\dfrac{3}{10^6}$.然后如右面的附表所示将每一项计算到第$6$位小数，并在其后用$\pm $号标出四舍或五入的情况，每一步所引起的误差不会超过$0.5/10^6$.

$$\begin{array}{ccc} & 2.000\;000 & \\ \dfrac{1}{2!} = & 0.500\;000 & \\ \dfrac{1}{3!} = & 0.166\;667 & - \\ \dfrac{1}{4!} = & 0.041\;667 & - \\ \dfrac{1}{5!} = & 0.008\;333 & + \\ \dfrac{1}{6!} = & 0.001\;389 & - \\ \dfrac{1}{7!} = & 0.000\;198 & + \\ \dfrac{1}{8!} = & 0.000\;025 & - \\ \hline & 2.718\;279 & \end{array}$$

与右边附表最后计算的结果$2.718\;279$比较，除了因为取$n=8$而舍去的（至多）$3\cdot 10^{-6}$之外，还因两次“四舍”而产生（至多）$1\cdot 10^{-6}$的误差，因此数$e$可能比$2.718\;279$大（确实如此），但不会超过$4\cdot 10^{-6}$以上.

同理因为四次“五入”而产生（至多）$2\cdot 10^{-6}$的误差，因此$e$也可能比$2.718\;279$小，但不会减少$2\cdot 10^{-6}$以上.这样就知道数$e$一定满足以下不等式：

$$2.718\;277 < e < 2.718\;283.$$

可见取$e\approx 2.718\;28$就可保证误差小于$10^{-5}$.

$73$.证明：数$e$是无理数.

证：用反证法.设$e=\dfrac{p}{q}$，其中$p,q$是正整数.

由于$\eqref{1}$对每个正整数$n$都成立，因此可以取$n=q$得到不等式

$$0 < \dfrac{p}{q} -\left( 2+\dfrac{1}{2!} +\cdots +\dfrac{1}{q!} \right) < \dfrac{1}{q!q} .$$

乘以$q!q$后左边为$0$，右边为$1$，而中间却是一个整数，这是不可能的.

$74$.证明不等式：

$$\left( \dfrac{n}{e} \right) ^n < n! < e\left( \dfrac{n}{2} \right) ^n .$$

证$1$：$(1)$对左边的不等式用数学归纳法.$n=1$时是平凡的.设$n=k$是该不等式成立，则当$n=k+1$时就有

$$\left( \dfrac{k+1}{e} \right) ^{k+1} =\left( \dfrac{k}{e} \right) ^k \cdot \left( 1+\dfrac{1}{k} \right) ^k \cdot \dfrac{k+1}{e} < (k+1)! ,$$

其中利用了$\left( \dfrac{k}{e} \right) ^k < k!$的归纳假设和对每一个$k$有$\left( 1+\dfrac{1}{k} \right) ^k < e$.

$(2)$对右边的不等式用数学归纳法.$n=1$是平凡的.设$n=k$时该不等式已经成立，则当$n=k+1$时就有

$$e\left( \dfrac{k+1}{2} \right) ^{k+1} =e\left( \dfrac{k}{2} \right) ^k \cdot \left( 1+\dfrac{1}{k} \right) ^k \cdot \dfrac{k+1}{2} > (k+1)! ,$$

其中利用了$e\left( \dfrac{k}{2} \right) ^k > k!$的归纳假设和对每一个$k$有$\left( 1+\dfrac{1}{k} \right) ^k > 2$.

证$2$：$(1)$利用习题$69$中的$x_k =\left( 1+\dfrac{1}{k} \right) ^k < e$，取$k=1,2,\cdots ,n-1$并边边相乘，就有

$$x_1 x_2 \cdots x_{n-1} =\dfrac21 \cdot \left( \dfrac32 \right) ^2 \cdot \cdots \cdot \left( \dfrac{n}{n-1} \right) ^{n-1} =\dfrac{n^n }{n!} < e^{n-1} ,$$

整理后得到比本题左边更强的不等式$e\left( \dfrac{n}{e} \right) ^{n} < n!$.

$(2)$利用习题$69$中的$y_k =\left( 1+\dfrac{1}{k} \right) ^{k+1} > e$，于是有

$$y_1 y_2 \cdots y_{n-1} =x_1 x_2 \cdots x_{n-1} \cdot \left( \dfrac21 \cdot \dfrac32 \cdot \cdots \cdot \dfrac{n}{n-1} \right) =\dfrac{n^{n+1}}{n!} > e^{n-1} ,$$

这样就得到

$$n! < en\left( \dfrac{n}{e} \right) ^n =e\left( \dfrac{n}{2} \right) ^n \cdot n\left( \dfrac{2}{e} \right) ^n .$$

这里的情况要复杂一点.首先利用$2 < e$和习题$60$知道上式右边的第二个因子$n\left( \dfrac{2}{e} \right) ^n \to 0$，因此当$n$充分大时本题的右边不等式成立.用数学归纳法可以证明当$n\geqslant 6$时$n\left( \dfrac{2}{e} \right) ^n < 1$，然后对于$n=1$到$5$作计算，可知这时不等式也是成立的.

$75$.证明不等式：

$(a)\;\dfrac{1}{n+1} < \ln \left( 1+\dfrac{1}{n} \right) < \dfrac{1}{n} $，其中$n$为任何正整数.

$(b)\;1+\alpha < e^{\alpha }$，其中$\alpha $为异于零的实数.

证：$(a)$引用习题$69$中的记号和结论，由于该题中的数列$\lbrace x_n \rbrace $严格单调递增收敛，数列$\lbrace y_n \rbrace $严格单调递减收敛，它们的极限都是$e$，因此就对每一个$n$成立不等式

$$x_n =\left( 1+\dfrac{1}{n} \right) ^n < e < y_n =\left( 1+\dfrac{1}{n} \right) ^{n+1} .$$

取自然对数，并利用函数$\ln x$的严格单调递增性，再加整理就可得到所要的不等式.

$(b)$首先指出可以从习题$69$得出稍弱一点的不等式$e^{\alpha } \geqslant 1+\alpha (\alpha \neq 0)$.

分$\alpha > 0$和$\alpha < 0$两种情况来证明.

若$\alpha > 0$且为有理数，可设$\alpha =\dfrac{p}{q} $，其中$p,q$都是正整数，则从习题$69$知道有

$$e > \left( 1+\dfrac{1}{q} \right) ^q ,$$

然后利用幂函数$x^{\frac{p}{q} } $在$x > 0$时严格单调递增，就有

$$e^{\alpha } =e^{\frac{p}{q} } > \left( 1+\dfrac{1}{q} \right) ^p > 1+\dfrac{p}{q} =1+\alpha .$$

对于$\alpha < 0$的情况，由于$\alpha \leqslant -1$时表达式$1+\alpha $已经小于等于$0$，可见只要在$-1 < \alpha < 0$的条件下来证明即可.设$\alpha =-\dfrac{p}{q} $，其中$p,q$为正整数，且有$q > 1$.

从习题$69$知道对于大于$1$的正整数$q$有

$$e < \left( 1+\dfrac{1}{q-1} \right) ^q ,$$

然后利用负指数的幂函数$x^{-\frac{p}{q} } $在$x > 0$时严格单调递减，就有

$$e^{\alpha } =e^{-\frac{p}{q} } > \left( 1+\dfrac{1}{q-1} \right) ^{-p} =\left( 1-\dfrac{1}{q} \right) ^p > 1-\dfrac{p}{q} =1+\alpha .$$

（在$\alpha > 0$时最后一步只要用二项式定理，但在$-1 < \alpha < 0$时的最后一步需要用到的是习题$7$中的伯努利不等式.）

这样就已经对于所有不等于$0$的有理数$\alpha $得到了$e^{\alpha } > 1+\alpha $.对于$\alpha $为无理数的情况，可以取一个有理数列$\lbrace \alpha_n \rbrace $，使得$\alpha_n \to \alpha $，然后对于不等式$e^{\alpha_n } > 1+\alpha_n $取极限（其中包括代入法命题$1.4$）就可以得到

$$e^{\alpha } \geqslant 1+\alpha \quad (\alpha \neq 0).\label{2} \tag{2}$$

下面证明在$\eqref{2}$中不可能成立等号.其中的主要工具就是前面已经证明过的习题$76$中的极限等式.

用反证法.分$-1 < \alpha < 0$和$\alpha > 0$两种情况来证明.

$(1)$设有某个$\alpha_0 \in (-1,0)$使得$e^{\alpha_0 } =1+\alpha_0 $成立.这时

$$\begin{align}
e^{\alpha_0 +\frac{1}{n} } -1-\left( \alpha_0 +\dfrac{1}{n} \right) & =(1+\alpha_0 )(e^{\frac{1}{n} } -1) -\dfrac{1}{n} \\
& =\dfrac{(1+\alpha_0 ) \cdot n(e^{\frac{1}{n}} -1) -1}{n} .
\end{align}$$

在习题$76$中令$a=e$，可见上面的最后一个分式的分子当$n\to \infty $的极限为$\alpha_0 < 0$，因此当$n$充分大时上述分式小于$0$.这样就证明了当$n$充分大时，对于$\alpha =\alpha_0 +\dfrac{1}{n}$来说，得到了与不等式$\eqref{2}$相矛盾的结果.因此$-1 < \alpha < 0$时其中不可能成立等号.

$(2)$现在设有某个$\alpha_1 > 0$，使得$e^{\alpha_1 } =1+\alpha_1 $成立.这时

$$\begin{align}
e^{\alpha_1 -\frac{1}{n} } -1-\left( \alpha_1 -\dfrac{1}{n} \right) & =(1+\alpha_1 )(e^{-\frac{1}{n} } -1) +\dfrac{1}{n} \\
& =\dfrac{(1+\alpha_1 ) \cdot n(e^{-\frac{1}{n}} -1) +1}{n} .
\end{align}$$

同样利用习题$76$（令其中的$a=e^{-1}$），可见上式的最后一个分式的分子当$n\to \infty $的极限为$-\alpha_1 < 0$，因此当$n$充分大时上述分式小于$0$.这样就证明了当$n$充分大时，对于$\alpha =\alpha_1 -\dfrac{1}{n} $来说，得到了与不等式$\eqref{2}$相矛盾的结果.因此当$\alpha > 0$时其中也不可能成立等号.

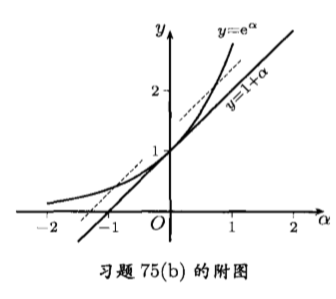
注$\quad $最后对于上述解法的来历作一点解释.学过导数的读者不难看出，上述解法的第二步，即证明$\eqref{2}$中不可能成立等号，其中的思想方法来自于曲线$y=e^{\alpha }$的切线斜率在$\alpha > 0$时大于$1$，而在$\alpha < 0$时小于$1$.同时$y=1+\alpha $是斜率恒等于$1$的直线.

如左图所示，于$\alpha \neq 0$时$e^{\alpha } > 1+\alpha $，同时如两条虚线所示，如果曲线$y=e^{\alpha }$与斜率为$1$的直线相交（$\alpha \neq 0$），则就不可能完全在该直线的上方.这就是上述证明的几何背景.

$76$.求证：

$$\lim_{n\to \infty } n\left( a^{\frac{1}{n}} -1\right) =\ln a\quad (a > 0),$$

式中$\ln a$是取$e=2.718\cdots $作底时，数$a$的对数.

证：本题是$0\cdot \infty $型的不定式.作代换$u_n =a^{\frac{1}{n}} -1$，于是有$u_n \to 0$，同时得到

$$n\left( a^{\frac{1}{n}} -1\right) =\ln a\cdot \dfrac{u_n }{\ln (1+u_n )} ,$$

从而转换为$\dfrac{0}{0}$型的不定式，并只需要证明$\displaystyle \lim_{n\to \infty } \dfrac{\ln (1+u_n )}{u_n } =1$.

利用习题$71$的两个结论就可以推出当$u_n \to 0$时有

$$\lim_{n\to \infty } (1+u_n )^{\frac{1}{u_n }} =e.$$

（这里又将问题转化为$1^{\infty }$型的不定式.）最后用代入法命题$1.4$就得到所要求的

$$\lim_{n\to \infty } \dfrac{\ln (1+u_n )}{u_n } =\lim_{n\to \infty } \ln [(1+u_n )^{\frac{1}{u_n }}] =\ln e =1.$$

下面介绍习题$146$和$147$.由于它们与数$e$密切有关，而与其前后的许多习题没有多少联系，因此将它们放在这里介绍.

$146$.证明：数列

$$x_n =1+\dfrac12 +\dfrac13 +\cdots +\dfrac{1}{n} -\ln n \quad (n=1,2,\cdots )$$

收敛，从而有公式

$$1+\dfrac12 +\dfrac13 +\cdots +\dfrac{1}{n} =C+\ln n +\varepsilon_n ,$$

式中$C=0.577216\cdots $称为欧拉常数，且当$n\to \infty $时$\varepsilon_n \to 0$.

证：利用习题$75(a)$的不等式：$\dfrac{1}{k+1} < \ln (1+\dfrac{1}{k} ) < \dfrac{1}{k} $，就有

$$0 < \dfrac{1}{k} -\ln (1+\dfrac{1}{k}) < \dfrac{1}{k} -\dfrac{1}{k+1} .$$

在上式中取$k$从$1$到$n$并相加，得到

$$0 < y_n \overset{def}{=} 1+\dfrac12 +\cdots +\dfrac{1}{n} -\ln (n+1) < 1-\dfrac{1}{n+1} < 1.$$

又由于

$$y_{n+1} -y_n =\dfrac{1}{n+1} +\ln (n+1) -\ln (n+2) =\dfrac{1}{n+1} -\ln (1+\dfrac{1}{n+1}) > 0,$$

故数列$\lbrace y_n \rbrace $单调递增有上界，因此收敛.又可以发现有

$$x_n =1+\dfrac12 +\cdots +\dfrac{1}{n} -\ln n =y_n +\ln \dfrac{n+1}{n} .$$

利用$0 < \ln \dfrac{n+1}{n} < \dfrac{1}{n}$并结合$\lbrace y_n \rbrace $收敛，可见$\lbrace x_n \rbrace $收敛.记其极限为$C$，就得到

$$1+\dfrac12 +\cdots +\dfrac{1}{n} -\ln n=C+\varepsilon_n ,$$

其中$\varepsilon_n \to 0$.

$147$.求$\displaystyle \lim_{n\to \infty } \left( \dfrac{1}{n+1} +\dfrac{1}{n+2} +\cdots +\dfrac{1}{2n} \right) $.

解$1$由上一题的公式得到

$$1+\dfrac12 +\dfrac13 +\cdots +\dfrac{1}{n} =C+\ln n+\varepsilon_n ,$$

$$1+\dfrac12 +\dfrac13 +\cdots +\dfrac{1}{2n} =C+\ln 2n +\varepsilon_{2n} .$$

两式相减得到

$$\dfrac{1}{n+1} +\dfrac{1}{n+2} +\cdots +\dfrac{1}{2n} =\ln 2+\varepsilon_{2n} -\varepsilon_n ,$$

令$n\to \infty $，可见上式左边的极限为$\ln 2$.

解$2$不用欧拉常数的知识，可以直接用习题$75(a)$中的不等式求本题的极限.

记$x_n =\dfrac{1}{n+1} +\dfrac{1}{n+2} +\cdots +\dfrac{1}{2n} $.取$k=1,2,\cdots ,n$，则可以从习题$75(a)$得到下列$n$个不等式：

$$\ln \dfrac{2n+1}{n+1} < x_n < \ln \dfrac{2n}{n} =\ln 2.$$

将上式左边改写为$\ln \dfrac{2n+1}{n+1} =\ln 2-\ln (1+\dfrac{1}{2n+1} ) $，令$n\to \infty $，并用夹逼定理就得到$\displaystyle \lim_{n\to \infty } x_n =\ln 2$.