本章引入复数和复变函数的基本概念.

复数最早出现在卡尔达诺（G.Cardano，$1501-1576$）的名著《大术》（$1545$）中.他把复数看成是无价值的、不合用的，并称$i=\sqrt{-1}$这样的数为虚数.第一个认识到虚数价值的人是邦贝利（R.Bombelli，$1526-1572$），他用虚数解不可约三次代数方程，并给出一些最简单的复数运算法则.但是，即使$17$世纪的大数学家对虚数的代数性质和几何性质都是不清楚的，甚至认为是不可思议的.牛顿（Isaac Newton，$1642-1727$）把虚数排斥在数的概念之外，而莱布尼茨（Gottfried Wilhelm Leibniz，$1646-1716$）则说：“复数是精神世界的一个奇妙的避难所，好像是存在又不存在的两栖物.”直到$19$世纪，复数才具有现代的含义.

复数

数

$$z=x+iy$$

称为复数，其中$x$和$y$是实数，而$i$是虚单位，$i^2=-1$.实数$x$和$y$分别称为复数$z$的实部和虚部，并记为：

$$x={\rm Re}\,z,y={\rm Im}\,z.$$

两个复数相等是指它的实部和虚部分别相等，即等式

$$x_1 +iy_1 =x_2 +iy_2 $$

相当于两个等式：

$$x_1 =x_2 ,y_1 =y_2 .$$

由于在直角坐标系中，当且仅当两个点具有相等的横坐标和相等的纵坐标时才会重合，所以平面上的全部点可以与所有复数间建立一一对应的关系.换言之，我们将借助于横坐标为$x$，纵坐标为$y$的点来表示复数$z=x+iy$，这样的平面称为复平面$\mathbb{C}$.表示数$z$的点通常称为点$Z$.复数可以用向量来表示，使复数的实部与虚部对应于向量的横坐标与纵坐标（图$1.1$）.

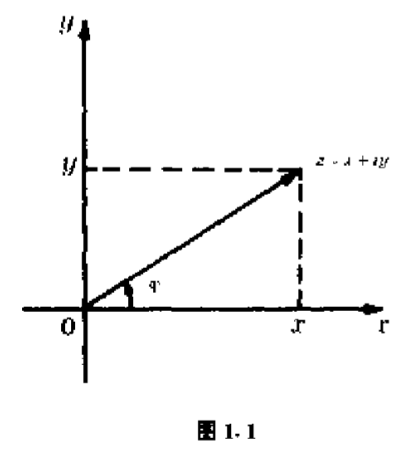
我们将虚部等于零的复数$x+i0$和它的实部看做是一样的：$x+i0=x$，并认为实数是复数的特殊情况.用$Ox$轴上的点表示实数，称此轴为实轴.类似地，实部等于零的复数写为$0+iy=iy$，称为纯虚数，用$Oy$轴上的点来表示它们，并称这个轴为虚轴.

复数$z$的位置也可用极坐标来确定，也就是借助对应于复数的向量的长度$r$，和这个向量与实轴正向的夹角$\varphi $来确定.数$r$和$\varphi $分别称为复数$z$的模和辐角，记为

$$r=\vert z\vert ,\varphi ={\rm Arg}\,z.$$

这里引进的模的概念是实数的绝对值的概念的推广.实数的模就是它的绝对值，纯虚数的模就是它的虚部的绝对值.

由模和辐角的定义推出，若$z=x+iy$，则

$$\begin{equation}
\begin{split}
x & =r\cos{\varphi } =\vert z\vert \cos{({\rm Arg}\;z)} ,\
y & =r\sin{\varphi } =\vert z\vert \sin{({\rm Arg}\;z)}
\end{split}
\end{equation} \label{1.1} \tag{1.1} $$

和

$$\vert z\vert =r=\sqrt{x^2+y^2},$$

$$\tan{({\rm Arg}\,z)} =\tan{\varphi } =\dfrac{y}{x} .$$

值得注意的是，辐角${\rm Arg}\,z$是多值的，它们之间可以相差$2\pi $的整数倍，通常取由不等式

$$0\leqslant {\rm Arg}\,z < 2\pi $$

所确定的值作为辐角的主值，$z$的辐角的主值记为$\arg{z}$，于是我们有

$${\rm Arg}\,z=\arg{z}+2k\pi (k为整数).\label{1.2} \tag{1.2}$$

例如，当$z$是正实数时，$\arg{z}=0$；当$z$是负实数时，$\arg{z} =\pi $；当$z$是具有正虚部的纯虚数时，$\arg{z} =\dfrac{\pi }{2} $.但是注意，$0$的幅角是没有意义的.

利用公式$\eqref{1.1}$，可以把任何异于零的复数表达为复数$z$的三角形式：

$$z=x+iy=r(\cos{\varphi } +i\sin{\varphi } ).\label{1.3} \tag{1.3}$$

例如，

$$\begin{array}{l}
1 =1(\cos{0} +i\sin{0}) ,\\
i=1\left( \cos{\dfrac{\pi }{2}} +i\sin{\dfrac{\pi }{2}} \right) , \\
1+i=\sqrt{2} \left( \cos{\dfrac{\pi}{4}} +i\sin{\dfrac{\pi }{4}} \right) ,\\
-2=2(\cos{\pi } +i\sin{\pi } ).
\end{array}$$

借助于欧拉公式$e^{i\varphi } =\cos{\varphi } +i\sin{\varphi } $（见本书第六章$\S 1$），可以把复数$z$的三角形式$\eqref{1.3}$化为指数形式：

$$z=re^{i\varphi } .\label{1.4} \tag{1.4}$$

复数$z=x+iy$的共轭复数定义为$\overline{z} =x-iy$.彼此共轭的复数关于实轴是对称的.

彼此共轭的复数的模是相同的，而辐角相差一个符号：

$$\vert \overline{z} \vert =\vert z\vert ,\arg{\overline{z}} =-\arg{z} .$$

任何实数与它自己共轭.

复数的四则运算

将算术的加法和乘法规则运用于复数，我们有

$$\begin{array}{l}
(x_1 +iy_1 )+(x_2 +iy_2 )=(x_1 +x_2 )+i(y_1 +y_2 ), \\
(x_1 +iy_1 )(x_2 +iy_2 )=(x_1 x_2 -y_1 y_2 )+i(x_1 y_2 + x_2 y_1 ).
\end{array} \label{1.5} \tag{1.5} $$

第二个恒等式中，我们使用了关系式$i^2=-1$.

复数的减法定义为加法的逆运算，由此得到

$$(x_1 +iy_1 )-(x_2 +iy_2 )=(x_1 -x_2 )+i(y_1 -y_2 ).$$

特别地，由式$\eqref{1.5}$推出，两个彼此共轭的复数的乘积是实数，等于该复数的模的平方：

$$(x+iy)(x-iy)=x^2+y^2$$

或

$$z\overline{z} =\vert z\vert ^2 .$$

两个彼此共轭的复数的和也是实数：

$$(x+iy)+(x-iy)=2x$$

即

$$z+\overline{z} =2{\rm Re} z.$$

$(1)$复数加法和减法的几何意义

若用向量表示复数，则复数的实部和虚部就是向量的坐标.因为向量的相加或相减就是它们的坐标对应地相加或相减，于是复数的相加或相减归结为相应向量的相加或相减，图$1.2$展现了复数加法和减法的几何意义.

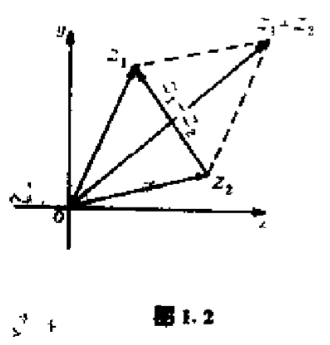
由于复数的模等于对应向量的长度，所以两个复数的和的模不大于两个复数的模的和：

$$\vert z_1 +z_2 \vert \leqslant \vert z_1 \vert +\vert z_2 \vert .$$

接连使用几次这个不等式，便得到

$$\vert z_1 +z_2 +\cdots +z_n \vert \leqslant \vert z_1 \vert +\vert z_2 \vert +\cdots +\vert z_n \vert .$$

当且仅当表示数$z_1 ,z_2 ,\cdots ,z_n $的向量在一条直线上，且指向同一方向，即当

$$\arg{z_1 } =\arg{z_2 } =\cdots =\arg{z_n } $$

时，等式成立.

$(2)$圆的方程

由复数减法的几何意义，若$z_0 $是给定的复数，$\rho $是给定的实数，则满足方程

$$\vert z-z_0 \vert =\rho $$

的点的全体形成以$z_0 $为中心以$\rho $为半径的圆周，不等式$\vert z-z_0 \vert < \rho $确定这圆周内的点集，而不等式$\vert z-z_0 \vert > \rho$确定圆周外的点集.

$(3)$复数的乘除法

复数的除法定义为乘法的逆运算.利用共轭数的性质，按下述方法进行复数的除法是方便的：首先把分子和分母乘以分母的共轭数，于是分母变为正实数，然后分别用分母除所得分子的实部和虚部：

$$\begin{align}
\dfrac{x_1 +iy_1 }{x_2 +iy_2 } & =\dfrac{(x_1 +iy_1 )(x_2 -iy_2 )}{(x_2 +iy_2 )(x_2 -iy_2 )} \\
& =\dfrac{(x_1 x_2 +y_1 y_2 )+i(x_2 y_1 -x_1 y_2)}{x_2^2 +y_2^2 } \\
& =\dfrac{x_1 x_2 +y_1 y_2 }{x_2^2 +y_2^2 }+i\dfrac{x_2 y_1 -x_1 y_2 }{x_2^2 +y_2^2 } .
\end{align}$$

若利用复数的三角形式：

$$\begin{array}{l}
z_1 =r_1 (\cos{\varphi_1 } +i\sin{\varphi_1 } ), \\
z_2 =r_2 (\cos{\varphi_2 } +i\sin{\varphi_2 } ).
\end{array}$$

则得到，

$$\begin{align}
z_1 z_2 & =r_1 r_2 [(\cos{\varphi_1} \cos{\varphi_2 } -\sin{\varphi_1 } \sin{\varphi_2 } )+i(\cos{\varphi_1 } \sin{\varphi_2 } +\sin{\varphi_1 } \cos{\varphi_2 })] \\
& =r_1 r_2 [\cos{(\varphi_1 +\varphi_2 )} +i\sin{(\varphi_1 +\varphi_2 )}] ,\label{1.6} \tag{1.6}
\end{align}$$

因而复数相乘就是它们的模相乘，而辐角相加：

$$\begin{array}{l}
\vert z_1 z_2 \vert =\vert z_1 \vert \vert z_2 \vert , \\
{\rm Arg}\,(z_1 z_2 )={\rm Arg}\,z_1 +{\rm Arg}\,z_2 .
\end{array}$$

注意，后一等式的两端是多值的，所以应理解为等式左端的值的集合和它的右端的值的集合完全一样.

$(4)$复数乘法的几何意义

表示乘积$z_1 z_2 $的向量可以这样得到：把表示数$z_1 $的向量绕正向旋转角度$\varphi_2 $，再把它的长度乘以$\vert z_2 \vert $.例如，数$i$的模等于$1$，辐角等于$\dfrac{\pi }{2} $，所以复数$\alpha $乘$i$归结为把$\alpha $按正向旋转$90^{\circ}$，而不改变其长度.

用三角式表示除法的公式为

$$\dfrac{z_1 }{z_2 } =\dfrac{r_1 }{r_2 } [\cos{(\varphi_1 -\varphi_2 ) }+i\sin{(\varphi_1 -\varphi_2 )}],$$

即

$$\left\vert \dfrac{z_1 }{z_2} \right\vert =\dfrac{\vert z_1 \vert }{\vert z_2 \vert } ;{\rm Arg}\,\dfrac{z_1 }{z_2 } ={\rm Arg}\,z_1 -{\rm Arg}\,z_2 .$$

乘方与开方

设$z=r(\cos{\varphi} +i\sin{\varphi })$.由乘法规则得

$$z^n =r^n (\cos{n\varphi } +i\sin{n\varphi }) ,$$

即

$$\vert z^n \vert =\vert z\vert ^n ,{\rm Arg}\,(z^n) =n{\rm Arg}\,z\label{1.7} \tag{1.7}$$

利用除法规则，不难验证这公式对于负整数$n$也成立.

在$r=1$的特殊情况下，我们有

$$(\cos{\varphi } +i\sin{\varphi })^n =\cos{n\varphi } +i\sin{n\varphi } ,\label{1.8} \tag{1.8} $$

利用二项式定理

$$(\cos{\varphi } +i\sin{\varphi })^n =\cos{}^n \varphi +ni\cos{}^{n-1} \varphi \sin{\varphi} +\cdots +ni^{n-1} \cos{\varphi } \sin{}^{n-1} \varphi +i^n \sin{}^n \varphi .\label{1.9} \tag{1.9} $$

将$\eqref{1.8}$和$\eqref{1.9}$结合起来，我们就可以得到通过$\cos{\varphi }$和$\sin{\varphi }$表达$\cos{n\varphi }$或$\sin{n\varphi }$的表达公式.

例如，当$n=3$时

$$\begin{align}
\cos{3\varphi } +i\sin{3\varphi } & =(\cos{\varphi } +i\sin{\varphi })^3 \\
& =\cos{}^3 \varphi +3i\cos{}^2 \varphi \sin{\varphi } -3\cos{\varphi } \sin{}^2 \varphi -i\sin{}^3 \varphi .
\end{align}$$

比较两边的实部和虚部，我们得到

$$\begin{align}
\cos{3\varphi } & =\cos{}^3 \varphi -3\cos{\varphi } \sin{}^2 \varphi \\
& =4\cos{}^3 \varphi -3\cos{\varphi } \label{1.10} \tag{1.10}
\end{align}$$

及

$$\begin{align}
\sin{3\varphi } & =3\cos{}^2 \varphi \sin{\varphi } -\sin{}^3 \varphi \\
& =-4\sin{}^3 \varphi +3\sin{\varphi } .\label{1.11} \tag{1.11}
\end{align}$$

通过到复数域的旅行，我们很容易地得到了实数域的两个结果.$n$越大，这种方法的优越性就越明显，这使我们回忆起近代著名数学家哈达玛（Jacques Hardamard，$1865-1963$）的一句名言：实域中两个真理之间的最短路程是通过复域.

下面我们转而研究求方根的问题.

设$n$是正整数.求$z$的$n$次方根就是求这样的数：$\omega =\sqrt[n]{z}$，它的$n$次方等于$z$.根据乘方法则得

$$\vert \omega \vert ^n =\vert z\vert ,n{\rm Arg}\,\omega ={\rm Arg}\,z.$$

令$\omega =\rho (\cos{\theta } +i\sin{\theta})$，并考虑到复数的辐角含有$2\pi $的整数倍的未确定项，则有

$$\rho^n =r,n\theta =\varphi +2k\pi (k=0,\pm 1,\pm 2,\cdots ),$$

从而

$$\rho =\sqrt[n]{r} ,\theta =\dfrac{\varphi +2k\pi }{n} ,$$

这里根式下取的是算术根.这样一来，

$$\begin{align}
\sqrt[n]{z} & =\sqrt[n]{r(\cos{\varphi } +i\sin{\varphi })} \\
& =\sqrt[n]{r} \left( \cos{\dfrac{\varphi +2k\pi }{n}} +i\sin{\dfrac{\varphi +2k\pi }{n}} \right) .\label{1.12} \tag{1.12}
\end{align}$$

虽然$k$是任意整数，但由这个公式只能得到$n$个不同的值，并且这$n$个不同的值可通过令$k=0,1,2,\cdots ,n-1$而得到.

公式$\eqref{1.12}$表明，所有这些不同的根都具有相同的模$\sqrt[n]{\vert z\vert }$，相邻两个值的辐角差为$2\pi /n$.由此我们知道，任何复数$z\neq 0$的$n$次方根都有$n$个不同的值，而且这些值可以被排成内接于圆$\vert \omega \vert =\sqrt[n]{\vert z\vert }$的一个正$n$边形的$n$个顶点（图$1.3$）.

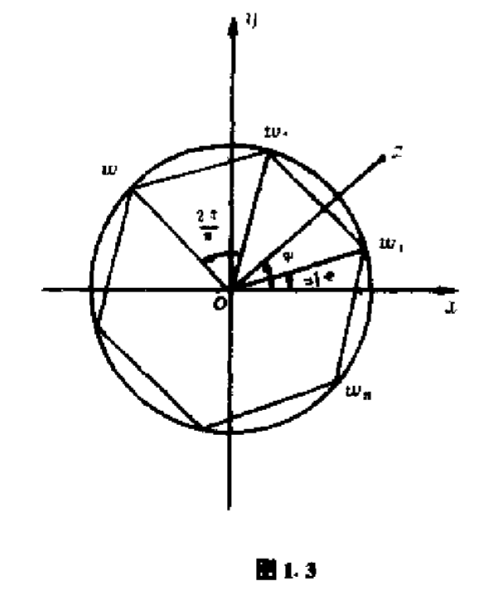
由此我们还知道，$n$次方程

$$z^n +\alpha =0\label{1.13} \tag{1.13}$$

可解，这里$\alpha $是任意的复数，并且知道，这个方程有$n$个不同的值.

单位根

求数$1$的$n$次根是一种特别重要的情形.这个根有$n$个值，所有这些值我们都叫做$n$次单位根.由等式

$$1=\cos{0} +i\sin{0} $$

与公式$\eqref{1.12}$，得

$$\sqrt[n]{1} =\cos{\dfrac{2k\pi }{n}} +i\sin{\dfrac{2k\pi }{n}} ,k=0,1,\cdots ,n-1.\label{1.14} \tag{1.14} $$

由式$\eqref{1.14}$知，当$n$为偶数时，在$k=0$与$\dfrac{n}{2}$时得$n$次单位根的实值；当$n$为奇数时，仅在$k=0$时才能得出实值.在复平面上，$n$次单位根排列在单位圆的圆周上，而且把圆周分为$n$等分，其中一个分点是数$1$.因此，$n$次单位根中那些不是实数的值的位置关于实轴对称.换言之，它们两两共轭.

二次单位根有两个值$1,-1$.四次单位根有四个值$1,-1,i$和$-i$.三次单位根有三个数，除去$1$以外，是共轭数

$$\begin{array}{l}
\omega =\cos{\dfrac{2\pi }{3}} +i\sin{\dfrac{2\pi }{3}} =-\dfrac{1}{2} +i\dfrac{\sqrt{3}}{2} ,\\
\omega^2 =\cos{\dfrac{4\pi }{3}} +i\sin{\dfrac{4\pi }{3}} =-\dfrac{1}{2} -i\dfrac{\sqrt{3}}{2} .
\end{array}\label{1.15} \tag{1.15}$$

三次根的值经常用到，应当记住.

这里指出，复数$\alpha $的$n$次方根的所有值，都可从它的某一个值乘上所有的$n$次单位根来得出.事实上，设$\beta $是$\alpha $的$n$次根的某一个值，即$\beta^n =\alpha $，而$\varepsilon $为任一$n$次单位根，即$\varepsilon^n =1$.则$(\beta \varepsilon )^n =\beta^n \varepsilon^n =\alpha $，即$\beta \varepsilon $为$\sqrt[n]{\alpha }$的一个值.用$\beta $乘$n$次单位根的每一个值，就得出$\alpha $的$n$次根的$n$个不同的值，即这个根的所有的值.

例如，数$-8$的立方根有一个是$-2$，由式$\eqref{1.15}$知，它的其它两个根是

$$-2\omega =1-i\sqrt{3} ,-2\omega^2 =1+i\sqrt{3} .$$