在这一节中，我们将要介绍复变函数论的一些最基本的概念.复变函数，它的极限，连续性等，这些概念来自实变量函数论中的相应概念.

几何概念

复平面上的一个点集$D$叫做一个区域，若它具有两个性质：

$(1)$在$D$中的每一个点必有一个以这个点为圆心的充分小的圆，同它一起都属于这个集合；这个性质称为开集性.

$(2)$ $D$中的任何两个点都可用一条由$D$的点所构成的折线连接起来；这个性质称为连通性.

复平面上点的邻域可作为区域的最简单的例子.所谓一个点$a$的$\varepsilon $邻域，是指以$a$为圆心，以$\varepsilon $为半径的一个开圆，即满足不等式

$$\vert z-a\vert < \varepsilon $$

的那些点的集合.

凡本身不属于区域$D$，而在它的任何邻域内都含有属于$D$的点的那种点叫做$D$的边界点.区域$D$的所有边界点的集合叫做$D$的边界.区域$D$连同它的边界合在一起的集合，叫做闭区域，用记号$\overline{D} $来表示.

复自变量函数

设函数$\omega =f(z)$定义在复平面$\mathbb{C}$的某一点集$E$上，对于$E$的每个点$z$，都有$\omega $的一个或多个值与之对应，就说在点集$E$上给定了函数$\omega =f(z)$.若每一个点$z$只有一个$\omega $值与之对应，则$\omega $称为$z$的单值函数，如有多个$\omega $值与之对应，则称$\omega $为$z$的多值函数.

例如，函数$\omega =z^2$是单值的，它定义在整个复平面$\mathbb{C}$上.函数$\omega ={\rm Arg}\,z$是多值的，在全平面上除去点$z=0$外是有定义的.

给定复数$z$相当于给定两个实数$x$和$y\colon z=x+iy$.同样地，$\omega $也对应着两个实数$u$和$v\colon \omega =u+iv$.这样一来，复变函数$\omega $和复自变量$z$之间的关系$\omega =f(z)$相当于两个关系：

$$\begin{array}{l}
u=u(x,y), \\
v=v(x,y).
\end{array} \label{2.1} \tag{2.1}$$

它确定实数值$u$和$v$为自变量$x$和$y$的函数.

例如，若$\omega =z^2$，则令$z=x+iy,\omega =u+iv$，得到

$$\begin{align}
u+iv & =(x+iy)^2 \\
& =(x^2-y^2)+2ixy,
\end{align}$$

因而等式$\omega =z^2 $相当于等式

$$u=x^2-y^2 ,v=2xy.$$

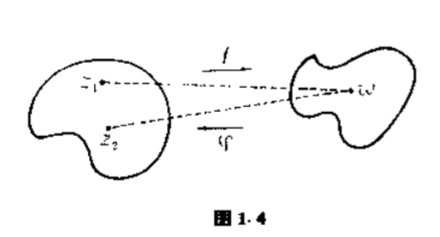
以某一个平面上的点表示自变量$z$的值，这个平面称为“$z$平面”；而以另一个平面上的点表示函数$\omega $的值，这个平面称为“$\omega $平面”.函数$\omega =f(z)$确定了$z$平面的点和$\omega $平面的点的对应，换言之，函数实现了由$z$平面的点到$\omega $平面的相应点的映射或变换.设函数$\omega =f(z)$在区域$D$上是单值的，并把$z$平面上的区域$D$映射到$\omega $平面上的区域$G$的内部.如果进一步假定在映射$\omega =f(z)$之下，$D$的两个不同点对应于$G$的两个不同点，那么这个映射就称为在$D$上是一一的，或者单叶的.

设已经给定了一个把区域$D$映射到区域$G$上去的函数$\omega =f(z)$.如果有一个函数$z=\varphi (\omega )$，它使得$G$中的每一个点$\omega $，都与所有那些由函数$\omega =f(z)$映到点$\omega $的点$z$成对应，那么这个函数$z=\varphi (\omega )$就叫做函数$\omega =f(z)$的反函数（图$1.4$）.不难看出，当$f$同$\varphi $这两个函数都是单值函数时，而且也只有在这时，映射$f$是一一的.

在弄清了映射的概念后，我们来研究在映射下曲线的变化.

我们知道，在平面上曲线可以用参数方程来表示.设$x(t)$、$y(t)$是变数$t$的实连续函数，$t$在区间$\alpha \leqslant t \leqslant \beta $上变化.方程

$$\begin{cases}
x=x(t), \\
y=y(t),
\end{cases} \alpha \leqslant t\leqslant \beta \label{2.2} \tag{2.2}$$

给出一条连续曲线的参数表示式.例如，以原点为中心、$r$为半径的圆具有如下的参数表示式

$$\begin{cases}
x=r\cos{\theta }, \\
y=r\sin{\theta},
\end{cases} 0 \leqslant \theta \leqslant 2\pi \label{2.3} \tag{2.3} $$

假如我们令$z=x+iy$，使$z(t)=x(t)+iy(t)$，则曲线的分析表达式可以写成一个方程

$$z=z(t),\alpha \leqslant t \leqslant \beta .$$

例如圆$\eqref{2.3}$的方程可写为

$$z=z(\theta )=r(\cos{\theta } +i\sin{\theta } ),0\leqslant \theta \leqslant 2\pi .$$

借助于复数的指数表示，我们又可将圆$\eqref{2.3}$的方程写为

$$z=re^{i\theta } ,0\leqslant \theta \leqslant 2\pi .\label{2.4} \tag{2.4} $$

圆的这种方程使用起来非常方便.

一般说来，在映射$\omega =f(z)$下，曲线的像仍是曲线，我们通过具体实例来说明这一点.

例$1\quad $考虑映射$\omega =e^{i\theta } z$.

这个映射定义在全平面，是单值的，并且是单叶的.由复数乘法的几何意义知道，这是一个绕原点转动$\theta $角度的旋转，在这个映射之下，过原点的直线变为过原点的直线，以原点为心的圆变为以原点为心的圆.其它的曲线也都绕原点旋转一个$\theta $角度.

例$2\quad $考虑映射

$$\omega =\dfrac{1}{2} \left( z+\dfrac{1}{z} \right) .\label{2.5} \tag{2.5} $$

儒可夫斯基函数.

这个映射对于一切$z\neq 0$都是单值的.现在我们来求它的单叶性区域.为此目的，我们假定$z_1 $与$z_2 $在映射$\eqref{2.5}$下变成同一点$\omega $，于是

$$z_1 +\dfrac{1}{z_1 } =z_2 +\dfrac{1}{z_2 } ,$$

$$(z_1 -z_2 )\left( 1-\dfrac{1}{z_1 z_2 } \right) =0,$$

由此有

$$z_1 =z_2 或z_1 z_2 =1.$$

因此，在任何区域内，要映射$\eqref{2.5}$是单叶映射的充分且必要的条件是，该区域内没有任何两点$z_1 $与$z_2 $能有关系$z_1 z_2 =1$.例如，单位圆的内部$\vert z\vert < 1$，或它的外部$\vert z\vert > 1$，都满足这个条件.我们指出，映射$\eqref{2.5}$把单位圆的内部$\vert \vert < 1$映到$\omega $平面上线段$[-1,1]$的外部.为此设

$$z=re^{i\theta } ,\omega =u+iv .(0 < r < 1)$$

代入$\eqref{2.5}$，得

$$u+iv=\dfrac12 \left( r\cos{\theta } +ir\sin{\theta } +\dfrac{1}{r} \cos{\theta } -\dfrac{i}{r} \sin{\theta } \right) ,$$

分开实部和虚部，得到方程组

$$\begin{cases}
u=\dfrac12 \left( r+\dfrac{1}{r} \right) \cos{\theta } ,\\
v=\dfrac12 \left( r-\dfrac{1}{r} \right) \sin{\theta } .
\end{cases} \label{2.6} \tag{2.6} $$

在$z=re^{i\theta }$中，固定$r=r_0 < 1$，让$\theta $从$0$变到$2\pi $，得到单位圆内的一个圆.在映射$\eqref{2.5}$下，它的像在$\omega $平面上是一个椭圆.这只要在公式$\eqref{2.6}$中消去参数$\theta $，就能得出这个椭圆的标准方程：

$$\dfrac{u^2}{\dfrac14 \left( r_0 +\dfrac{1}{r_0 } \right) ^2} +\dfrac{v^2}{\dfrac14 \left( r_0 -\dfrac{1}{r_0 } \right) ^2} =1.\label{2.7} \tag{2.7}$$

它的两个半轴分别是

$$a=\dfrac12 \left( r_0 +\dfrac{1}{r_0 } \right) ,b=\dfrac12 \left( r_0 -\dfrac{1}{r_0 } \right) .$$

当$\theta $从$0$变到$2\pi $时，通过$u$、$v$符号的改变可看出，上半圆周映为下半椭圆，下半圆周映为上半椭圆.并且对于任意的$r_0 $都有

$$c=\sqrt{a^2-b^2} =1.$$

所以，所有这些椭圆都是共焦的，焦点为$\pm 1$（图$1.5$）.

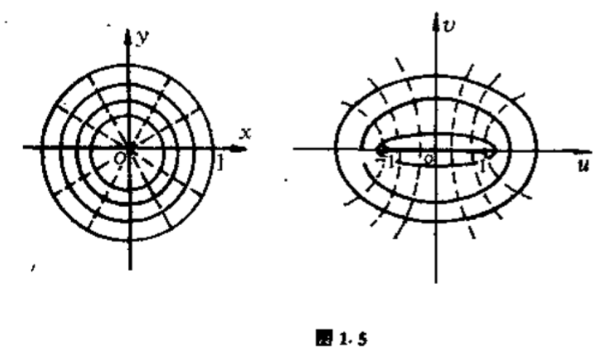
当$r_0 \to 1$时，$a\to 1,b\to 0$，椭圆“压缩”到实轴上的线段$[-1,1]$；当$r_0 \to 0$时，$a\to \infty ,b\to \infty $，椭圆无限变大.这样一来，当$r_0 $在区间$(0,1)$中变化时，这些椭圆扫过除线段$[-1,1]$外的整个复平面，这就是单位圆内部在映射$\omega $下的像区域.

用研究单位圆内的任一条半径的像的办法同样可以得出这一结论.

在$z=re^{i\theta }$中，固定$\theta =\theta_0 $，让$r$从$0$变到$1$，得到单位圆内的一条半径，和$x$轴正向的交角为$\theta $，它的像是$\omega $平面上的半条双曲线.从$\eqref{2.6}$消去参数$r$就得到双曲线的标准方程：

$$\dfrac{u^2}{\cos{}^2 \theta_0 } -\dfrac{v^2}{\sin{}^2 \theta_0 } =1\label{2.8} \tag{2.8} $$

双曲线的实半轴$a=\vert \cos{\theta_0 } \vert $，虚半轴$b=\vert \sin{\theta_0 } \vert $.当$\theta_0 $变动时，我们得到不同的双曲线.所有这些双曲线都是共焦的，焦点是$\pm 1$.下面我们来看一看这些双曲线的具体位置.

利用$\eqref{2.6}$式不难看出下述结果.

当$\theta_0 =0$时，$v=0,1 < u < +\infty $.

当$\theta_0 =\dfrac{\pi }{2}$时，$u=0,-\infty < v < 0$.

当$\theta_0 =\pi $时，$v=0,-\infty < u < -1$.

当$\theta_0 =\dfrac{3}{2} \pi $时，$u=0,0 < v < +\infty $.

当$\theta_0 $在第一象限时，$\cos{\theta_0 } < u < +\infty $，$-\infty < v < 0$.这是半条双曲线，位于第四象限，不带顶点.

当$\theta_0 $在第四象限时，$\cos{\theta_0 } < u < +\infty $，$0 < v < +\infty $.这是位于第一象限的单支双曲线，不带顶点（图$1.5$）.

当$\theta_0 $位于二、三象限时，读者不难得出类似结论.由此我们又可得出结论：单位圆内部在映射$\omega $下的像区域是整个复平面去掉线段$[-1,1]$.

我们建议读者采用上述办法研究一下，在映射$\omega $下，单位圆的外部的像区域是什么.

例$2$提供了平面区域间映射的一个具体实例，它告诉我们如何将去掉一段直线，或者说有裂缝的平面映射到单位圆的内部或外部.第二章我们还会再次遇到这个函数，并将它应用到具体问题中去.

序列的极限

设$z_0 $是一个有限复数.含$z_0 $的任何区域称为$z_0 $的邻域.不过我们只用圆邻域.满足不等式

$$\vert z-z_0 \vert < \rho $$

的点的全体称为点$z_0$的$\rho $邻域.

对于$\infty $，我们把任意大的半径的圆外称为它的邻域，即对任意大的$A > 0$，满足

$$\vert z\vert > A$$

的点的全体称为$\infty $的邻域.

有了邻域的概念，我们来定义点列的极限.

称有限复数$z_0 $是点列$z_1 ,z_2 ,\cdots ,z_n ,\cdots $的极限，如果对于任意给定的、不管多么小的$\varepsilon > 0$，总能找到这样的正整数$N$，使得当$n \geqslant N$时，不等式$\vert z_n -z_0 \vert < \varepsilon $成立，记为

$$\lim_{n\to \infty } z_n =z_0 .$$

若$z_n =x_n +iy_n $，$z_0 =x_0 +iy_0 $，并且考虑到等式

$$\vert z_n -z_0 \vert =\sqrt{(x_n -x_0 )^2+(y_n -y_0 )^2} ,$$

则由极限定义不难得出如下结论：极限

$$\lim_{n\to \infty } z_n =z_0 $$

存在相当于两个实的极限

$$\lim_{n\to \infty }x_n =x_0 ,$$

$$\lim_{n\to \infty } y_n =y_0 $$

存在.

称点列$z_1 ,z_2 ,\cdots ,z_n ,\cdots $趋于$\infty $，并记为

$$\lim_{n\to \infty } z_n =\infty .$$

如果对于不管多么大的正数$M$，总能找到这样的正整数$N$，使得当$n\geqslant N$时，不等式$\vert z_n \vert > M$成立.

一个点列$z_1 ,z_2 ,\cdots ,z_n ,\cdots $，有时也简记为$\lbrace z_n \rbrace $.我们也用序列一词.在序列中有些项可能是相同的，这是与点列不同的地方.

一个序列（或点列）有有限极限$z_0 $，我们称这个序列（或点列）是收敛的.它没有极限，或者以$\infty $为极限，则称它是发散的.

函数的极限，连续性

在有了序列极限的定义后，就可以定义函数的极限了.

当$z\to z_0 $时，称函数$f(z)$以$\omega_0 $为极限，如果对不管多么小的$\varepsilon > 0$，总能找到一个$\delta > 0$，使得当$0 < \vert z-z_0 \vert < \delta $时，总有$\vert \omega -\omega_0 \vert < \varepsilon $成立.记为

$$\omega_0 =\lim_{z\to z_0 } f(z).$$

例如，$f(z)=z^2$.当$z\to i$时，

$$z^2 \to i^2 =-1.$$

当$z_0 $是$\infty $，或$\omega $是$\infty $，或两者都是$\infty $时，按无穷远点邻域的定义改写上面的定义.

例如，对$\omega_0 \neq 0$，等式

$$\lim_{z\to \infty } f(z)=\omega_0 $$

表示对于任意的$\varepsilon > 0$，总有$A > 0$，使得满足$\vert z\vert > A$的一切$z$，函数$f(z)$满足不等式

$$\vert f(z)-\omega_0 \vert < \varepsilon .$$

称函数$f(z)$在$z_0 $是连续的，如果

$$\lim_{z\to z_0 } f(z)=f(z_0 ).$$

即任给$\varepsilon > 0$，总存在$\delta > 0$，使得当$\vert z-z_0 \vert < \delta $时，

$$\vert f(z)-f(z_0 )\vert < \varepsilon $$

成立.

例如$f(z)=z^2$在每一点$z_0 $处连续.