哈尔莫斯说，问题是数学的心脏.正是好的数学问题促进了数学的蓬勃发展.数字史上最早、最著名的问题是古希腊的几何三大难题：三等分任意角、立方倍积、化圆为方，还有正多边形作图问题.这些问题引起了历代数学家热切关注，并大大地推动了数学的发展.到$19$世纪，这些问题才得以彻底解决，并促进了代数数、超越数理论和伽罗瓦理论的诞生.

三大几何难题

从中学时代我们已经熟知，在欧几里得几何中几何作图的工具是直尺与圆规.这里的尺子与通常的尺子不同，通常用的尺子上面有刻度，而几何的直尺是没有刻度的，我们只能用它去作连接给定两点的直线.欧几里得圆规也要与两脚规加以区别.欧几里得圆规只是为了以给定的点为圆心，通过定点而画圆用的.

仅用直尺与圆规的作图是一个非常古老的课题，早在古希腊时代已经开始研究了.当时希腊人提出了三个著名的问题，后来被称为三大几何难题，它们是：

$(1)$化圆为方$\quad $给定一个圆，求作一个面积与它相等的正方形；

$(2)$三等分任意角$\quad $给定一个角，求作两条线三等分这个角；

$(3)$立方倍积$\quad $给定一个立方体，求作体积为这立方体体积两倍的立方体.

希腊人不会解这些问题，我们也不必惊奇，因为这些问题都是不可解的.也就是说，不能用直尺和圆规把它们的图作出来.要证明问题$(2)$与$(3)$都是不可解的并不困难，我们将在后面给出.但要证明问题$(1)$不可解就不那么简单了，我们只能给出一些说明.奇妙的是，证明这三大难题不可解的工具在本质上不是几何的而是代数的，所以在代数还没有发展到相当的水平时是不可能解决这些问题的.

但是，正是在研究这些问题的过程中促进了数学发展.两千多年来，三大几何难题引起了许多数学家的兴趣，对它们的深入研究不但给予希腊几何学以巨大影响，而且引出了大量的新发现.例如，许多二次曲线、三次曲线以及几种超越曲线的发现；后来又有关于有理数域、代数数与超越数、群论等的发展.在化圆为方的研究中几乎从一开始就促进了穷竭法的发展，而穷竭法正是微积分的先导.

实数域

我们最熟悉的数是实数，用$\mathbb{R}$来表示全体实数的集合.实数有两种基本的运算，一种是加法，一种是乘法；减法和除法分别是加法和乘法的逆运算.

实数的加法和乘法满足一些性质，我们将它们总结如下：设$a$、$b$、$c$是$\mathbb{R}$中的数.

性质$1$

$(1)a+(b+c)=(a+b)+c$；

$(2)a+b=b+a$；

$(3)$存在唯一的元素$0\in \mathbb{R} $，使得$a+0=a$；

$(4)$对任意的$a\in \mathbb{R}$，都存在唯一的$x\in \mathbb{R} $，使得$a+x=0$.

性质$2$

$(1)a(bc)=(ab)c$；

$(2)ab=ba$；

$(3)$存在唯一的元素$1\in \mathbb{R} $，使得$a1=a$；

$(4)$对任意的$a\in \mathbb{R} $，$a\neq 0$，存在唯一的$y\in \mathbb{R}$，使得$ay=1$.

性质$3$

$$a(b+c)=ab+ac.$$

现代数学的研究范围大大超过了实数集，而研究广泛得多的数学对象.在许多更一般的数集中也可引进加与乘的运算，并且具有上述所述的诸性质，所以有必要抽象出一个一般的概念来概括所有这些研究对象.

代数学家们把满足这些性质的体系叫做域.这样一来，域就是普通的算术律在它里面成立的一个系统.

读者不难看出，上面所述的算术律在全体有理数的集合中是成立的，所以全体有理数域对加法和乘法构成一个域，这个域叫做有理数域，用$\mathbb{Q}$表示.

通常用$(-a)$来表示性质$1(4)$中的$x$，用$a^{-1}$表示性质$2(4)$中的$y$.这样一来，$a+(-a)=0$，$aa^{-1}=1$.

由下面的式子

$$b-a=b+(-a),$$

$$\dfrac{b}{a} =ba^{-1} (只要a\neq 0)$$

分别定义减法和除法.

根据性质$2$的$(4)$，$0$不能作除数，这样一来，表达式$x/0$没有意义.

二次扩域

给定$\mathbb{R}$的一个子集$F$，我们如何确定$F$是不是一个域呢？因为$\mathbb{R}$是一个域，所以关于域的大部分性质，如结合律、交换律等，$F$中的元素自然是满足的，需要验证的只是，若$x$、$y$是$F$的两个元素，是否$x+y$、$x-y$、$xy$、$x/y$也都是$F$的元素，对后者要求是$y\neq 0$.

设$F$是$\mathbb{R}$的一个域，$k > 0$是$F$的一个元素.我们知道$\sqrt{k} \in \mathbb{R}$，今假定$\sqrt{k}$不属于$F$.

我们称集合

$$F(k)=\lbrace a+b\sqrt{k} \colon a,b\in F\rbrace $$

为$F$的一个二次扩张.

例如，

$$\mathbb{Q} (2)=\lbrace a+b\sqrt{2} \colon a,b\in \mathbb{Q} \rbrace $$

就是有理数域$\mathbb{Q}$的一个二次扩张.

定理$1\quad $设$F$是$\mathbb{R}$的一个子域，$k$是$F$的一个正元素，而$\sqrt{k}$不在$F$内，则$F$的二次扩张$F(k)$也是一个域.

证明$\quad $容易证明，若$x$、$y$是$F(k)$的元素，则$x+y$、$x-y$、$xy$也是$F(k)$的元素.问题在于证明，对任意的$x\neq 0$，有$x^{-1} \in F(k)$.

记$x=a+b\sqrt{k}$，这里$a\in F$，$b\in F$.

首先指出，$x=0$的充要条件是$a=b=0$.事实上，当$x=0$时，必有$a=-b\sqrt{k}$.于是若$a=0$，则$b=0$；若$b=0$，则$a=0$；$b\neq 0$（或$a\neq 0$）的情况不可能出现，因为这时将有$\sqrt{k} =-\dfrac{a}{b} \in F$，这与假设是相矛盾的.

若$x\neq 0$，则必有$a\neq 0$或$b\neq 0$，从而$a^2-b^2 k\neq 0$，进而有$a-b\sqrt{k}\neq 0$，这样一来，

$$\begin{align}
x^{-1} & =\dfrac{1}{a+b\sqrt{k}} =\dfrac{a-b\sqrt{k}}{(a+b\sqrt{k})(a-b\sqrt{k})} \\
& =\dfrac{a}{a^2-b^2k} -\dfrac{b\sqrt{k}}{a^2-b^2k} .
\end{align}$$

因为$F$是一个域，所以$a/(a^2-b^2k)$、$-b\sqrt{k} /(a^2-b^2k)$都属于$F$.由于推出$x^{-1} \in F$.定理证毕.

由数$0$与$1$经过有限次的加、减、乘、除（零不能作除数）以及对正数的开方运算后得到的数称为二次不尽根.

例如，数

$$x=1+\sqrt{2+\sqrt{1+\sqrt{5}}} $$

就是一个二次不尽根.

定义$\quad $设$F_0 ,F_1 ,\cdots ,F_n $都是$\mathbb{R}$的子域，再设$F_0 =\mathbb{Q}$是有理数域，而且每一个域$F_k $都是域$F_{k-1}$的二次扩张（$k=1,2,\cdots ,n$），则称$F_n $是一个$n$阶的二次域.

由上面的定理不难看出，每个二次不尽根，都属于某一个阶的二次域.

设$a,b,c\in F$，$c > 0$，$\sqrt{c} \overline{\in} F$.考虑数

$$a+b\sqrt{c} \in F(c).$$

设$x=a+b\sqrt{c}$，则数$a-b\sqrt{c}$叫做数$x$的共轭数，记为$\overline{x} \colon \overline{x} =a-b\sqrt{c}$.

容易验证，共轭数具有如下的简单性质：

$(a)x=0\Leftrightarrow \overline{x}=0$；

$(b)x\overline{x} =a^2-cb^2$；

$(c)x=\overline{x} \Leftrightarrow x=a$；

$(d)z=x+y\Rightarrow \overline{z} =\overline{x} +\overline{y} $；

$(e)z=xy\Rightarrow \overline{z} =\overline{z} \overline{y}$；

$(f)z=x^n \Rightarrow \overline{z} =(\overline{x} )^n$.

这些性质与共轭复数的性质相同.在中学学复数时，我们曾有这样一个定理：实系数方程的共轭根是成对出现的.这里我们也有一个类似的定理.

定理$2\quad $设

$$P(x)=a_0 x^n +a_1 x^{n-1} +\cdots +a_{n-1} x+a_n $$

是一$n$次多项式，它的系数$a_0 ,a_1 ,\cdots ,a_n $都属于同一个由实数构成的域$F$.若$x_0 \in F(c)$是多项式$P(x)$的一个根，则$\overline{x}_0 $也是$P(x)$的一个根，即

$$P(x_0 )=0\Rightarrow P(\overline{x}_0 )=0.$$

证明$\quad $由假设

$$a_0 x_0^n +a_1 x_0^{n-1} +\cdots +a_{n-1} x_0 +a_n =0.$$

利用共轭的性质，两边取共轭，则有

$$a_0 \overline{x}_0^n +a_1 \overline{x}_0^{n-1} +\cdots +a_{n-1} \overline{x}_0 +a_n =0,\label{1.1} \tag{1.1} $$

这就是要证的.

系$\quad $设$a_1 ,a_2 ,a_3 $属于由实数构成的域$F$.若三次多项式

$$x^3 +a_1 x^2 +a_2 x+a_3 =0\label{1.2} \tag{1.2} $$

在二次扩张$F(c)$中有一个根，则它一定在$F$中还有一根.

证明$\quad $由代数基本定理，方程$\eqref{1.2}$在复数域中有三个根，不妨设有$x_1 ,x_2 ,x_3 $.由韦达定理（见第五章$\S 1$，式$(1.6)$），

$$x_1 +x_2 +x_3 =-a_1 \in F.$$

若$x_1 \in F(c)$，则由定理$2$，$\overline{x}_1 $也是方程$\eqref{1.2}$的根，不妨设$x_2 =\overline{x}_1 $.由共轭的定义，$x_1 +x_2 \in F$.这样一来，

$$x_3 =-a-(x_1 +x_2 )\in F,$$

定理得证.

系指出，若方程$\eqref{1.2}$在$F$没有根，则它在$F(c)$中也不会有根.

我们将把系应用到$F$是有理数域的情况，即假定方程$\eqref{1.2}$的系数都是有理数，在这种情况下，如果方程$\eqref{1.2}$没有有有理根，则它不会有二次不尽根.

不难看出，有理数的$n$次代数方程可化为整系数的$n$次代数方程.事实上，只要乘上系数分母的最小公倍数就行了.我们还需要下面的定理.

定理$3\quad $若整系数的$n$次方程

$$a_0 x_n +a_1 x^{n-1} +\cdots +a_{n-1} x+a_n =0\label{1.3} \tag{1.3} $$

有有理根$\dfrac{a}{b}$（是既约分数），则$a$是$a_n $的因数，$b$是$a_0 $的因数.

证明$\quad $将$\dfrac{a}{b}$代入方程$\eqref{1.3}$，得

$$a_0 \dfrac{a^n}{b^n} +a_1 \dfrac{a^{n-1}}{b^{n-1}} +\cdots +a_{n-1} \dfrac{a}{b} +a_n =0,$$

$$a_0 a^n +a_1 a^{n-1} b+\cdots +a_{n-1} ab^{n-1} +a_n b^n =0,$$

$$a(a_0 a^{n-1} +a_1 a^{n-2} b+\cdots +a_{n-1} b^{n-1})=-a_n b^n,$$

因为$a$与$b$是互素的，所以$a$是$a_n $的因数.类似地，用提出公因数$b$的方法可证明，$b$是$a_0 $的因数.

现在将上面的讨论应用到两个特殊的方程上去.

例$1\quad $证明方程

$$x^3 =2\label{1.4} \tag{1.4}$$

没有二次不尽根的解.

证明$\quad $由定理$2$的系，我们只需证明这个方程没有有理根.如果方程$\eqref{1.4}$有有理根$\dfrac{a}{b}$，则由定理$3$，$a$是$2$的因数，$b$是$1$的因数，因而它的有理根不外是$1$，$-1$，$2$，$-2$.直接验证就知道它们都不是.这样一来，方程$\eqref{1.4}$没有有理根，从而也没有二次不尽根的解.

例$2\quad $证明方程

$$8x^3-6x-1=0\label{1.5} \tag{1.5} $$

没有二次不尽根的解.

证明$\quad $如果方程$\eqref{1.5}$有有理根$\dfrac{a}{b}$，则$a$是$1$的因子，$b$是$8$的因子.这样一来，方程$\eqref{1.5}$的有理根不外是$\pm 1$，$\pm \dfrac{1}{2}$，$\pm \dfrac{1}{4}$，$\pm \dfrac{1}{8}$，直接难知道它们都不是，由定理$2$的系，方程$\eqref{1.5}$没有二次不尽根的解.

代数数与超越数

考虑有理系数的多项式

$$a_0 x^n +a_1 x^{n-1} +\cdots +a_{n-1} x+a_n =0,$$

凡是这样方程的实数根都称为代数数，不是代数数的实数称为超越数.

代数数显然是存在的.是不是所有的实数都是代数数呢？不是的，超越数是存在的，例如数$e$和$\pi $都是超越数.抽象地证明超越数的存在性并不困难，但要具体地证明某一个特定的数，例如$e$和$\pi $是超越数，那是非常困难的.下面我们来证明超越数的存在性.

我们从集合的计数开始.如果集合$S$中只含有有限个元素，我们很清楚如何把它数出来.不妨设这个集合有$n$个元素.用数学语言来表示，数集合$S$中的元素的个数的过程就是建立自然数集合$\lbrace 1,2,\cdots ,n\rbrace $与$S$的元素之间的一一对应的过程.换言之，如果存在一个双方单值的一一映射（下面称这种映射为双射）

$$f\colon \lbrace 1,2,3,\cdots ,n\rbrace \to S,$$

我们就说集合$S$有$n$个元素.

对无限集合如何计数呢？我们引进势的概念.设集合$A$、$B$都含有无限多个元素.如果存在一个双射$f\colon A\to B$，就说集合$A$与$B$有相同的势.如果一个集合$S$与全体自然数的集合有相同的势，就称它是可数的.这就是说，对于集合$S$中的每一个元素都能指定一个不同的自然数与之对应.即$S$的元素可安排为一个序列：

$$N\colon 1,2,3,\cdots ,n,\cdots $$

$$S\colon x_1 ,x_2 ,x_3 ,\cdots ,x_n ,\cdots $$

例如，所有整数构成的集合是可数集.因为我们可以把整数排成如下的顺序：

$$0,-1,+1,-2,+2,\cdots ,$$

更精确些，由公式

$$f(n)=\dfrac{n-1}{2} ,n为奇数,$$

$$f(n)=-\dfrac{n}{2} ,n为偶数,$$

所定义的函数$f$建立了全体自然数与全体整数间的一一对应.

这个例子说明，一个集合能和它自身的一个真子集等势.当然这只能在无限集中才可能.可见，无限集与有限集有着很大的不同.

同样的道理可以证明，如果集合$A$和$B$是可数的，则它们的并$A\cup B$也是可数的.因为$A$能表示成为$A=\lbrace a_1 ,a_2 ,\cdots \rbrace $，同样，$B=\lbrace b_1 ,b_2 ,\cdots \rbrace $.因此$a_1 $，$b_1 $，$a_2 $，$b_2 $，$\cdots $就是对$A\cup B$中元素的一种计数方式.

下面的定理给出一个更强的结果.

定理$4\quad $若$A_1 ,A_2 ,\cdots $都是可数集，则$ \mathop{\cup}_{n=1}^{\infty } A_n $也是可数集.

证明$\quad $我们记$A_1 =\lbrace a_1^1 ,a_2^1 ,a_3^1 ,\cdots \rbrace $，$A_2 \lbrace a_1^2 ,a_2^2 ,a_3^2 ,\cdots \rbrace $，$\cdots $，$A_n =\lbrace a_1^n ,a_2^n ,a_3^n ,\cdots \rbrace $，$\cdots $.因而$a_k^j $是集合$A_j $的第$k$个元素.定义$j+k$为$a_k^j$的高度，于是$a_1^1$是高度为$2$的唯一元素；同样，$a_2^1$和$a_1^2$是高度为$3$的仅有的元素；依此类推.由于对于任一正整数$m\geqslant 2$，高度为$m$的元素只有$m-1$个，所以我们可将$\mathop{\cup}_{n=1}^{\infty } A_n $的元素按其高度排成

$$a_1^1 ,a_1^2 ,a_2^1 ,a_3^1 ,a_2^2 ,a_1^3 ,\cdots $$

或者排成下面的阵列，按箭头所指的顺序去数它们：

$$\begin{matrix}
a_1^1 & & a_2^1 & \to & a_3^1 & & a_4^1 & \cdots \\
\downarrow & \nearrow & & \swarrow & & \nearrow & & & \\
a_1^2 & & a_2^2 & & a_3^2 & & a_4^2 & \cdots \\
& \swarrow & & \nearrow & & & & \\
a_1^3 & \to & a_2^3 & & a_3^3 & & a_4^2 & \cdots \\
\cdots & & & & & & &
\end{matrix}$$

用这种方法可以数出每一个$a_k^j$.这就证明了定理.

这个定理说的是，可数个可数集的并是可数的.自然地，可数个有限集的并也是可数的.

我们有下面的重要推论：

系$\quad $有理数集是可数集.

证明$\quad $由于有定理$4$，我们只需证明在区间$(0,1)$上的有理数集是可数的就行了.但是，在$(0,1)$上的任一有理数都属于某一级的法瑞序列（见第三章$\S 1$）.读者不难根据法瑞序列的顺序建立$(0,1)$间的全体有理数与全体自然数间的双射.

定理$5\quad $全体代数数所组成的集合是可数的.

证明$\quad $在$1.3$节我们已经指出，只要考虑整系数方程就行了.设整系数的$n$次方程为

$$a_0 x^n +a_1 x^{n-1} +\cdots +a_{n-1} x+a_n =0,$$

这里$a_0 ,a_1 ,\cdots ,a_n $都是整数.命

$$N=n+\vert a_0 \vert +\vert a_1 \vert +\cdots +\vert a_n \vert ,$$

显然$N\geqslant 2$.对同一个$N$，只有有限个多项式，每一个多项式的根数也有限.所以对应于同一个$N$的代数数也是有限的.这些代数数所有的集用$E_N$来表示.现在把它们排列如下：

$$E_2 ,E_3 ,\cdots ,E_N ,\cdots $$

显然，每一个代数数必属于某个$E_k $中.上面的各集合可能有交.为此考虑集合$E_N^1 \colon E_N^1$表示在$E_N$中而不在$E_2 ,E_3 ,\cdots ,E_{N-1} $中的数所组成的集合.这样一来，我们得到

$$E_2 ,E_3^1 ,\cdots ,E_N^1 ,\cdots $$

这是可数个有限集.由定理$4$可知，定理$5$成立.

一个无限集如果不是可数的，就称它是不可数的.粗略地说，一个不可数集的元素“太多”了，多到使得我们不能把它们安排在一个序列里.

下面的定理不但告诉我们超越数是存在的，而且还告诉我们，超越数比代数数要“多得多”.

定理$6\quad (0,1)$间实数所成的集是不可数集.

证明$\quad $若定理不成立，则可设$(0,1)$间的实数可排成一个序列：

$$x_1 ,x_2 ,\cdots ,x_n ,\cdots ,$$

我们将$x_n $表示成十进制小数

$$x_n =0.a_{n1} a_{n2} a_{n3} a_{n4} \cdots ,$$

我们造一个数$y\in (0,1)$，使得

$$y=0.b_1 b_2 b_3 b_4 \cdots ,$$

其中$b_n $由下式定义

$$b_n =\begin{cases} 8 , & a_{nn} \neq 8, \\ 1, & a_{nn} =8.\end{cases} $$

这个数$y$与序列中的任何一个数都不同，它不在序列中.这是一个矛盾.它指出$(0,1)$间的实数是不可数的.

这个定理的直接推论就是，超越数是存在的.法国数学家刘维尔（Joseph Liouville，$1809-1882$）在$1844$年第一次证明了超越数的存在性.令人感兴趣的是，超越数的存在性的上述证明是非构造性的.我们知道它存在，而且很多，但是，不知道它们都在哪儿！无怪乎在集合论的创始者康托（Georg Cantor,$1845-1918$）证明了这个定理的时候，人们以一种相当不欢迎的情绪来接受它.

自然对数和底$e$与$\pi $都是超越数.证明它们都是超越数是困难的，并吸引着许多数学家付出巨大的劳动去进行研究.直到$1873$年埃尔米特（Charles Hermite,$1822-1901$）才给出了$e$是超越数的证明.他认为证明$\pi $的超越性更困难，他不敢去尝试.他给友人的信中写道：“我不敢去试着证明$\pi $的超越性.如果其他人承担这些工作，对于他们的成功没有比我更高兴的人了.但请相信我，我亲爱的朋友，这决不会不使他们花去一些力气”.$9$年之后，林德曼（Ferdinand Lindemann,$1852-1939$）在$1882$年用实质上与埃尔米特相同的方法证明了$\pi $的超越性.

直尺圆规作图

现在回到直尺圆规作图问题.在用直尺和圆规的一切作图中最终都取决于求

$(1)$两个圆的交点；

$(2)$两个直线的交点；

$(3)$一条直线与一个圆的交点.

借助于解析几何，我们可以容易地把前面的讨论与几何作图问题联系起来.取初始点为$(0,0)$与$(0,1)$.我们可以用直尺与圆规作出其他点，其坐标我们都可以通过解两个联立方程来得到，其中每一个方程都是下述两种形式的一种：

$$Ax+By+C=0$$

或

$$x^2+y^2+Dx+Ey+F=0.$$

这里的系数$A$、$B$、$C$、$D$、$E$、$F$都以一种简单的方式依赖于已经作出来的点的坐标.而解这种方程所用的运算只是加、减、乘、除以及正数的开方.由此我们得到如下的重要结论：借助直尺圆规可以构造的点的坐标一定可以从$0$、$1$出发通过有限次的加、减、乘、除以及正数开平方根的运算以后而得到.这些点是平面上坐标为有理数或二次不尽根的那些点.

三等分任意角

如图$4.1$所示，我们从$60^{\circ}$角着手.

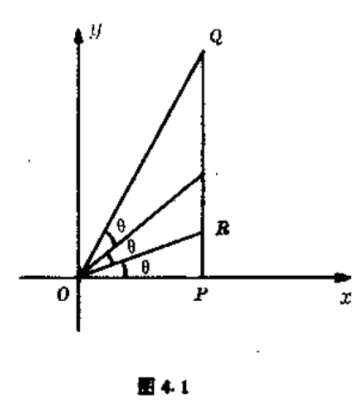
设$\angle QOP=60^{\circ}$，并设线段$OP$的长度为$1$.假定三等分任意角是可能的.如图设$\angle ROP=20^{\circ}$.那么，点$R$的纵坐标一定是有理数或二次不尽根.这相当于说$\cos{\theta } =1/OR$是有理数或二次不尽根.在第一章我们曾得到公式（见第一章式$(1.10)$），

$$\cos{3\theta} =4\cos{}^3 \theta -3\cos{\theta} ,$$

现在$\cos{3\theta } =\cos{60^{\circ}} =\dfrac12 $，所以

$$4\cos{}^3 \theta -3\cos{\theta} =\dfrac12 ,$$

令$x=\cos{\theta }$并代入上式，得到

$$8x^3-6x-1=0.$$

这正是前面讨论过的方程$\eqref{1.5}$.这个方程没有有理根，也没有二次不尽根.这说明我们的假定是不对的.这就证明了三等分任意角是不可能的.

立方倍积

现在考虑立方倍积问题.设给定的立方体是单位立方体，它的两个相邻顶点间的距离是单位长度.设体积为这立方体体积两倍的立方体的相邻顶点间的距离为$x$，则有

$$x^3=2$$

或

$$x^3-2=0.$$

如果立方倍积问题可解，我们必须能用直尺和圆规构造出长度为$\sqrt[3]{2}$的线段.但是我们在前面已经证明了，方程$\eqref{1.4}$没有有理根，也没有二次不尽根，这样一来，立方倍积问题是不可解的.

化圆为方

考虑半径为$1$的单位圆，它的面积为$\pi $，现在构造一个边长为$x$的正方形，它的面积为$\pi $，于是$x^2 =\pi $，$x=\sqrt{\pi }$.由于$\sqrt{\pi }$是一个超越数，所以它不可能是二次不尽根，因此化圆为方问题是不可解的.