福特圆的性质

福特圆是同福特（L.R.Ford）引进的一种几何图形，由某些特殊的圆组成，而这些圆又与法瑞序列密切相关.在复平面$z=x+iy$上研究这些圆更为方便.

用$C(h/k)$来表示以$h/k+i/2k^2$为中心，以$1/2k^2$为半径的圆.在复平面上这些圆有下述方程：

$$\left\vert z-\left( \dfrac{h}{k} +\dfrac{i}{2k^2} \right) \right\vert =\dfrac{1}{2k^2} ,\label{2.1} \tag{2.1} $$

它们都位于上半平面，并且都与$x$轴相切，切点是$x=h/k$.这些圆具有下述的一个重要而有趣的性质.

定理$1\quad $两个不同的福特圆从不相交.它们相切的充要条件是，在某一级法瑞序列中它们的分数是相邻分数.

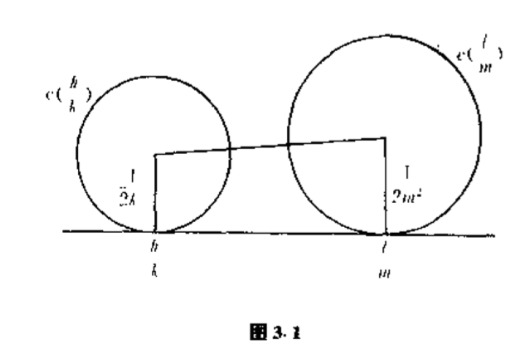
证明$\quad $如图$3.1$所示，假定有两个不同的福特圆$C(h/k)$和$C(l/m)$，其圆心分别是$h/k+i/2k^2 $和$l/m+i/2m^2$，且$hm-kl\neq 0$.设两个圆心间的距离为$d$，则

$$d^2 =\left( \dfrac{h}{k} -\dfrac{l}{m} \right)^2 +\left( \dfrac{1}{2k^2} -\dfrac{1}{2m^2} \right)^2 .$$

这两个圆的半径的和的平方是

$$t^2 =\left( \dfrac{1}{2k^2} +\dfrac{1}{2m^2} \right)^2.$$

因为

$$\begin{align}
d^2-t^2 & =\left( \dfrac{h}{k} -\dfrac{l}{m} \right)^2 -\dfrac{1}{k^2 m^2} \\
& =\dfrac{(hm-kl)^2-1}{k^2m^2} \geqslant 0,
\end{align}$$

所以这两个圆不会相交.两圆相切的充要条件是等式成立，即当且仅当$hm-kl=\pm 1$.根据$\S 1$定理$2$，$h/k$与$l/m$是某一级法瑞序列中的相邻分数.定理证毕.

在两个圆$C(h/k)$和$C(l/m)$相切的情况下，不难把切点的坐标找出来.设切点为$\omega =u+iv$.由图$3.2$，

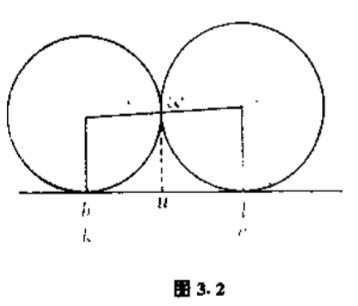
$$\dfrac{\dfrac{l}{m} -u}{u-\dfrac{h}{k} } =\dfrac{\dfrac{1}{2m^2} }{\dfrac{1}{2k^2}} =\dfrac{k^2}{m^2} ,$$

解出$u$，

$$u=\dfrac{hk+lm}{m^2+k^2} .\label{2.2} \tag{2.2} $$

值得注意的是，$u$是一个有理数.$v$的坐标也可类似地算出，结果仍是有理数.这样，我们得到一个有趣的结果：福特圆的切点具有有理坐标.

考虑$C(H/K)$，$C(h/k)$，$C(h_1 /k_1 )$，其中$0 < K < k < k_1 $，并设分数$H/K$和$h/k$在$k$级法瑞序列中是相邻分数.分数$h_1 /k_1 $不在这个法瑞序列中.如图$3.3$所示，

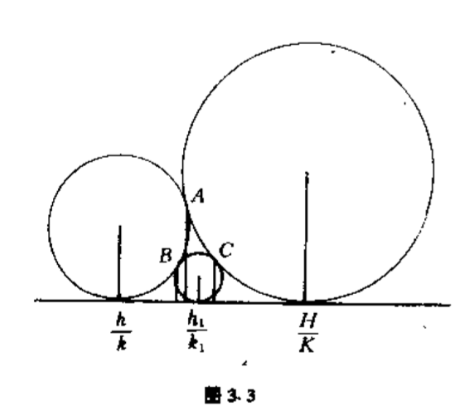
假定这三个福特圆是彼此相切的，由于分数$h_1 /k_1 $与$h/k$相邻，又与$H/K$相邻，因而它是$h/k$与$H/K$的中项：

$$\dfrac{h_1 }{k_1 } =\dfrac{H+h}{K+k} ,$$

它在更高级的法瑞序列中，并且

$$h_1 =H+h ,k_1 =K+k .\label{2.3} \tag{2.3}$$

在图$3.3$中，由三段圆弧组成的三角形，称为圆弧三角形$ABC$.

我们现在已经做好了证明定理$5$的前半段的准备工作.

定理$5$证明的完成

设$r$是一无理数.因为两福特圆的切点的坐标都是有理数，所以直线$x=r$不会通过任何两个福特圆的公共切点.这样一来，它一定通过无穷多个圆弧三角形的内部.

设其中的一个圆弧三角形是由圆$C(h/k)$，$C(H/K)$和$C(h_1 /k_1 )$的弧组成的.我们可以假定

$$\dfrac{h}{k} < r < \dfrac{H}{K} ,\label{2.4} \tag{2.4} $$

另外还有

$$\dfrac{h}{k} < \dfrac{h_1 }{k_1 } < \dfrac{H}{K} ,\label{2.5} \tag{2.5} $$

设圆$C(h/k)$与圆$C(H/K)$的切点是$A$，圆$C(h/k)$与圆$C(h_1 /k_1 )$的切点为$B$，而圆$C(h_1 /k_1 )$与圆$C(H/K)$的切点为$C$；设$a$、$b$、$c$是$A$、$B$、$C$的$x$坐标，由式$\eqref{2.2}$，我们有

$$a=\dfrac{hk+HK}{k^2+K^2} ,b=\dfrac{hk+h_1 k_1 }{k^2+k_1^2} ,c=\dfrac{h_1 k_2 +HK}{k_1^2+K^2} .$$

这样一来，

$$\begin{align}
c-a & =\dfrac{h_1 k_2 +HK}{k_1^2+K^2} -\dfrac{hk+HK}{k^2+K^2} \\
& =\dfrac{HK(k^2 -k_1^2 )+h_1 k_1 (k^2+K^2 )-hk(k_1^2 +K^2)}{(k^2+K^2)(k_1^2 +K^2)} \\
& =\dfrac{kK(Hk-hK)+k_1 k(h_1 k-hk_1 )-Kk_1 (Hk_1 -h_1 K)}{(k^2+K^2)(k_1^2 +K^2)} ,
\end{align}$$

对上式利用$\S 1$定理$1$，可得

$$c-a=\dfrac{kK+k_1 k-Kk_1 }{(k^2+K^2)(k_1^2 +K^2)} ,$$

再利用式$\eqref{2.3}$，最后得出

$$c-a=\dfrac{kK+k^2-K^2}{(k^2+K^2)(k_1^2 +K^2)} .$$

又设

$$s=\dfrac{k}{K} ,$$

前面已设定$K < k$，所以$s > 1$，于是我们有

$$c-a=\dfrac{s^2+s-1}{K^2(s^2+1)[(s+1)^2+1]} ,$$

因为

$$s^2+s-1 > 1+1-1=1,$$

我们断定

$$c-a > 0.$$

类似地，我们有

$$\begin{align}
c-b & = \dfrac{kk_1 +Kk+Kk_1 }{(k^2+k_1^2)(k_1^2 +K^2)} \\
& =\dfrac{K^2+3Kk+k^2}{(k^2+k_1^2)(K^2+ k_1^2)} \\
& =\dfrac{s^2+3s+1}{K^2[(s+1)^2+1] [s^2+(s+1)^2]} > 0.
\end{align}$$

但是，$b-a$的符号可以为正，也可以为负.事实上，通过类似的计算，可得

$$\begin{align}
b-a & = \dfrac{k^2-kK-K^2}{(k^2+K^2)(k^2 +k_1^2)} \\
& =\dfrac{s^2-s-1}{K^2(s^2+1)[s^2+(s+1)^2]} ,
\end{align}$$

这里

$$s^2-s-1=\left( s-\dfrac12 -\dfrac{\sqrt{5} }{2} \right) \left( s-\dfrac12 +\dfrac{\sqrt{5} }{2} \right) .\label{2.6} \tag{2.6}$$

由于$s > 1$，所以

$$s-\dfrac12 +\dfrac{\sqrt{5}}{2} > \dfrac12 +\dfrac{\sqrt{5}}{2} > 0,$$

从而，$b-a$的符号与$s-\dfrac{1+\sqrt{5}}{2} $有相同的符号.现在我们来考虑$b > a$和$b < a$这两种情况.因为$s$是有理数，所以$b=a$的情况不会出现.

$(1)\;b > a$或$s > \dfrac{1+\sqrt{5}}{2}$.

在这种情况下，我们试图证明，

$$\left\vert r-\dfrac{H}{K} \right\vert < \dfrac{1}{\sqrt{5} K^2} .$$

实际上，在这种情况下，圆弧三角形的横坐标的最小值与最大值是$a$和$c$，因而我们有

$$a < r < c < \dfrac{H}{K} ,$$

从而

$$\begin{align}
0 < \dfrac{H}{K} -r < \dfrac{H}{K} -a & =\dfrac{H}{K} -\dfrac{hk+HK}{k^2+K^2} \\
& =\dfrac{k}{K(k^2+K^2)} =\dfrac{s}{K^2(s^2+1)} .
\end{align}$$

现在

$$\left( s -\dfrac{1+\sqrt{5} }{2} \right) \left( s +\dfrac{1-\sqrt{5} }{2} \right) > 0,$$

因为根据假定，第一个因子和第二个因子都是正的，这样，展开上式得

$$s^2 -\sqrt{5} s+1 > 0,$$

或者

$$s^2+1 > \sqrt{5} s,$$

$$\dfrac{s}{s^2+1} < \dfrac{1}{\sqrt{5}} ,$$

所以，在这种情况下，我们有

$$0 < \dfrac{H}{K} -r < \dfrac{1}{\sqrt{5} K^2} ,$$

这正是我们希望证明的.

$(2)b < a$或$1 < s < \dfrac{1+\sqrt{5} }{2}$.

这一次我们试图证明

$$\left\vert \dfrac{h_1 }{k_1 } -r\right\vert < \dfrac{1}{\sqrt{5} k_1^2 } .$$

在现在的假定下（图$3.4$），

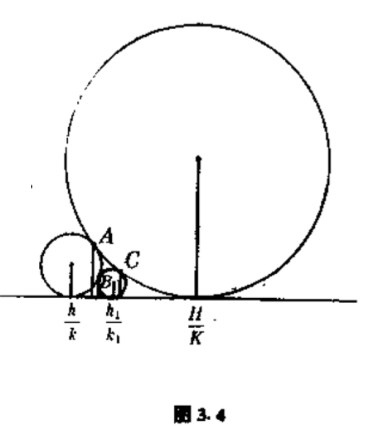
$$b < a < c,$$

因此

$$b < r < c,\label{2.7} \tag{2.7}$$

我们首先推导：

$$\dfrac{h_1 }{k_1 } -b > c -\dfrac{h_1 }{k_1 } .\label{2.8} \tag{2.8} $$

事实上，

$$\begin{align}
\dfrac{h_1 }{k_1 } -b & =\dfrac{h_1 }{k_1 } -\dfrac{hk+h_1 k_1 }{k^2 +k_1^2 } \\
& =\dfrac{k}{k_1 (k^2 +k_1^2 )} ,
\end{align}$$

而

$$\begin{align}
c- \dfrac{h_1 }{k_1 } & =\dfrac{h_1 k_1 +HK}{k_1^2 +K^2} -\dfrac{h_1 }{k_1 } \\
& =\dfrac{K}{k_1 (K^2 +k_1^2 )} ,
\end{align}$$

二者相减，我们有

$$\begin{align}
\dfrac{k}{k_1 (k^2 +k_1^2 )}- \dfrac{K}{k_1 (K^2 +k_1^2 )} & =\dfrac{(k-K)(k_1^2 -kK)}{k_1 (k^2 +k_1^2 )(K^2 +k_1^2 )} \\
& =\dfrac{k^3-K^3}{k_1 (K^2 +k_1^2 )} > 0,
\end{align}$$

这就证明了式$\eqref{2.8}$.由式$\eqref{2.7}$，我们有

$$\dfrac{h_1 }{k_1 } -c < \dfrac{h_1 }{k_1 } -r < \dfrac{h_1 }{k_1 } -b,$$

再利用式$\eqref{2.8}$，

$$\left\vert \dfrac{h_1 }{k_1 } -r\right\vert < \dfrac{h_1 }{k_1 } -b =\dfrac{k}{k_1 (k^2+k_1^2 )} =\dfrac{s(s+1)}{k_1^2 [s^2+(s+1)^2]} .$$

现在我们只需证明

$$\dfrac{s(s+1)}{s^2+(s+1)^2} < \dfrac{1}{\sqrt{5}} .$$

用反证法.假定不是这样，则有

$$\dfrac{s(s+1)}{s^2+(s+1)^2} > \dfrac{1}{\sqrt{5}} ,$$

从而

$$\sqrt{5}s(s+1) > 2s^2 +2s+1,$$

或

$$(\sqrt{5} -2)s^2+(\sqrt{5} -2)s-1 > 0,$$

或

$$\begin{align}
0 & < s^2+s-\dfrac{1}{\sqrt{5} -2} \\
& =s^2+s-(\sqrt{5} +2) \\
& =\left( s+\dfrac12 +\dfrac{2+\sqrt{5}}{2} \right) \left( s+\dfrac12 -\dfrac{2+\sqrt{5}}{2} \right) \\
& =\left( s+\dfrac32 +\dfrac{\sqrt{5}}{2} \right) \left( s-\dfrac12 -\dfrac{\sqrt{5}}{2} \right) ,
\end{align}$$

这是不可能的，因为我们已经假定了$s-\dfrac12 -\dfrac{\sqrt{5}}{2} < 0$.

这样一来，在两种情况下，我们都找到了分数$l/m$，使之满足

$$\left\vert r-\dfrac{l}{m} \right\vert < \dfrac{1}{\sqrt{5} m^2} ,\label{2.9} \tag{2.9}$$

这里分数$l/m$是由直线$x=r$所穿过的圆弧三角形$ABC$所确定的.由于这样的三角形有无穷多个，所以存在无穷多个分数$l/m$满足式$\eqref{2.9}$.这就完成了定理$5$的证明.