在$\S 3$中引入的线性方程组的等价性，以及我们不自觉地在逻辑学，在日常生活等各个方面使用的各种形态的等价性使人们想到应该一般地定义这一概念.

二元关系

设$X,Y$是任意两个集合，任意子集$\omega \subset X\times Y$叫作$X$与$Y$之间的一个二元关系.(若$X=Y$，则简称为$X$上的一个二元关系.)有序对$(x,y)\in \omega$，用记号$x\omega y$表示，并称$x$与$y$有关系$\omega$.这种记法是方便的，例如实数集$\mathbb{R}$中的顺序$<$是$\mathbb{R}$上的一个二元关系，由实平面$\mathbb{R}^2$上位于直线$x-y=0$上方的点组成(见图$7$)；用通常的不等式$x < y$代替了繁琐的包含号$(x,y)\in \omega$.

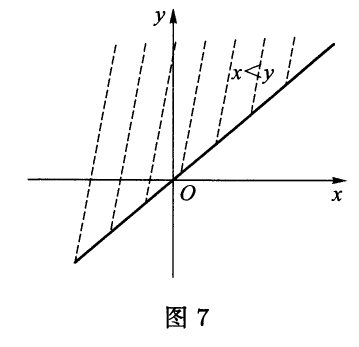
每一个函数$f:X\to Y$都对应于它的图像，也就是子集

$$\Gamma (f)=\lbrace (x,y)\mid x\in X,y=f(x)\rbrace \subset X\times Y,$$

这是$X$与$Y$之间的一个二元关系.研究函数$\mathbb{R} \to \mathbb{R}$在$\mathbb{R}^2$上的图像是数学分析的内容.显然，并非每一个二元关系都可以作为某个映射$X\to Y$的图像.二元关系成为某个映射的图像的充要条件在于，任取$x\in X$，刚好有一个元素$y$使得$x\omega y$.事实上，给定$X,Y$和图像$\Gamma (f)$，可以重建映射$f$.

等价关系

集合$X$上的二元关系$\sim$叫作等价关系，若任取$x,x’,x’’\in X$，满足关系：

$\text{i} )$ $x\sim x$(反身性)；

$\text{ii} )$ $x\sim x’ \Rightarrow x’\sim x$(对称性)；

$\text{iii} )$ $x\sim x’,x’ \sim x’’ \Rightarrow x\sim x’’$(传递性).

元素$a,b\in X$不具有等价关系记作$a \nsim b$.

与给定元素$x$等价的所有元素的子集

$$\overline{x} =\lbrace x’\in X\mid x’\sim x\rbrace \subset X$$

叫作包含$x$的等价类.由于$x\sim x$(见$(\text{i})$)，故确有$x\in \overline{x}$.任意元素$x’\in \overline{x}$都叫作类$\overline{x}$的代表元.

下述论断成立.

命题 由关系$\sim $确定的等价类的集合是集合$X$的一个划分，即$X$是这些子集的不交并(记作$\pi \sim (X)$).

证明 事实上，$x\in \overline{x}$，所以

$$X=\underset{x\in X}{\bigcup}\overline{x} .$$

现在如果$\overline{x}’\cap \overline{x}’’\neq \varnothing$且$x \in \overline{x}’\cap \overline{x}’’$，则$x\sim x’$且$x\sim x’’$，由传递性$(\text{iii})$，有$x’\sim x’’$，以及$\overline{x}’=\overline{x}’’$，这就意味着不同的等价类互不相交.$\qquad \Box$

设$\Pi=\mathbb{R}^2$是带有直角坐标系的实平面.

将两点$p,p’\in \Pi$属于同一条水平直线取作性质$\sim$，我们显然得到了一个等价关系，它的等价类是水平直线(见图$8$).

形如$xy=\rho > 0$的双曲线$\Gamma _\rho$定义了区域$\Pi _+$上的一个等价关系，其中$\Pi _+\subset \Pi$，由点$P(x,y)$，$x > 0$，$y > 0$组成(见图$9$).这些几何例子直观地说明了下述逆命题成立.

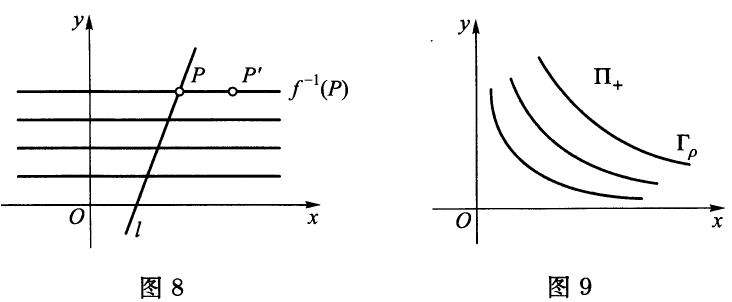
命题 如果$\pi (X)$是将集合$X$分成不相交子集$C_x$的一个划分，则$C_x$是由某一等价关系$\sim$确定的等价类.

证明 事实上，根据条件，每个元素$x\in X$仅被包含在一个子集$C_a$中.定义$x\sim x’$当且仅当$x$与$x’$属于同一个子集$C_a$.显然，这个关系是反身，对称，且传递的，即$\sim$是一个等价关系.进一步根据定义，$x\in C_a \Rightarrow \overline{x}=C_a$.所以$\pi (X)=\pi \sim (X)$.$\qquad \Box$

商映射

由于上述给出的集合$X$的等价关系与划分之间的一一对应，对应于等价关系$\sim$的划分通常记作$X/\sim$，并称之为$X$关于$\sim$的商集(或由关系$\sim$确定的商集).满射

$$p:x\mapsto p(x)=\overline{x} \label{1} \tag{1}$$

叫作$X$到商集$X/\sim$上的自然映射(或典范投影).

设$X,Y$是两个集合，且$f:X\to Y$是一个映射.二元关系$\omega _f$：

$$\forall x,x’\in X,\qquad x\omega _f x’\Leftrightarrow f(x)=f(x’)$$

显然是反身的($f(x)=f(x)$)，对称的($f(x’)=f(x)\Rightarrow f(x)=f(x’)$)，并且还是传递的($f(x)=f(x’)$和$f(x’)=f(x’’)\Rightarrow f(x)=f(x’’)$).这样$\omega _f$是$X$上的一个等价关系.对应的等价类$\overline{x}$就是在$\S 5$习题$5$意义下的纤维(原像).换言之

$$\overline{x}=\lbrace x’\mid f(x’)=f(x)\rbrace .$$

映射$f:X\to Y$诱导出一个映射$\overline{f}:X/\omega _f \to Y$，由法则

$$\overline{f} (\overline{x})=f(x),$$

或

$$\overline{f} p(x)=f(x) \label{2} \tag{2}$$

给出，此处$p$是$\eqref{1}$式中给出的自然映射.由于

$$\overline{x}=\overline{x}’\Leftrightarrow f(x)=f(x’),$$

所以给定$f$，关系式$\eqref{2}$不信赖于类$\overline{x}$中代表元$x$的选取.这时我们说$\overline{f}$的定义是合理的(或良定义的).交换图

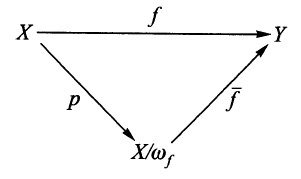
直观地描述了一个分解式

$$f=\overline{f}\cdot p\label{3} \tag{3}$$

映射$f$写成了一个满射$p$与一个单射$\overline{f}$的乘积.$\overline{f}$的单性由下式给出

$$\overline{f}(\overline{x} _1 )=\overline{f}(\overline{x} _2 )\Leftrightarrow f(x _1 )=f(x _2 )\Leftrightarrow \overline{x} _1 =\overline{x} _2 .$$

显然$\overline{f}$的满性等价于$f$的满性.我们指出，如果$f’:X/\omega _f \to Y$是满足条件$\eqref{3}$：$f’\cdot p=f$的另一个映射，则由

$$f’(\overline{x})=f’(p(x))=(f’p)(x)=f(x)=\overline{f}(\overline{x})$$

(见公式$(2)$)得到等式$f’=\overline{f}$.因而上述三角交换图中给出的映射$\overline{f}$是唯一确定的.

序集

一个有序集$X$(或集合$X$上的一个序)指$X$上的一个二元关系$\leq$，满足反身性$(x\leq x)$，反对称性(若$x\leq y$且$y\leq x$，则$x=y$)和传递性(若$x\leq y,y\leq z$，则$x\leq z$).当$x\leq y$且$x\neq y$时，记作$x < y$.$x\leq y$也可以用记号$y\geq x$表示.一对元素$x,x’\in X$可能没有$\leq $关系.但是如果对于$X$的每一对元素都有$x\leq x’$或$x’\leq x$则称$X$为线性序集或全序集.在一般情况下，称$X$上有一个偏序.

给出偏序集的两个例子.集合$S$的子集的集合$\mathcal{P}(S)$(见$\S 5$习题$4$)连同通常的子集之间的包含关系$R\subset T$是一个偏序集.而自然数集$\mathbb{N}$连同关系$d\mid n$($n$被$d$整除)也是一个偏序集.

设$X$是一个偏序集，$x$和$y$是$X$的元素.称$y$紧跟(或覆盖)$x$，如果$x < y$，且不存在元素$z$，使得$x < z < y$.在$\text{Card}X < \infty$的情况下，$x < y$(即$x$与$y$是可比的)当且仅当可以找到一个元素列$x=x_1 ,x_2 ,\cdots ,x_{n-1},x_n =y$，其中$x_{i+1}$紧跟$x_i$.紧跟的概念可以用于绘制有限偏序集的平面图.用点表示集合$X$的元素.若$y$紧跟$x$，则把$y$放在高于$x$的位置上，并将$x$与$y$用直线段连接赶来.$y$与$x$的可比性表现为连接$y$和$x$的一条下降的折线，这样的折线可能同时有几条，$x$与$y$是不可比的则没有折线连接.

在图$10$的前两个图中描述了自然序数的“线段”以及集合$\mathcal{P}(\lbrace a,b,c\rbrace)$($\mathbb{N}$是自然的线性序集，而$\mathcal{P}(S)$的序已在上面给出).

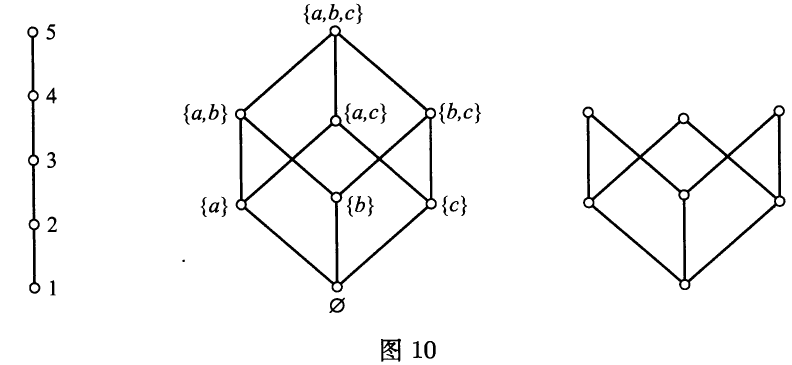
一个偏序集$X$的最大元指元素$n\in X$，使得任取$x\in X$都有$x\leq n$，而极大元指元素$m\in X$，使得从$m\leq x\in X$可得$x=m$.最大元永远是极大的，但反之不真.极大元可以有很多个，但最大元如果存在的话，必定是唯一确定的.相应地可以定义最小元和极小元.在图$10$中，左边的两个图有最大元和最小元，右边的图有三个极大元(一个最小元)，但没有最大元.

偏序代数系统的理论(布尔代数，格论)充满了丰富的结果并在代数学中占有重要地位，但我们不可能去涉及它.本段的目的仅在于使读者认识自然的二元关系并提供图解，它将有助于理解在群当中子群或者域当中子域的相互位置.

习题

$1$.设$\mathbb{R}^2/\sim$是图$8$中给出的商集，$l$是与$OX$轴相交的任意直线，试给出$\mathbb{R}^2/\sim$的元素与$l$的点之间的一一对应.

解：将两点$p,p’\in \mathbb{R}^2 $属于同一条水平直线取作性质$\sim $，它的等价类是水平直线.因此，在$y$轴上任取点$(0,y)$与其等价的所有点的子集为：

$$(\overline{0} ,\overline{y} )=\lbrace (x’,y’)\in \mathbb{R}^2 \mid y’=y\rbrace .$$

于是，$\mathbb{R}^2/\sim$的元素$(\overline{0} ,\overline{y} )$与$l$的点$(x_l ,y_l )$之间的一一对应可定义为$f:(\overline{0} ,\overline{y} )\to (x_l ,y_l )$，其中$\overline{y} =y_l $.

$2$.令实坐标平面$\mathbb{R}^2$上的两点$P(x,y)\sim P(x’,y’)$，当且仅当$x-x’\in \mathbb{Z}$且$y-y’\in \mathbb{Z}$.证明$\sim$是等价关系，且商集可以几何地表示为环面(例如小面包圈的表面，见图$11$)上的点集.

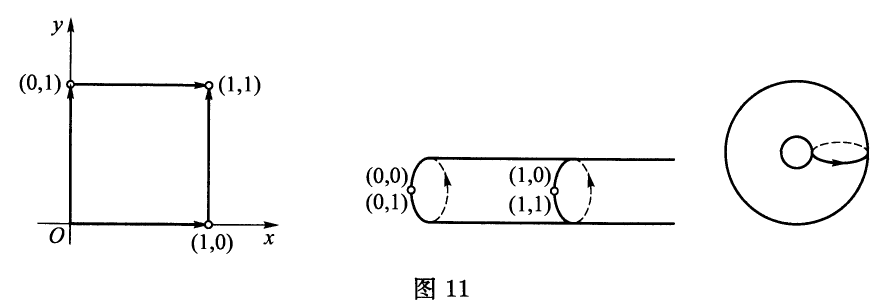
证明：$(1)$平面$\mathbb{R}^2$上的关系$\sim =\lbrace ((x,y),(x’,y’))\mid x-x’\in \mathbb{Z} ,y-y’\in \mathbb{Z} \rbrace \subseteq \mathbb{R}^2 \times \mathbb{R}^2 $.

$a.$点$P(x,y)\sim P(x,y)$，这是因为$x-x\in \mathbb{Z} $且$y-y\in \mathbb{Z} $，故满足反身性；

$b.$若点$P(x,y)\sim P(x’,y’)$，则$x-x’\in \mathbb{Z} $且$y-y’\in \mathbb{Z} $，这时$x’-x\in \mathbb{Z} $且$y’-y\in \mathbb{Z} $，也是满足的，即有$P(x’,y’)\sim P(x,y)$，故满足对称性；

$c.$若$P(x,y)\sim P(x’,y’)$，$P(x’,y’)\sim P(x’’,y’’)$，则$x-x’\in \mathbb{Z} $且$y-y’\in \mathbb{Z} $，同时还有$x’-x’’\in \mathbb{Z} $且$y’-y’’\in \mathbb{Z} $，因此$x-x’’=x-x’+x’-x’’\in \mathbb{Z} $，$y-y’’=y-y’+y’-y’’\in \mathbb{Z} $，即有$P(x,y)\sim P(x’’,y’’)$，故满足传递性.

综合$a,b,c$三点所述，可知$\sim$是平面$\mathbb{R}^2$上的一个等价关系.

相对于等价关系$\sim $而言的商集$\mathbb{R}^2 / \sim $，取$X=[0,1]\times [0,1]$，它们正方形，定义：

$$\begin{align}
X^{\ast } & =\lbrace \lbrace (x,y)\rbrace \mid 0 < x < 1,0 < y < 1 \rbrace \cup \lbrace \lbrace (x,0),(x,1)\rbrace \mid 0 < x < 1 \rbrace \cup \lbrace \lbrace (0,y),(1,y) \rbrace \mid 0 < y < 1\rbrace \\
& \cup \lbrace \lbrace (0,0),(0,1),(1,0),(1,1) \rbrace \rbrace .
\end{align}$$

由$X^{\ast }$所得到的$X$的商空间就是由正方形所得到的橡胶轮胎(环面)，如下图所示.

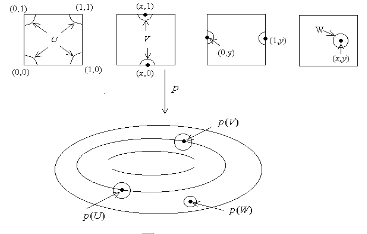
扩展阅读：商拓扑

相似地可推广到任意的区域$P=[x,y]\times [x+n_1 ,y+n_2 ]$，其中$n_1 \in \mathbb{Z} ,n_2 \in \mathbb{Z} $.因此商集可以几何地表示为环面上的点集.

$3$.证明$2$元、$3$元和$4$元集分别有$2$，$5$和$15$个不同的商集.

证明：集合$A$上的等价关系与集合$A$的划分是一一对应的，集合的划分就是把集合分解为几个不相交的非空子集的并集.

因此，对于$1$元集$\lbrace a \rbrace $来说，只有$1$种划分方法：$\lbrace \lbrace a \rbrace \rbrace $；

对于$2$元集$\lbrace a,b \rbrace $来说，有$2$种不同的划分方法：

$$\begin{matrix} \lbrace \lbrace a \rbrace ,\lbrace b \rbrace \rbrace \\ \lbrace \lbrace a,b\rbrace \rbrace .\end{matrix} $$

对于$3$元集$\lbrace a,b,c \rbrace $来说，有$5$种不同的划分方法：

$$\begin{matrix} \lbrace \lbrace a \rbrace ,\lbrace b \rbrace ,\lbrace c \rbrace \rbrace \\ \lbrace \lbrace a\rbrace ,\lbrace b,c \rbrace \rbrace \\ \lbrace \lbrace b \rbrace ,\lbrace a,c \rbrace \rbrace \\ \lbrace \lbrace c \rbrace ,\lbrace a,b \rbrace \rbrace \\ \lbrace \lbrace a,b,c \rbrace \rbrace .\end{matrix} $$

对于$4$元集$\lbrace a,b,c,d \rbrace $来说，有$15$种不同的划分方法：

$$\begin{matrix} \lbrace \lbrace a \rbrace ,\lbrace b \rbrace ,\lbrace c \rbrace ,\lbrace d \rbrace \rbrace \\ \lbrace \lbrace a\rbrace ,\lbrace b,c,d \rbrace \rbrace \\ \lbrace \lbrace b \rbrace ,\lbrace a,c,d \rbrace \rbrace \\ \lbrace \lbrace c \rbrace ,\lbrace a,b,d \rbrace \rbrace \\ \lbrace \lbrace d \rbrace ,\lbrace a,b,c \rbrace \rbrace \\ \lbrace \lbrace a\rbrace ,\lbrace b\rbrace ,\lbrace c,d\rbrace \rbrace \\ \lbrace \lbrace a\rbrace ,\lbrace c\rbrace ,\lbrace b,d\rbrace \rbrace \\ \lbrace \lbrace a\rbrace ,\lbrace d\rbrace ,\lbrace b,c\rbrace \rbrace \\ \lbrace \lbrace b\rbrace ,\lbrace c\rbrace ,\lbrace a,d\rbrace \rbrace \\ \lbrace \lbrace b\rbrace ,\lbrace d\rbrace ,\lbrace a,c\rbrace \rbrace \\ \lbrace \lbrace c\rbrace ,\lbrace d\rbrace ,\lbrace a,b\rbrace \rbrace \\ \lbrace \lbrace a,b\rbrace ,\lbrace c,d\rbrace \rbrace \\ \lbrace \lbrace a,c\rbrace ,\lbrace b,d\rbrace \rbrace \\ \lbrace \lbrace a,d\rbrace ,\lbrace b,c\rbrace \rbrace \\ \lbrace \lbrace a,b,c,d \rbrace \rbrace .\end{matrix} $$

综上所述，$2$元、$3$元和$4$元集分别有$2$，$5$和$15$个不同的商集.

扩展阅读：贝尔数

$4$.设$\sim$是集合$X$上的一个等价关系，且$f:X\to Y$是一个映射，使得

$$x\sim x’ \Rightarrow f(x)=f(x’)$$

证明$f$与$\sim$的这一相容性条件(比第$2$段讨论的条件要弱)允许我们定义一个从$X/\sim$到$Y$的诱导映射$\overline{f}:\overline{x}\mapsto f(x)$，它给出了分解式$f=\overline{f}\cdot p$，但$\overline{f}$不一定是单射.$\overline{f}$成为单射的条件是什么？

证明：设$\sim$是集合$X$上的一个等价关系，其相对应的等价类为：

$$\overline{x}=\lbrace x’\mid f(x’)=f(x)\rbrace .$$

映射$f:X\to Y$诱导出一个映射$\overline{f}:X/\omega _f \to Y$，由法则

$$\overline{f} (\overline{x})=f(x),$$

或

$$\overline{f} p(x)=f(x)\label{4} \tag{4}$$

给出，此处$p$是$\eqref{1}$式中给出的自然映射.由于

$$\overline{x}=\overline{x}’\Leftrightarrow f(x)=f(x’),$$

所以给定$f$，关系式$\eqref{4}$不信赖于类$\overline{x}$中代表元$x$的选取.这时我们说$\overline{f}$的定义是合理的(或良定义的).交换图

直观地描述了一个分解式

$$f=\overline{f}\cdot p,\label{5} \tag{5}$$

但$\overline{f}$不一定是单射的.虽然$\overline{x} _1 =\overline{x} _2 $时，有$f(x _1 )=f(x _2 )$，即$\overline{f}(\overline{x} _1 )=\overline{f}(\overline{x} _2 )$成立.但是当$\overline{f}(\overline{x} _1 )=\overline{f}(\overline{x} _2 )$时，即使有$f(x _1 )=f(x _2 )$，却推导不出$\overline{x} _1 =\overline{x} _2 $.

因此，$f$与$\sim$的这一相容性条件(比第$2$段讨论的条件要弱)允许我们定义一个从$X/\sim$到$Y$的诱导映射$\overline{f}:\overline{x}\mapsto f(x)$，它给出了分解式$f=\overline{f}\cdot p$，但$\overline{f}$不一定是单射.$\overline{f}$成为单射的条件还需要满足$f(x)=f(x’) \Rightarrow x\sim x’ $.

$5$.画出下述偏序集的图解：

$1)\mathcal{P}(\lbrace a,b,c,d\rbrace)$;

$2)$整数$24$的全体因子的集合(偏序关系由整除给出).

解：$(1)\,\mathcal{P}(\lbrace a,b,c,d\rbrace)$偏序集的图解如图所示.

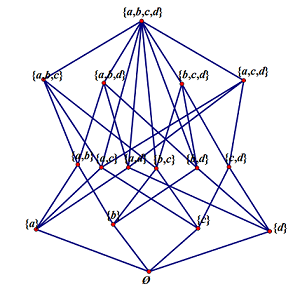
源文件：下载

$(2)$整数$24$的全体因子的集合(偏序关系由整除给出)偏序集的图解如图所示.

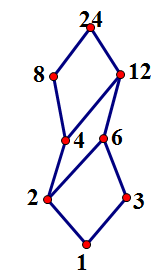
源文件：下载