假设读者对全体自然数(或正整数)的集合$\mathbb{N}=\lbrace 1,2,3,\cdots \rbrace$了解得很清楚.事实上，研究集合$\mathbb{N}$的出发点是皮亚诺公理(皮亚诺，$1858-1932$).从皮亚诺公理可以推导出自然数集，更精确地，非负整数集中加法和乘法的性质以及线性序(见$\S 6$第$4$段).特别是证明了一个直观而清晰的论断：每一个非空集合$S\subset \mathbb{N}$都有最小元，即存在一个自然数$s\in S$它小于$S$中的所有的数.根据皮亚诺公理得到的这一论断推导下述

归纳法原理 假设对每一个$n\in \mathbb{N}$，我们有某一命题$M(n)$.又假设我们有一个法则，对于任意给定的$l$，只要$M(k)$对所有的$k < l$真就可以证明$M(l)$真，特别指出，我们能够验证$M(l)$真.

则对任意的$n\in \mathbb{N}$，$M(n)$真.

事实上，设子集

$$S=\lbrace s\mid s\in \mathbb{N},M(s)不真\rbrace \subset \mathbb{N}$$

不是一个空集.按照上述讨论，$S$包含有一个最小元$s_0$.这时论断$M(s_0 )$不真，而对任意的$s < s_0$，$M(s)$真.这就和我们在假设条件下能够证明$M(s_0 )$真矛盾.

此处我们不能对数学归纳法原理进行全面的讨论.而仅局限于指出它反映了自然数列的本质，对自然数列的认识不能再归结到本质上更简单的事实了.再次将注意力转到归纳法.“完全归纳法证明”必不可少的一步是归纳的基础，即性质或命题对某些不太大的$n$成立.缺少这一验证，就可能推出类似于“所有的学生都一样高”的随意性命题.论证如下.空集和一个学生的集合具有这一性质.给出归纳假设，即任意学生数$\leq n$的集合具有这一性质.则在$(n+1)$个学生的集合中，根据归纳假设，前$n$个学生和后$n$个学生的身高相同.这两个集合有一个有$n-1$个身高相同的学生的子集.因此所有的$n+1$个学生身高相同.事实上，第一步有意义的论断应当对任意两个学生的集合给出，而它恰好是不对的.归纳的基础取多长才够呢？一般来说，这件事从证明中就可以清楚地看出来.在我们这个初等例子中，重要的条件是两个集合的交不空，即不等式$n-1 \geq 1$成立，从而$n \geq 2$.

在更复杂的情况下，特别是当我们借助递推关系用归纳法定义或构造一个对象时，必须对归纳基础格外关心.例如脚标可以被$5$整除的斐波那契数$f_{5m}$(见$\S 3$，例$2$，此处$m \geq 1$)可以由等式$f_5 =5$及递推关系$f_{5(m+1)} =5f_{5m+1} +3f_{5m}$导出，首先得到的是归纳基础.另一方面，也不能陷入另一个极端：对充分长的自然数列$1\leq k\leq l$中的一切$k$验证$M(k)$的正确性，然后作出没有根据的结论，对一切$n\in \mathbb{N} ,M(n)$真(称这一作法为不完全归纳法).

在这里给出两个令人不愉快的例子.

例$1$ 费马猜想，所有形如$F_n =2^{2^n}+1$的费马数都是素数，此处$n=0,1,2,\cdots $.前$5$个费马数是素数.但欧拉找到了$F_5$的一个分解式：$F_5 =4294967297=641\cdot 6700417$.人们执拗地企图在最新式计算机的帮助下找到哪怕一个新的费马素数，但直到现在也没有成功.这一方向的最新“成果”是验证了$F_{1945}$可以被$5\cdot 2^{1947}+1$整除.

例$2$ 观察当$n=1,2,\cdots ,40$时，形如$n^2-n+41$的数(这是欧拉研究的一个多项式)，人们可能会猜想这个多项式对任意$n$都得到素数(关于素数见$\S 9$).但是$41^2-41+41=41^2$.

这种类型的例子要多少有多少.

在用归纳法研究问题时，有时最重要的事情是，使所证的论断具有恰当的形式.假设要求和式

$${\bf p}_k (n)=1^k+2^k+3^k+\cdots +(n-1)^k+n^k,k=1,2,3.$$

如果告诉我们，答案包含在下述表达式中，问题就大大简化了

$${\bf p}_1 (n)=\dfrac{n(n+1)}{2},{\bf p}_2 (n)=\dfrac{n(n+1)(2n+1)}{2},{\bf p}_3 (n)=\left[ \dfrac{n(n+1)}{2} \right] ^2.$$

幂和${\bf p}_k (n)$的一般形式将联系到多项式的根再一次进行讨论(见第$6$章)，此刻我们指出，在$\S 3$第$5$段中遇到的公式$\Gamma (n)$有下述形式

$$\begin{align}
\Gamma (n) & = n(n-1)+\cdots +k(k-1)+\cdots +1(1-1)\\
& = \sum_{k=1}^nk^2-\sum_{k=1}^nk={\bf p}_2 (n)-{\bf p}_1 (n)
\end{align}$$

(今后将会经常用到求和号$\sum$).基于上述${\bf p}_2 (n)$和${\bf p}_1 (n)$的表达式，我们得到$\Gamma (n)=\dfrac{n^3-n}{3}$.显然这一结果可以直接对$\Gamma (n)$作归纳论证得到.

如果说想出${\bf p}_1 (n)$的形式不太困难，那么想出${\bf p}_2 (n)$，${\bf p}_3 (n)$的形式就没那么平凡了，而关系式

$${\bf p}_5 (n)+{\bf p}_7 (n)=2\left( \dfrac{n(n+1)}{2} \right) ^2$$

一般需要按照某种确定的步骤寻找.目前这样的步骤是能够给出的，但我们在这里不考虑它.而证明上述已经给出的对应关系，只需要直接计算从$n$到$n+1$的一步归纳.我们把它留给读者作为有益的练习.

恰好在这一练习中用到下述二项式公式

$$(a+b)^n=a^n+ {n\choose 1} a^{n-1}b+\cdots +{n\choose k} a^{n-k}b^k+\cdots +b^n\label{1}\tag{1}$$

此处$a$和$b$是任意数，而单项式$a^{n-k}b^k$的二项式系数$\LARGE {n\choose k}$形如

$${n\choose k} =\dfrac{n!}{k!(n-k)!}=\dfrac{n(n-1)\cdots (n-k+1)}{k(k-1)\cdots 2\cdot 1},\label{2}\tag{2}$$

这里$n!=n(n-1)\cdots 2\cdot 1$($n$的阶乘).其值快速增长，例如$6!=720$，$10!=3628800$，而$100! > 10^{150}$.对公式$\eqref{2}$进行补充，允许$0!=1$以及当$k < 0$时${\LARGE {n\choose k}}=0$是有益处的.我们还要指出，

$${n\choose n-k}={n\choose k}$$

(二项式系数的对称性).

当$n=1,2$时，公式$\eqref{1}$显然成立，我们对$n$作归纳.假设公式对所有$\leq n$的数成立，用$a+b$去乘$\eqref{1}$式的两端，我们有

$$\begin{align}
(a+b)^{n+1} & =(a+b)^n(a+b)\\
& = a^n(a+b)+\cdots +{n\choose k}a^{n-k}b^k(a+b)+\cdots +b^n(a+b)\\
& = a^{n+1}+a^nb+\cdots +{n\choose k-1}a^{n+2-k}b^{k-1}+{n\choose k-1}a^{n+1-k}b^k\\
& ~ +{n\choose k}a^{n+1-k}b^k+{n\choose k}a^{n-k}b^{k+1}+\cdots +ab^n+b^{n+1}.
\end{align}$$

合并同类项，单项式$a^{n+1-k}b^k$的系数为

$$\begin{align}
& {n\choose k-1}+{n\choose k}\\
& = \dfrac{n!}{(k-1)!(n-k+1)!}+\dfrac{n!}{k!(n-k)!}\\
& = \dfrac{n!}{(k-1)!(n-k)!}\left[ \dfrac{1}{n-k+1}+\dfrac{1}{k} \right] \\
& = \dfrac{n!}{(k-1)!(n-k)!}\cdot \dfrac{n+1}{k(n-k+1)}\\
& = \dfrac{(n+1)!}{k!(n+1-k)!}\\
& = {n+1\choose k}
\end{align}$$

即恰好对形如$\eqref{2}$的二项式系数的上指标增加$1$.这就证明了公式对一切$n\in \mathbb{N}$成立.

如果写成

$$(a+b)^n=(a+b)(a+b)\cdots (a+b),$$

给右边的因子从$1$到$n$编号，并考察所有的编号为

$$1 \leq i_1 < i_2 < \cdots < i_k \leq n$$

的子集，它们与乘积中的单项式$a^{n-k}b^k$相符，所以我们断言，$\LARGE {n\choose k}$恰为$n$元集中所有$k$元子集的个数.比较老式的术语是从$n$个元素中每次取$k$个元素的组合数

$$C_n^k={n\choose k},$$

这是一种本质上的表述.

特别地，集合$\mathcal{P}(\lbrace s_1 ,\cdots ,s_n \rbrace )$(见$\S 5$习题$4$)的基数等于

$${n\choose 0}+{n\choose 1}+\cdots +{n\choose n-1}+{n\choose n}.$$

在公式$\eqref{1}$中令$a=b=1$，我们得到

$$2^n={n\choose 0}+{n\choose 1}+\cdots +{n\choose n-1}+{n\choose n}.$$

于是，

$$\text{Card}\mathcal{P}(\lbrace s_1 ,\cdots ,s_n \rbrace )=2^n.$$

二项式系数在初等组合论中几乎是必不可少的.下面是一个直观的几何例子.

例(美国数学月刊，$\text{1977,V.84,No.6}$)给定圆周上任意$n$个点，确定由$\LARGE {n\choose 2}$条弦划分的圆内的区域数$R_n$.此处假设任意三条弦在圆内不相交(见图$12$).这是一个著名的问题.

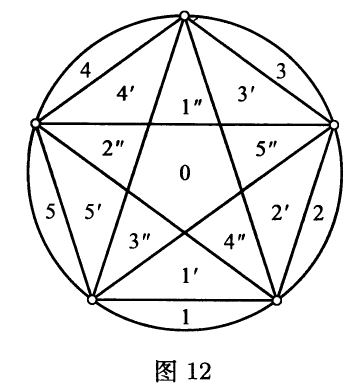
当$n=1,2,3,4,5$时的结果使人们想到$R_n =2^{n-1}$，但事实上，正确的公式为$R_n =1+{\LARGE {n\choose 2}}+{\LARGE {n\choose 4}}$.试证明之.

证明定理或构造数学对象时，有时需要借助更复杂的归纳形式.例如下面的二重归纳原理.设任取自然数$m$和$n$，有某一命题$Y(m,n)$，并且：

$i)~Y(m,1)$和$Y(1,n)$对所有的$m,n$真；

$ii)$如果$Y(k-1,l)$和$Y(k,l-1)$真，则$Y(k,l)$亦真.

(这就等价于说：

$ii’)$如果对一切满足$k’ \leq k$，$l’ \leq l$，$k’+l’ < k+l$的数对$(k’,l’)$，$Y(k’,l’)$真，则$Y(k,l)$亦真.)

那么命题$Y(m,n)$对所有的自然数$m$和$n$都真.

习题

$1$.令

$$s(n)=\sin{\varphi }+\sin{2\varphi }+\cdots +\sin{n\varphi },$$

$$c(n)=\cos{\varphi }+\cos{2\varphi }+\cdots +\cos{n\varphi }.$$

对$n$作归纳证明公式

$$s(n)=\dfrac{\sin{(n\varphi /2)} \sin{((n+1)\varphi /2)}}{\sin{(\varphi /2)}},c(n)=\dfrac{\sin{(n\varphi /2)} \cos{((n+1)\varphi /2)}}{\sin{(\varphi /2)}}.$$

证明：$(1)$.对$n$作归纳证明公式

$$s(n)=\dfrac{\sin{\dfrac{n\varphi }{2}} \sin{\dfrac{(n+1)\varphi }{2}}}{\sin{\dfrac{\varphi }{2}}}.$$

当$n=1$时，$s(1)=\sin{\varphi } =\dfrac{\sin{\dfrac{1\cdot \varphi }{2}} \sin{\dfrac{(1+1)\varphi }{2}}}{\sin{\dfrac{\varphi }{2}}}$，公式$s(n)$对于$n=1$时成立.

现在假设公式$s(n)$对于$n-1$时也成立,即

$$s(n-1)=\dfrac{\sin{\dfrac{(n-1)\varphi }{2}} \sin{\dfrac{n\varphi }{2}}}{\sin{\dfrac{\varphi }{2}}}.$$

那么，

$$\begin{align}
& \sin{\varphi }+\sin{2\varphi }+\cdots +\sin{n\varphi } \\
= & \sin{\varphi }+\sin{2\varphi }+\cdots +\sin{(n-1)\varphi } +\sin{n\varphi } \\
= & \dfrac{\sin{\dfrac{(n-1)\varphi }{2}} \sin{\dfrac{n\varphi }{2}}}{\sin{\dfrac{\varphi }{2}}} +\sin{n\varphi } \\
= & \dfrac{\sin{\dfrac{(n-1)\varphi }{2}} \sin{\dfrac{n\varphi }{2}} +\sin{n\varphi } \sin{\dfrac{\varphi }{2}} }{\sin{\dfrac{\varphi }{2}}} \\
= & \dfrac{\sin{\dfrac{(n-1)\varphi }{2}} \sin{\dfrac{n\varphi }{2}} +2\sin{\dfrac{n\varphi }{2}} \cos{\dfrac{n\varphi }{2}}\sin{\dfrac{\varphi }{2}} }{\sin{\dfrac{\varphi }{2}}} \\
= & \dfrac{\sin{\dfrac{n\varphi }{2}} \left( \sin{\dfrac{(n-1)\varphi }{2}} +2\cos{\dfrac{n\varphi }{2}}\sin{\dfrac{\varphi }{2}} \right) }{\sin{\dfrac{\varphi }{2}}} \\
= & \dfrac{\sin{\dfrac{n\varphi }{2}} \left( \sin{\left( \dfrac{n\varphi }{2}-\dfrac{\varphi }{2} \right) } +2\cos{\dfrac{n\varphi }{2}}\sin{\dfrac{\varphi }{2}} \right) }{\sin{\dfrac{\varphi }{2}}} \\
= & \dfrac{\sin{\dfrac{n\varphi }{2}} \left( \sin{\dfrac{n\varphi }{2} } \cos{\dfrac{\varphi }{2} }-\cos{\dfrac{n\varphi }{2} } \sin{\dfrac{\varphi }{2} }+2\cos{\dfrac{n\varphi }{2}}\sin{\dfrac{\varphi }{2}} \right) }{\sin{\dfrac{\varphi }{2}}} \\
= & \dfrac{\sin{\dfrac{n\varphi }{2}} \left( \sin{\dfrac{n\varphi }{2} } \cos{\dfrac{\varphi }{2} }+\cos{\dfrac{n\varphi }{2} } \sin{\dfrac{\varphi }{2} } \right) }{\sin{\dfrac{\varphi }{2}}} \\
= & \dfrac{\sin{\dfrac{n\varphi }{2}} \sin{\left( \dfrac{n\varphi }{2} +\dfrac{\varphi }{2} \right) } }{\sin{\dfrac{\varphi }{2}}} \\
= & \dfrac{\sin{\dfrac{n\varphi }{2}} \sin{ \dfrac{(n+1)\varphi }{2} } }{\sin{\dfrac{\varphi }{2}}} ,\\
\end{align}$$

公式$s(n)$对于$n$也是成立的.因此根据归纳法，公式$s(n)$对一切正整数$n$都成立.

$(2)$.同理，对$n$作归纳证明公式

$$c(n)=\dfrac{\sin{\dfrac{n\varphi }{2}} \cos{\dfrac{(n+1)\varphi }{2}}}{\sin{\dfrac{\varphi }{2}}}.$$

当$n=1$时，$c(1)=\cos{\varphi } =\dfrac{\sin{\dfrac{1\cdot \varphi }{2}} \cos{\dfrac{(1+1)\varphi }{2}}}{\sin{\dfrac{\varphi }{2}}}$，公式$c(n)$对于$n=1$时成立.

现在假设公式$c(n)$对于$n-1$时也成立,即

$$c(n-1)=\dfrac{\sin{\dfrac{(n-1)\varphi }{2}} \cos{\dfrac{n\varphi }{2}}}{\sin{\dfrac{\varphi }{2}}}.$$

那么，

$$\begin{align}
& \cos{\varphi }+\cos{2\varphi }+\cdots +\cos{n\varphi } \\
= & \cos{\varphi }+\cos{2\varphi }+\cdots +\cos{(n-1)\varphi } +\cos{n\varphi } \\
= & \dfrac{\sin{\dfrac{(n-1)\varphi }{2}} \cos{\dfrac{n\varphi }{2}}}{\sin{\dfrac{\varphi }{2}}} +\cos{n\varphi } \\
= & \dfrac{\sin{\dfrac{(n-1)\varphi }{2}} \cos{\dfrac{n\varphi }{2}} +\cos{n\varphi } \sin{\dfrac{\varphi }{2}} }{\sin{\dfrac{\varphi }{2}}} \\
= & \dfrac{\sin{\left( \dfrac{n\varphi }{2} -\dfrac{\varphi }{2} \right) } \cos{\dfrac{n\varphi }{2}} +\cos{\left( \dfrac{n\varphi }{2} +\dfrac{n\varphi }{2} \right) } \sin{\dfrac{\varphi }{2}} }{\sin{\dfrac{\varphi }{2}}} \\
= & \dfrac{\left( \sin{\dfrac{n\varphi }{2} } \cos{\dfrac{\varphi }{2} } -\cos{\dfrac{n\varphi }{2} } \sin{\dfrac{\varphi }{2} }\right) \cos{\dfrac{n\varphi }{2}} +\left( \cos{\dfrac{n\varphi }{2} } \cos{\dfrac{n\varphi }{2} } -\sin{\dfrac{n\varphi }{2} } \sin{\dfrac{n\varphi }{2} } \right) \sin{\dfrac{\varphi }{2}} }{\sin{\dfrac{\varphi }{2}}} \\
= & \dfrac{\sin{\dfrac{n\varphi }{2} } \cos{\dfrac{\varphi }{2} } \cos{\dfrac{n\varphi }{2}} -\cos{\dfrac{n\varphi }{2} } \sin{\dfrac{\varphi }{2} }\cos{\dfrac{n\varphi }{2}} +\cos{\dfrac{n\varphi }{2} } \cos{\dfrac{n\varphi }{2} } \sin{\dfrac{\varphi }{2}} -\sin{\dfrac{n\varphi }{2} } \sin{\dfrac{n\varphi }{2} } \sin{\dfrac{\varphi }{2}} }{\sin{\dfrac{\varphi }{2}}} \\
= & \dfrac{\sin{\dfrac{n\varphi }{2} } \cos{\dfrac{\varphi }{2} } \cos{\dfrac{n\varphi }{2}} -\sin{\dfrac{n\varphi }{2} } \sin{\dfrac{n\varphi }{2} } \sin{\dfrac{\varphi }{2}} }{\sin{\dfrac{\varphi }{2}}} \\
= & \dfrac{\sin{\dfrac{n\varphi }{2} } \left( \cos{\dfrac{\varphi }{2} } \cos{\dfrac{n\varphi }{2}} -\sin{\dfrac{n\varphi }{2} } \sin{\dfrac{\varphi }{2}} \right) }{\sin{\dfrac{\varphi }{2}}} \\
= & \dfrac{\sin{\dfrac{n\varphi }{2} } \cos{\left( \dfrac{\varphi }{2} +\dfrac{n\varphi }{2} \right) } }{\sin{\dfrac{\varphi }{2}}} \\
= & \dfrac{\sin{\dfrac{n\varphi }{2} } \cos{\dfrac{(n+1)\varphi }{2} } }{\sin{\dfrac{\varphi }{2}}} ,\\
\end{align}$$

公式$c(n)$对于$n$也是成立的.因此根据归纳法，公式$c(n)$对一切正整数$n$都成立.

$2$.下述公式成立：

$a)\, \displaystyle \sum_{k=1}^{n}\cot{}^2(\dfrac{k\pi}{2n+1})=\dfrac{n(2n-1)}{3}$;

$b)\, \displaystyle \sum_{k=0}^{n}{2k\choose n}{2n-2k\choose n-k}=4^n$.

至少在$n\leq 5$时，验证它们的正确性.

证明：$a)$.由棣莫弗公式可知，

$$\begin{align}
& \cos{m\theta } +i\sin{m\theta } \\
= & (\cos{\theta }+i\sin{\theta })^m \\
= & \sin{}^m \theta (\cot{\theta } +i)^m \\
= & \displaystyle \sin{}^m \theta \sum_{k=0}^m {m\choose k} i^k \cot{}^{m-k} \theta ,
\end{align}$$

我们就得到三角恒等式

$$\sin{m\theta } =\sin{}^m \theta \left\lbrace {m\choose 1} \cot{}^{m-1} \theta -{m\choose 3} \cot{}^{m-3} \theta +{m\choose 5} \cot{}^{m-5} \theta - +\cdots \right\rbrace .$$

取$m=2n+1$，代入上式得到

$$\sin{(2n+1)\theta } =\sin{}^{2n+1} \theta P_n (\cot{}^2 \theta ) ,0 < \theta < \dfrac{\pi }{2} ,\label{3} \tag{3}$$

$P_n$是由下列式子给出的$n$维多项式：

$$P_n (x) =\binom{2n+1}{1} x^n -\binom{2n+1}{3} x^{n-1} +\binom{2n+1}{5} x^{n-2}- +\cdots .$$

因为$0 < \theta < \dfrac{\pi }{2} $，故$\sin{\theta } \neq 0$.对于某些整数$k$来说，如果$(2n+1)\theta =k\pi $，方程$\eqref{3}$表明$P_n (\cot{}^2 \theta )=0$.所以在$n$个不同点$x_k =\cot{}^2 \dfrac{\pi k}{2n+1} $，$k=1,2,\cdots ,n$中$P_n (x)$为零.这些$P_n (x)$的零点的和为：

$$\displaystyle \sum_{k=1}^n \cot{}^2 \dfrac{k\pi }{2n+1} =\dfrac{\binom{2n+1}{3} }{\binom{2n+1}{1} } =\dfrac{n(2n-1)}{3}.$$

$b)$.考察式子$r(r-\dfrac12 )(r-1)(r-\dfrac32 )\cdots (r-k+1)(r-k+\dfrac12)$，其中$r$是任意的实数.

因为

$$\begin{align}
& r(r-\dfrac12 )(r-1)(r-\dfrac32 )\cdots (r-k+1)(r-k+\dfrac12) \\
= & \dfrac{2r}{2} \dfrac{2r-1}{2} \dfrac{2r-2}{2} \dfrac{2r-3}{2} \cdots \dfrac{2r-2k+2}{2} \dfrac{2r-2k+1}{2} \\
= & \dfrac{(2r)(2r-1)(2r-2)(2r-3)\cdots (2r-2k+2)(2r-2k+1)}{\underbrace{2\cdot 2\cdot 2\cdot 2\cdots 2\cdot 2}_{2k~个~2}}
\end{align}$$

等价于：

$$\begin{align}
& r(r-1)\cdots (r-k+1) (r-\dfrac12 )(r-\dfrac32 )\cdots (r-k+\dfrac12) \\
= & \dfrac{(2r)(2r-1)(2r-2)(2r-3)\cdots (2r-2k+2)(2r-2k+1)}{2^{2k}} \\
\end{align}$$

等式的左边乘以$1=\dfrac{(r-k)(r-k-1)\cdots 2\cdot 1}{(r-k)(r-k-1)\cdots 2\cdot 1} \cdot \dfrac{(r-\dfrac{2k+1}{2})(r-\dfrac{2k+3}{2})\cdots 2\cdot 1}{(r-\dfrac{2k+1}{2})(r-\dfrac{2k+3}{2})\cdots 2\cdot 1}$，得：

$$\begin{align}
& r(r-1)\cdots (r-k+1) (r-\dfrac12 )(r-\dfrac32 )\cdots (r-k+\dfrac12) \\
= & \dfrac{r(r-1)\cdots (r-k+1)\cdot (r-k)(r-k-1)\cdots 2\cdot 1 }{(r-k)(r-k-1)\cdots 2\cdot 1} \\
& \cdot \dfrac{(r-\dfrac12 )(r-\dfrac32 )\cdots (r-k+\dfrac12) \cdot (r-\dfrac{2k+1}{2})(r-\dfrac{2k+3}{2})\cdots 2\cdot 1 }{(r-\dfrac{2k+1}{2})(r-\dfrac{2k+3}{2})\cdots 2\cdot 1} \\
= & \dfrac{r!}{(r-k)!} \cdot \dfrac{( r-\dfrac12 ) !}{( r-\dfrac{1}{2} -k ) !}
\end{align}$$

等式的右边乘以$1=\dfrac{(2r-2k)(2r-2k-1)\cdots 2\cdot 1}{(2r-2k)(2r-2k-1)\cdots 2\cdot 1} \cdot \dfrac{(2k)!}{(2k)!}$，得

$$\begin{align}
& \dfrac{(2r)(2r-1)(2r-2)(2r-3)\cdots (2r-2k+2)(2r-2k+1)}{2^{2k}} \\
= & \dfrac{(2r)(2r-1)\cdots (2r-2k+1)\cdot (2r-2k)(2r-2k-1)\cdots 2\cdot 1 \cdot (2k)!}{(2r-2k)(2r-2k-1)\cdots 2\cdot 1 \cdot (2k)! \cdot 2^{2k}} \\
= & \dfrac{(2r)!}{(2r-2k)!\cdot (2k)! } \cdot \dfrac{(2k)!}{2^{2k}} \\
\end{align}$$

因为等式的左边等于右边，所以有

$$\dfrac{r!}{(r-k)!} \cdot \dfrac{( r-\dfrac12 ) !}{( r-\dfrac{1}{2} -k ) !} =\dfrac{(2r)!}{(2r-2k)!\cdot (2k)! } \cdot \dfrac{(2k)!}{2^{2k}}$$

这时等式两边可同时除以$k!\cdot k!$，得到

$$\dfrac{r!}{(r-k)!\cdot k!} \cdot \dfrac{( r-\dfrac12 ) !}{( r-\dfrac{1}{2} -k ) !\cdot k!} =\dfrac{(2r)!}{(2r-2k)!\cdot (2k)! } \cdot \dfrac{(2k)!}{k!\cdot k!} \cdot \dfrac{1}{2^{2k}}$$

$$\binom{r}{k} \cdot \binom{r-\dfrac12 }{k} =\binom{2r}{2k} \cdot \binom{2k}{k} \cdot \dfrac{1}{2^{2k}},$$

其中$k$为整数.令$n=k=r$代入上式，得到

$$\binom{n-\dfrac12 }{n} =\binom{2n}{n} \cdot \dfrac{1}{2^{2n}},$$

其中$n$为整数.

所以有

$$\binom{-\dfrac12 }{n} =\left( \dfrac{-1}{4} \right) ^n \cdot \binom{2n}{n} .$$

利用上面的推论考察式子$\displaystyle \sum_{k=0}^n \binom{-\dfrac12 }{k} \binom{-\dfrac12 }{n-k} $.

首先利用公式$\displaystyle \sum_{k=0}^n \binom{r}{k} \binom{s}{n-k} =\binom{r+s}{n} $，其中$n$为整数，得到

$$\displaystyle \sum_{k=0}^n \binom{-\dfrac12 }{k} \binom{-\dfrac12 }{n-k} =\binom{-1}{n} =(-1)^n,$$

其中$n$为整数.而另一方面，

$$\binom{-\dfrac12 }{k} \binom{-\dfrac12 }{n-k} =\left( \dfrac{-1}{4} \right) ^k \cdot \binom{2k}{k} \cdot \left( \dfrac{-1}{4} \right) ^{n-k} \cdot \binom{2(n-k)}{n-k} =\dfrac{(-1)^n}{4^n} \cdot \binom{2k}{k} \cdot \binom{2(n-k)}{n-k},$$

于是有

$$\displaystyle \sum_{k=0}^n \binom{-\dfrac12 }{k} \binom{-\dfrac12 }{n-k} =\sum_{k=0}^n \dfrac{(-1)^n}{4^n} \cdot \binom{2k}{k} \cdot \binom{2(n-k)}{n-k}=(-1)^n,$$

整理得

$$\displaystyle \sum_{k=0}^n \binom{2k}{k} \cdot \binom{2(n-k)}{n-k}= 4^n.$$

综上所述，公式$a,b$至少在$n\leq 5$时，都是成立的.