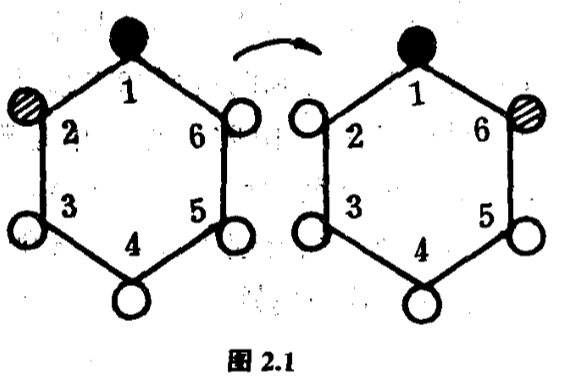
让我们先从第一章第$1.1$节的问题着手，看看是什么性质使那三道问题的答案不相同.首先，如果那六个端点是可区别的话，则不论它们是正六边形的端点，或是正八面体的端点、或是三棱柱的端点，放置彩色球的摆法个数都是$30$个.所以，首先要解释为什么那六个端点是不可区别的，看一个例子吧.把正六边形放在一个固定不动同样大小的正六边形盘子上，盘子的六个角各标以$1$号至$6$号.把黑球嵌在$1$号的端点，红球嵌在$2$号的端点、白球嵌在$3$号、$4$号、$5$号和$6$号的端点.现在把放置了球的构形绕着联结$1$号端点和$4$号端点的直线作轴翻转$180^{\circ } $，再放回盘子上.得到的构形变成黑球嵌在$1$号的端点、红球嵌在$6$号的端点、白球嵌在$2$号、$3$号、$4$号和$5$号的端点（图$2.1$）.在$30$种摆法中，这两种摆法是不相同的，但作为构形，它们却是相同的.就这个意义说，那六个端点是不可区别的.

读者可以意会到某些移动对这类问题起了关键作用，我指的是那些不变更一个给定的几何形体的位置的移动，虽然每点的位置却可能给调换了.例如对一个正六边形来说，绕着中心转$0^{\circ } $、$60^{\circ } $、$120^{\circ } $、$180^{\circ } $、$240^{\circ } $、$300^{\circ } $，或者绕着一条联结对角点的直线作轴翻转$180^{\circ } $，或者绕着一条联结对边中点的直线作轴翻转$180^{\circ } $，这$12$个移动都不变更六边形的位置.我们把这种移动叫做那个几何形体的对称，在下一节读者便会明白为什么把这种移动叫作对称，请读者暂时接受以下的事实：正六边形的全部对称就是刚才举出的$12$个，但正八面体有较多对称，共有$24$个，而三棱柱体却只有$6$个对称.既然三道问题涉及的几何形体具有不同的对称，而对称又直接影响问题的答案，那么三道问题的答案不相同，也就不足为怪了.

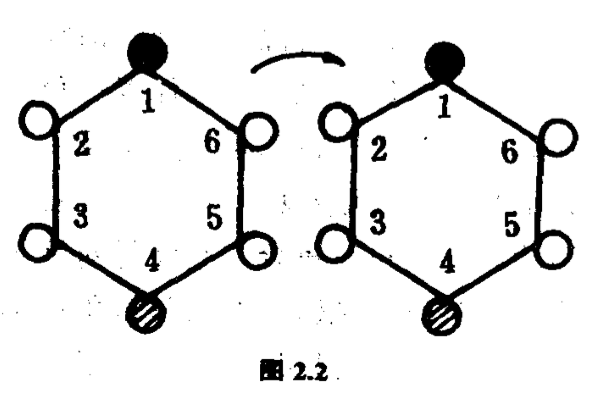
在下一节我们将集中讨论对称，然后在第三章第$3.4$节讨论如何运用对称的知识去解决构形计数的问题.不妨先在这儿提出一点值得留意的事情，就是不同的对称可不一定导致不同的摆法.例如在刚才的例子里，把黑球嵌在$1$号的端点、红球嵌在$4$号的端点、白球嵌在$2$号、$3$号、$5$号和$6$号的端点，绕着联结$1$号端点和$4$号端点的直线作轴翻转$180^{\circ}$，再放回盘子上，得到的构形和未移动前的构形，摆法仍然是相同的（图$2.2$）.由此可见，单是数摆法固然不一定获得正确的答案，单是数对称也不一定获得正确的答案.我们必须捉住二者的关联，结合起来计算，才能获得正确的答案，读者在第三章便看到其中的奥妙了！