读者一定寄过信吧？信抵邮局，按种类大小给划分.让我们只考虑普通信件，它们每封的形状大小差不多，叠齐了职员便盖邮戳.但虽然叠齐了，信封上贴邮票的角落（正面右上角）却不一定都落在同一个位置，在一叠信件里，邮票可能落在四个位置，分别记作$(1)$、$(2)$、$(3)$和$(4)$，如图$2.3$所示.

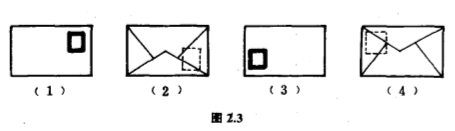
为了省钱，探测邮票的感应器是固定的，它只探测信封的正面右上角.现在问：应该怎样把信移动，务使$(1)$、$(2)$、$(3)$和$(4)$这四种情况都受到处理，在邮票上盖上邮戳呢？当然，我们可以先探测正面右上角，有邮票的话便划分开来盖邮戳，没有的话便把信绕着一条横中线作轴翻转$180^{\circ }$（把这个移动叫做$H$），然后探测；有邮票的话便划分开来盖邮戳，没有的话便再用一次$H$这个移动还原；按着把信绕着中心旋转$180^{\circ}$（把这个移动叫做$R$），然后探测；有邮票的话便划分开来盖邮戳，没有的话便再用一次$R$这个移动还原；接着把信绕着一条纵中线作轴翻转$180^{\circ}$（把这个移动叫做$V$），然后探测；如果还探测不到邮票，那么只有两种可能，或者发信人没有贴邮票，或者他把邮票贴在错误的位置上，无论是哪一种情况，划分开来处理便是（图$2.4$）.

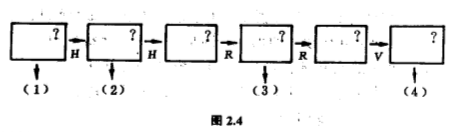
这样做最多可要用遍五次移动，但其实先用$H$再用$R$，效果等于只用一次$V$；同样地，先用$R$再用$V$，效果等于只用一次$H$.换句话说，刚才一连串五个移动，可以缩减为三个：探测，然后用$H$，再探测，然后用$V$，再探测，然后用$H$，最后探测（图$2.5$）.

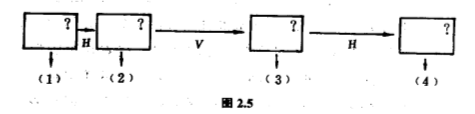
除了减少步骤外，这样做还可以避免采用某些较难实施的移动.例如第二种方案只有三步，而且没有一步用$R$，$R$比$H$或$V$较难实施，有些邮局的自动排信机，的确是采用这种方案的.

转看另一个应用的例子，是电脑的循环式储存器的存取控制.为了简化叙述，假定只有四个储存器，循环地转动，要取得储存于某个储存器的资料，必须待它旋转抵达阅读站是方能把它取出来抄写.为了记录哪一个储存器转抵阅读站，有个计数器负责记录工作，比如开始时$0$号储存器在阅读站，计数器出现$0$，以后每转一次，计数器即加$1$.所以当$1$号储存器抵阅读站时，计数器出现$1$；$2$号储存器抵阅读站时，计数器出现$2$.但这样加下去，转$4$次后计数器岂不是出现$4$，转$5$次后计数器岂不是出现$5$吗？然而抵达阅读站的储存器却分别是$0$号和$1$号呀！因此，计数器使用的加法，不是普通的加法，而是一种数学上称作模$4$的加法，即是按普通加法得出的和，以$4$除和，剩下的余数才是答案.例如模$4$的加法中，$2+3=1$，因为$2+3$本来是$5$，以$4$除$5$余$1$，这也表示了转$2$次接着转$3$次，效果等于只转$1$次.

上面两个应用的例子与第$2.2$节的对称有什么关系呢？在第一个例子里，这个关系是明显不过，我们面对的根本就是一个矩形（非正方形）的对称，共有$4$个，即是上面叫做$H$、$R$、$V$那三个移动和纹丝不动的这一个移动，让我们把最后一个移动叫做$I$.第二个例子其实也可以看做是某个几何图形的对称，比如说梵文万字的对称（图$2.6$）.

绕着这个图形的四次对称心转$0^{\circ}$、$90^{\circ}$、$180^{\circ}$、$270^{\circ}$，得到$4$个对称，也就是全部对称了.请读者注意，镜像反影（相当于把图形翻转）并不是这个图形的对称，它把梵文万字变成另一个意义完全不同的丑恶符号！（说来也巧，原来的梵文万字是图中所见的图形的镜像，它在不少古代文化里都曾出现，是吉祥仁慈的标记.在$1920$年希特勒采用了这个符号作为他的国社党——简称纳粹党——的党徽，从此这符号便给玷污了.但这个符号随佛教传入古代中国时，不知怎的却被翻转了，一直误传下去，竟又与纳粹党徽有别！）

虽然矩形和梵文万字都有四个对称，直觉上我们意会到二者的对称性质有别.比如矩形拥有两条对称轴，也即是说相应于这两条对称轴的对称重复一次便把图形还原；剩下的两个对称，一个是恒定不动，另一个是绕二次对称心转$180^{\circ}$，后者重复一次也把图形还原.梵文万字却没有对称轴，只有绕四次对称心转$180^{\circ}$这个对称重复一次把图形还原，剩下的三个对称，一个是恒定不动，另外两个都是重复至少三次才把图形还原.因此，要注意的不单是有多少个对称，还得注意这些对称之间的结合关系.所谓结合关系，就是指先实施移动甲再实施移动乙，效果是否等于只实施某一个移动呢？是的话又是哪一个移动呢？最清晰的表达方式是列一个结合关系表，全部对称以符号代替，放置在第一行第一列，在每行每列相交的位置写下位于该行该列的对称的结合.例如第一个例子里的四个对称的结合关系表，如图$2.7$所示.

看看$R$那一行和$V$那一列，相交的位置出现$H$，意思是说先实施$V$再实施$R$，效果等于只实施$H$，简写作$RV=H$.第二个例子里的四个移动，看成是梵文万字的对称，以$e$、$r$、$s$、$t$代替，分别是绕着四次对称心转$0^{\circ}$、$90^{\circ}$、$180^{\circ}$、$270^{\circ}$，得出来的结合关系表，如图$2.8(a)$所示.

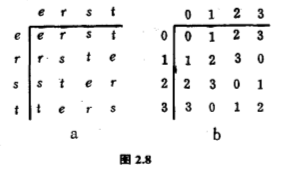
请读者留意，这个表和$0$、$1$、$2$、$3$的模$4$加法表（图$2.8(b)$）是不是很相似呢？只要把$e$、$r$、$s$、$t$分别换作$0$、$1$、$2$、$3$，便从一个表得出另一个表了.但这个表跟前一个表（图$2.7$）却有本质上的差别，无论你怎样调换$e$、$r$、$s$、$t$的次序，再易名为$I$、$R$、$V$、$H$，也绝对没有办法得出前一个表的，其中道理我们刚才解释过.