设$G$是个群，它的单位元$e$的界定性质是：对任意$G$中元$a$，有$ae=ea=a$.由此不难证明单位元是唯一的，如果元$e’$也满足同样性质，便有$e’e=e’$和$e’e=e$，所以$e’=e$.对$a$来说，它的逆元$a’$的界定性质是：$aa’=a’a=e$.由此也不难证明$a$的逆元是唯一的，如果元$a’’$也满足同样性质，便有$a’’=a’’e=a’’(aa’)=(a’’a)a’=ea’=a’$.通常我们把$a$的逆元记作$a^{-1}$.由于存在逆元，群$G$满足消去律，即是说：如果$ab=ac$，则$b=c$；如果$ba=ca$，则$b=c$.这是因为从$ab=ac$可得$a^{-1}(ab)=a^{-1}(ac)$，从而$(a^{-1}a)b=(a^{-1}a)c$，即$eb=ec$，亦即$b=c$；同理，从$ba=ca$可得$b=c$.以上所述，其实都是读者自小学中学以来便耳熟能详的知识，在四则运算中经常用了而不自觉，只是当时并非从这种角度看待问题吧.比方说，解方程$2x+3=7$，未知数$x$代表某些暂时不知道真正数值的实数.它既代表某些实数，适用于一般实数的四则运算也就可施诸于它们的身上了.我们把方程改写成$2x=4$，那就是考虑实数以加法结合的群，对两边的元同时加上$3$的逆元$-3$，再化简.接着我们把方程改写成$x=2$，那就是考虑非零实数以乘法结合的群，对两边的元同时乘上$2$的逆元$1/2$，再化简，由此得出答案.

不过，群这个概念自然不局限于实数的四则运算，它包罗众多数学对象.读者将会在下面的章节里碰到越来越多群的例子，现在让我们看看一些简单的群的基本性质.

请看第$2.4$节结尾提及的群，从群表（图$2.9$）中读者是否留意到它蕴藏了一个较小的四元群在里面呢？那就是由$e$、$r$、$s$、$t$组成的子集，其实它是一个与梵文万字对称群有相同结构的群，它对应的是绕着中心转$0^{\circ}$、$90^{\circ}$、$180^{\circ}$、$270^{\circ}$的对称.我们说它是原来那个群的子群，意思是说按原来的群的结合关系，它自身仍然是一个群.例如在实数加群$R$里（即是全部实数以加法结合的群），全部整数组成一个子群$Z$，但全部正数却不组成一个子群，比如说它没有单位元（它的单位元只好是$0$，但$0$并不是一个正数）.不过要注意一点，虽然群$G$里的一个子集并不一定是子群，对别的结合关系来说，它可能是个群，只是它的结合关系跟原来的群没有直属关系，我们不把它叫做原来群的子群罢了.例如刚刚提到的正数集$P$虽然不是实数加群$R$里的子群，但对乘法来说它是一个群.（有兴趣的读者不妨考虑以下的问题：正数乘群$P$、非零实数乘群$R^{\ast }$、实数加群$R$、整数加群$Z$，全部都是无限群，它们的结构是否相同呢？哪些跟哪些的结构相同呢？）

怎样验证群$G$里的一个子集$H$是不是子群？首先，$H$必须是非空集；其次，如果$a$和$b$是$H$中元，它们的乘积$ab$必须也落在$H$里；还有，如果$a$是$H$中元，它的逆元$a^{-1}$也必须落在$H$里.反过来说，这些条件已足够保证$H$是$G$的子群.读者会问：“单位元在$H$吗？结合律成立吗？”$H$是$G$是一部分，既然结合律在$G$成立，它自然在$H$也成立.$H$是非空集，它必有至少一个元$a$，所以它也拥有$a^{-1}$，因而它也拥有$aa^{-1}=e$了.当$H$是非空的有限集时，我们甚至只要验证一个条件：当$a$和$b$是$H$中元时，它们的乘积$ab$也是$H$中元.读者愿意试试自行证明这一回事吗？让我给你一个提示，选定$H$中一个元$a$，把它遍乘全部$H$中元，看看得到一个什么样的集合.

研究群的结构往往从它的子群着手，在某种意义下，子群较原来的群简单，有时某些子群与原来的群关系密切，以致凭着这些子群的资料我们能获悉全部或者至少大部分原来的群的情况.举一个十分简单的例子，矩形（非正方形）的对称群$\lbrace I,R,V,H\rbrace $有三个二元子群，就是$\lbrace I,R\rbrace $、$\lbrace I,V\rbrace $和$\lbrace I,H\rbrace $其中任何两个已足以刻画整个群，因为那个群的任意元能唯一地写作两个分别落在每一个子群的元的乘积.试取$\lbrace I,R\rbrace $和$\lbrace I,V\rbrace $，则$H=RV$.看看梵文万字的对称群，它只有一个二元子群，就是$\lbrace e,s\rbrace $，凭着它我们不能像上述一般刻画整个群.但如果我们取$r$（或$t$）生成的子群，即是尽取一切由$r$（或$t$）和它的逆元组成的连串乘积，便发现这个子群已经是整个群，例如$r^2(=rr)=s,r^3(=rrr)=t$，$r^4(=rrrr)=e$.懂群论的读者自然晓得四元群只有上述两种结构，未学过群论的读者，如果你有耐性把四元群表填一填，也不难得出同样的结论.为了让自己对群这个概念更感亲切，这番工夫不妨一试的.

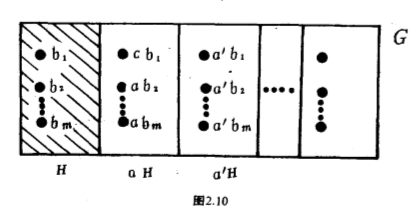
设$H$是$n$阶群$G$里的一个$m$阶子群，$H$的元是$b_1$、$b_2 $、$\cdots $、$b_m $.如果$m=n$，则$H$就是$G$，否则必有$G$中元$a$不在$H$里.考虑$ab_1 $、$\cdots $、$ab_m $，由消去律得知这是$m$个不同的元.它们都不在$H$时，否则如果某个$ab_i $是某个$b_j $，则$a=b_j b_i^{-1}$，由于$H$是个子群，而$b_j $和$b_i $都在$H$里，$b_j b_i^{-1}$也在$H$里，所以$a$应落在$H$里，这是个矛盾！我们把$\lbrace ab_1 ,\cdots ,ab_m \rbrace $这个集合记作$aH$，称为子群$H$的（左）陪集.如果$2m=n$，则$H$与$aH$合起来便是$G$，否则必有$G$的元$a’$既不在$H$里又不在$aH$里，也就是说$a’$不在$H$和$aH$的并集里.考虑$a’b_1 $、$\cdots $、$a’b_m$，这是$m$个不同的元，又都不在$H$与$aH$的并集里.这是因为像前面说的，它们不在$H$里；如果某个$a’b_i $是某个$ab_j $，则$a’=a(b_j b_i^{-1})$，由于$b_j b_i^{-1}$在$H$里，$a’$便落在$aH$里，这是个矛盾！依此类推，或者$3m=n$，则$G$是$H$与$aH$与$a’H$的并集，或者$3m\neq n$，便有$a’’$不在$H$或$aH$或$a’H$里，从而产生一个新的$a’’H$来.最后得到结论，$G$是由$H$和它的不同的陪集合并而成.设有$k$个不同的陪集，则$n=km$，$k$称为子群$H$的指数（图$2.10$）.因此，任何有限群$G$的子群$H$的阶必是$G$的阶的因子，这个貌简易明的结果是有限群论最基本的定理，首先见于法国数学家拉格朗日（$\mathrm{J.L.Lagrange}$）在$1770$年发表的论文上，通常称作拉格朗日定理.