这一节要介绍的群叫做置换群，其实在第$2.2$节里它们已登了场，但既然它们将要成为主角，我们不妨从头说起.所谓置换，就是把$N$个不同的东西的排列次序调换，说得精确一些，就是一个由这$N$个不同的东西组成的集自身之间的一一对应.为方便叙述，让我们把这$N$个不同的东西记作$1$、$2$、$\cdots $、$N$.一个置换$\sigma $可以表为

$$\begin{pmatrix}
1 & 2 & \cdots & N \\
\sigma (1) & \sigma(2) & \cdots & \sigma (N)
\end{pmatrix},$$

意指$N$对应于$\sigma (N)$，例如有五个不同的东西，把$1$和$2$调换，其余不动，得来的置换表为$\begin{pmatrix} 1 & 2 & 3 & 4 & 5 \\ 2 & 1 & 3 & 4 & 5 \end{pmatrix}$.$\begin{pmatrix} 1 & 2 & 3 & 4 & 5 \\ 3 & 2 & 4 & 1 & 5 \end{pmatrix}$这个置换，把$1$换作$3$，$2$不动，$3$换作$4$，$4$换作$1$，$5$不动.如果$\sigma_1 $和$\sigma_2 $是两个置换，它们的合成$\sigma_1 \sigma_2 $也是一个置换，效果是先按$\sigma_2$调换次序，再按$\sigma_1$调换次序.就拿刚才的两个置换为例，

$$\begin{pmatrix} 1 & 2 & 3 & 4 & 5 \\ 2 & 1 & 3 & 4 & 5 \end{pmatrix} \begin{pmatrix} 1 & 2 & 3 & 4 & 5 \\ 3 & 2 & 4 & 1 & 5 \end{pmatrix} =\begin{pmatrix} 1 & 2 & 3 & 4 & 5 \\ 3 & 1 & 4 & 2 & 5 \end{pmatrix} .$$

请注意$\sigma_1 \sigma_2 $与$\sigma_2 \sigma_1 $不一定相同，例如

$$\begin{pmatrix} 1 & 2 & 3 & 4 & 5 \\ 3 & 2 & 4 & 1 & 5 \end{pmatrix} \begin{pmatrix} 1 & 2 & 3 & 4 & 5 \\ 2 & 1 & 3 & 4 & 5 \end{pmatrix} =\begin{pmatrix} 1 & 2 & 3 & 4 & 5 \\ 2 & 3 & 4 & 1 & 5 \end{pmatrix} .$$

$N$个不同的东西的全部置换组成一个群，叫做$N$次对换群，记作$S_N$.它的阶是$N!(=1\times 2\times 3$ $\times \cdots \times (N-1)\times N)$，单位元是$\begin{pmatrix} 1 & 2 & \cdots & N \\ 1 & 2 & \cdots & N \end{pmatrix}$，$\begin{pmatrix} 1 & 2 & \cdots & N \\ \sigma (1) & \sigma (2) & \cdots & \sigma (N) \end{pmatrix}$的逆元是$\begin{pmatrix} \sigma (1) & \sigma (2) & \cdots & \sigma (N) \\ 1 & 2 & \cdots & N \end{pmatrix}$，例如有五个不同的东西，$\begin{pmatrix} 1 & 2 & 3 & 4 & 5 \\ 3 & 2 & 4 & 1 & 5 \end{pmatrix}$的逆元是$\begin{pmatrix} 3 & 2 & 4 & 1 & 5 \\ 1 & 2 & 3 & 4 & 5 \end{pmatrix}$，写得好看一些，即是$\begin{pmatrix} 1 & 2 & 3 & 4 & 5 \\ 4 & 2 & 1 & 3 & 5 \end{pmatrix}$.

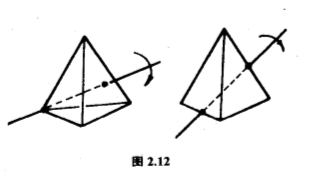
几何形体的对称群，通常可以表为一个$N$次对称群里的某个子群.例如正三角形的对称群，也就是$D_3$，里面每个元可以看做是三角形的三个端点的置换，由于全部六个置换都能实现，正三角形的对称群是整个$S_3$.正方形的对称群里每个元可以看做是正方形的四个端点的置换，但这次并非全部$24$个置换都能实现，所以正方形的对称群不是整个$S_4$，它只是$S_4$里一个$8$阶子群，结构与$D_4$相同.正四面体的对称群也是$S_4 $里的一个子群，每个元可以看做是正四面体的四个端点的置换.它也不是整个$S_4 $，因为镜像反影是没有实现的，例如$\begin{pmatrix} 1 & 2 & 3 & 4 \\ 1 & 4 & 3 & 2 \end{pmatrix}$不在对称群里.它也不是$D_4$，因为至少已有$9$个对称：绕着一条连接一个端点与它对面的中心的直线为轴旋转$120^{\circ}$和$240^{\circ}$，得到两对称；共有$4$条类似的对称轴，所以至少有$8$个对称，加上恒定不动，便至少有$9$个对称了.根据拉格朗日定理，这个群的阶是$\vert S_4 \vert =24$的因子，它不是$24$，又不小于$9$，便只能是$12$.因此，正四面体的对称群是个$12$阶群，除了刚描述的$9$个对称，再有$3$个，就是绕着一条连接一对棱的中心的直线为轴旋转$180^{\circ}$（图$2.12$）.用置换的写法，那$12$个元是

$$\begin{pmatrix} 1 & 2 & 3 & 4 \\ 1 & 2 & 3 & 4 \end{pmatrix} , \begin{pmatrix} 1 & 2 & 3 & 4 \\ 1 & 4 & 2 & 3 \end{pmatrix} ,\begin{pmatrix} 1 & 2 & 3 & 4 \\ 1 & 3 & 4 & 2 \end{pmatrix} ,$$

$$\begin{pmatrix} 1 & 2 & 3 & 4 \\ 4 & 2 & 1 & 3 \end{pmatrix} , \begin{pmatrix} 1 & 2 & 3 & 4 \\ 3 & 2 & 4 & 1 \end{pmatrix} ,\begin{pmatrix} 1 & 2 & 3 & 4 \\ 4 & 1 & 3 & 2 \end{pmatrix} ,$$

$$\begin{pmatrix} 1 & 2 & 3 & 4 \\ 2 & 4 & 3 & 1 \end{pmatrix} , \begin{pmatrix} 1 & 2 & 3 & 4 \\ 2 & 3 & 1 & 4 \end{pmatrix} ,\begin{pmatrix} 1 & 2 & 3 & 4 \\ 3 & 1 & 2 & 4 \end{pmatrix} ,$$

$$\begin{pmatrix} 1 & 2 & 3 & 4 \\ 3 & 4 & 1 & 2 \end{pmatrix} , \begin{pmatrix} 1 & 2 & 3 & 4 \\ 4 & 3 & 2 & 1 \end{pmatrix} ,\begin{pmatrix} 1 & 2 & 3 & 4 \\ 2 & 1 & 4 & 3 \end{pmatrix} .$$

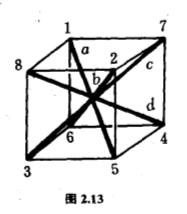
立方体的对称群是$S_8$的一个子群，看过这么多例子后，读者应该明白这个群不是整个$S_8$，只是$S_8 $里一个较小的子群.如果你留意到立方体有四条对角线（图$2.13$），而这四条对角线的任何置换总可以通过某个对称实现，你便知道立方体的对称群是$S_8$里的一个$24$阶子群，结构与$S_4$相同.例如$\begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\ 6 & 7 & 8 & 5 & 2 & 3 & 4 & 1 \end{pmatrix}$代表一个绕着横轴转$90^{\circ}$的对称，它把对角线$a=(1,5)$、$b=(2,6)$、$c=(3,7)$、$d=(4,8)$的次序调换，是$\begin{pmatrix} a & b & c & d \\ b & c & d & a \end{pmatrix}$.立方体的每一面的中心构成一个正八面体的$6$个端点，因此正八面体的对称群的结构与立方体的对称群相同.

正四面体的对称群，是$4$次对称群$S_4$里一个很特殊的子群，叫做$4$次交错群，让我们跟交错群也打个交道吧.首先，让我介绍一个把置换写作圈分解的表示方式，为了更好明白这个表示方式，把$1$、$2$、$\cdots $、$N$写在一个圆周上，如果$\sigma $把$i$换成$j$，即是$\sigma (i)=j$，便从$i$点至$j$点画一条有向的线段，例如$\begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 \\ 4 & 6 & 10 & 5 & 1 & 8 & 7 & 12 & 11 & 3 & 9 & 2 \end{pmatrix}$这个置换的图，如图$2.14$所示.

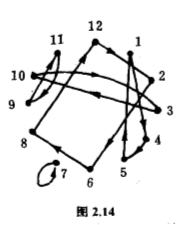
读者一定留意到这样的图总是由若干个圈组成，在上面的例子，共有$5$个圈，其中一个圈有四个点、一个圈有三个点、两个圈各有两点、一个圈只有一点.我们用$(a_1 ,a_2 ,\cdots ,a_m )$表示一个有$m$点的圈，意指从$a_1$走到$a_2$，$a_2 $走到$a_3$，$\cdots $，$a_{m-1}$走到$a_m $，$a_m $走到$a_1$.在上面的例子，那$5$个圈是$(2,6,8,12)$、$(1,4,5)$、$(3,10)$、$(9,11)$、$(7)$.其实一个圈$(a_1 ,a_2 ,\cdots ,a_m)$也是一个置换，它把$a_1$换作$a_2$、$a_2$换作$a_3$、$\cdots $、$a_{m-1}$换作$a_m $、$a_m $换作$a_1 $，其余不动.从这个角度看，这些圈的合成正好就是原来的置换，而且在结合过程中，由于每个圈含的点不落在另一个圈内，结合次序无关大局.在上面的例子，我们可以写成

$$\begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 \\ 4 & 6 & 10 & 5 & 1 & 8 & 7 & 12 & 11 & 3 & 9 & 2 \end{pmatrix}$$

$$=(1,4,5)(2,6,8,12)(3,10)(7)(9,11).$$

一般而言，任何置换$\sigma $能唯一（次序不计）表成若干个圈的乘积，叫做$\sigma $的圈分解.每个圈上的点数叫做它的圈长，圈长是$1$的圈即是单位元置换，圈长是$2$的圈叫做对换.我们把置换$\sigma $的圈分解里的圈的个数记作$l(\sigma )$，例如在上面的例子，$l(\sigma )=5$.

设$\sigma $是一个置换，而$\tau$是一个对换，你猜$\tau \sigma $与$\sigma $有什么好的关系呢？分两种情况讨论：

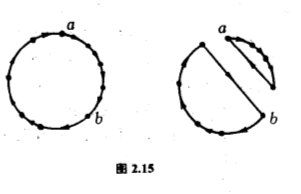
$(1)\;\tau =(a,b)$，$a$和$b$在$\sigma $的圈分解里同一个圈上，结合$\tau $后，效果等于把这个圈分裂为两个圈（图$2.15$）.

$(2)\;\tau =(a,b)$，$a$和$b$在$\sigma $的圈分解里不同的圈上，结合$\tau $后，效果等于把这两个圈合并为一个圈（图$2.16$）.

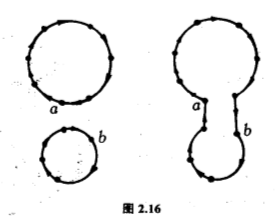
不论是哪一种情况，$l(\sigma )$与$l(\sigma \tau )$总是相差$1$.让我们定义$\sigma $的正负号函数作$\mathrm{sgn} (\sigma ) =(-1)^{N-l(\sigma )}$，则$\mathrm{sgn} (\tau \sigma )=-\mathrm{sgn} (\sigma )$.因此，如果$\sigma $是$k$个对换的乘积，则$\mathrm{sgn} (\sigma )=(-1)^k$，这是因为从定义可知$\mathrm{sgn} (e)=1$，$e$是单位元置换.每个置换是若干个圈的乘积，而每个圈又可以写作若干个对换的乘积，比方$(a_1 ,a_2 ,\cdots ,a_m )=(a_1 ,a_2 )(a_2 ,a_3 )\cdots (a_{m-2} ,a_{m-1} )(a_{m-1} ,a_m )$，所以任何置换可以写成若干个对换的乘积.这种写法可不是唯一的，因为把一个圈写成对换的乘积，有不同的方法，例如$(1,2,3,4,5)=(1,2)(2,3)(3,4)(4,5)$，但也有$(1,2,3,4,5)=(1,2)(2,4)(1,5)(4,5)(2,3)$ $(1,4)$.不过，$\mathrm{sgn} (\sigma )$却因$\sigma $而确定，与$\sigma $是多少个对换合成无关.根据刚才的正负号函数公式，我们知道虽然$\sigma $的对换乘积表示方式不唯一，对换的个数的奇偶性却是唯一的，因$\sigma $而确定.我们把$\mathrm{sgn} (\sigma )=1$的置换$\sigma $叫做偶置换，偶置换由偶数多个对换合成；把$\mathrm{sgn} (\sigma )=-1$的置换叫做奇置换，奇置换由奇数多个对换合成.如果$\sigma_1 $和$\sigma_2 $都是偶置换，它们的乘积$\sigma_1 \sigma_2 $也是偶置换，$e$当然是个偶置换，所以全部偶置换组成$S_N$里的一个子群，叫做$N$次交错群，记作$A_N$.如果$\tau $是个对换，它是个奇置换，所以对任何$A_N$中的元$\sigma $，$\tau \sigma $是奇置换，而且任何奇置换$\sigma’$也可以由这种做法得来，只用取偶置换$\tau \sigma’$，便有$\tau (\tau \sigma’ )=\tau^2 \sigma’ =\sigma’$.因此，$A_N$的阶正好是$S_N$的一半，即是$N!/2$，或者说，$A_N$的指数是$2$.

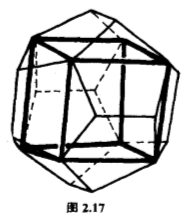
正四面体的对称群是$S_4$里的一个$12$阶子群，它其实与$A_4$的结构相同.众所周知，正多面体除了正四面体、立方体和正八面体外，还有两个，就是正十二面体和正二十面体.正十二面体每一面的中心构成一个正二十面体的十二个端点，所以它们的对称群是相同的.经过小心地计算（这儿不赘述），可以知道它们的对称群是$A_5$.从几何角度看，正十二面体里蕴藏了五个立方体（图$2.17$），每个正十二面体的对称，把这五个立方体的次序调换，所以正十二面体的对称群可以看做是$S_5$里的一个子群，正好是$A_5$.

以上谈了这么多的例子，都是某个$S_N$里的一个子群.凡是$S_N$里的子群，便叫做置换群，以上的例子，都是置换群.不难从它们的几何定义去理解，例如正三角形有三个端点，所以它的对称群是$S_3$的一个子群.但其实更抽象地，任何有限群都是置换群，说得更仔细些，任何$N$阶群都是$N$次对称群$S_N$里的一个子群.这是英国数学家凯莱（$\mathrm{A.Cayley}$）在$1878$年发现的著名定理.如果你审视群表，也许你会发现这一回事，群表的每一行都是首先的置换，而且行与行（看成是置换）的合成正好与首列相应的元的合成吻合.让我举一实例印证，一般的证明留待有兴趣的读者自己做吧.图$2.18$是矩形（非正方形）的对称群的群表，为易于比较我用了$1$、$2$、$3$、$4$分别代替$I$、$R$、$V$、$H$.对应于$3$的置换是$\begin{pmatrix} 1 & 2 & 3 & 4 \\ 3 & 4 & 1 & 2 \end{pmatrix}$，对应于$4$的置换是$\begin{pmatrix} 1 & 2 & 3 & 4 \\ 4 & 3 & 2 & 1 \end{pmatrix}$；$3$与$4$结合得$2$，对应于$2$的置换是$\begin{pmatrix} 1 & 2 & 3 & 4 \\ 2 & 1 & 4 & 3 \end{pmatrix}$,而正好$\begin{pmatrix} 1 & 2 & 3 & 4 \\ 3 & 4 & 1 & 2 \end{pmatrix} \begin{pmatrix} 1 & 2 & 3 & 4 \\ 4 & 3 & 2 & 1 \end{pmatrix} =\begin{pmatrix} 1 & 2 & 3 & 4 \\ 2 & 1 & 4 & 3 \end{pmatrix}$.所以这个四元群是$S_4$里的一个$4$阶子群.