让我们看一个既不是太复杂又不是太简单的例子，就是正方形的对称群.从第二章第$2.2$节和$2.7$节的讨论中我们知道这个群是八元二面体群$D_4$，亦可以看成是$4$次对称群$S_4$里的一个八阶子群，它的元是

$$x_0 =\begin{pmatrix}
1 & 2 & 3 & 4\\
1 & 2 & 3 & 4
\end{pmatrix} ,
x_1 =\begin{pmatrix}
1 & 2 & 3 & 4\\
4 & 1 & 2 & 3
\end{pmatrix} ,
x_2 =\begin{pmatrix}
1 & 2 & 3 & 4\\
3 & 4 & 1 & 2
\end{pmatrix} ,$$

$$x_3 =\begin{pmatrix}
1 & 2 & 3 & 4\\
2 & 3 & 4 & 1
\end{pmatrix} ,
x_4 =\begin{pmatrix}
1 & 2 & 3 & 4\\
4 & 3 & 2 & 1
\end{pmatrix} ,
x_5 =\begin{pmatrix}
1 & 2 & 3 & 4\\
1 & 4 & 3 & 2
\end{pmatrix} ,$$

$$x_6 =\begin{pmatrix}
1 & 2 & 3 & 4\\
2 & 1 & 4 & 3
\end{pmatrix} ,
x_7 =\begin{pmatrix}
1 & 2 & 3 & 4\\
3 & 2 & 1 & 4
\end{pmatrix} .$$

现在，让我们在正方形的四个角上放置标以$A$、$B$、$C$、$D$的四个球，每个角上放一个.如果正方形是固定不动的，便有$24$个不同的摆法，可以写作

$$(ABCD),(ABDC),(ACBD),\cdots .$$

像第一个摆法，是把$A$放在$1$号角、$B$放在$2$号角、$C$放在$3$号角、$D$放在$4$号角，其余类推.不过，这种表示方式可没有考虑到那四个角其实是不可区别的，例如$(ABCD)$和$(DABC)$貌易而实同，把前一个放置了球的正方形逆时针方向转$90^{\circ}$（即是$x_1$的作用）便得出后一个了.类似地，从$(ABCD)$经由正方形对称群的$8$个移动可得出$8$个互相貌易而实同的摆法，即是

$$(ABCD),(DABC),(CDAB),(BCDA),$$

$$(DCBA),(ADCB),(BADC),(CBAD).$$

但$(BACD)$却是一个貌异亦实异的摆法，不论你怎样移动正方形，都不能从$(ABCD)$得出$(BACD)$的.从$(BACD)$经由正方形对称群的$8$个移动可得出另外$8$个互相貌异而实同的摆法，即是

$$(BACD),(DBAC),(CDBA),(ACDB),$$

$$(DCAB),(BDCA),(ABDC),(CABD).$$

这$8$个摆法与前$8$个摆法合起来，共有$16$个，还欠$8$个才凑足$24$个摆法，这$8$个就是

$$(ACBD),(DACB),(BDAC),(CBDA),$$

$$(DBCA),(ADBC),(CADB),(BCAD).$$

从头一个经由正方形对称群的$8$个移动，可得出全部$8$个.所以，真正不同的摆法其实只有$3$个，就是

$$(ABCD),(BACD),(ACBD).$$

从这个例子我们清楚地见到关键所在，正方形对称群作用在全部构形上，把它们划分为若干类，每一类才是我们应该着眼的个体.要数数有多少个真正不同的构形，就是要数数有多少类.这种想法，导致群作用在集上的概念，为了方便以后叙述，容许我稍为抽象一些作个介绍.设$G$是一个群，$S$是一个集，对任意$G$中元$g$和$S$中元$s$规定二者结合产生某个$S$的元，记作$g\ast s$.这种结合关系满足以下两个条件：

$(1)\;$对$G$中元$g$、$h$和$S$中元$s$，有

$$g\ast (h\ast s)=(gh)\ast s.$$

$(2)\;$对$S$中元$s$，有$e\ast s=s$.

这里的$gh$表示$g$和$h$在$G$里的乘积，而$e$表示$G$的单位元.我们把这样的结合关系叫做$G$在$S$上的作用.熟悉高等数学名词的读者，都知道那等于说$G$在$S$上的作用是个从$G\times S$至$S$的映射，满足条件$(1)$和$(2)$.不过，读者即使不懂这些名词也不要紧，主要是明白其中涵义.见过前面的例子，读者对这个概念的其中涵义，应该觉得“司马昭之心，路人皆知”吧？比如说，$S$是全部$24$个摆法$(ABCD)$、$(ABDC)$、$(ACBD)\cdots \cdots $组成的集，$G$是正方形的对称群.$e$是$x_0$，即是不动，所以$e$作用于任何摆法$s$还是得出原来的摆法$s$，这即是条件$(2)$.考虑$s=(ABCD)$，$g=x_1 $，$h=x_5$.注意到$g$是逆时针方向转$90^{\circ}$的移动，$h$是绕着斜向右下角的对角线作轴翻转$180^{\circ}$的移动，$gh$是先$h$后$g$，相同于绕着横中线作轴翻转$180^{\circ}$的移动，即是$x_6$.先经$h$作用于$s$得出$s’=(ADCB)$，再经$g$作用于$s’$得出$(BADC)$，效果与直接经$gh=x_6$作用于$s$是相同的，这即是条件$(1)$.

按照刚才的例子，我们应该着眼于计算全部$g\ast s$，$s$是给定的，而$g$走遍群$G$.在刚才的例子里，这种计算的结果是把$S$的元划分为三类，一般而言，是否仍然有这个现象呢？让我们看看，为方便叙述，先引入以下的术语.给定$S$中的一个元$s$，全部$g\ast s$（$g$走遍$G$）组成一个$S$的子集，记作$G(s)$，叫做$s$的轨.用集合论的语言，这个写作$G(s)=\lbrace g\ast s\vert g\in G\rbrace $.不同的$s$可能产生不同的轨，但不同的轨必不相交，即是说两者没有公共的元.要说明这一回事并不难，让我只勾画证明的轮廓，留待读者自行补足细节.设$G(s_1)$和$G(s_2)$分别是$s_1$和$s_2$的轨，它们有一公共元$t$，要证明$G(s_1)$和$G(s_2)$是相同的集（图$3.1$）.

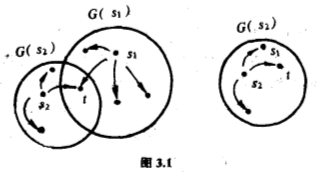
按定义，有$G$中元$g_1$和$g_2$使$t=g_1 \ast s_1 =g_2 \ast s_2$，所以

$$\begin{align}
s_1 & =e\ast s_1 =(g_1^{-1} g_1 )\ast s_1 \\
& =g_1^{-1} \ast (g_1 \ast s_1 ) \\
& =g_1^{-1} \ast (g_2 \ast s_2 ) \\
& =(g_1^{-1} g_2 )\ast s_2 ,
\end{align}$$

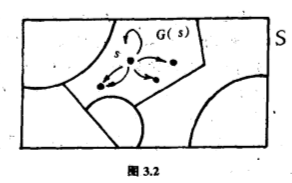
所以$s_1 $落在$G(s_2 )$里，从而全部$G(s_1 )$的元也落在$G(s_2 )$里；类似地可证明全部$G(s_2 )$的元也落在$G(s_1 )$里；所以$G(s_1 )=G(s_2 )$.每一个$S$的元必落在某个轨，具体地说，$s$落在$s$的轨$G(s)$，这是因为$s=e\ast s$.于是，我们知道$S$被划分为若干个轨，即是若干个互不相交的子集合并而成$S$（图$3.2$），我们要数的正是轨的个数.

在前面的例子里，有$3$个轨，每个轨有$8$个元.这样整齐的现象可不是常规，一般而言，轨的大小不是个个一样的.不如让我们多看一个例子，$G$仍然是正方形的对称群，$S$是全部在正方形的四个角上各放一个黑球或白球的摆法组成的集.这些摆法共有$2^4=16$个，可写作

（黑黑黑黑），（黑黑黑白），（黑黑白黑），$\cdots $.

其意自明，$G$在$S$上的作用，类似前述，它导致的轨共有$6$个，其中两个轨各个$1$个元、一个轨有$2$个元、三个轨有$4$个元（图$3.3$）.

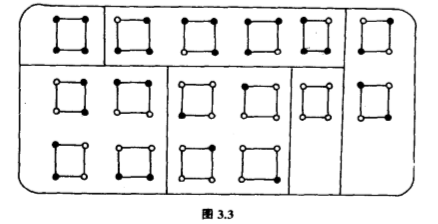
这$6$个轨代表了真正不同的摆法，其中一个用上四个黑球、一个用上三个黑球、两个用上两个黑球、一个用上一个黑球，一个没有用上黑球.

说到这儿，读者可能会问：“为什么把那些$G(s)$叫做轨呢？”试考虑无穷平面的旋转群$G$，$G$中每个元代表绕着平面上一个固定点逆时针方向旋转某个角度的移动，群的结合关系是旋转角的叠加.设$S$是平面的点组成的集，$G$在$S$上的作用就是经旋转后把原来一点移到它应去的位置上那一点.那么，$G(s)$是什么呢？请读者试自行画出来，看着图你便同意轨这个名字的确有贴切的几何意思.