《波利亚计数定理》三 “伯氏引理” 3.2 轨和稳定子群
现在,我们可以把问题表述成以下的形式:已知一个群$G$在一个集$S$上的作用,试计算轨的个数.如果每个轨的大小是一样,设有$k$个元,答案容易得出,就是$\vert S\vert /k$,$\vert S\vert $是$S$的元的个数.但上一节里第二个例子说明了一般情况并非如此,我们首先要计算的是每个轨有多少个元,这便引入稳定子群的概念了.让我们先理解为什么轨的大小不一样,那是因为可能存在$G$中元$g_1 $和$g_2 $,$g_1 \neq g_2 $,但$g_1 \ast s=g_2 \ast s$.如果没有那样的元,$g$走遍群$G$时,$g\ast s$个个不相同,于是每个轨都有$\vert G\vert $个元了.请注意,以上的说法等于说:存在$G$中元$g$,$g$不是单位元,但$g\ast s=s$.读者只要仿效上一节用过的做法,运用条件$(1)$和$(2)$便能证明这一回事,我不赘述了.我们把全部满足$g\ast s=s$的$g$收集在一起,它们不单组成$G$的一个子集,更组成$G$的一个子群,验证是直接计算,又是运用条件$(1)$和$(2)$,我也不赘述了.这个子群记作$G_s $,叫做$s$的稳定子群,用集合论的语言写作$G_s =\lbrace g\vert g\in G,g\ast s=s\rbrace $.请读者不要把$G_s $和$G(s)$混淆,前者是$G$的一个子群,后者是$S$的一个子集.
接着要说明的一个公式直觉上相当明显,但为了符合上一节的定义我们不得不作一点数学上的“装扮”,不如让我先道出公式的中心思想再去证明它吧.我们利用$G_s $把$G$划分成若干块,构成每一块的元正好是作用于$s$有相同效果的元,于是每一块便对应于轨$G(s)$一个元,有多少块$G(s)$便有多少元了.划分的办法是用$G_s$的元遍乘$G$的元,容易知道这样做每块有同样多的元,元的个数就是$G_s$的阶.因此,如果$G$的阶是$n$,$G_s $的阶是$m$,则$G$给划分成$n/m$块,所以轨$G(s)$也就有$n/m$个元了(图$3.4$).
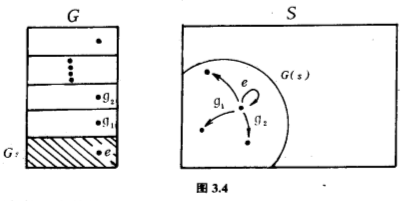
还记得第二章第$2.5$节的内容的读者,自然认得$n/m$这个数即是子群$G_s$的指数.现在让我们来证明这个公式:$G(s)$中元的个数等于稳定子群$G_s $的指数,先定义一个群$G_s $在$G$上的作用,对$G_s $中元$h$和$G$中元$g$,规定$h\ast g$是$gh^{-1}$($g$和$h^{-1}$在$G$里的乘积).不难验算那真的是个群在集上的作用,于是$G$给划分成轨$G_s (g)=\lbrace gh^{-1}\vert h\in G_s \rbrace $,$g$走遍群$G$.也不难验算每个轨$G_s (g)$有$m$个元,$G_s (g_1 )=G_s (g_2 )$当且仅当$g_1^{-1} g_2 $落在$G_s $里,亦即是说$g_1 \ast s=g_2 \ast s$.对每块$G_s (g)$规定$g\ast s$与它对应,这个对应与$g$在$G_s (g)$里的选取无关,而且不同的$G_s (g)$对应于不同的元$g\ast s$,任何$G(s)$的元又与某块$G_s (g)$对应,于是$G(s)$的元的个数等于块的个数,即是$n/m$,也即是子群$G$的指数.
有了上面的公式,我们终于能够说明一个非常有用的计数公式,也就是本书要讲述的中心理论的头一步.这个计数公式在很多书本中被称作“伯氏引理”(Burnside’s Lemma),因为它经由英国群论专家恩赛德(W.Burnside)的经典名著《有限群论》(第$2$版,$1911$年)而广泛流传.其实,早于$1845$年法国数学家柯西(A.L.Cauchy)已提出这个公式,后来德国数学家弗洛比尼斯(F.G.Frobenius)把它证明了.由于习称已久,本书姑且沿用“伯氏引理”这个名字,有兴趣想多知道一些有关史料的读者,可以参看以下的文章:
P.M.Neumann.A lemma that is not Burnside’s.The Mathematical Scientist,1979,4(2):133-141;

