让我们回到第$3.1$节的第二个例子，这是一个颇为典型的问题，值得我们多费一点笔墨把它纳入一个较广泛的结构，所以容许我采用一个较抽象的表述方式.

考虑两个集，$C=\lbrace 1,\cdots ,N\rbrace $和$R=\lbrace r_1 ,\cdots ,r_m \rbrace $.$S$是全部从$C$到$R$的映射组成的集，那即是说，$S$中的元$f$是这样的，它对每个$C$中元$x$对应一个$R$中元，记作$y=f(x)$.看看实例较易明白，在第$3.1$节那个例子里，$N=4,m=2$而$r_1 =$白，$r_2 =$黑.$S$中一个典型的元$f$是这样：$f(1)=$白、$f(2)=$白、$f(3)=$黑、$f(4)=$黑；它代表的自然是一个摆法：在$1$号角和$2$号角放白球，在$3$号角和$4$号角放黑球，也即是在第$3.1$节写的（白白黑黑）.$G$是$N$次对称群$S_N$里某个子群，我们定义群$G$在集$S$上的作用如下：对$G$中元$\pi $与$S$中元$f$，规定$\pi \ast f$是$f\pi $，即是$f$和$\pi $（两者都看做是映射）的合成.看看实例较易明白，在第$3.1$节那个例子里，$G$是正方形的对称群，看成是$S_4$的子群，元是$x_0 $、$x_1 $、$\cdots $、$x_7 $（见第$3.1$节），设$\pi =x_5 =\begin{pmatrix} 1234 \\ 1432 \end{pmatrix}$，$f$如上述.那么$f\pi (1)=f(1)=$白、$f\pi (2)=f(4)=$黑、$f\pi (3)=f(3)=$黑、$f\pi (4)=f(2)=$白，所以$f\pi $就是（白黑黑白），那即是经$x_5$的作用，把正方形翻转$180^{\circ}$后再逆时针方向转$90^{\circ}$，摆法从（白白黑黑）变成（白黑黑白）.要数数有多少个构形，就等于数数在这个作用底下有多少个轨.根据伯氏引理，我们只用计算每个$X(\pi )$有多少个元，然后代入公式.

给定$G$中一个元$\pi $，从第二章第$2.7$节的讨论中我们知道$\pi $有唯一的圈分解，圈分解里的圈的个数记作$l(\pi )$，比方刚才$\pi =x_5$，它的圈分解是$(1)(3)(2,4)$，$l(\pi )=3$.要求$f$满足$\pi \ast f=f$，就是要求$f\pi (1)=f(1)$、$f\pi (2)=f(2)$、$\cdots $、$f\pi (N)=f(N)$.要达到这个要求，只要$f$在每个圈上的点取相同的值便成，互相之间倒没有任何约束条件的.反之，这样的$f$一定满足$\pi \ast f=f$.例如刚才的$\pi =x_5$，$f(1)$可以取值白或黑，$f(3)$可以取值白或黑，$f(2)$和$f(4)$要同时取值白或同时取值黑；因此$X(\pi )=\lbrace f\vert \pi \ast f=f\rbrace $共有$2^3=8$个元，即是$\vert X(\pi )\vert =8$.一般而言，$\vert X(\pi )\vert =\vert R\vert ^{l(\pi )}$，所以轨的个数（也即是构形的个数）等于$\dfrac{1}{\vert G\vert } \sum \vert R\vert ^{l(\pi )}$，在这个求和式中，$\pi $走遍$G$.

让我们就着这个架构重复第$3.1$节第二个例子的计算吧，在这个例子中，$\vert G\vert =8$，$\vert R\vert =2$，$G$的$8$个元的圈分解是

$$x_0 =(1)(2)(3)(4),\quad x_1 =(1,4,3,2),$$

$$x_2 =(1,3)(2,4),\quad x_3 =(1,2,3,4),$$

$$x_4 =(1,4)(2,3),\quad x_5 =(1)(3)(2,4),$$

$$x_6 =(1,2)(3,4),\quad x_7 =(2)(4)(1,3);$$

所以$l(x_0 )=4$，$l(x_1 )=1$，$l(x_2 )=2$，$l(x_3 )=1$，$l(x_4 )=2$，$l(x_5 )=3$，$l(x_6 )=2$，$l(x_7 )=3$.在这个例子里，$\vert R=\vert =2$，因此构形的个数等于$(2^4+2^1+2^2+2^1+2^2+2^3+2^2$ $+2^3)/8=(16+2+4+2+4+8+4+8)/8=6$.利用这个更一般的公式我们可以同时轻易解决一大类的问题，最简单直接的一种推广是问：如果放在正方形四个角上的球不限于黑白两种颜色，可以是$m$种不同的颜色，那么共有多少个不同的构形呢？代入上面的公式，答案是

$$\begin{align}
& (m^4+m+m^2+m+m^2+m^3+m^2+m^3)/8 \\
= & (m^4+2m^3+3m^2+2m)/8.
\end{align}$$

如果颜色球有黑、白、红三种颜色，便有$21$个不同的构形；如果颜色球有黑、白、红、黄四种颜色，便有$55$个不同的构形，在这里不妨拿话岔开，从侧面欣赏伯氏引理的美妙.从上面的公式计算得来的答案既然是构形的个数，它一定是个正整数，也即是说，无论$m$是什么，$8$总整除$m^4+2m^3+3m^2+2m$.当然，用数学归纳法是不难证明这回事的，不过只凭肉眼不作计算，事前又不知道它代表某些构形的个数的话，是不易辨认出$m^4+2m^3+3m^2+2m$是$8$的倍数.

让我们转看另一个问题：用三种颜色的珠子可以串成多少条不同的长度是六颗珠子的项链呢？这个问题能轻易地纳入刚讨论过的架构，适用的群是$G=D_6$，看做是$6$次对称群$S_6$的子群，$C=\lbrace 1,2,3,4,5,6\rbrace $，$R=\lbrace r_1 ,r_2 ,r_3 \rbrace $，$S$的元$f$相应于串法，一条项链相应于在$G$的作用底下$S$里的一个轨，要数数有多少条项链，等于数数有多少个轨.如果读者动手计算一下，便知道$G$的$12$个元的圈分解的圈的个数分别是$6$、$1$、$2$、$3$、$2$、$1$、$4$、$3$、$4$、$3$、$4$、$3$.因此，轨的个数是$(3^6+3\times 3^4 +4\times 3^3 +2\times 3^2 +2\times 3)/12=92$，也就是说，共有$92$条不同花式的项链.

一个自然的推广是计算$m$种颜色的珠子可以串成多少条长度是$N$颗珠子的项链.适用的群是$G=D_N$，看做是$N$次对称群$S_N$的子群，$C=\lbrace 1,2,\cdots ,N\rbrace $，$R=\lbrace r_1 ,r_2 ,\cdots ,r_m $.$D_N$包含一个$N$阶循环子群，与$Z_N$有相同的结构，不如让我们先看看$Z_N$作用于$S$上的轨的个数吧.$Z_N$由单一个元生成，不妨设这个生成元是置换$\pi =\begin{pmatrix} 1 & 2 & 3 & \cdots & N-1 & N \\ N & 1 & 2 & \cdots & N-2 & N-1 \end{pmatrix} =(1,N,N-1,\cdots ,3,2)$，$l(\pi )=1$.要计算的是$l(\pi ^2)$、$l(\pi ^3)$、$\cdots $、$l(\pi ^N -1)$；至于$l(\pi ^N)=l(e)$，无须计算也知道那是等于$N$.举一个特例作说明吧，考虑$\pi ^3$，它把$1$换作$N-2$，把$N-2$换作$N-5,\cdots $，这样循环一周回到起点$1$，刚好跑遍$[N,3]/3$点，这里的$[N,3]$表示$N$和$3$的最小公倍数（图$3.5$）.

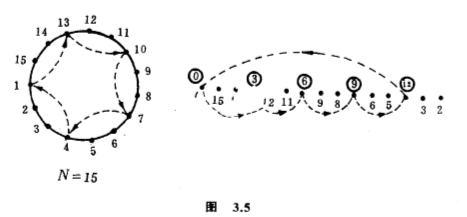
整个置换便是由这一类圈合成，每个圈的长度都是一样，所以圈的个数是$N\div [N,3]/3=3N/[N,3]=(N,3)$，这里的$(N,3)$表示$N$和$3$是最大公约数.类似地，$l(\pi ^k)=(N,k)$，根据上面的公式，轨的个数是$N(N,m)=\dfrac{1}{N} \displaystyle \sum_{k=1}^N m^{(N,k)}$.除了$Z_N$上的$N$个元以外，$D_N$还有另外一半的$N$个元，分别是把$\tau =\begin{pmatrix} 1 & 2 & 3 & 4 & \cdots & N-1 & N \\ 1 & N & N-1 & N-2 & \cdots & 3 & 2 \end{pmatrix}$.读者仔细分析一下，便知道这些元的圈分解有个特别的模式：如果$N=2n+1$（奇数），则每个元的圈分解有$n+1$个圈；如果$N=2n$（偶数），则一半的元的圈分解有$n$个圈，另一半的元的圈分解有$n+1$个圈（图$3.6$）.

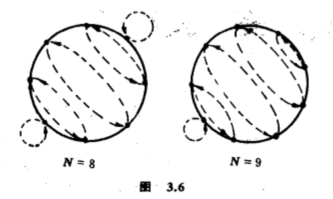
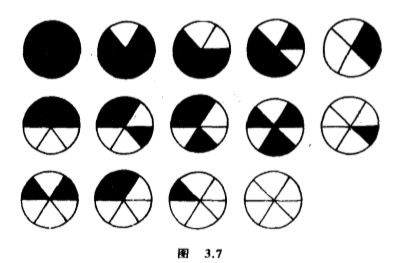
因此，轨的个数是$M(N,m)=\dfrac{1}{2N} \displaystyle \sum_{k=1}^N m^{(N,k)} +\dfrac{1}{2N} \sum_{k=1}^N m^{n+1}$或$\dfrac{1}{2N} \displaystyle \sum_{k=1}^N m^{(N,k)} +\dfrac{1}{2N} \sum_{k=1}^n m^n +\dfrac{1}{2N} \sum_{k=1}^n m^{n+1}$，视乎$N=2n+1$或$N=2n$.再化简一下，轨的个数是$M(N,m)=N(N,m)/2+A$，其中$A$是$m^{n+1}/2$或$(m+1)m^n/4$，视乎$N=2n+1$或$N=2n$.举一个实例，把圆盘分为相等的六个扇面，每一面涂上黑色或白色，共有多少个不同的圆盘呢（图$3.7$）？答案即是$N(6,2)$，从上式计算，那是$14$.假设圆盘是用透明塑料制成，翻转并无分别，共有多少个不同的圆盘呢？答案即是$M(6,2)$，从上式计算，那是$13$.请读者察看那$14$个圆盘（图$3.7$），试找出在第二种情况下哪一个是不需要的呢？

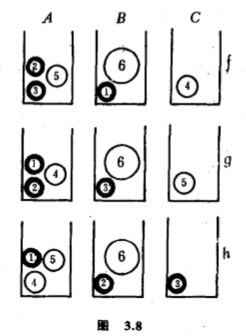
有些问题初看不像上述的模式，但换一个角度看，却可以纳入同一个架构.让我举以下的问题为例：有三只标以$A$、$B$、$C$的桶和六个球，其中三个是黑球，两个是白球，一个是红球，把这六个球分放在桶里，有些桶可以不放球，共有多少个不同的放置方法呢？读者不妨先想一想怎样把这个问题纳入上述的结构.显然，$C=\lbrace 1,2,3,4,5,6\rbrace$和$R=\lbrace A,B,C\rbrace $，$S$中元$f$是一个放置（有标号的）球的方法.设$1$号、$2$号和$3$号球是黑球、$4$号和$5$号球是白球、$6$号球是红球，那么在什么群的作用底下，$S$的轨才代表一个放置方法呢？看一个实例吧，设$f(1)=B$，$f(2)=A$，$f(3)=A$，$f(4)=C$，$f(5)=A$，$f(6)=B$；$g(1)=A$，$g(2)=A$，$g(3)=B$，$g(4)=A$，$g(5)=C$，$g(6)=B$；$h(1)=A$，$h(2)=B$，$h(3)=C$，$h(4)=A$，$h(5)=A$，$h(6)=B$.它们都是在桶$A$放置三个球，桶$B$放两个球，桶$C$放一个球的方法，不过$f$和$g$代表同一个放置方法，$h$却代表另一个放置方法.$f$和$g$代表的方法，桶$A$有两个黑球和一个白球，桶$B$有一个黑球和一个红球，桶$C$有一个白球；但$h$代表的方法，桶$A$有一个黑球和两个白球，桶$B$有一个黑球和一个红球，桶$C$有一个黑球（图$3.8$）.明白了这个道理，读者大概知道怎样写下适合的群吧，它是$6$次对称群$S_6$的子群，有$12$个元，写作圈分解表示，就是

$$\begin{array}{ll}
(1)(2)(3)(4)(5)(6), & (1)(4)(5)(6)(2,3), \\
(2)(4)(5)(6)(1,3), & (3)(4)(5)(6)(1,2), \\
(4)(5)(6)(1,2,3), & (4)(5)(6)(1,3,2), \\
(1)(2)(3)(6)(4,5), & (1)(6)(2,3)(4,5), \\
(2)(6)(1,3)(4,5), & (3)(6)(1,2)(4,5), \\
(6)(4,5)(1,2,3), & (6)(4,5)(1,3,2). \\
\end{array}$$

代入公式，轨的个数是$\dfrac{1}{12} (3^6+4\times 3^5+5\times 3^4 +2\times 3^3)=180$，所以共有$180$个不同的放置方法.

观察上面那个问题的两种极端情况，是有点教益的.第一种情况是把$N$个可区别的球（例如个个不同颜色）分放在$m$个标了号的桶里，考虑的$G$是单元群，只含单元$e$，$C=\lbrace 1,\cdots ,N\rbrace$和$R=\lbrace r_1 ,\cdots ,r_m \rbrace $.由于$\vert G\vert =1$和$l(e)=N$，不同的放置方法共有$m^N$个.读者大概会觉得好笑，割鸡焉用牛刀，只用注意每一个球有$m$个桶可放，第二个球也有$m$个桶可放，其余类推；合起来便有$m\times \cdots \times m$（$N$个）$=m^N$个不同的放置方法了.对的，对付这个问题的确无须动用伯氏引理，放在这儿只是为了印证一下上述的公式罢了.第二种情况是把$N$个不可区别的球（例如全部同一颜色）分放在$m$个标了号的桶，考虑的$G$是整个$N$次对称群$S_N$，$C=\lbrace 1,\cdots ,N\rbrace $和$R=\lbrace r_1 ,\cdots ,r_m \rbrace $.根据公式，轨的个数是$\sum m^{l(\pi )} /N!$，求和式中$\pi $走遍全部$N$次置换.例如$S_2 $中有$1$个置换分解成$2$个圈、$1$个置换分解成$1$个圈，所以共有$(m^2+m)/2=(m+1)m/2$个放置方法；$S_3$中有$1$个置换分解成$3$个圈、$3$个置换分解成$2$个圈、$2$个置换分解成$1$个圈，所以共有$(m^3+3m^2+2m)/6=(m+2)(m+1)m/6$个放置方法；$S_4$中有$1$个置换分解成$4$个圈、$6$个置换分解成$3$个圈、$11$个置换分解成$2$个圈、$6$个置换分解成$1$个圈，所以共有$(m^4+6m^3+11m^2+6m)/24=(m+3)(m+2)(m+1)m/24$个放置方法.目光锐利的读者（或者学过排列组合的读者）大概已看出规律，看来一般的答案似是$(m+N-1)(m+N-2)\cdots (m+1)m/N!$，也就是$(m+N-1)!/N!(m-1)!=\displaystyle {m+N-1 \choose N}$，后者符号$\displaystyle {x \choose y} $表示从$x$件不同的物件选出$y$件的全部方法个数.其实，有一个更容易计算出答案的方法，是把问题看成在$N$点之间插$m-1$条杠，把点分隔开来，例如$\cdot \cdot \vert \cdot \vert \vert \cdot $表示$1$号桶放$2$个球、$2$号桶放$1$个球、$3$号桶不放球、$4$号桶放$1$个球.更进一步，把问题看成在$N+(m-1)=m+N-1$件不同的物件（标了号的点连杆）选出$N$件（点），看看有多少个选法，那不正好是$\displaystyle {m+N-1 \choose N} $吗？从刚才的计算，我们知道这个数等于$\sum m^{l(\pi )} /N!$，求和式中$\pi $走遍全部$N$次置换.如果我们用$\bar{S} (N,k)$表示分解成$k$个圈的$N$次置换的个数，便得到

$$\dfrac{1}{N!} \sum_{k=1}^N \bar{S} (N,k)m^k ={m+N-1 \choose N} ,$$

在组合数学里这个$\bar{S} (N,k)$可有点名堂，它是$S(N,k)$的绝对值，后者称作第一类斯特林数（Stirling number of the first kind）,可以按照以下的递归计算式而得：

$$S(0,0)=1;$$

如果$N$和$k$都大于$0$，则

$$S(N,0)=S(0,k)=0;$$

如果$k$大于$N$，则

$$S(N,k)=0;$$

$$S(N,k)=S(N-1,k-1)-(N-1)S(N-1,k).$$

要从这样的定义推导上面的等式，涉及较多关于组合恒等式的知识，为了不把话题岔开，我不叙述了.

有时，我们需要小心选择群$G$，最显眼的群可不一定具最合用的样子，看看下面两个问题吧.第一个问题是：把正四面体的四个面涂上油漆，或涂红色，或涂绿色，共有多少个不同的花式呢？最显眼的群自然是正四面体的对称群，与$A_4$结构相同（见第二章第$2.7$节）.正四面体有四个面，每个面与它对着的端点正好来个一一对应.把每一面涂色，不妨看成把每个端点涂色，因此如同前面叙述过的例子完全一样，花式共有$\sum 2^{l(\pi )} /12 $，求和式中$\pi $走遍$A_4$.读者计算一下，便知道答案是$(2^4+11\times 2^2)/12=5$个.第二个问题是：把立方体的六个面涂上油漆，或涂红色，或涂绿色，共有多少个不同的花式呢？最明显的群自然是立方体的对称群，可以看做是$S_8$的子群，把八个端点置换，也可以看做是$S_4$的子群，把四条对角线置换.可惜立方体只有六面，我们不便利用$S_8$那个子群，也不便利用$S_4$那个子群，不能够像前一个问题直接套用那道公式，否则计算出的是另一回事！我们要看的是$S_6$的一个子群，它其实是原来的立方体的对称群，只是表成立方体六个面的置换.让我举一个实例作说明，$\begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\ 1 & 3 & 4 & 2 & 5 & 7 & 8 & 6 \end{pmatrix}$代表绕着连接点$1$和点$5$的对角线作轴旋转$120^{\circ}$这个对称（图$3.9$），它也可以表成$6$次对称群$S_6$的元$\begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6 \\ 3 & 5 & 6 & 2 & 4 & 1 \end{pmatrix} =(1,3,6)(2,5,4)$，右边的

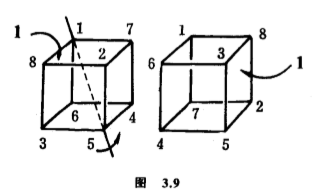
$1$表示由点$1$、点$2$、点$7$和点$8$组成的正方形，记作$\lbrace 1,2,7,8\rbrace $，类似地$2$表示$\lbrace 3,4,5,6\rbrace $、$3$表示$\lbrace 1,3,6,8\rbrace $、$4$表示$\lbrace 2,3,5,8\rbrace $、$5$表示$\lbrace 2,4,5,7\rbrace $、$6$表示$\lbrace 1,4,6,7\rbrace $.刚才的对称把面$1$换成面$3$、面$2$换成面$5$，其余类推.如果你把$24$个对称都用这种方式表成$S_6$的元，然后每个写下它的圈分解表示，再套用上述的公式，便计算出轨的个数，也就是不同的花式的个数了.（另一个较快捷的计算方法是利用那$24$个对称的几何解释，察看它们如何调换立方体的六个面，从而写下每个元的圈分解表示.）全部元的圈分解表示是：

$$\begin{array}{ll}
(1)(2)(3)(4)(5)(6), & (1)(2)(3,6,5,4), \\
(1)(2)(3,5)(4,6), & (1)(2)(3,4,5,6), \\
(4)(6)(1,3,2,5), & (4)(6)(1,2)(3,5), \\
(4)(6)(1,5,2,3), & (3)(5)(1,6,2,4), \\
(3)(5)(1,2)(4,6), & (3)(5)(1,4,2,6), \\
(1,3,6)(2,5,4), & (1,4,3)(2,6,5), \\
(1,4,5)(2,6,3), & (1,5,6)(2,3,4), \\
(1,6,3(2,4,5), & (1,3,4)(2,5,6), \\
(1,5,4)(2,3,6), & (1,6,5)(2,4,3), \\
(1,3)(2,5)(4,6), & (1,4)(2,6)(3,5), \\
(1,2)(3,6)(4,5), & (1,5)(2,3)(4,6), \\
(1,6)(2,4)(3,5), & (1,2)(3,4)(5,6), \\
\end{array}$$

所以不同的花式共有$(2^6+3\times 2^4+12\times 2^3+8\times 2^2)/24=10$个.当然，不惜伯氏引理单凭试验，这个答案也不难得来（见第一章第$1.2$节），但换了是$m$种油漆，单凭试验便无从得到$(m^6+3m^4+12m^3+8m^2)/24$这个答案了.在第一章第$1.2$节我们还提出一个貌似相同的问题：用逐面相隔的横直彩色线代替整面涂色，共有多少个不同的花式呢？即使是只有两种油漆（$m=2$）的情况，这个问题跟前一个问题的答案也不一样，因为这次合用的群不再是立方体的对称群，只是它的一个子群.举一个实例，$\begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\ 6 & 7 & 8 & 5 & 2 & 3 & 4 & 1 \end{pmatrix}$代表绕着横贯$\lbrace 1,3,6,8\rbrace $和$\lbrace 2,4,5,7\rbrace $这两个面的直线作轴旋转$90^{\circ}$这个对称，虽然它是立方体的对称，却不是画了横直彩色线的立方体的对称（图$3.10$）.

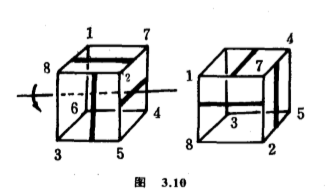
请读者选出那一个合用的子群，它的元是全部画了横直颜色线的立方体的对称，然后根据这些元的圈分解表示计算轨的数目，你将会发现答案是$12$个不同的花式（见第一章第$1.2$节）.一般而言，如果有$m$种油漆，答案是$(m^6+3m^4+8m^2)/12$.你把两个答案比较一下，便知道除了$m=1$的情况外，涂彩色线得来的花式总比涂整个面得来的花式为多，而且当$m$越大时，前者越接近后者的一倍.当$m=20$时，前者是$5\;373\;600$，后者是$2\;690\;800$；当$m=50$时，前者是$1\;303\;647\;500$，后者是$651\;886\;250$.

以上几个例子说明了怎样利用上述的一般架构去解决问题，不过我们也不要把这架构和公式视作万应灵丹，有很多场合它是硬套不上的.主要原因是$S$不一定囊括全部从$C$到$R$的映射，它可能只是某一部分从$C$到$R$的映射的集合.就取第一章第$1.1$节的问题为例：把一个黑球、一个红球、四个白球用棒连成一个正六边形，球在端点，共有多少个不同的构形呢？适合的群是$D_6$，$C=\lbrace 1,2,3,4,5,6\rbrace $，$R=\lbrace $白，黑，红$\rbrace $，但$S$并不是全部从$C$到$R$的映射组成的集合，它只包括那些映像是一个黑、一个红、四个白的映射.我们只好回到伯氏引理，直接计算那些$\vert X(\pi )\vert $了.考虑$D_6$的$12$个元，写成圈分解表示，是：

$$\begin{array}{ll}
(1)(2)(3)(4)(5)(6), & (1,6,5,4,3,2), \\
(1,5,3)(2,6,4), & (1,4)(2,5)(3,6), \\
(1,3,5)(2,4,6), & (1,2,3,4,5,6), \\
(1)(4)(2,6)(3,5), & (1,2)(3,6)(4,5), \\
(2)(5)(1,3)(4,6), & (1,4)(2,3)(5,6), \\
(3)(6)(1,5)(2,4), & (1,6)(2,5)(3,4). \\
\end{array}$$

对头一个元，在任何四个端点放白球，余下两个端点任意一个放黑球和一个放红球，得来的摆法经这个元的作用是不变，反之亦然，因此对这个元来说，$\vert X(\pi )\vert =2\times \displaystyle {6 \choose 4} =2\times 15=30$.对第$7$个元，在点$2$、$6$、$3$和$5$放白球，余下两个端点任意一个放黑球和一个放红球，得来的摆法经这个元的作用是不变，反之亦然，因此对这个元来说，$\vert X(\pi )\vert =2$.对第$9$个元和第$11$个元，计算也是一样.至于其他的元，经它的作用任何摆法总会给变更，所以$\vert X(\pi )\vert =0$.根据伯氏引理的公式，轨的个数是$(30+2+2+2)/12=3$，也就是说，不同的构形共有$3$个.读者可以自行计算正八面体和三棱柱体的情况（见第一章第$1.1$节），答案分别是$(30+9\times 2)/24=2$和$30/6=5$.你或许会问：“如果换了是两个黑球、两个白球、两个红球，岂不是又得从头推敲吗？而且不同的情况影响了$\vert X(\pi )\vert $的计算，每次得费神.有没有一个通用的方法呢？”有的，这就是本书的主题——波利亚计数定理，在第四章我们会展开讨论.

再多看一个例子，把立方体的六个面各涂上一种不同的颜色，又正好有六种颜色，红、橙、黄、绿、青、蓝，共有多少个不同的花式呢？适合的群是立方体的对称群，有$24$个元.由于每个面涂上不同的颜色，除单位元外，任何元作用于立方体都变更涂了色的样子；对单位元来说，却不变更全部$6!=720$个涂了色的样子当中任何一个.因此，不同的花式共有$720/24=30$个.如果换了规定，四个面不同颜色，是红、橙、黄、绿，两个面都是蓝色，计算便不相同了.除单位元外，任何元作用于立方体还是要变更涂了色的样子；对单位元来说，全部涂了色的样子都没一个给变更，但这次全部涂了色的样子只有$\displaystyle {6\choose 2} \times 4!=360$个，所以不同的花式共有$360/24=15$个.有兴趣的读者不妨自己拟定关于涂色的限制条件，逐个情况计算.虽然这番工夫颇耗时，但它却会使你更欣赏下面要介绍的波利亚计数理论.

作为这一节的结束，让我们提出一个有趣的问题，读者可以作为练习去解答.在硬卡纸片上写下一个三位数字，为了一致，我们同意把$0$写成$000$，把$1$写成$001$，把$2$写成$002\cdots \cdots $把$43$写成$043\cdots \cdots $现在问：顶多写多少张硬卡纸片（只写一面）便能用它们去展示从$0$至$999$这一千个数目呢？答案并不是$1000$，而是$945$.如果你习惯使用袖珍电子计算器，看惯那些以液晶体显示的数字的话，你甚至会得出一个更小的答案，是$846$.你愿试试吗？