在第二章第$2.2$节里我们介绍了平面或者空间里的对称，这节要讨论的是有限多个对称组成的群是一个什么模样.我们不考虑平移，所以全部对称都有一公共不动点，叫它作原点.要认真讨论这些对称，读者其实需要具备初等线性代数知识，更具体地，是正交矩阵与正交群的知识，但为了不把叙述岔开得太远，容许我提出以下两个事实作出发点，却不加以证明了：

$(1)$能在平面上实施的对称，必是绕着原点的旋转.

$(2)$能在空间里实施的对称，必是以通过原点的某条直线作轴的旋转.

先看平面的有限旋转群$G$，不妨假定$\vert G\vert \neq 1$.它的每个元$\pi $是绕着原点逆时针方向旋转$\theta $，记作$A(\theta )$.如果$A(\theta_1 )$和$A(\theta_2 )$是$G$的元，它们的乘积是$A(\theta_1 +\theta_2 )$.取最小的那个$\theta $，记作$\theta_0 $，那么任何$A(\theta )$都必定是$A(\theta_0 )$自乘若干次.这是因为$\theta =t\theta_0 +\varphi $，其中$t$是整数，$\varphi $是$0$或者在$0$和$\theta_0 $之间，所以$A(\theta )=A(\theta_0 )^t A(\varphi )$，即是$A(\varphi )=A(\theta_0 )^{-t} A(\theta )$.右边是一个$G$中的元，所以$A(\varphi )$也是$G$中的元，从$\theta_0$的选择得悉$\theta $只能是$0$，从而$A(\theta )=A(\theta_0 )^t$.结论是：$G$是个有限循环群，结构与$Z_N$相同，$N\theta =360^{\circ}$，它可以看作是一个正$N$边形的旋转对称群（不准翻转）.

现在看空间的有限旋转对称群$G$，也不妨假定$\vert G\vert \neq 1$.它的每个元$\pi $是绕着某条通过原点的直线作轴旋转，这条轴与以原点为中心的单位圆球面相交于两点，叫做$\pi $的极点.除去单位元不计，别的元都有两个极点，这两个极点也是对$\pi $来说在单位圆球面上唯一的两个不动点.设$\pi_1 $和$\pi_2 $是$G$中元，而$x$是$\pi_1 $的一个极点，那么$\pi_2 (x)$是$G$中元$\pi_2 \pi_1 \pi_2^{-1} $的极点，因为$\pi_2 \pi_1 \pi_2^{-1} (\pi_2 (x))=\pi_2 (x)$，而且$\pi_2 (x)$也是在单位圆球面上.考虑全部极点组成的集$S$，对$S$中元$x$和$G$中元$\pi $，规定$\pi \ast x=\pi (x)$，这定义了$G$在$S$上的一个作用.让我们计算在这个作用底下$S$有多少个轨.设有$r$个轨，根据伯氏引理，$r\vert G\vert =\sum \vert X(\pi )\vert $，求和式中$\pi $走遍$G$中元.如果$\pi $是单位元，$\vert X(\pi )\vert =\vert S\vert $；如果$\pi $不是单位元，$\vert X(\pi )\vert =2$.因此，$r\vert G\vert =2(\vert G\vert -1)+\vert S\vert =2(\vert G\vert -1)+\sum \vert G(x)\vert $，求和式中$x$走遍$r$个轨的代表元.记得$\vert G(x)\vert =\vert G\vert /\vert G_x \vert $，$\vert G_x \vert $是稳定子群，因此得到

$$r=2(1-1/\vert G\vert )+\sum 1/\vert G_x \vert ,$$

亦即

$$\sum (1-1/\vert G\vert )=2(1-1/\vert G\vert ) \label{1} \tag{*} $$

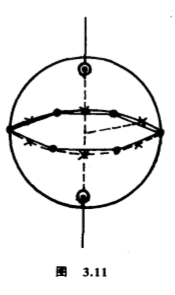
求和式中$x$走遍$r$个轨的代表元.注意到$1\leqslant 2(1-1/\vert G\vert ) < 2$和$1/2\leqslant 1-1/\vert G_x \vert < 1$，前者是因为$\vert G\vert \geqslant 2$，后者是因为$\vert G_x \vert \geqslant 2$（除单位元外还有另一个元以$x$为极点）.由此可以推断式$\eqref{1}$的左边求和式只能有$2$或$3$项，即是$r=2$或$3$，$S$只有$2$个轨或$3$个轨.让我们逐个情况考虑，设$r=2$，代入式$\eqref{1}$有$2=\vert G(x_1 ) \vert +\vert G(x_2 )\vert $，所以$\vert G(x_1 )\vert =\vert G(x_2 )\vert =1$.即是说，只有两个极点，各自成一轨，所以全部旋转都是绕着一条通过原点的公共轨.群的元把垂直于那条轴又通过原点的平面旋转，前面说过，这是个循环群.$G$可以看做是一个底是正多边形的棱锥的旋转对称群.其次，设$r=3$，代入式$\eqref{1}$有$1+2/\vert G\vert =1/\vert G_x \vert +1/\vert G_y \vert +1/\vert G_z \vert $.那三个$\vert G_x \vert $、$\vert G_y \vert $、$\vert G_z \vert $都不小于$2$，但又不能全部大于$2$，所以至少有一个是$2$，不妨置$\vert G_x \vert =2$.于是$1/2+2/\vert G\vert =1/\vert G_y \vert +1/\vert G_z \vert $.$\vert G_y \vert $和$\vert G_z \vert $中至少有一个不大于$3$，不妨置$\vert G_y \vert =2$或$3$，那么$\vert G_z \vert $不能大于$5$.总的来说，只有下列四种情况：$(a)\;\vert G_x \vert =\vert G_y \vert =2$，$\vert G_z \vert =n$（$n$大于$1$），$(b)\;\vert G_x \vert =2,\vert G_y \vert =3$，$\vert G_z \vert =3$，$(c)\;\vert G_x \vert =2,\vert G_y \vert =3$，$\vert G_z \vert =4$，$(d)\;\vert G_x \vert =2,\vert G_y \vert =3$，$\vert G_z \vert =5$.经仔细计算，每种情况都能精确地给描述出来，在这里我不详细写下计算了，有兴趣的读者可试自行补足细节.在情况$(a)$，$\vert G\vert =2n$，三个轨分别有$n$个点、$n$个点和$2$个点，其中一个轨的$n$个点正好是一个正$n$边形的端点，垂直于另一个轨的$2$个点连成的直线.$G$可以看做是一个正$n$边形在空间的旋转对称群，即是二面体群$D_n $（图$3.11$）.

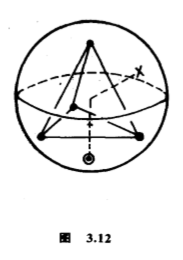
在情况$(b)$，$\vert G\vert =12$，三个轨分别有$4$个点、$4$个点和$6$个点，其中一个轨的$4$个点正好是一个正四面体的端点.$G$可以看做是一个正四面体的旋转对称群（图$3.12$）.

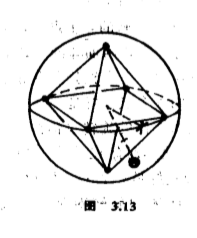
在情况$(c)$，$\vert G\vert =24$，三个轨分别有$6$个点、$8$个点和$12$个点，其中一个轨的$6$个点正好是一个正八面体的端点.$G$可以看做是一个正八面体的旋转对称群（图$3.13$）.

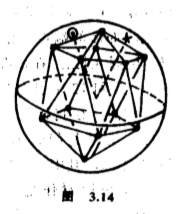
在情况$(d)$，$\vert G\vert =60$，三个轨分别有$12$个点、$20$个点和$30$个点，其中一个轨的$12$个点正好是一个正二十面体的端点.$G$可以看做是一个正二十面体的旋转对称群（图$3.14$）.

在这个例子里，读者看到一件奇妙的事.有限个旋转组成一个群，看似限制不多，结果凭着伯氏引理数一数，竟然发现它只能是几个熟悉的几何形体的旋转对称群！从这一点我们再一次体验到群和几何对称之间的关系.