在第三章第$3.4$节将近结束前提到一个亟须解决的问题，即是满足某些规定条件的构形计数问题.一个典型的例子是：把$e_1$个黑球、$e_2$个红球和$e_3$个白球（$e_1 +e_2 +e_3 =6$）用棒连成一个正六边形，球在端点，共有多少个不同的构形呢？固然，只要定了$e_1 $、$e_2 $、$e_3 $的值，利用伯氏引理我们懂得计算答案；走遍$e_1 $、$e_2 $、$e_3 $的取值范围，便得出全部答案了.但这样做挺费时，而且在计算全部$28$个情况的过程中，你会有种感觉，有部分计算是不必每次从头做起的.是否有更好的计算方法呢？

让我们重温一下伯氏引理的证明（见第三章第$3.3$节），为了做好推广的准备工作，我把证明的形式略作修改，多用了一点符号.也为了易于对比，我把$G$中元$g$和$S$中元$s$分别换记作$\pi $和$f$.设$\mathscr{S}$是全部满足$\pi \ast f=f$的有序偶$(\pi ,f)$组成的集，我们将用两种不同的看法计算$\vert \mathscr{S} \vert =\sum 1$，求和式中走遍$\mathscr{S}$中元$(\pi ,f)$.首先，$\vert \mathscr{S} \vert =\sum \left( \sum 1\right) $，外面的求和式中$\pi $走遍$G$中元，里面的求和式是选定了$G$中元$\pi $后走遍$\mathscr{S} $中元$(\pi ,f)$；因此，$\vert \mathscr{S} \vert =\sum \vert X(\pi )\vert $，求和式中$\pi $走遍$G$中元.其次，$\vert \mathscr{S} \vert =\sum \left( \sum 1\right) $，外面的求和式中$f$走遍$S$中元，里面的求和式是选定了$S$中元$f $后走遍$\mathscr{S} $中元$(\pi ,f)$；因此，$\vert \mathscr{S} \vert =\sum \vert G_f \vert $，求和式中$f$走遍$S$中元.由于$\vert G_f \vert =\vert G\vert /\vert G(f)\vert $，后一个式可改写成$\vert G\vert \sum 1/\vert G(f)\vert $，求和式中$f$走遍$S$中元.最关键的一步观察，就是留意到每个轨里的$f$提供的项合起来刚好是$1$，所以$\sum 1/\vert G(f)\vert $正好是轨的个数.因此，轨的个数是$\sum \vert X(\pi )\vert /\vert G\vert $，求和式中$\pi $走遍$G$中元.

按照上述思路，我们首先得决定怎样表述要计算的答案.上述计算只数了轨的个数，可没理会更细致的划分.比方开首那个例子，我们在第三章第$3.4$节里已经计算过，共有$92$个轨，每个轨即是一个构形.但在那个计算中，我们没办法知悉有多少个构形包含六个黑球，或者有多少个构形包含三个黑球、两个红球和一个白球.要作这样细致的记录，我们引入权的概念.可以这么说，权是一种记录的方法，但在数学上，好的记法往往带来意想不到的方便，以下的计算将会显示这一点.比方（红白黑白白白）这个摆法（图$4.1(a)$），我们把它写作（黑）$^1$（红）$^1$（白）$^4$，叫做它的权.

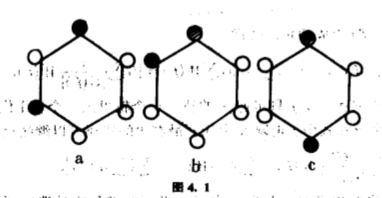
显然，经过对称群的作用，同一个轨里面的摆法有相同的权.但应注意，不同的轨里面的摆法，也可能有相同的权，例如（红黑白白白白）的权也是（黑）$^1$（红）$^1$（白）$^4$，但后者却不能由前者经对称群的作用得来（图$4.1(b)$）.规定颜色球数目后的构形计数问题，相当于给定某个权，数数有多少个轨有这样的权，举一个例子，考虑（黑）$^1$（红）$^1$（白）$^4$，共有$3$个轨，刚才已举了两个，剩下的一个包含（红白白黑白白）这个摆法（图$4.1(c)$）.相信读者已经晓得计算目标是什么吧？容许我把它写得抽象一点，以便建立一个较广泛的架构.沿用第三章第$3.4$节开首引入的表述方式，$S$的元是从$C=\lbrace 1,\cdots ,N\rbrace $到$R=\lbrace r_1 ,\cdots ,r_m \rbrace $的映射，记作$f$.如果$f$把$e_1 $个$C$的元对应于$r_1 $，$e_2 $个$C$的元对应$r_2 ,\cdots ,e_m$个$C$的元对应于$r_m (e_1 +\cdots +e_m =N)$，那么$W(f)=r_1^{e_1 } \cdots r_m^{e_m} $叫做$f$的权.同一个轨里面的元有相同的权，我们也把它叫做这个轨的权.从每个轨里选一个代表元$f$，把这些$f$的权加起来，再把相同的项合并，便得到$I(r_1 ,\cdots ,r_m )=\sum W(f) =\sum p_i W_i $，叫做构形计数记录.（有些书本的叙述采用级数形式表达，也把构形计数记录叫做构形计数级数，请看第五章第$5.3$节.）这里$W_i $表示全部出现的权，有$p_i $个轨的权是$W_i $.

仿效伯氏引理的证明，设$\mathscr{S} $是全部满足$\pi \ast f=f$的有序偶$(\pi ,f)$组成的集，考虑

$$\begin{align}
\vert G\vert I(r_1 ,\cdots ,r_m ) & =\vert G\vert \sum W(f) \\
& =\vert G\vert \sum \dfrac{1}{\vert G(f)\vert } W(f) ,
\end{align}$$

前一个求和式中$f$只走遍$S$的轨，每个轨里选一个$f$作代表；后一个求和式中$f$走遍$S$中元.最右边的式还可以继续化简成

$$\begin{align}
\sum \dfrac{\vert G\vert }{\vert G(f)\vert } W(f) & =\sum \vert G_f \vert W(f) \\
& =\sum (\sum W(f)),
\end{align}$$

外面的求和式中$f$走遍$S$中元，里面的求和式是选定了$S$中元$f$后走遍$\mathscr{S} $中元$(\pi ,f)$.把求和步骤调换了，便得到

$$\vert G\vert I(r_1 ,\cdots ,r_m )=\sum \left( \sum W(f) \right) ,$$

外面的求和式中$\pi $走遍$G$中元，里面的求和式是选定了$G$中元$\pi $后走遍$\mathscr{S}$中元$(\pi ,f)$.剩下来的工夫就是计算里面那个求和式.

设$\pi $的圈分解包含$l_1 (\pi )$个圈长是$1$的圈（即是不动点）、$l_2 (\pi )$个圈长是$2$的圈（即是对换）、$l_3 (\pi )$个圈长是$3$的圈$\cdots \cdots l_N (\pi )$个圈长是$N$的圈.注意，$l_1 (\pi )+\cdots +l_N (\pi )=l(\pi )$，就是$\pi $的圈分解里的圈的个数.设$f$满足$\pi \ast f=f$，那么$W(f)$是什么样子呢？在$l_1 (\pi )$个点上，$f$可以分别取任意值；$2l_2 (\pi )$个点上，$f$在每一对点上可以分别取任意值；$3l_3 (\pi )$个点上，$f$在每一组三个点上可以分别取任意值；$\cdots $；在$Nl_N (\pi )$个点上，$f$在全部$N$点上取任意但相同的值.比如$\pi =(2)(1,5)(3,4,6)$而$C=\lbrace a,b,c\rbrace $，那么$f$可以取值$f(2)=a$、$f(1)=f(5)=a$、$f(3)=f(4)=f(6)=b$，所以$W(f)=(a)(aa)(bbb)=a^3b^3$；$f$也可以取值$f(2)=c$、$f(1)=f(5)=b$、$f(3)=f(4)=f(6)=a$，所以$W(f)=(c)(bb)(aaa)=a^3b^2c$.也只有这种样子的$f$，才能满足$\pi \ast f=f$.一般而言，

$$W(f)=\underbrace {(r_{\ast } \cdots r_{\ast} )}_{l_1 (\pi )个} \underbrace {(r_{\ast }^2 \cdots r_{\ast}^2 )}_{l_2 (\pi )个} \cdots \underbrace {(r_{\ast }^N \cdots r_{\ast}^N )}_{l_N (\pi )个}$$

这里出现的$r_{\ast} $代表$\lbrace r_1 ,\cdots ,r_m \rbrace $中的元，容许重复.因此，在上一段的求和式中，

$$\sum W(f) =(r_1 +\cdots +r_m )^{l_1 (\pi )} (r_1^2 +\cdots +r_m^2 )^{l_2 (\pi )} \cdots (r_1^N +\cdots +r_m^N )^{l_N (\pi )} $$

从而

$$I(r_1 ,\cdots ,r_m )=\dfrac{1}{\vert G\vert } \sum (r_1 +\cdots +r_m )^{l_1 (\pi )} \cdots (r_1^N +\cdots +r_m^N )^{l_N (\pi )} ,$$

求和式中$\pi $走遍$G$中元.

让我们定义群$G$的圈指标（cycle index）作

$$Z_G (x_1 ,\cdots ,x_N )=\dfrac{1}{\vert G\vert } \sum x_1^{l_1 (\pi )} \cdots x_N^{l_N (\pi )} ,$$

求和式中$\pi $走遍$G$中元.于是，上述计算导致下面的重要公式，通常称作“波利亚计数定理”：

$$I(r_1 ,\cdots ,r_m )=Z_G (r_1 +\cdots +r_m ,r_1^2 +\cdots +r_m^2 ,\cdots ,r_1^N +\cdots r_m^N ).$$

如果你置$r_1 =\cdots =r_m =1$，那么全部$f$的权都化为$1$，构形计数记录也随着而化为轨的个数.代入上面的公式，轨的个数等于

$$\begin{align}
Z_G (m,m,\cdots ,m) & =\dfrac{1}{\vert G\vert } \sum m^{l_1 (\pi )} m^{l_2 (\pi )} \cdots m^{l_N (\pi )} \\
& =\dfrac{1}{\vert G\vert } \sum m^{l_1 (\pi )+l_2 (\pi ) +\cdots + l_N (\pi )} \\
& =\dfrac{1}{\vert G\vert } \sum m^{l(\pi )} \\
& =\dfrac{1}{\vert G\vert } \sum \vert R\vert ^{l(\pi )} ,
\end{align}$$

那不就是第三章第$3.4$节开首出现的伯氏引理的一个形式吗？

让我仍然以本章开首的问题为例去说明怎样运用波利亚计数定理.如果你已经计算了$D_6 $的$12$个元的圈分解（见第三章第$3.4$节），便知道$D_6 $的圈指标是

$$(x_1^6 +4x_2^3 +2x_3^2 +3x_1^2 x_2^2 +2x_6 )/12.$$

把黑球（以$a$代表）、红球（以$b$代表）或白球（以$c$代表）放在正六边形的端点上，得出多少种构形？每种有多少个？按照公式，这个问题的构形计数记录是：

$$\begin{align}
I(a,b,c)= & [(a+b+c)^6 +4(a^2+b^2+c^2)^3 + \\
& 2(a^3+b^3+c^3)^2 +3(a+b+c)^2 (a^2+b^2+c^2)^2+ \\
& 2(a^6+b^6+c^6)]/12.
\end{align}$$

如果你只对包含一个黑球、一个红球和四个白球的构形感兴趣，那你只用察看上面那个多项式展开后$abc^4$的系数是多少，答案是$3$.如果你把多项式完全展开，逐项写出来，便可以知道每种构形的个数.展开的多项式是

$$\begin{array}{l}
a^6+a^5b+a^5c+3a^4b^2+3a^4bc+3a^4c+3a^3b^3+ \\
6a^3b^2c+6a^3bc^2+3a^3c^3+3a^2b^4+6a^2b^3c+ \\
11a^2b^2c^2+6a^2bc^3+3a^2c^4+ab^5+3ab^4c+ \\
6ab^3c^2+6ab^2c^3+3abc^4+ac^5+b^6+b^5c+ \\
3b^4c^2+3b^3c^3+3b^2c^4+bc^5+c^6.
\end{array}$$

那就是说,有$1$个构形包含六个黑球、$1$个构形包含五个黑球和一个红球、$1$个构形包含一个黑球和一个白球、$3$个构形包含四个黑球和两个红球$\cdots $把上面那个多项式完全展开，凭手算可是不容易的事情，但那毕竟只是机械化操作，读者不应该被这种虽繁复枯燥却直截了当的计算引开了注意力而忽略了这道计算$I(r_1 ,\cdots ,r_m )$的公式的优美之处！应该注意的是群（对称）、权（记录）和多项式（计算）三者之间的有机结合，为一大类问题提供了有效巧妙的解决方法.

波利亚计数定理得名由来，是由于它出现在原籍匈牙利的美国数学家波利亚（$\mathrm{G.P\acute{o} lya}$）的一篇论文里.这篇长达$110$页的论文，题为“关于群、图与化学化合物的组合计数方法”（Kombinatorische Anzahlbestimmungen f$\mathrm{\ddot{u}}$r Gruppen,Graphen und Chemische Verbindungen.Acta Mathematica,$1937(68)\colon 145-254$），它有个特点，是全篇文章只环绕一条中心定理发挥，波利亚把这条定理叫做“主要定理”（Hauptsatz），就是上面的波利亚计数定理了.从这条定理衍生出来的各种应用，竟填满了$110$页的篇幅！而且，时至今日，过了半个多世纪后，这条公式还是广泛地用到各种计数问题上，波利亚计数理论也就成为组合数学里的一件极有力的工具，进入了通常的组合数学课程范围内.有兴趣的读者，可以参看瑞德（$\mathrm{R.C.Read}$）编著的《关于群、图与化学化合物的组合计数方法》（Combinatorial enumeration of groups,graphs,and chemical compounds.New York:Springer-Verlag,$1987$）附录一章.这本书的头一部分就是上面提到那篇波利亚经典之作的英译本，欲读第一手资料（而又不谙德文者）的读者不要错过.

不过，其实波利亚并不是头一位提出这套出色理论的数学家！第一位提出这套理论的人，是一位在当时籍籍无名的美国工程师列尔菲尔（$\mathrm{J.H.Redfield}$），他只发表了一篇论文，题为“群化分布的理论”（The theory of group-reduced distribution.American Journal of Mathematics.$1927(49)\colon 433-455$）.文章讨论对象是某种矩阵，列尔菲尔解决了这些矩阵的计数问题.为此他引入了“群化函数”，这正是$10$年后波利亚独立提出的“圈指标”.由于列尔菲尔采用的数学名词不普遍，当时没有什么人注意到这篇重要文章内涵的优美思想.即使$10$以后波利亚的文章发表了，仍然没有人把这两篇文章连上关系！在别的数学场合，列尔菲尔的文章也受到忽略，几乎完全没有被别人引用.自从$1940$年英国群论专家李特伍德（$\mathrm{D.E.Littlewood}$）在他的著作《群特征标理论》里面提过列尔菲尔这项工作后，又整整再过了$20$年美国图论专家哈拉利（$\mathrm{F.Harary}$）才把列尔菲尔这篇独特之作发掘出来！英国组合学专家罗伊德（$\mathrm{E.K.Lloyd}$）对这段历史很感兴趣，特地在$1976$年与列尔菲尔的家人联络上了（列尔菲尔本人早于$1944$年逝世），并从列尔菲尔的女儿手中获得一份她父亲的遗稿.这份文稿约于$1940$年写成，当时曾被投到《美国数学学报》，但没给发表退了回来.罗伊德把这篇文章寄给《图论学报》（Journal of graph theory），结果$1984$年第$8$期《图论学报》成为列尔菲尔纪念专辑，并且发表了这篇写成于将近半个世纪前的论文！有兴趣的读者可以参阅：E.K.Lloyd.Redfield’s papers and their relevance to counting isomers and isomerizations.Discrete Applied Mathematics,$1988(19)\colon 289-304$.有些书本把波利亚计数定理叫做波利亚-列尔菲尔定理，是有道理的；但在本书里，让我仍沿用旧称，只要大家不忘记列尔菲尔的功劳就是了.