让我们先看看怎样运用母函数尝试解决计数问题，所谓母函数就是一种形式幂级数，它的系数是满足某些条件的构形或者摆法的个数.形式幂级数是指它形如$u_0 +u_1 x+u_2 x^2 +\cdots $的式子，但我们不关心它的收敛性质，计算时也只是形式地套用四则运算法则，有点像$17$和$18$世纪的数学家把幂级数看成是多项式，只不过它有很多很多项而已！读者暂时不清楚这一点，不用担心，读下去便会明白的.

举一个最简单的例子吧，设$u_m $是从$N$件东西选出$m$件（不同）东西的方法的个数，那么$G(x)=u_0 +u_1 x+u_2 x^2 +\cdots $便叫这个计数问题的母函数.头一遭跟母函数打交道的读者心里可能嘀咕：“这只是一种记法吧，有什么了不起？”但是，正如我们在第四章第$4.1$节里已经说过，好的记法往往带来意想不到的方便！把众多情况的资料（那些$u_m$）集合于一个幂级数身上，在以后的计算中起了不可忽视的作用.上面的例子或许太简单，读者不容易看出这一点，但如果你懂得$u_m $其实是二项式系数$\displaystyle {N \choose m}$，便仍然会感觉得到母函数的优美之处，其实，$G(x)=(1+x)^N$.另一个看法是考虑$(1+x)\cdots (1+x)$，就是$1+x$自乘$N$次，$x^m $的系数等于从$N$项中选出$m$（不同）项的$x$的方法的个数，不正好是$u_m $吗？

让我再举一个稍为复杂的例子，设$u_m $是从$N$件东西选出$m$件（容许重复）东西的方法的个数.如同刚才把$1+x$自乘$N$次的想法，我们取$1+x+x^2+\cdots $自乘$N$次，每项代表一件东西，在该项选出$x^j$代表把那件东西选了$j$次.因此，$x^m $的系数正好是$u_m $.这里的无穷级数，$1+x+x^2+\cdots $是形式幂级数，形式地作运算，成立

$$(1+x+x^2+\cdots )(1-x)=1+x+x^2+\cdots -x-x^2-\cdots =1,$$

所以形式地$1/(1-x)=1+x+x^2+\cdots $.这个计数问题的母函数是$G(x)=1/(1-x)^N$.形式地我们可以作以下的计算，$G(x)=(1-x)^{-N} =1+b_1 x+b_2 x^2 +\cdots $，$b_m $是形式的二项式系数，等于

$$\begin{align}
(-N)(-N-1)(-N-2)\cdots (-N-m+1)(-1)^m/m! & =N(N+1)\cdots (N+m-1)/m! \\
& =\displaystyle {N+m-1 \choose m}.
\end{align}$$

因此，$u_m =b_m =\displaystyle {N+m-1 \choose m}$.如果读者套用第三章第$3.4$节介绍过的一个想法去直接计算这个$u_m $（注意，这儿的$N$和$m$应该分别看做是那儿的$m$和$N$），便更体会到母函数的优美了.

现在，我们可以解释凯莱的计算，但先要弄清楚什么叫做树图（以下简称作树）.一株树是一个这样的图：它的边并不构成圈；沿着它的边总可以从任一个点经过别的点走到任何一个点.看看下面的图（图$5.1$），你自然明白为什么这种图有这样的名字了.

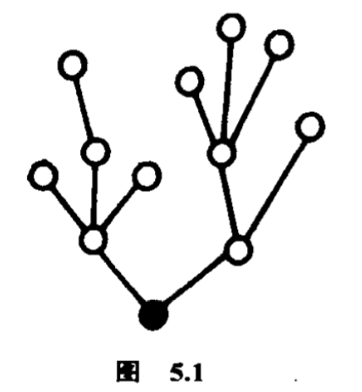
在树里选定一点，把它标为根（比如涂上颜色），这株树叫做有根树.现在的问题是：有$m$个点的有根树，共有多少株互不同构的？比方$m=4$时，共有四株（图$5.2$）.

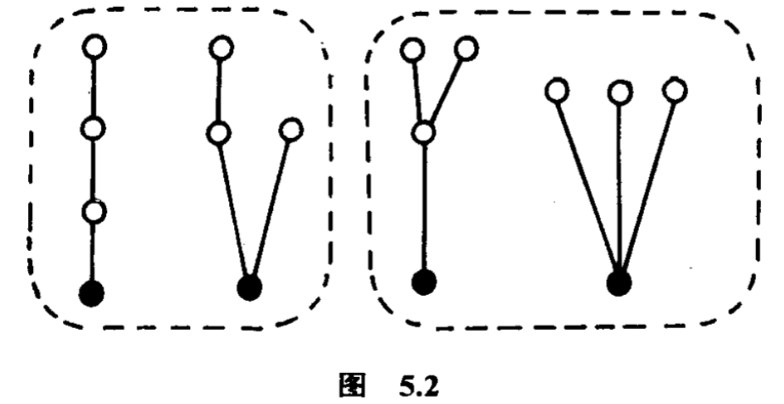
注意一点，如果没有标明一点作根，互不同构的$4$点树只有两株.把树中一点标作根提供了什么方便呢？一株有根树是由几株有根树接在根上生成，如果根的次数（即是连接那一点到别点的边的数目）是$k$，便有$k$株有根树接在根上（图$5.3$），这个简单的事实显示了根的次数的用途.

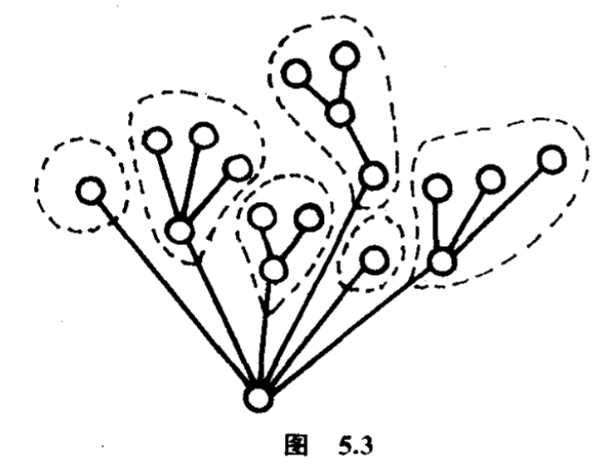
设$u_m $是$m$个点的有根树的个数，$u_m (k)$是$m$个点且根的次数是$k$的有根树的个数，那么$u_m =\sum u_m (k)$，求和式中$k$从$1$走到$m-1$.如果有$t_1 $株$1$点的树接在根上，$t_2 $株$2$点的树接在根上，$\cdots ,t_{m-1}$株$m-1$点的树接在根上，便成立$t_1 +\cdots +t_{m-1} =k$和$t_1 +2t_2 +\cdots +(m-1)t_{m-1} =m-1$，两个式合起来可以看成是一个把$m-1$分拆为$k$份的方法.比方上面的例（图$5.3$），树有$18$点，根的次数是$6$，有两株$1$点树、一株$3$点树、三株$4$点树接在根上，它提供的分析是$17=1+1+3+4+4+4$.要数数有多少株$m$个点且根的次数是$k$的有根树，只要数数有多少个不同的方法从$u_1 $株$1$点有根树选出$t_1 $株移植到根上、从$u_2 $株$2$点有根树选出$t_2 $株移植到根上$\cdots \cdots $这些数目亦不难计算，从$u_j $株$j$点有根树选出$t_j $株移植到根上，不同的方法共有$\displaystyle {u_j +t_j -1 \choose t_j }$个.所以，合起来便得到

$$u_m (k)=\sum \displaystyle {u_1 +t_1 -1 \choose t_1 } {u_2 +t_2 -1 \choose t_2 } \cdots {u_{m-1} +t_{m-1} -1 \choose t_{m-1} } $$

求和式走遍$m-1$分拆为$k$份（$k_1 +2k_2 +\cdots +(m-1)t_{m-1} =m-1$）的方法.把$u_m (1)$、$u_m (2)$、$\cdots $、$u_m (m-1)$加起来，但得到要计算的$u_m $了.理论上，知道$u_1 $、$u_2 $、$\cdots $、$u_{m-1} $，我们便能从这个叫人望而生畏的公式计算$u_{m+1}$，但实际做下去，这个算法不只繁复，更要命的是每次我们必须知道怎样把$m-1$分拆，以求写下那些$t_1 $、$t_2 $、$\cdots $.随着$m$增大，$m-1$的分拆方法迅速增加，叫人应付不来.比方当$m=20$时，$m-1=19$已经有$490$个分拆方法；当$m=100$时，$m-1=99$更有$169\;229\;875$个分拆方法呢！循这条途径作计算，不会走得很远，让我们看看如何运用母函数回避这点困难.置$u(x)=u_1 x+u_2 x^2 +u_3 x^3 +\cdots =x(u_1 +u_2 x+u_3 x^2 +\cdots )$，经形式运算（不理会收敛问题），得到

$$\begin{align}
u(x) & =x\sum \sum {u_1 +t_1 -1 \choose t_1 } \cdots {u_{m-1} +t_{m-1} -1 \choose t_{m-1} } x^{t_1 +2t_2 +\cdots +(m-1)t_{m-1} } \\
& =x\sum \sum {u_1 +t_1 -1 \choose t_1 } x^{t_1 } {u_2 +t_2 -1 \choose t_2 } x^{2t_2 } \cdots {u_{m-1} +t_{m-1} -1 \choose t_{m-1} } x^{(m-1)t_{m-1} } \\
& =x\sum \left[ {u_1 +t -1 \choose t} x^{t} \right] \left[ {u_2 +t -1 \choose t} x^{2t} \right] \cdot \left[ {u_3 +t -1 \choose t} x^{3t} \right] \cdots \\
& =x/(1-x)^{u_1 } (1-x^2)^{u_2 } (1-x^3)^{u_3 } \cdots .
\end{align}$$

在第一行和第二行的头一个求和式中$m$走遍$1$、$2$、$3$、$\cdots $，后一个求和式中$(t_1 ,\cdots ,t_{m-1} )$走遍$m-1$的分拆，使$t_1 +2t_2 +\cdots +(m-1)t_{m-1} =m-1$；在第三行的每项求和式中$t$走遍$1$、$2$、$3$、$\cdots $.凯莱早在$1857$年的一篇文章里已经发现了上面那个公式，利用这个无穷乘积表示式，我们无须用正整数的分拆方法便能计算$u_m $.其实，计算手续还是够繁复的，我们需要知道$u_1 $、$u_2 $、$\cdots $、$u_{m-1} $的值才能计算$u_m $的值，但较诸刚才动用正整数分拆方法作计算已经改良了好一大步.如果再运用一点形式微积分运算（这儿不赘述），还可以把上式换写成对数形式

$$u(x)=x\mathrm{exp} (\sum u(x^i)/i),$$

求和式中$i$走遍$1$、$2$、$3$、$\cdots $.继续运用微积分运算，我们能得到一个有效计算$u_m $的递归公式，凭着它不难算出

$$u(x)=x+x^2+2x^3+4x^4+9x^5+20x^6+48x^7+115x^8+286x^9+719x^{10} +\cdots .$$

一个点的有根树只有一株，两个点的有根树也只有一株，三个点的有根树有两株，这些都是显而易见.四个点的有根树有四株，我们已看过了（图$5.2$），读者愿不愿意画下那九株五个点的有根树呢？