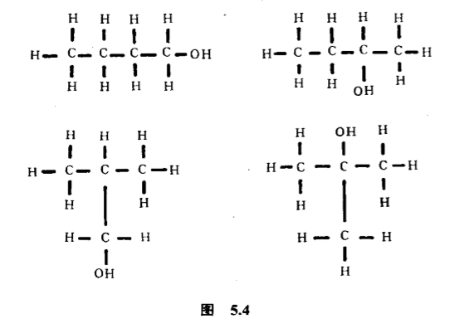
把烷烃$C_N H_{2N+2}$的一个氢原子换作基$X$，有多少个同分异构体？比方换作羟基（$OH$），丁醇$C_4 H_{10}O$有多少个同分异构体？答案是共有四个（图$5.4$）.

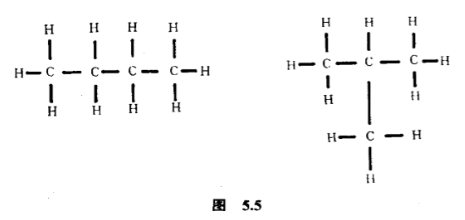
但丁烷$C_4 H_{10}$却只有两个同分异构体（图$5.5$），怎样从两个经取代得出四个呢？

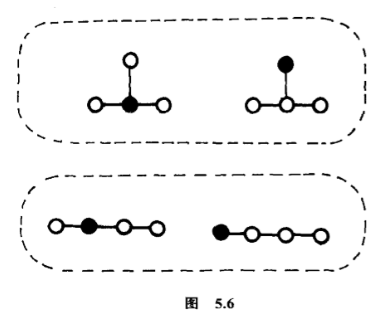
目光锐利的读者会从图中看到树的影子，重要的只是那些碳原子的位置，氢原子大可不必理会，于是那两个$C_4 H_{10}$的同分异构体变成是两株四个点的树，而那四个$C_4 H_{10} O$的同分异构体变成是四株四个点的有根树，根是连上羟基的碳原子（图$5.6$）.

在上一节我们已计算了$N$个点的有根树的数目，虽然对$N=1$、$2$、$3$或$4$，这个答案就是$C_N H_{2N+2} O$的同分异构体的个数，一般而言前者比后者多.化学上的条件限制，把问题变成：有多少株（互不同构）$N$个点的有根树，根的次数不大于$3$，每点的次数不大于$4$？

让我们回到波利亚计数定理，设$C=\lbrace 1,2,\cdots ,N\rbrace $和$R=\lbrace r_1 ,r_2 ,\cdots ,r_m \rbrace $，$S$是全部从$C$到$R$的映射$f$组成的集合.在第四章第$4.1$节里我们定义了$f$的权$W(f)$，$S$的轨的权分布表写为构形计数记录$I(r_1 ,r_2 ,\cdots ,r_m )$，定理说

$$I(r_1 ,\cdots ,r_m )=Z_G (r_1 +\cdots +r_m ,r_1^2 +\cdots +r_m^2 ,\cdots ,r_1^N +\cdots +r_m^N ),$$

$Z_G (x_1 ,\cdots ,x_N )$是作用在$S$上的群$G$的圈指标.在这一节要面对的计算，$R$是个无穷集，我们需要把上面的分式稍作装扮.其实波利亚在他的文章里本来就是以无穷形式表述计数定理的，但为了集中注意力于群的对称上，我们在第四章把讨论规限于有穷集$R$的情况.

每个$R$的元有个权，为方便叙述，不妨用$0$、$1$、$2$、$\cdots $作为$R$的元的权.虽然$R$有无限多个元，让我们仍然规定对每个$m$，只有有限多个$R$的元的权是$m$，设为$u_m $个.$R$的元的权分布可以写作一个母函数$u(x)=u_0 +u_1 x+u_2 x^2 +\cdots $.对$S$中元$f$我们定义$W(f)$作$f(1)$、$\cdots $、$f(N)$的权的和，叫做$f$的权.同一轨的元有相同的权，就叫做那个轨的权.设$G_m$是权为$m$的轨的个数，$S$的轨的权分布表写作母函数

$$G(x)=G_0 +G_1 x+G_2 x^2 +\cdots $$

波利亚计数定理说

$$G(x)=Z_G (u(x) ,u(x^2) ,\cdots ,u(x^N)),$$

$Z_G$是作用在$S$上的群$G$的圈指标.证明这个公式的方法跟第四章第$4.1$节的方法相似，设$\mathscr{S}_m $是全部满足$\pi \ast f=f$和$W(f)=m$的有序偶$(\pi ,f)$组成的集，考虑形式幂级数$\vert \mathscr{S}_0 \vert +\vert \mathscr{S}_1 \vert x+\vert \mathscr{S}_2 \vert x^2 +\cdots =\sum \left( \sum 1\right) x^m $，头一个求和式中$m$走遍$0$、$1$、$2$、$\cdots $，后一个求和式中走遍$\mathscr{S}_m $的有序偶.如同以前一样做法，先选定$f$后走遍$\pi $，再选定$\pi $后走遍$f$，两个答案合在一起就得到了公式了.举一个例子：把非负整数$k$分拆为三个非负整数（不计各加数的顺序），共有多少个不同的方法？比方$2$有两个，即是$0+0+2$和$0+1+1$；$6$却有七个，即是$0+0+6$、$0+1+5$、$0+2+4$、$0+3+3$、$1+2+3$、$1+1+4$、$2+2+2$.读者想一想，便知道这个问题可以纳入上述公式的架构，$G$是三次对称群$S_3 $，$u(x)=1+x+x^2+\cdots $，每个轨代表一个分拆方法.$S_3$的圈指标是$(x_1^3 +3x_1 x_2 +2x_3 )/6$，所以轨分布的母函数是

$$\begin{align}
G(x) =& [(1+x+x^2+\cdots )^3 +3(1+x+x^2+\cdots )\cdot \\
& (1+x^2+x^4+\cdots )+2(1+x^3+x^6+\cdots )]/6 \\
= & 1+x+2x^2 +3x^3+4x^4+5x^5+7x^6+8x^7+10x^8+\cdots ,
\end{align}$$

就是说，$0$和$1$都只有一个分拆方法、$2$有两个、$3$有三个、$4$有四个、$5$有五个、$6$有七个、$7$有八个、$8$有十个，等等.

现在可以开始数数有多少株$N$个点的有根树，其中根的次数不大于$3$，每点的次数又不大于$4$.这也等于数数有多少个烷醇$C_N H_{2N+2}O$的同分异构体.可以分为四种情况考虑，根的次数分别是$k=0$、$1$、$2$、$3$.如果根的次数是$k$，一株这样的树是把$k$株类似的树接在根上生成（图$5.7$）.

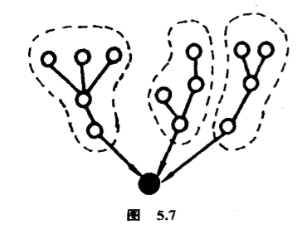
固然，把那$k$株树互相调换位置，是无关痛痒的.也就是说，在$k$次对称群$S_k $的作用下，一个轨代表一株不同的树.$S$是什么呢？$S$中元是从$\lbrace 1,2,\cdots ,k\rbrace $到$R$的映射，$R$就是全部满足上述条件的有根树组成的集，每株树的权是树上的点的个数.如果满足上述条件的$N$点有根树的个数是$A_N$，那么$u(x)=A_1 x+A_2 x^2 +A_3 x^3 +\cdots $便是$R$中元的权分布的母函数.设$G_k (x)=G_k (0)+G_k (1)x +G_k (2)x^2+\cdots $是轨分布的母函数，$G_k (m)$就是根的次数是$k$而每点次数又不大于$k$的$m+1$点有根树的个数.根据波利亚计数定理，有

$$G_k (x)=Z_G (u(x),u(x^2),\cdots ,u(x^k)),G=S_k ,$$

当$k=0$时，显然$G_0 (x)=1$.当$k=1$时，$Z_G (x_1 )=x_1 $，所以$G_1 (x)=u(x)$.当$k=2$时，$Z_G (x_1 ,x_2 )=(x_1^2 +x_2 )/2$，所以$G_2 (x)=[u(x)^2 +u(x^2)]/2$.当$k=3$时，$Z_G (x_1 ,x_2 ,x_ 3 )=(x_1^3 +3x_1 x_2 +2x_3 )/6$，所以$G_3 (x)=[u(x)^3 +3u(x)u(x^2)+2u(x^3)]/6$.巧妙的事情是$u(x)$本身却又跟$G_0 (x)$、$G_1 (x)$、$G_2 (x)$、$G_3 (x)$扯上另一种关系！这是因为

$$A_1 =G_0 (0)+G_1 (0)+G_2 (0)+G_3 (0),$$

$$A_2 =G_0 (1)+G_1 (1)+G_2 (1)+G_3 (1),$$

$$A_3 =G_0 (2)+G_1 (2)+G_2 (2)+G_3 (2),$$

$$\cdots ,$$

合起来即是$u(x)=xG_0 (x)+xG_1 (x)+xG_2 (x)+xG_3 (x)$，代入刚才的计算，得到

$$\begin{align}
u(x) = & x\lbrace 1+u(x)+[u(x)^2+u(x^2)]/2+ \\
& [u(x)^3 +3u(x)u(x^2) +2u(x^3)]/6\rbrace ,
\end{align}$$

置$A(x)=1+u(x)=1+A_1 x+A_2 x^2 +A_3 x^3 +\cdots $，上式化为$A(x)=1+[A(x)^3+3A(x)A(x^2)+2A(x^3)]/6$.如果我们已经知道$A_1 $、$A_2 $、$\cdots $、$A_N$的值，便可以从这个公式计算$A_{N+1}$的值，尤其利用电子计算机程序，这是容易办到的.下面是$N$从$1$到$20$的$A_N$的数值：

$$\begin{matrix}
N & A_N & N & A_N \\
1 & 1 & 11 & 1\;238 \\
2 & 1 & 12 & 3\;057 \\
3 & 2 & 13 & 7\;639 \\
4 & 4 & 14 & 19\;241 \\
5 & 8 & 15 & 48\;865 \\
6 & 17 & 16 & 124\;906 \\
7 & 39 & 17 & 321\;198 \\
8 & 89 & 18 & 830\;219 \\
9 & 211 & 19 & 2\;156\;010 \\
10 & 507 & 20 & 5\;622\;109 \\
\end{matrix}$$

$A_N$也就是烷醇$C_N H_{2N+2} O$的同分异构体个数，例如甲醇和乙醇各有一个、丙醇有两个、丁醇有四个、戊醇有八个，等等.$A_N$的数值增大得很快，利用他的计数定理波利亚还寻求了当$N$无限增大时$A_N$的渐近公式，得到$A_N \sim c^{-N} N^{-3/2} $，$c$是一个常数，约是$0.355$，其实是幂级数$A(x)$的收敛半径.从这渐近式不难推导出当$N$增大时，$A_{N-1} \sim (1/c)A_N$，或者说$A_N$渐近于一个几何级数.其实化学家早于这个世纪的$30$年代已经留意到这个现象，只是不懂如何解释吧.