从第一章的一些具体例子中已经知道，在映射$\omega =f(z)$之下，曲线被映为曲线.下面我们将给出两条曲线在它们交点处的夹角的定义，并研究在映射$\omega =f(z)$之下夹角的变化.当然我们的研究仅局限于一些最简单、最初等的例子，但是它们仍然说明了复变函数理论中的一些非常重要的思想.在这些例子中，映射$\omega =f(z)$都是保持曲线交角不变的，因而称为保角映射或保角变换.保角映射的理论是复变函数论的一个重要组成部分，它不但在理论研究中具有重要的作用，而且在应用上也是很有用的一部分.在力学、空气动力学、弹性力学、电学以及热学中都要用到保角映射.例如在许多问题中都要处理在电荷周围的电位势问题，或处理一个热体周围的温度分布问题，或者处理在稳定流体中流体在障碍物周围的流速问题.对于一般形状的带电体、带热体或障碍体，计算位势、温度或流速并不是一件容易的事情，为了克服这一困难，我们常借助保角变换，将它们化为最简单的形状，例如，为了设计飞机的翅膀，需要计算空气流过机翼时的速度.图$2.1(a)$是机翼的横断面，经过一个适当的保角变换（本章的后面将要给出）这个断面可化为圆（图$2.1(b)$，这时物体本身考虑为圆柱形），而对圆来说，计算特别简单，然后再化回去，就可以得原来要求的东西了.

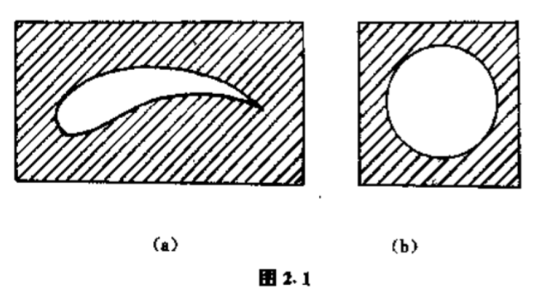
这样一来，保角映射为我们提供了一种计算位势、温度及流速等物理量的有力工具.这就说明了研究保角变换多么重要，本章将介绍一些初等的、但是重要的保角变换，并给出两个著名的应用.

线性变换

我们称

$$\omega =az+b\label{1.1} \tag{1.1}$$

为线性函数，其中$a$、$b$为复常数.设$k=\vert a\vert $，$\alpha =\arg{a} $.则$a=ke^{i\alpha }$.函数$\eqref{1.1}$便可分解为

$1)$ $z_1 =e^{i\alpha } z,$

$2)$ $z_2 =k z_1 ,$

$3)$ $\omega =z_2 +b.$

回忆一下复数四则运算的几何意义，我们就可看出，$(1)$是平面$z$旋转一个$\alpha $角度，$(2)$是平面$z_1 $的一个相似变换（伸长或压缩），而$(3)$是整个$z_2 $平面沿固定向量$b$所做的平移.

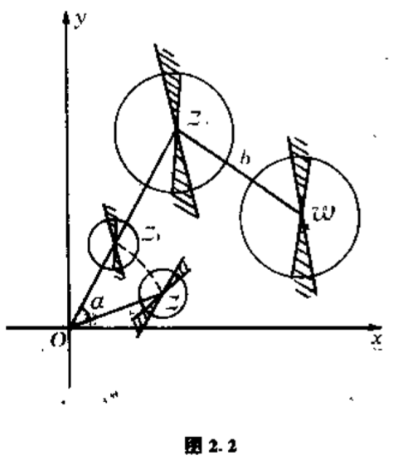
由线性函数所实现的映射称为线性变换或线性映射.由上面的讨论知，线性映射是上面三种最简单的映射的复合.由此便可以知道，映射$\eqref{1.1}$在全平面是一一的，并且把直线仍变为直线，而且保持两直线间的交角不变，把圆周仍变为圆周（图$2.2$）.

曲线间的夹角

前面我们指出，线性变换把直线变为直线，并保持直线间的交角不变，其实线性变换不仅保持直线间夹角，而且还保持曲线间的夹角.如何理解曲线间的夹角呢？

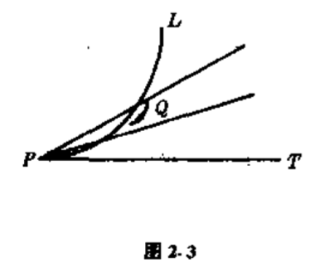
为此，我们先研究曲线在一点的切线的概念.从中学数学中读者可以知道，圆在一点的切线就是过那一点与半径垂直的直线.对于一条一般的曲线，切线概念的引入就要稍微复杂一些了，设$L$是一条曲线，$P$是$L$上的一点，我们来研究如何定义曲线$L$在点$P$的切线.在$L$上另取一点$Q$，用直线连接$P$、$Q$两点，得到曲线$L$的一条割线$\overline{PQ}$.让点$Q$沿着曲线$L$向点$P$移动，割线$\overline{PQ}$也就跟着点$Q$移动.现在让点$Q$无限接近于点$P$，如果割线$\overline{PQ}$的极限位置存在，那么，它的极限位置$PT$就称为曲线$L$在点$P$的切线（图$2.3$）.

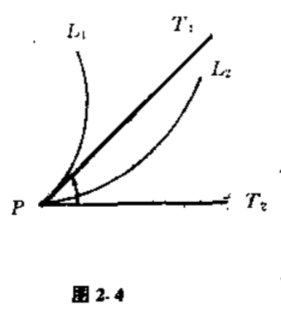
现在可以定义曲线间的夹角了.设曲线$L_1 $与$L_2 $交于点$P$，并假定曲线$L_1 $与$L_2 $在点$P$都有切线，它们的切线分别是$PT_1 $与$PT_2 $.我们就将$PT_1 $与$PT_2 $间的夹角定义为曲线$L_1 $与$L_2 $的夹角（图$2.4$）.

当两条相交曲线在交点具有同一条切线时，它们的夹角为零（图$2.5$）.

当$L_1$是一条曲线，而$L_2 $是一直线时，它们在交点$P$处的夹角定义为$L_1 $在点$P$处的切线$T_1 $与直线$L_2 $的夹角（图$2.6$）.

$\omega =z^n(n\geqslant 2)$所实现的变换

这一段我们研究函数

$$\omega =z^n \;(n\geqslant 2)\label{1.2} \tag{1.2} $$

实现的变换，并证明除去可能的例外点以外，它是处处保角的.我们从$\omega =z^2$开始，这个变换弄清楚了，一般情况就不难了.

$\omega =z^2 $有一个例外点，这个例外点就是$z=0$.在原点$O$处这个函数所实现的变换不保角.

从原点$O$出发引一条射线$OM$，假定它和$x$轴正向的夹角为$\varphi $（图$2.7$）.

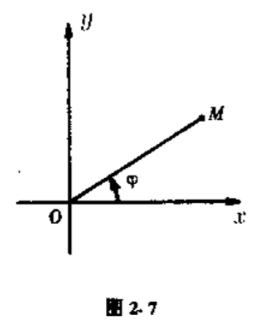
在射线$OM$上的每个点$z$，都有$\arg{z} =\varphi $.由复数的乘法，得

$$\vert \omega \vert =\vert z\vert ^2 ,$$

$$\arg{\omega } =2\arg{z} .$$

这样一来，向量$z$伸长$\vert z\vert $倍，再旋转一个角度$\arg{z} =\varphi $就得到点$\omega $.点$z$在射线$OM$上，点$\omega $一定在从点$O’$出发的射线$O’M’$上，射线$O’M’$与$u$轴的正方向的夹角为$2\varphi $（图$2.8$）.

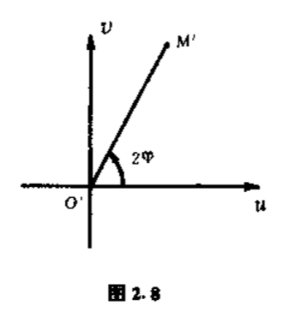
当点$z$从点$O$出发沿着$OM$跑向无穷时，点$\omega $就从点$O’$出发沿着$O’M’$跑向无穷.由此可见，函数$\omega =z^2 $把与$x$轴正向夹角为$\varphi $的射线变为与$u$轴正向夹角为$2\varphi $的射线.

现在考虑过原点$O$的两条射线$OM_1 $与$OM_2$，它们与$x$轴正向的夹角分别为$\varphi_1 $与$\varphi_2 $.不妨设$\varphi_2 \geqslant \varphi_1 $，于是$OM_1 $与$OM_2 $间的夹角为$\varphi_2 -\varphi_1 $.设函数$\omega =z^2 $把$OM_1 $变为$O’M_1’$，把$OM_2 $变为$O’M_2’$，由前面的讨论知道，它们与$u$轴正向的夹角分别为$2\varphi_1 $与$2\varphi_2 $.这样一来，$O’M_1’$与$O’M_2’$间的夹角将是$2\varphi_2 -2\varphi_1 =2(\varphi_2 -\varphi_1 )$.这就是说，在变换$\omega =z^2$之下，两直线在原点的夹角被放大成$2$倍.不难看出，交于原点的两曲线间的夹角也将放大$2$倍.于是我们得出结论：变换$\omega =z^2$在点$z=0$是不保角的.

下面我们来证明，只要$z\neq 0$，则变换$\omega =z^2$在$z_0 $就是保角的，因而原点$z_0 =0$是这个变换的唯一例外点.

任取一点$z_0 \neq 0$，并考虑过点$z_0 $的一条曲线$L$，假定在变换$\omega =z^2 $之下，曲线$L$的像曲线为$L’$，$L’$过点$\omega_0 =z_0^2$.

在曲线$L$上另取一点$z_1 \neq z_0 $，连接$z_0 $与$z_1 $得$L$的一条割线.在$L’$上有相应的一点$\omega_1 =z_1^2 $，连接$\omega_0 $与$\omega_1 $得$L’$的一条割线（图$2.9$）.

我们来比较这两条割线的方向，在曲线$L$上，向量$z_1 -z_0 $的方向就是割线的方向，在曲线$L’$上，向量$\omega_1 -\omega_0$的方向就是相应割线的方向.我们知道，向量的方向是由辐角来表示的，所以我们只需要计算$\arg{[(\omega_1 -\omega_0 )/(z_1 -z_0 )]}$.事实上，

$$\begin{align}
\arg{\dfrac{\omega_1 -\omega_0 }{z_1 -z_0 }} & =\arg{\dfrac{z_1^2 -z_0^2 }{z_1 -z_0 }} \\
& =\arg{(z_1 +z_0 )}.
\end{align}$$

可见两割线间的夹角为$\arg{(z_1 +z_0 )}$.由此我们可以进一步得到曲线$L$在$z_0 $的切线与曲线$L’$在$\omega_0 $的切线间的夹角了.让$z_1 \to z_0 $，则向量$z_1 -z_0 $的方向将趋于曲线$L$在$z_0 $的切线方向.同时，当$z_1 \to z_0 $时，$\omega_1 \to \omega_0 $，向量$\omega_1 -\omega_0 $的方向将趋于曲线$L’$在$\omega_0 $的切线方向.我们有

$$\begin{align}
\lim_{z_1 \to z_0 } \arg{\dfrac{\omega_1 -\omega_0 }{z_1 -z_0 }} & =\lim_{z_1 \to z_0 }\arg{(z_1 +z_0 )} \\
& =\arg{2z_0 } =\arg{z_0 } .
\end{align}$$

这就是曲线$L’$在$\omega_0 $的切线方向与曲线$L$在$z_0 $的切线方向的差.例如当$z_0 =1$时，$\arg{z_0 }= 0$，这说明两条切线具有相同的方向.当$z_0 =i$时，$\arg{i} =90^{\circ} $，从而两条切线互相垂直，$L’$在$\omega_0 $的切线是由$L$在$z_0 $的切线绕正向旋转$90^{\circ}$得到的.

在一般情况下，曲线$L’$在$\omega_0 $的切线方向由曲线$L$在$z_0 $的切线方向旋转一个角度$\arg{z_0 }$而得到.

现在我们不难得出，交换$\omega =z^2$在$z_0 \neq 0$的保角性了.设两条曲线$L_1 $与$L_2 $交于点$z_0 \neq 0$，并在点$z_0 $形成交角$\alpha $.再设在变换$\omega =z^2 $下，曲线$L_1 $与$L_2 $的像分别为$L_1’$与$L_2’$，它们具有交点$\omega_0 =z_0^2$.上面的讨论指出，$L_1’$在$\omega_0 $的切线方向是由$L_1 $的切线方向旋转角度$\arg{z_0} $得到的，同样的事情对于$L_2’$也成立.这样一来，$L_1’$与$L_2’$在$\omega_0 $的夹角与$L_1 $与$L_2 $在$z_0 $的夹角一样，即等于$\alpha $.这就是说，以任意一点$z_0 \neq 0$为交点的两条曲线间的夹角在变换$\omega =z^2 $下保持不变.

现在转向一般情况，我们来讨论变换

$$\omega =z^n\;(n\geqslant 2)$$

的保角性.读者不难看出，这种情况与$\omega =z^2$的情况几乎是完全一样的.

首先，$z=0$是$\omega =z^n $的保角性的例外点，在这一点变换不保角，事实上，

$$\vert \omega \vert =\vert z\vert ^n ,$$

$$\arg{\omega } =n\arg{z} .$$

借助于与$\omega =z^2$一样的讨论，我们得出结论：在变换$\omega =z^n\;(n\geqslant 2)$之下，交于原点的两曲线间的夹角被放大成$n$倍.

其次，我们证明，只要$z_0 \neq 0$，则变换$\omega =z^n $在$z_0 $就是保角的.仍考虑两条曲线$L$与$L’$，它们分别过$z_0 $与$z_0$的像点$\omega_0 =z_0^n $.为了研究曲线$L$在点$z_0 $的切线方向与曲线$L’$在点$\omega_0 $的切线方向的变化，我们在$L$上另取一点$z_1$，相应地，在$L’$上有点$\omega_1 $.然后考虑极限

$$\lim_{z_1 \to z_0 } \arg{\dfrac{\omega_1 -\omega_0 }{z_1 -z_0 }} ,$$

由读者熟知的公式

$$z_1^n -z_0^n =(z_1 -z_0 )(z_1^{n-1} +z_1^{n-2} z_0 +\cdots +z_1 z_0^{n-2} +z_0^{n-1}),$$

我们得到

$$\begin{align}
\arg{\dfrac{\omega_1 -\omega_0 }{z_1 -z_0 }} & =\arg{\dfrac{z_1^n -z_0^n }{z_1 -z_0 }} \\
& =\arg{(z_1^{n-1} +z_1^{n-2} z_0 +\cdots +z_1 z_0^{n-2} +z_0^{n-1})}.
\end{align}$$

于是，

$$\begin{align}
\lim_{z_1 \to z_0 } \arg{\dfrac{\omega_1 -\omega_0 }{z_1 -z_0 }} & =\lim_{z_1 \to z_0} \arg{(z_1^{n-1} +z_1^{n-2} z_0 +\cdots +z_1 z_0^{n-2} +z_0^{n-1})} \\
& =\arg{nz_0^{n-1}} \\
& =\arg{n} +\arg{z_0^{n-1}} \\
& =(n-1)\arg{z_0} .
\end{align}$$

这就是说，曲线$L’$在$\omega_0 $的切线方向由曲线$L$在$z_0 $的切线方向旋转一个角度$(n-1)\arg{z_0 }$而得到.运用对变换$\omega =z^2$在$z_0 \neq 0$所作的相同的讨论，我们就得到了$\omega =z^n$在$z_0 \neq 0$的保角性了.

多项式函数

我们用

$$p(z)=a_0 z^n +a_1 z^{n-1} +\cdots +a_{n-1} z+a_n \label{1.3} \tag{1.3}$$

表示复系数的多项式，这里$a_0 ,a_1 ,\cdots ,a_n $是复数.考虑由函数

$$\omega =p(z)$$

所实现的变换的保角性.根据代数基本定理，多项式$p(z)$有$n$个复根（见第五章$\S 2$）.设彼此不同的根为

$$\alpha_1 ,\alpha_2 ,\cdots ,\alpha_k \quad (k\leqslant n)$$

它们的重数分别为$l_1 ,l_2 ,\cdots ,l_k $，则

$$p(z)=(z-\alpha_1 )^{l_1 } (z-\alpha_2 )^{l_2 } \cdots (z-\alpha_k )^{l_k } .$$

现在可以研究$\omega =p(z)$的保角性了.首先指出，若根$\alpha_i $的重数$l_i \geqslant 2$，则$\alpha_i $是一个保角性的例外点.换言之，映射$\omega =p(z)$在这样的点不保角.为了证明这一点，我们任取一个根$\alpha $，并假定它的重数$l\geqslant 2$.这时$\omega =p(z)$可表示为下述形式：

$$\omega =p(z)=(z-\alpha )^l Q(z),\quad l\geqslant 2,\quad Q(\alpha )\neq 0.$$

函数$\omega =p(z)$将$z=\alpha $映为$0$.过$z=\alpha $的曲线$L$被映为过$\omega =0$的曲线$L’$.和前面一样，为了找出切线方向的变化，在$L$上另取一点$z$，并在$L’$上找出它的像点$\omega $.当$z$沿$L$趋向于$\alpha $时，向量$z-\alpha $的极限位置就是曲线$L$在点$z=\alpha $处的切线位置.同时，当$z$沿$L$趋向于$z=\alpha $时，点$\omega $就沿$L’$趋向于点$\omega =0$，向量$\omega $的极限位置就是曲线$L’$在点$\omega =0$处的切线位置，我们有下面的计算：

$$\begin{align}
\lim_{z \to \alpha } \arg{\dfrac{\omega -0 }{z -\alpha }} & =\lim_{z \to \alpha } \arg{\dfrac{(z-\alpha )^l Q(z)}{z -\alpha }} \\
& =\lim_{z\to \alpha } [(l-1)\arg{(z-\alpha )} +\arg{Q(z)}] .
\end{align}$$

现在设$L$在$z=\alpha $处的切线与$x$轴正向的夹角为$\theta $，$L’$在点$\omega =0$处的切线与$u$轴正向的夹角为$\varphi $，那么，由上面的计算可得如下结果：

$$\varphi =l\theta +\arg{Q(\alpha )} \label{1.4} \tag{1.4}$$

读者由这个结果不难得出，两条以$\alpha $为顶点的曲线间的夹角在变换$\omega =p(z)$下将被放大$l$倍.这样一来，在$p(z)$的$l\geqslant 2$级零点处，变换$\omega =p(z)$是不保角的.

由公式$\eqref{1.4}$可看出，当$l=1$时，变换$\omega =p(z)$在$z=\alpha $处是保角的.所以保角性的破坏是由于项$l\theta $的存在.我们自然会问，除了多项式$p(z)$的$l\geqslant 2$级零点外还有没有其它点破坏变换的保角性呢？如何判别一个点是不是保角性的例外点呢？

给定任意一点$z_0 $，考虑多项式

$$Q(z)=p(z)-p(z_0 ),$$

我们注意到由$\omega =Q(z)$所实现的变换与$\omega =p(z)$所实现的变换仅差一个平移.若$\omega =Q(z)$在$z_0 $是保角的，则$\omega =p(z)$在$z_0 $也是保角的，反之亦然.所以我们只要研究$\omega =Q(z)$在$z_0 $的保角性就可以了.$Q(z)$仍是一个多项式，并且$z_0 $是它的一个零点，不妨设$z_0 $是$Q(z)$的$l$级零点.于是我们有

$$Q(z)=(z-z_0 )^l Q_1 (z),\quad Q_1 (z_0 )\neq 0.$$

由前面讨论，当$l\geqslant 2$时，$\omega =Q(z)$在$z_0 $是不保角的；当$l=1$时，$\omega =Q(z)$在$z_0 $是保角的.

从上面的讨论我们知道，除了$p(z)$的$l\geqslant 2$级零点外，还可能有别的点的是保角性的例外点.但是我们仍然不清楚这样的点如何去找，它们总共有多少.为了弄清楚这些问题我们从另外的角度去考虑.

上面的讨论告诉我们，$z_0 $是变换$\omega =p(z)$的保角性的例外点的充要条件是$p(z)-p(z_0 )$有如下的分解式：

$$p(z)-p(z_0 )=(z-z_0 )^l Q_1 (z),\quad Q_1 (z_0 )\neq 0,$$

并且$l\geqslant 2$.这一条件可归结为

$$\lim_{z\to z_0 } \dfrac{p(z)-p(z_0 )}{z-z_0 } =\lim_{z\to z_0 } (z-z_0 )^{l-1} Q_1 (z) =0.$$

由$\eqref{1.3}$，

$$\begin{align}
& \dfrac{p(z)-p(z_0 )}{z-z_0 } \\
= & \dfrac{1}{z-z_0 } \times \lbrace a_0 (z^n -z_0^n ) +a_1 (z^{n-1} -z_0^{n-1} ) +\cdots +a_{n-1} (z-z_0 )\rbrace \\
= & a_0 (z^{n-1} +z^{n-2} z_0 +\cdots +zz_0^{n-2} +z_0^{n-1} ) \\
& +a_1 (z^{n-2} +z^{n-3} z_0 +\cdots +zz_0^{n-3} +z_0^{n-2} )+\cdots + a_{n-1} ,
\end{align}$$

取极限，我们有

$$\lim_{z\to z_0 } \dfrac{p(z)-p(z_0 )}{z-z_0 } =na_0 z_0^{n-1} +(n-1)a_1 z_0^{n-2} +\cdots +a_{n-1} .$$

这样一来，$z_0 $是$\omega =p(z)$的保角性的例外点的充要条件为

$$na_0 z_0^{n-1} +(n-1)a_1 z_0^{n-2} +\cdots +a_{n-1} =0.$$

我们将上式左边的多项式叫做函数$\omega =p(z)$的导函数，并记为

$$p’(z)=na_0 z^{n-1} +(n-1)a_1 z^{n-2} +\cdots +a_{n-1} .\label{1.5} \tag{1.5} $$

有了函数$\omega =p(z)$，我们不难立刻求出它的导函数.例如，若$\omega =z^3$，则$\omega’ =3z^2$；如果$\omega =4z^2+6$，则$\omega’ =8z$等等.

总结上面的讨论，我们有如下的定理：

定理$\quad $设$\omega =p(z)$，$p(z)$是由$\eqref{1.3}$给出的$n$次多项式，那么，由函数$\omega =p(z)$所实现的变换在复平面上的每一点$z$都是保角的，但最多除去$(n-1)$个例外值，这些值是由$\eqref{1.5}$式表示的$p’(z)$的根.

例$\quad $设$\omega =\dfrac13 z^3 -z$.求函数$\omega $破坏保角性的例外点.

解$\quad $只需求出导函数：

$$\omega’ =\left( \dfrac13 z^3 -z\right)’ =z^2-1 .$$

当$z=\pm 1$时，$\omega’=0$.$z=\pm 1$就是函数$\omega $的破坏保角性的例外点.

上面的定理告诉我们，$p(z)$的导函数的零点都是$\omega =p(z)$所实现的变换的保角性的例外点.这个结论可以推广到比多项式更一般的函数类中去.设$\omega =f(z)$是一个更一般的函数，定义于某一复区域$D$，设$z_0 \in D$，并假定下述极限存在：

$$\lim_{z\to z_0 } \dfrac{f(z)-f(z_0 )}{z-z_0 } .$$

由上面的证明可看出，使这个极限取零的点$z_0 $就是保角性的例外点.