地图制作

保角变换有着广泛的应用，其中一个重要方面就是将它应用于制图学上.

绘制地图就是将地球表面的一部分表示在一张平面上.表示方法自然是多种多样的，所以我们应当首先弄清楚，什么样的地图才算是一张完善的地图，有了一个标准，我们就可以来改善自己的方法，使之尽量完善.

一张完善的地图应当具备下面的两个条件：

$(1)$所有的线段都按同样的比例伸缩，

$(2)$所有的角度都保持不变.

提出这样两个要求是很自然的.当我们去旅行，或到某地出差时，自然希望手头有一张可供使用的地图.地图指给我们的方位是正确的，指给我们的距离是准确的.因而方向与距离是构成一张完善地图的两个基本要素.

从数学上来看，绘制一张地图就是建立一个从球面到平面的映射或变换，这个映射是一一的，并保持所有的角度和长度（或者长度的比例）不变.这可能吗？或者说，这样的映射存在吗？生活经验告诉我们，这的确值得怀疑，请找一块乒乓球皮，试着把它展开到平面上，既不允许把它撕开，也不允许把它折叠，你会发现，这是不可能的.这个经验告诉我们：从球面到平面的既保持角度又保持长度的一一映射是不存在的.下面我们给一个证明.

假定这样的映射是可能的.设$p$、$q$是球面上的两个不同点，$L$是球面上任意一条连接$p$和$q$的线段.再令$p’$、$q’$和$L’$是在这个映射下$p$、$q$和$L$在平面上的像.由于映射保持长度，所以$L$和$L’$等长.如果$L$是球面上的短程线，即它的长度小于球面上任何其它连接$p$和$q$的线段的长度，那么$L’$也必然短于在平面上连接$p’$和$q’$的任何其它线段的长度.我们知道，平面上的短程线是直线段，而球面上的短程线是大圆弧，由此得出结论：球面上的大圆弧必然映为平面上的直线段.特别地，由大圆弧组成的球面三角形的各边必然映为平面上直线段组成的平常的三角形的各边.

另一方面，根据映射的保角性，球面三角形的各个角必等于平面上相应三角形的内角，但是在平面上三角形的内角和是$180^{\circ}$，而球面三角形的内角和是大于$180^{\circ}$的.这样一来，从球面到平面的完善映射是不存在的.如果读者对于球面三角形的内角和大于$180^{\circ}$这一事实不知道的话，也不难从一类特例中看出.球面的每条经线都通过北极，并且与赤道垂直，即与赤道交成直角，于是在由两条连线北极与赤道的经线段和赤道组成的球面三角形中，两底角的和是$180^{\circ}$，所以整个球面三角形的内角和显然大于$180^{\circ}$.

其实早在$18$世纪之前人们可能已经从直观上清楚了不能把球面如实的映射到平面上，$18$世纪数学家们的工作揭示了，只有在柱面、锥面等所谓可展曲面才能有这样的映射.并且证明了，如果从球面到平面的映射能保持原来的长度，则将能保持所有的几何性质；主要地，不能同时保持长度和角度.人们只能舍弃长度，而保持角度.因为方向对，距离差一点不要紧；而方向不对，就走不到目的地.所以人们便把注意力集中到保持角度的映射上去了.

球极投影

$(1)$球极投影

在第一章我们已经指出，一个点列$z_1 ,z_2 ,\cdots ,z_n ,\cdots $，以$\infty $为极限就是当$n$充分大时，所有的点都落在以原点为圆心，足够大数为半径的圆外.对此我们给一个简单的几何解释.考虑一个半径为$1$，中心在原点的球面$S$，它在三维空间的方程为

$$x_1^2 +x_2^2 +x_3^2 =1,\label{2.1} \tag{2.1} $$

点$(0,0,1)$称为北极，记作$N$.$Ox_1 x_2 $平面是复平面$\mathbb{C}$.复平面与球面$S$交于赤道（图$2.10$）.

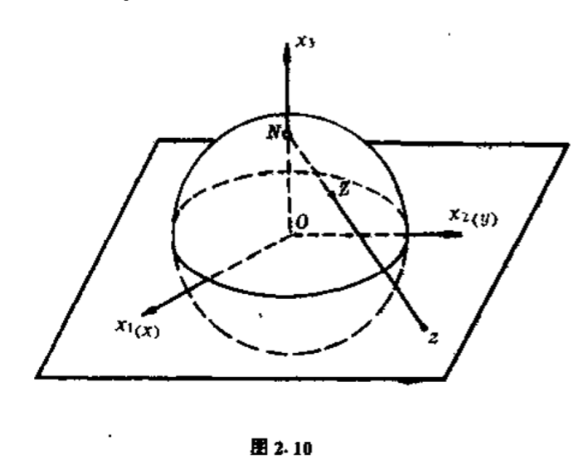
现在我们用球面上的点来表示复数$z$.为此，将点$z$用直线与北极$N$连接起来，并交球面$S$于点$Z$.当$\vert z\vert < 1$时，$Z$在下半球面上；当$\vert z\vert > 1$时，$Z$在上半球面上；当$\vert z\vert =1$，则$Z=z$.这样一来，每个复数可由球面上的一个点来表示.反过来，球面上的任一点$Z\neq N$，$Z$与$N$连线也只与复平面$\mathbb{C}$交于一点$z$.除了北极$N=(0,0,1)$外，这种对应是一一的.当$\vert z\vert \to \infty $时，$Z$趋向于$N$.因此，很自然在复平面$\mathbb{C}$上引进一个理想点，称为无穷远点，与点$N$相对应，这个点记作$\infty $.加上无穷远点复平面称为扩充的复平面，记作$\mathbb{C}_{\infty }$.$\mathbb{C}_{\infty }$与球面$S$的点建立起来的一一对应关系称为球极投影.

这样，在复平面上我们承认有唯一的无穷远点.对于无穷远点，其模是$+\infty $，而辐角是不定的.在扩充复平面上，任何一条直线都通过无穷远点.

变换公式$\quad $下面我们根据球极投影的几何构造，来推导变换公式.

设$z=x+iy$是复平面$\mathbb{C}$上的点，它的空间坐标是$(x,y,0)$，它在球面$S$上的对应点是$Z=(x_1 ,x_2 ,x_3 )$.注意到点$(0,0,1)$，$(x_1 ,x_2 ,x_3 )$，$(x,y,0)$在一条直线上，从而

$$\dfrac{x_1 -0}{x-0} =\dfrac{x_2 -0}{y-0} =\dfrac{x_3 -0}{0-1} =1-x_3 ,\label{2.2} \tag{2.2} $$

由此立刻得到

$$x=\dfrac{x_1 }{1-x_3 } ,y=\dfrac{x_2 }{1-x_3 } ,z=\dfrac{x_1 +ix_2 }{1-x_3 } ,\label{2.3} \tag{2.3} $$

公式$\eqref{2.3}$给出了用球面上对应点的坐标来表示复平面$\mathbb{C}$上的点坐标的式子.

为了得到上面公式的逆，我们注意到，

$$\begin{align}
x^2+y^2 & =\dfrac{x_1^2}{(1-x_3 )^2} +\dfrac{x_2^2 }{(1-x_3 )^2} \\
& =\dfrac{x_1^2 +x_2^2 }{(1-x_3 )^2} =\dfrac{1-x_3^2 }{(1-x_3 )^2} =\dfrac{1+x_3 }{1-x_3 } ,
\end{align}$$

由此求出

$$x_3 =\dfrac{x^2 +y^2 -1}{x^2+y^2 +1} ,\label{2.4} \tag{2.4} $$

进而，由式$\eqref{2.3}$可得出

$$x_1 =x(1-x_3 ),x_2 =y(1-x_3 ),\label{2.5} \tag{2.5} $$

把式$\eqref{2.4}$代入式$\eqref{2.5}$，可得

$$x_1 =\dfrac{2x}{x^2+y^2+1} ,x_2 =\dfrac{2y}{x^2+y^2+1} .\label{2.6} \tag{2.6} $$

重要性质$\quad $现在利用上述公式来证明球极投影的一个重要性质：

命题$\quad $在球极投影变换下，复平面$\mathbb{C}$上任何一个圆周都变成球面$S$上的圆周；反过来，任何一个球面$S$上的圆周都变成复平面$\mathbb{C}$上的一个圆周.

这里值得注意的是，“圆周”一词应当作广义的理解：直线算作半径无穷大的圆周.

证明$\quad $先证，在球极投影变换下，平面$\mathbb{C}$上的任何一个圆周都变成球面$S$上的一个圆周.事实上，在$xy$平面上任一圆周的方程具有形式

$$A(x^2 +y^2 )+Bx+Cy+D=0,\label{2.7} \tag{2.7} $$

其中$A$、$B$、$C$、$D$都是实数.当$A=0$时，方程$\eqref{2.7}$表示一条直线.将式$\eqref{2.3}$代入式$\eqref{2.7}$，不难得到

$$A\dfrac{x_3 +1}{1-x_3 } +B\dfrac{x_1 }{1-x_3 } +C\dfrac{x_2 }{1-x_3 } +D=0$$

或

$$Bx_1 +Cx_2 +(A-D)x_3 +A+D=0.\label{2.8} \tag{2.8} $$

这个方程是一次的，它表示一个平面.注意到点$(x_1 ,x_2 ,x_3 )$在球面$S$上，从面j这是平面与球面的交线，它是球面$S$上的一个圆周.

下面证明，在球极投影变换下，任何一个球面$S$上的圆周都变成平面$\mathbb{C}$上的一个圆周.

我们知道，球面$S$上的圆周都是某平面与球面$S$的交线.利用系数的任意性，总可以把一张平面表示成式$\eqref{2.8}$的形式.在球极投影变换下，这个圆周在$xy$平面上的像具有方程$\eqref{2.7}$，这是复平面$\mathbb{C}$上的圆.当$A=0$时，平面$\eqref{2.8}$过北极$N(0,0,1)$.所以只有球面上的圆周通过北极的情况下，这个圆周才变成直线.从几何上看，这个事实是明显的，因为与平面上的直线相应的球面$S$上的圆周必须经过平面上无穷远点的像点$N$.

$(2)$保角性

球极投影的另一重要性质是：保角性.具体而言，让我们在球面$S$上考虑相交某一点$M$的两条球面曲线，并假定这两条球面曲线的交角为$\alpha $，即这两条曲线在点$M$的切线的交角为$\alpha $（图$2.11$）.

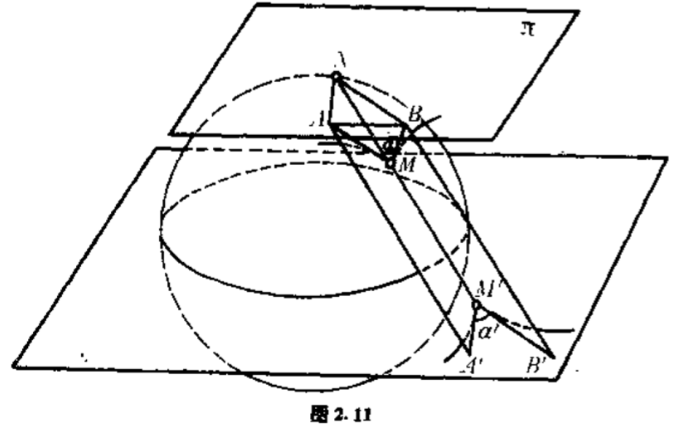
设点$M$在复平面$\mathbb{C}$上的球极投影为$M’$，两条曲线的球极投影在$M’$的切线构成某一交角$\alpha’$，我们来证明$\alpha =\alpha’$.即球极投影保持角度不变.为此，我们首先注意到，当曲线的割线趋向于曲线的切线时，割线的投影也就趋向于切线的投影，而同时也趋向于这条曲线的投影的切线.由此可见，球面$S$上两条曲线的切线的投影就是复平面$\mathbb{C}$上两条投影曲线的切线.

设球面$S$在点$N$的切平面为$\pi $.显然切平面$\pi $平行于复平面$\mathbb{C}$.现在让我们延长两条球面曲线的切线，使它们与切平面$\pi $交于点$A$和$B$.易见$\triangle ANB \cong \triangle AMB$，这是因为$AB$是两个三角形的公共边，$AN$与$AM$是从同一点出发的两条球面的切线，所以$AN=AM$，同理，$BN=BM$.因此，$\angle ANB=\angle AMB=\alpha $.现在看投影曲线的切线，其中一条是平面$NAM$与复平面$\mathbb{C}$的交线，另一条是平面$NBM$与复平面$\mathbb{C}$的交线，它们各与$AN$与$BN$平行.从而它们的交角$\alpha’$等于$\angle ANB=\alpha $.这就是我们要证明的.

$(3)$地图绘制

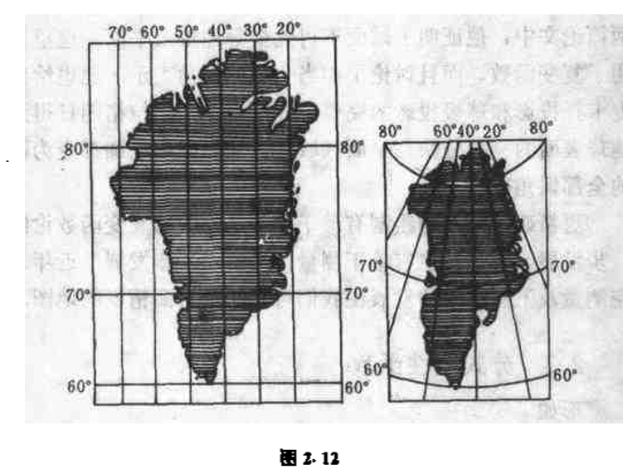
球极投影为我们提供了一种绘制地图的方法.以这种方式给出的地图保持各个方向的交角不变，但是不能保持长度的比例不变.图$2.12(a)$是在球极投影下格陵兰的地图.

利用球极投影绘制地图在历史上出现得很早.托勒密（Claudius Ptolemy，$90-168$）在他的“平球法”中用了球极平面投影.他还发明了一种锥面投影法，就是把地面上的一块区域从地心投射到一个与球面相切的锥面上.

图$2.12(a)$是借助公式

$$z’=\log \vert z\vert +i\arg{z} $$

由图$2.12(b)$得出的.这种投影法称为麦卡托投影，是荷兰科学家麦卡托（Mercator，$1512-1594$）发明的，在这张图上纬线和经线是直线.经线是等距的，但纬线的间隔是递增的，使之保持经度一分和纬度一分的长的比值.这种地图的优点之一是，地图上相互两点的罗盘方位是正确的.

兰伯特（J.H.Lambert，$1728-1777$）在理论制图学方面开创了一个新纪元.他对球面到平面的保角映射作了相当一般性的研究，并得到了这种映射的公式.欧拉（Leonhard Euler，$1707-1783$）在这方面也做出了许多贡献，而且实际上还画了一幅俄国地图，在$1775$年提出的两篇论文中，他证明了球面不可能全等地映入平面.这里他使用了复变函数，而且讨论了相当一般的保角表示.他也给出了麦卡托投影和球极投影的完整的分析.$1779$年拉格朗日（Joseph-Louis Lagrange ，$1736-1813$）得到了地球表面的一部分映到平面区域并且把纬圆和经圆都变为圆弧的全部保角变换.

更精确的地图的绘制有赖于微分几何学与复变函数论的进一步发展，自然地也有赖于测量仪器的进一步发展.近年来航空测量及卫星测量的发展使我们可以绘制出高精度的地图.

分式线性函数

形如

$$\omega =\dfrac{az+b}{cz+d} \label{2.9} \tag{2.9}$$

的函数称为分式线性函数，其中$a$、$b$、$c$、$d$是固定的复数，并且$ad-bc\neq 0$，这是因为否则线性函数$\eqref{2.9}$就与$z$无关了.

当$ad-bc=0$的时候这个表达式（莫比乌斯变换）退化成一个常数.

反过来，$z$也可以用$\omega $表示出来：

$$z=\dfrac{d\omega -b}{-c\omega +a} .$$

因而由函数$\eqref{2.9}$所决定的对应关系是双方单值的.点$z=-d/c$对应于$\omega $平面上的无穷远点，而点$\omega =a/c$对应于$z$平面上的无穷远点.

$(1)$分解

函数$\eqref{2.9}$是一个非常重要的、非常有用的函数，它有许多奇妙的性质，这使得它在近代函数论中变成一个非常基本的工具.本书只能涉及它的一些最简单的性质及应用.为此，我们把它分解为更基本的变换.直接作除法，得

$$\omega =\dfrac{az+b}{cz+d} =\dfrac{a}{c} +\dfrac{bc-ad}{c^2} \cdot \dfrac{1}{z+\dfrac{d}{c}} .\label{2.10} \tag{2.10} $$

当$c=0$时，式$\eqref{2.10}$退化为线性函数，我们在前面已经研究过了，故可设$c\neq 0$.令

$$z_1 =z+\dfrac{d}{c} ,$$

这是一个平移，再令

$$z_2 =\dfrac{1}{z_1} ,$$

则

$$\omega =\dfrac{a}{c} +\dfrac{bc-da}{c^2} \cdot z_2 .$$

利用前面对线性函数的研究，我们可将分式线性变换$\eqref{2.9}$分解为下述四种基本变换：

$(1)$ $\omega =z+a$，

$(2)$ $\omega =e^{i\theta } z$，$\theta $为实数，

$(3)$ $\omega =rz$，$r > 0$.

$(4)$ $\omega =\dfrac{1}{z} $.

$(2)$倒数变换的保角性

前三种变换我们已经清楚，今看$\omega =\dfrac{1}{z}$.令

$$z_1 =\overline{z} ,\label{2.11} \tag{2.11}$$

则

$$\omega =\dfrac{1}{\overline{z}_1 } .\label{2.12} \tag{2.12} $$

设$z=r(\cos{\theta } +i\sin{\theta } )$，则$z_1 =r(\cos{\theta } -i\sin{\theta } )$，这个映射是关于实轴的对称：模相等，而辐角差一负号，即角度改变了方向.这是反向保角的，我们称它为第二类的保角变换.

下面看$\omega =\dfrac{1}{\overline{z}_1 }$.设$\omega =\rho (\cos{\varphi } +i\sin{\varphi } )$，$z_1 =r(\cos{\theta’ } +i\sin{\theta’ } )$，那么，我们立刻有

$$\rho =\dfrac{1}{r} ,\varphi =\theta’ .$$

这个变换使辐角保持不变，而模变为倒数.设$C$表示以原点为圆心以$1$为半径的圆.这个变换把圆内的点变到圆外，点$\omega $在$Oz_1 $的连线上，它们模的乘积等于$1$.这个变换称为关于圆$C$的反演（图$2.13$）.

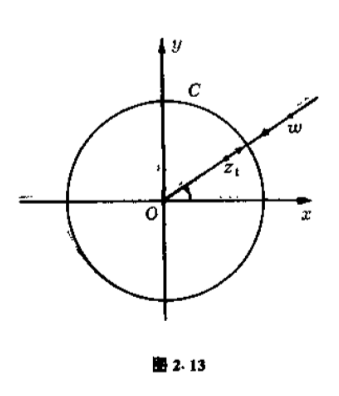
我们把点$z_1 $与$\omega $称为关于圆$C$互相对称.当$z_1 \to c$时，$\omega \to c$，当$z_1 \to 0$时，$\omega \to \infty $.这个变换改变了角度的方向，也是第二类的保角变换.

变换$z_1 =\overline{z}$与$\omega =1/\overline{z}_1$复合起来就得到原来的变换$\omega =1/z$，它是保角的.实际上我们可以利用本章$\S 1$中关于保角性的讨论直接讨论极限

$$\lim_{z\to z_0 } \dfrac{\omega -\omega_0 }{z-z_0 } ,$$

看它是否为零.事实上，

$$\lim_{z\to z_0 } \dfrac{\omega -\omega_0 }{z-z_0 } =\lim_{z\to z_0 } \dfrac{\dfrac{1}{z} -\dfrac{1}{z_0 }}{z-z_0 } =\lim_{z\to z_0 } -\dfrac{1}{zz_0 } =-\dfrac{1}{z^2} .$$

当$z_0 \neq 0$时，这个极限不可能取零值，所以由函数$\omega =\dfrac{1}{z} $所确定的映射在$z\neq 0$处是保角的.

由此，将四种基本变换复合起来就得出分式线性变换的保角性.读者也不难借助求极限直接证明之.

$(3)$保圆性

分式线性变换的另一个重要性质是它的保圆性，即圆在分式线性变换下的像仍是圆.不过与$2.2.2$节一样，我们需要对于圆的理解加以推广，这里的圆包括直线，直线理解为半径为无穷大的圆.这样一来，在分式线性变换下，直线或圆的像仍是直线或圆.

由于分式线性变换可分解为$(1)\;\omega =az+b$与$(2)\; \omega =\dfrac{1}{z} $的复合，所以只要证明这一性质对$(1)$与$(2)$成立就可以了.圆周的方程可以写为

$$A(x^2+y^2)+mx+ny+l=0.\label{2.13} \tag{2.13} $$

当$A=0$时，方程$\eqref{2.13}$表示直线.方程$\eqref{2.13}$可以写成复形式：

$$Az\overline{z} +\overline{B} z+B\overline{z} +C=0,\label{2.14} \tag{2.14} $$

其中$A$、$C$都是实常数.

代换$x^2+y^2=z\overline{z} $，$x=\dfrac{z+\overline{z}}{2} $，$y=\dfrac{z-\overline{z}}{2i} $，

则得到圆方程的复数形式

$$Az\overline{z} +\overline{B} z+B\overline{z} +C=0,$$

其中$A,C$为实常数，$B=\dfrac{1}{2} (m+in)$为复常数.

$\omega =az+b$的保圆性前面已经讨论过，因而现在只需讨论变换$\omega =1/z$的保圆性.把$\omega =\dfrac{1}{z}$代入$\eqref{2.14}$得

$$A\dfrac{1}{\omega \overline{\omega } } +\dfrac{\overline{B}}{\omega } +\dfrac{B}{\overline{\omega } } +C=0,$$

去掉分母得

$$A+\overline{B\omega } +B\omega +C\omega \overline{\omega } =0.\label{2.15} \tag{2.15} $$

方程$\eqref{2.15}$在$\omega $平面上仍然代表圆周，当$C=0$时，它表示一条直线.

这样，我们看到了，分式线性变换保持圆周不变.

儒可夫斯基截线

$(1)$三个基本映射

本章开头提到了机翼断面的保角映射问题，现在就来具体解决这一问题.下面我们讨论几个简单函数所实现的保角映射，这些映射无论在理论上还是应用中都是很有用的.这些映射是：

$(1)$ $t=\dfrac{z-a}{z-b} $，

$(2)$ $z’=z^2$，

$(3)$ $\omega =\dfrac12 \left( z+\dfrac{1}{z} \right) $.

最后一个函数叫做儒可夫斯基函数，我们在第一章已经见过了.它是以俄国科学家儒可夫斯基（Zhukovsky，$1847-1921$）命名的，因为儒可夫斯基成功地将这个函数应用到机翼理论的研究中.

$(2)$儒可夫斯基映射

考虑圆弧$l$，它与实轴的交点是$-a$和$a$，与虚轴的交点为$hi$，$h > 0$.求将沿圆弧$l$有裂缝的$z$平面映射为$\omega $平面上中心在点$hi$且通过$-a$和$a$的圆$G$的外部的映射（图$2.14$）.

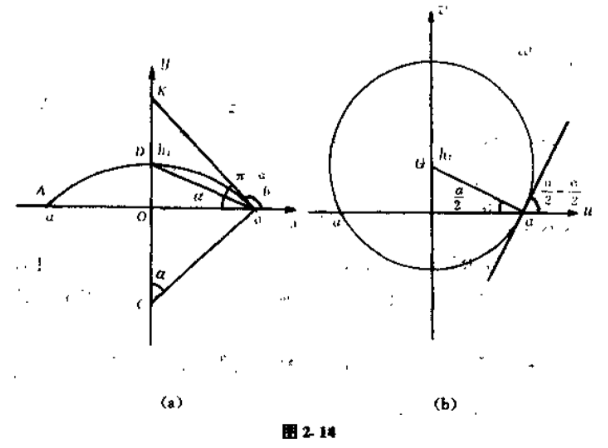
为了找到这个映射，需要先弄清楚有裂缝$l$的平面的几何结构.如图$2.14(a)$所示.设$A$、$B$、$D$是数$-a$、$a$、$hi$的对应点，$C$是圆弧所在圆的中心，并设在点$B$处圆弧$l$的切线$BK$与实轴负方向的夹角为$\alpha$.我们来证明，$DB$与实轴负方向的夹角为$\dfrac{\alpha }{2}$.事实上，

$\triangle KBO$是直角三角形，从而$\angle OKB+\alpha =\dfrac{\pi}{2}$；

$\triangle KBC$是直角三角形，从而$\angle OKB+\angle OCB =\dfrac{\pi }{2} $；

由此可知，$\angle OCB=\alpha $.这个角是弦$BD$所对的中心角.而$\angle KBD$是弦$BD$所对的弦切角.根据初等几何学的定理，$\angle KBD=\dfrac{\alpha }{2}$.从而

$$\angle OBD=\dfrac{\alpha }{2} ,$$

现在看$\omega $平面（图$2.14(b)$）.在$\omega $平面上由点$hi$到点$a$的半径与实轴负方向所夹的角也是$\dfrac{\alpha }{2}$，而在点$a$处圆周的切线与实轴正方向间的夹角等于$\dfrac{\pi }{2} -\dfrac{\alpha }{2}$.要想求出能实现所要求的映射的函数，需先将沿弧$l$有裂缝的$z$平面和$\omega $平面上圆$G$的外部映射到同一个辅助区域.

$(3)$变换的实现

为此，考虑函数

$$t=\dfrac{z-a}{z+a} ,$$

它将沿弧$l$有裂缝的$z$平面映射为沿一条射线有裂缝的$t$平面（图$2.15$）.

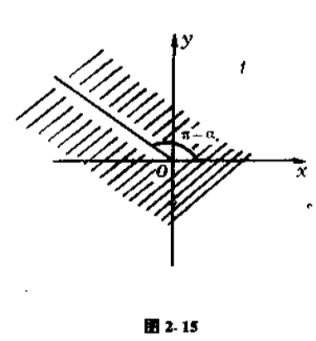
事实上，这是一个分式线性变换，它有保圆性.它将$a$映射到$O$，将$-a$映到$\infty $，从而将过$a$与$-a$的圆弧映为过$O$与$\infty $的射线.当$z$沿实轴由$a$向右移动时，点$t$也沿实轴由$O$向右移动.这样函数$t$把$z$平面上沿实轴$z > a$的部分映为$t$平面上的正实轴.由映射的保角性可推得，$l$在$t$平面上的像，即那条射线，与正实轴的夹角为$\pi -\alpha $.

再考虑另一个辅助函数

$$T=\dfrac{\omega -a}{\omega +a} .$$

它将$\omega $平面上已给圆周映射为$T$平面上通过原点的直线（图$2.16$）.

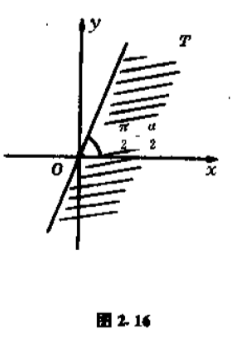
$\omega $平面的实轴映为$T$平面的实轴，并且当点$\omega $沿实轴由点$a$向右移动时，点$T$也沿实轴由原点向右移动.由此可知，$\omega $平面上圆$G$的外部映射为包含正实轴的半个$T$平面，它的边界线与正实轴的交角为$\dfrac{\pi }{2} -\dfrac{\alpha }{2} $，即$\omega $平面上已给圆周在点$a$处切线的斜角.

不难看出，函数

$$t=T^2$$

将半个$T$平面映射为沿与实轴正向夹角为$2\left( \dfrac{\pi }{2} -\dfrac{\alpha }{2} \right) =\pi -\alpha $的射线有裂缝的$t$平面.

这样一来，将沿弧$l$有裂缝的平面映为圆$G$外的函数由等式

$$\left( \dfrac{\omega -a}{\omega +a} \right)^2 =\dfrac{z-a}{z+a} $$

而确定.解此方程，得

$$z=\dfrac12 \left( \omega +\dfrac{a^2}{\omega } \right) ,$$

或

$$\omega =z+\sqrt{z^2-a^2} .$$

因为所得关系式不含$h$，所以以连接点$-a$和$a$的任何圆弧为裂缝的$z$平面都映为通过点$-a$与$a$的圆周的外部，这个圆的中心与已给弧和虚轴的交点相重合（如果把$z$平面和$\omega $平面看做同一个的话）.

$\omega $平面上包含圆$G$且与圆$G$切于点$a$的任何圆的外部，借助于刚才所求得的函数，映射为包含弧$l$的某条闭曲线的外部.这条闭曲线在点$a$处有尖点，尖点处的切线与弧$l$在该点的切线相重合（图$2.17$）.

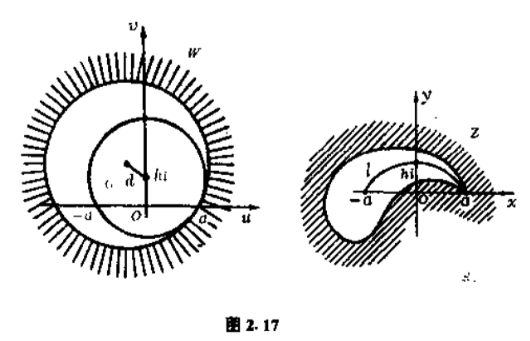
这种闭曲线叫做儒可夫斯截线.儒可夫斯基截线的形状依赖于参数$a$和$h$，也依赖于两个圆中心的距离$d$.

由于将儒可夫斯基截线的外部映射为圆的外部的函数具有非常简单和形式，这就使得在计算绕儒可夫斯基类型的机翼的环流时变得非常方便.