多项式的泰勒公式

若$p(x)$是$n$次整多项式：

$$p(x)=a_0 +a_1 x+a_2 x^2 +a_3 x^3 +\cdots +a_n x^n ,\label{1} \tag{1} $$

则逐次将它微分$n$次：

$$\begin{array}{l}
p’(x) =a_1 +2\cdot a_2 x+3\cdot a_3 x^2 +\cdots +n \cdot a_n x^{n-1} ,\\
p’’(x) =1\cdot 2\cdot a_2 +2\cdot 3\cdot a_3 x+\cdots +(n-1)n\cdot a_n x^{n-2} ,\\
p’’’ (x) =1\cdot 2\cdot 3\cdot a_3 +\cdots +(n-2)(n-1)n\cdot a_n x^{n-3} ,\\
\cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \\
p^{(n)} (x)=1\cdot 2\cdot 3\cdots n\cdot a_n \end{array}$$

并且在一切这些式子内令$x=0$，就得出用多项式本身及其导数在$x=0$时的数值去表达这多项式的系数的式子：

$$a_0 =p(0) ,a_1 =\dfrac{p’(0)}{1!} ,a_2 =\dfrac{p’’(0)}{2!} ,a_3 =\dfrac{p’’’(0)}{3!} ,\cdots ,a_n =\dfrac{p^{(n)}(0)}{n!} .$$

把这些系数的数值代入$\eqref{1}$：

$$p(x)=p(0)+\dfrac{p’(0)}{1!} x+\dfrac{p’’(0)}{2!} x^2 +\dfrac{p’’’(0)}{3!} x^3 +\cdots +\dfrac{p^{(n)}(0)}{n!} x^n .\label{2} \tag{2}$$

这公式与$\eqref{1}$的区别只在于系数的写法不同.

可以用它依$(x-x_0 )$的幂展开

$$p(x)=A_0 +A_1 (x-x_0 )+A_2 (x-x_0 )^2 +A_3 (x-x_0 )^3 +\cdots +A_n (x-x_0 )^n \label{3} \tag{3}$$

来代替它依$x$的幂展开的多项式，这里的$x_0 $是$x$的某一特殊常数值.令$x-x_0 =\xi $，$p(x)=p(x_0 +\xi )=P(\xi )$，对于多项式

$$P(\xi )=A_0 +A_1 \xi +A_2 \xi^2 +A_3 \xi^3 +\cdots +A_n \xi^n $$

的系数，依已证明的式子，可得：

$$A_0 =P(0),A_1 =\dfrac{P’(0)}{1!} ,A_2 =\dfrac{P’’(0)}{2!} ,A_3 =\dfrac{P’’’(0)}{3!} ,\cdots ,A_n =\dfrac{P^{(n)} (0)}{n!} .$$

但

$$P(\xi )=p(x_0 +\xi ),P’(\xi )=p’(x_0 +\xi ),P’’(\xi )=p’’(x_0 +\xi ),\cdots ,$$

于是

$$P(0)=p(x_0 ) ,P’(0)=p’(x_0 ),P’’(0)=p’’(x_0 ),\cdots $$

而

$$A_0 =p(x_0 ),A_1 =\dfrac{p’(x_0)}{1!} ,A_2 =\dfrac{p’’(x_0)}{2!} ,A_3 =\dfrac{p’’’(x_0)}{3!} ,\cdots ,A_n =\dfrac{p^{(n)} (x_0)}{n!} ,\label{4} \tag{4} $$

就是说，展开式$\eqref{3}$的系数可用多项式本身及其导数在$x=x_0 $时的数值来表达.

把表达式$\eqref{4}$代入$\eqref{3}$：

$$p(x)=p(x_0 )+\dfrac{p’(x_0)}{1!} (x-x_0 )+\dfrac{p’’(x_0)}{2!} (x-x_0 )^2 +\dfrac{p’’’(x_0)}{3!} (x-x_0 )^3 +\cdots +\dfrac{p^{(n)} (x_0)}{n!} (x-x_0 )^n .\label{5} \tag{5} $$

公式$\eqref{5}$以及它的特别情形（在$x_0 =0$时）$\eqref{2}$都称为泰勒（B.Taylor）公式.它在代数上有什么重要的用处，这是大家都知道的.

我们作一条（对以后有用处的）明显的附注，若多项式$p(x)$可表示为下面的形式

$$p(x)=c_0 +\dfrac{c_1 }{1!} (x-x_0 )+\dfrac{c_2 }{2!} (x-x_0 )^2 +\dfrac{c_3 }{3!} (x-x_0 )^3 +\cdots +\dfrac{c_n }{n!} (x-x_0 )^n ,$$

则必有

$$p(x_0 )=c_0 ,p’(x_0 )=c_1 ,p’’(x_0 )=c_2 ,\cdots ,p^{(n)}(x_0 )=c_n .$$

任意函数的展开式$\cdot $余项的佩亚诺式

今转而考察一般并不是多项式的任意函数$f(x)$.假定它在某一点$x_0 $处存在着直至$n$阶为止的各阶导数.准确些说，这意思是说，函数在含有点$x_0 $的某一区间$[a,b]$内是有定义的，并且有直至$(n-1)$阶为止的各阶导数：

$$f’(x),f’’(x),\cdots ,f^{(n-1)} (x),$$

除此以外，在这点$x_0 $处还有$n$阶导数$f^{(n)} (x_0 )$.那么依$\eqref{5}$的形式，对于函数$f(x)$也可以作出多项式

$$p(x)=f(x_0 )+\dfrac{f’(x_0 ) }{1!} (x-x_0 )+\dfrac{f’’(x_0 ) }{2!} (x-x_0 )^2 +\cdots +\dfrac{f^{(n)}(x_0 ) }{n!} (x-x_0 )^n .\label{6} \tag{6}$$

根据前面一目的附注，这多项式及其导数（直至$n$阶为止）在点$x_0 $处与函数$f(x)$及其导数各有相同的数值.

但在这次，只要$f(x)$不是$n$次多项式，就已经不能肯定等式$f(x)=p(x)$.多项式$p(x)$仅给出函数$f(x)$的某一近似式.因此，研究差

$$r(x)=f(x)-p(x)\label{7} \tag{7}$$

就成为特别有趣的事情.

首先要证明，在$x\to x_0 $时这差是高于$n$阶的无穷小（与$x-x_0$比较）：

$$r(x)=o ((x-x_0)^n) .\label{8} \tag{8}$$

依多项式$p(x)$的性质，对于$r(x)$显然将成立等式

$$r(x_0 )=r’(x_0 )=r’’(x_0 )=\cdots =r^{(n)} (x_0 )=0.\label{9} \tag{9}$$

现在确立以下的一般命题：对任何函数$r(x)$，在点$x_0 $有直到$n$阶导数的，如果满足条件$\eqref{9}$，则关系式$\eqref{8}$成立.

用数学归纳法来证明.当$n=1$时，这一命题的形式是：若在点$x_0 $具有（一阶）导数的函数$r(x)$满足条件

$$r(x_0 )=r’(x_0 )=0,$$

则

$$r(x)=o(x-x_0 ).$$

这个命题就可以直接证明

$$\lim_{x\to x_0 } \dfrac{r(x)}{x-x_0 } =\lim_{x\to x_0 } \dfrac{r(x)-r(x_0 )}{x-x_0 } =r’(x_0 ) =0.$$

今假定上述命题对某一$n\geqslant 1$成立，而来证明当$n$换成$(n+1)$时命题也成立，即：若在点$x_0 $具有直到$n+1$阶导数的函数$r(x)$满足条件

$$r(x_0 )=r’(x_0 )=r’’(x_0 ) =\cdots =r^{(n)} (x_0 ) =r^{(n+1)} (x_0 ) =0\label{91} \tag{9*}$$

则

$$r(x)=o((x-x_0 )^{n+1}) .\label{81} \tag{8*}$$

自$\eqref{91}$可看出$r’(x)$满足$\eqref{9}$这种形式的条件，故依假设对$r’(x)$就有

$$r’(x)=o((x-x_0 )^n).$$

但依有限增量公式$[112]$，

$$r(x)=r(x)-r(x_0 )=r’(c)(x-x_0 ),$$

其中$c$在$x_0 $与$x$之间；故$\vert c-x_0 \vert < \vert x-x_0 \vert $，于是

$$r’(c)=o((c-x_0 )^n) =o((x-x_0 )^n),$$

我们就得到$\eqref{81}$，这就是要证明的.

于是我们的命题对任何自然数$n$是成立的，而差式$\eqref{7}$确实满足关系式$\eqref{8}$.注意$\eqref{6}$，便得公式

$$f(x)=f(x_0 )+\dfrac{f’(x_0 ) }{1!} (x-x_0 )+\dfrac{f’’(x_0 ) }{2!} (x-x_0 )^2 +\cdots +\dfrac{f^{(n)}(x_0 ) }{n!} (x-x_0 )^n +o((x-x_0 )^n) ,\label{10} \tag{10}$$

这与公式$\eqref{5}$只相差余项$\eqref{8}$.以上述形式来给出的余项的是佩亚诺（G.Peano）.公式$\eqref{10}$也称为带有佩亚诺式余项的泰勒公式.

已证明的公式是$96$公式$(3)$的自然的推广，该式可以写成：

$$f(x)=f(x_0 )+f’(x_0 )(x-x_0 )+o(x-x_0 );$$

它对应于$n=1$.在那里除了高于一阶无穷小的误差以外，函数$f(x)$可以表示为线性函数的形式，在这里除了高于$n$阶无穷小的误差以外，我们同样可以把$f(x)$表示为$n$次多项式的形式.

很易指出，函数$f(x)$的这种表示式是唯一的，即若在$x_0$的近外同时有

$$f(x)=A_0 +A_1 (x-x_0 )+A_2 (x-x_0 )^2 +\cdots +A_n (x-x_0 )^n +o((x-x_0 )^n) $$

及

$$f(x)=A_0’ +A_1’ (x-x_0 )+A_2’ (x-x_0 )^2 +\cdots +A_n’ (x-x_0 )^n +o((x-x_0 )^n) ,$$

事实上，由恒等式

$$\begin{align}
& A_0 +A_1 (x-x_0 )+A_2 (x-x_0 )^2 +\cdots +A_n (x-x_0 )^n \\
= & A_0’ +A_1’ (x-x_0 )+A_2’ (x-x_0 )^2 +\cdots +A_n’ (x-x_0 )^n +o((x-x_0 )^n) \end{align}$$

在$x\to x_0 $时立刻得出$A_0 =A_0’$.约去这两项，并用$x-x_0 $除它们，得出：

$$\begin{align}
& A_1 +A_2 (x-x_0 ) +\cdots +A_n (x-x_0 )^{n-1} \\
= & A_1’ +A_2’ (x-x_0 ) +\cdots +A_n’ (x-x_0 )^{n-1} +o((x-x_0 )^{n-1}) ,\end{align}$$

由此类似地可得$A_1 =A_1’$，余类推.

有时应用公式$\eqref{10}$的另一形式更为方便.余项$r(x)$可以表示为：

$$r(x)=\dfrac{\alpha }{n!} (x-x_0 )^n ,$$

其中$\alpha $依赖于$x$，而且随着$x-x_0$同时趋向于$0$.把这表达式代入$\eqref{10}$，就得

$$f(x)=f(x_0 )+\dfrac{f’(x_0 ) }{1!} (x-x_0 )+\dfrac{f’’(x_0 ) }{2!} (x-x_0 )^2 +\cdots +\dfrac{f^{(n)}(x_0 ) +\alpha }{n!} (x-x_0 )^n .\label{101} \tag{10a}$$

更进一步，在公式$\eqref{10}$内把$f(x_0 )$移到左边去，并且令$x-x_0 =\Delta x$，就可以将它改写成

$$\Delta f(x_0 )=f’(x_0 )\cdot \Delta x+\dfrac{1}{2!} f’’(x_0 ) \cdot \Delta x^2 +\cdots +\dfrac{1}{n!} f^{(n)} (x_0 )\cdot \Delta x^n +o(\Delta x^n).\label{102} \tag{10б}$$

在这种形式下，它就更接近于$96$的公式$(3)$：

$$\Delta f(x_0 )=f’(x_0 )\cdot \Delta x+o(\Delta x).$$

上式在函数的无穷小增量$\Delta f(x_0 )$内仅分出一个主项——这里，照常以$\Delta x$作为基本无穷小——可是在公式$\eqref{102}$内直至含$\Delta x$的$n$次幂为止的各项却都写出来了，并且它们都是在$63$的意义下最简单的无穷小.

这样，除了余项所生的误差以外，函数的增量就展开成为自变量的增量的幂了.

最后，回想起

$$f’(x_0 )\cdot \Delta x=\mathbb{d} f(x_0 ),f’’(x_0 )\cdot \Delta x^2=\mathbb{d}^2 f(x_0 ),\cdots ,f^{(n)}(x_0 )\cdot \Delta x^n=\mathbb{d}^n f(x_0 ),$$

我们可以把$\eqref{102}$改写成这样的形式：

$$\Delta f(x_0 )=\mathbb{d} f(x_0 )+\dfrac{1}{2!} \mathbb{d}^2 f(x_0 ) +\cdots +\dfrac{1}{n!} \mathbb{d}^n f(x_0 ) +o(\Delta x^n).$$

由此可见（当$\Delta x\to 0$时）在函数的无穷小增量的展开式中，除去各项分母中的阶乘因子不论，逐次的微分就表示对应项的最简单的无穷小项.

例题

若$x_0=0$，泰勒公式看来是最简单的：

$$f(x)=f(0)+\dfrac{f’(0) }{1!} x+\dfrac{f’’(0) }{2!} x^2 +\cdots +\dfrac{f^{(n)}(0)}{n!} x^n +o(x^n) .\label{11} \tag{11}$$

在取$x-x_0 $作为新的自变量之后，一般的泰勒公式总归可以化为这个特别情形的.

现在以例题的形式来考察某些初等函数依这公式的具体展开式.

$1)$设$f(x)=e^x$，则$f^{(k)} =e^x(k=1,2,\cdots )$.因为在这时$f(0)=1$，$f^{(k)} (0)=1$，故依公式$\eqref{11}$，

$$e^x =1+\dfrac{x}{1!} +\dfrac{x^2}{2!} +\cdots +\dfrac{x^n}{n!} +o(x^n).$$

$2)$若$f(x)=\sin{x}$，则$f^{(k)} (x)=\sin{\left( x+k\cdot \dfrac{\pi }{2} \right) } $，于是

$$f(0)=0,f^{(2m)} (0)=\sin{m\pi } =0,$$

$$f^{(2m-1)} (0)=\sin{\left( m\pi -\dfrac{\pi }{2} \right) } =(-1)^{m-1} \quad (m=1,2,\cdots ).$$

因此，在公式$\eqref{11}$内令$n=2m$，就有

$$\sin{x} =x-\dfrac{x^3}{3!} +\dfrac{x^5}{5!} -\cdots +(-1)^{m-1} \dfrac{x^{2m-1}}{(2m-1)!} +o(x^{2m}) .$$

$3)$类似地，在$f(x)=\cos{x}$时：

$$f^{(k)} (x) =\cos{\left( x+k\cdot \dfrac{\pi }{2} \right) } ;$$

$$f(0)=1,f^{(2m)} (0)=(-1)^m ,f^{(2m-1)} (0)=0\quad (m=1,2,\cdots ).$$

这样（若取$n=2m+1$）：

$$\cos{x} =1-\dfrac{x^2}{2!} +\dfrac{x^4}{4!} -\cdots +(-1)^m \dfrac{x^{2m}}{(2m)!} +o(x^{2m+1}) .$$

$4)$今考察幂函数$x^m $，此处$m$非自然数也非零.在这情形，当$x\to 0$时，或则函数本身（若$m < 0$），或则它的导数（从某一个$n > m$阶开始）无限地增大.因此，在此处已不能取$x_0 =0$.

取$x_0 =1$，即依$(x-1)$的幂而展开$x^m $.如前所述，我们可以把$x-1$当作新的变量，但若我们仍旧用$x$来记这新的变量，则问题就成为依$x$的幂而展开$(1+x)^m$了.

我们知道$[116,2)]$

$$f^{(k)}(x) =m(m-1)\cdots (m-k+1)(1+x)^{m-k} ,$$

因此

$$f(0)=1,f^{(k)} (0) =m(m-1)\cdots (m-k+1).$$

展开式的形式就是

$$(1+x)^m =1+mx +\dfrac{m(m-1)}{1\cdot 2} x^2 +\cdots +\dfrac{m(m-1)\cdots (m-n+1)}{1\cdot 2\cdot \cdots \cdot n} x^n +o(x^n) .$$

特别情形，例如在$n=2$及$m=-1,\dfrac12 ,-\dfrac12 $时，就有

$$\dfrac{1}{1+x} =1-x+x^2 +o(x^2) ,$$

$$\sqrt{1+x} =1+\dfrac12 m-\dfrac18 x^2 +o(x^2),$$

$$\dfrac{1}{\sqrt{1+x}} =1-\dfrac12 x+\dfrac38 x^2 +o(x^2).$$

在这些展开式中，第一式很容易由初等方法得出；此处的余项实即$\dfrac{x^3}{1+x}$.至于第二式及第三式就需要更长的计算[比较$63$].

$5)$若转而讨论对数函数$\ln x$，它在$x\to +0$时趋向于$-\infty $，所以仿照前例，我们只能考察函数$f(x)=\ln (1+x)$，并且依$x$的幂展开它.

那时$[163,3)]$

$$f^{(k)} (x)=\dfrac{(-1)^{k-1} (k-1)!}{(1+x)^k} ;$$

$$f(0)=0,f^{(k)} (0)=(-1)^{k-1} (k-1)!.$$

由此

$$\ln (1+x)=x-\dfrac{x^2}{2} +\dfrac{x^3}{3}-\cdots +(-1)^{n-1} \dfrac{x^n}{n} +o(x^n).$$

$6)$今设$f(x)=\arctan{x}$.我们在$118,4)$内已得到它的导数在$x=0$时的数值：

$$f^{(2m)} (0)=0,f^{(2m-1)} (0)=(-1)^{m-1} (2m-2)!,$$

于是它的展开式可表示为

$$\arctan{x} =x-\dfrac{x^3}{3} +\dfrac{x^5}{5} -\cdots +(-1)^{m-1} \dfrac{x^{2m-1}}{2m-1} +o(x^{2m}) .$$

$7)$对于函数$f(x)=\tan{x}$，泰勒公式的系数构成的规律是较繁复的.但要写出它的为首几项并不困难.例如，因为

$$f’(x)=\dfrac{1}{\cos{}^2 x} ,f’’(x)=\dfrac{2\sin{x}}{\cos{}^3 x} ,f’’’(x) =2\dfrac{1+2\sin{}^2 x}{\cos{}^4 x} ,$$

$$f^{\mathrm{IV}} (x)=8\sin{x} \dfrac{2+\sin{}^2 x}{\cos{}^5 x} ,$$

故

$$f(0)=0,f’(0)=1,f’’(0)=0,f’’’(0)=2,f^{\mathrm{IV}} (0)=0,$$

于是

$$\tan{x} =x+\dfrac{x^3}{3} +o(x^4) .$$

利用已知的展开式，就已经可以不用求导数而直接写出较繁复的函数的展开式.例如，前一公式就可以从$\sin{x}$及$\cos{x}$的展开式而求得.举几个新的例子，在这时一切$x$的幂直到指定的幂包括在内为止，我们都要精确地计算出来，而更高的幂（没有写出来的）自然是包括在余项内.

$8)$写出函数$e^{\sin{x}}$的展开式至$x^3$.根据$1)$，

$$e^{\sin{x}} =1+\sin{x} +\dfrac12 \sin{}^2 x+\dfrac16 \sin{}^3 x +o(x^3) ;$$

原来应该写成$o(\sin{}^3 x)$，但由于$x$与$\sin{x}$是等价无穷小，所以写成$o(x^3)$是完全一样的.

但依$2)$

$$\sin{x} =x-\dfrac16 x^3 +o(x^4),$$

于是

$$e^{\sin{x}} =1+\left( x-\dfrac16 x^3\right) +\dfrac12 x^2 +\dfrac16 x^3 +o(x^3).$$

含$x^3$的项互相消去，故最后得

$$e^{\sin{x}} =1+x+\dfrac12 x^2 +o(x^3) .$$

类似地

$$e^{\tan{x}} =1+x+\dfrac12 x^2 +\dfrac12 x^3 +o(x^3).$$

$9)$写出函数$\ln \cos{x}$的展开式至$x^6$的项.根据$5)$，

$$\ln \cos{x} =\ln [1+(\cos{x} -1)] =(\cos{x} -1) -\dfrac12 (\cos{x} -1)^2 +\dfrac13 (\cos{x} -1)^3 +o(x^6) .$$

因为$1-\cos{x}$与$x^2$同阶$[61]$，故$o((\cos{x} -1)^3)$同时就是$o(x^6)$.

在这时，由于$3)$，

$$\cos{x} -1=-\dfrac12 x^2 +\dfrac{1}{24} x^4 -\dfrac{1}{720} x^6 +o(x^7) ;$$

由此

$$\ln \cos{x} =\left( -\dfrac12 x^2 +\dfrac{1}{24} x^4 -\dfrac{1}{720} x^6 \right) -\dfrac12 \left( \dfrac14 x^4 -\dfrac{1}{24} x^6 \right) +\dfrac13 \left( -\dfrac18 x^6 \right) +o(x^6),$$

或在化简后，

$$\ln \cos{x} =-\dfrac12 x^2 -\dfrac{1}{12} x^4 -\dfrac{1}{45} x^6 +o(x^6) .$$

类似地

$$\ln (x+\sqrt{1+x^2} )=x-\dfrac16 x^3 +\dfrac{3}{40} x^5 +o(x^5) $$

而

$$\ln \dfrac{\sin{x} }{x} =-\dfrac16 x^2 -\dfrac{1}{180} x^4 -\dfrac{1}{2835} x^6 +o(x^6) .$$

一切这些不直接利用泰勒公式而得出的展开式，当然也可以由泰勒公式求得，并且由于函数的这种展开式的唯一性，也就恰好有着同样的系数.

附注$\quad $因为在这里所考察的函数在点$x=0$的邻域内都有着任何阶的导数，所以我们在公式$\eqref{11}$内对于$n$的选取不受拘束，就是可以继续展开这些函数直至$x$的任意次幂.

余项的其他形式

带有佩亚诺式余项的泰勒公式有各种各样的应用（参阅下一章）；但它们总是属于所谓“局部”性质的，即关于该点$x_0 $的性质的.若另外也讲及其他数值$x$，则这些数值就必假定是“十分接近”于$x_0 $，而不能预先任意选取的.

与此同时，自然地企图利用多项式$p(x)$作为函数$f(x)$的近似式，用了它就可以计算$f(x)$的数值至所需的准确度.

要多项式$p(x)$能胜任这一任务，就必须有可能对已给的$x$值去估计$\eqref{7}$式中的差.在这情形，佩亚诺形式的余项仅表明当$x\to 0$时$r(x)$也趋于$0$的性质，不能有什么用处.我们不能由此确定，对于怎样的$x$的数值多项式$p(x)$可以表达函数$f(x)$至预先指定的准确度；它也没有说到对于已给的$x$，由于$n$的增大，余项$r(x)=r_n (x)$的数值受到什么样的影响，等等.

因此我们转而推导余项$r_n (x)$的其他形式.为着明确起见，我们将考察在点$x_0 $右方的区间$[x_0 ,x_0 +H] (H > 0)$，并且设想函数$f(x)$是在这区间内定义着的；至于函数被给定在区间$[x_0 -H,x_0 ]$内时的情形，就可类似地加以说明了.

在这一次要作更多的假定，就是假设在全区间$[x_0 ,x_0 +H]$内前$n$个导数：

$$f’(x),f’’(x),f’’’(x),\cdots ,f^{(n)} (x)$$

都存在着而且都是连续的，此外，至少在开区间$(x_0 ,x_0 +H)$内$(n+1)$阶导数$f^{(n+1)} (x)$存在着而且是有限的.

注意，由于$\eqref{6}$及$\eqref{7}$，

$$r_n (x) =f(x)-f(x_0 )-\dfrac{f’(x_0 )}{1!} (x-x_0 )-\dfrac{f’’(x_0 )}{2!} (x-x_0 )^2-\cdots -\dfrac{f^{(n)}(x_0 )}{n!} (x-x_0 )^n .\label{12} \tag{12}$$

今将$x$固定于区间$[x_0 ,x_0 +H]$内的任一数值，并且依照公式$\eqref{12}$右端的式样，把常数$x_0 $换成变量$z$，做一个新的辅助函数：

$$\varphi (z) =f(x)-f(z )-\dfrac{f’(z )}{1!} (x-z )-\dfrac{f’’(z )}{2!} (x-z )^2-\cdots -\dfrac{f^{(n)}(z )}{n!} (x-z )^n ,$$

其中自变量$z$算作是在区间$[x_0 ,x]$内变动的.在这区间内，函数$\varphi (z)$是连续的，并且在它的端点处取得数值[参阅$(12)$]：

$$\varphi (x_0 )=r_n (x),\varphi (x)=0.$$

此外，在区间$(x_0 ,x)$内存在着导数

$$\begin{align}
\varphi’ (z) = & -f’(z)-\left[ \dfrac{f’’(z)}{1!} (x-z)-f’(z) \right] \\
& -\left[ \dfrac{f’’’(z)}{2!} (x-z)^2 -\dfrac{f’’(z)}{1!} (x-z) \right] \\
& -\left[ \dfrac{f^{\mathrm{IV}}(z)}{3!} (x-z)^3 -\dfrac{f’’’(z)}{2!} (x-z)^2 \right] -\cdots \\
& -\left[ \dfrac{f^{(n+1)}(z)}{n!} (x-z)^n -\dfrac{f^{(n)}(z)}{(n-1)!} (x-z)^{n-1} \right] ,\end{align}$$

或在化简以后，

$$\varphi’ (z)=-\dfrac{f^{(n+1)} (z)}{n!} (x-z)^n .$$

今取任意函数$\psi (z)$，它在区间$[x_0 ,x]$内是连续的，并且至少在开区间$(x_0 ,x)$内有不等于零的导数$\psi’ (z)$.

对函数$\varphi (z)$及$\psi (z)$应用柯西公式$[114]$：

$$\dfrac{\varphi (x)-\varphi (x_0 )}{\psi (x)-\psi (x_0 )} =\dfrac{\varphi’ (c)}{\psi’ (c)} ,$$

此处

$$x_0 < c < x $$

或

$$c=x_0 +\theta (x-x_0 ) (0 < \theta < 1).$$

因为

$$\varphi (x)=0,\varphi (x_0 )=r_n (x) ,\varphi’ (c)=-\dfrac{f^{(n+1)} (c)}{n!} (x-c)^n ,$$

故

$$r_n (x)= \dfrac{\psi (x)-\psi (x_0 )}{\psi’ (c)} \cdot \dfrac{f^{(n+1)} (c)}{n!} (x-c)^n .$$

今若把函数$\psi (z)$换成满足所设条件的任意函数，我们就可得出余项$r_n (x)$的各种不同的形式.设$\psi (z)=(x-z)^p $，此处$p > 0$.就有：

$$\psi’ (z) =-p(x-z)^{p-1} \quad (x_0 < z < x).$$

显然，这函数满足所设条件.因此

$$r_n (x)=\dfrac{-(x-x_0 )^p}{-p(x-c)^{p-1}} \cdot \dfrac{f^{(n+1)} (c)}{n!} (x-c)^n =\dfrac{f^{(n+1)} (c)}{n!p} (x-c)^{n+1-p} (x-x_0 )^p .$$

因为$c=x_0 +\theta (x-x_0 )$，所以$x-c=x-x_0 -\theta (x-x_0 )=(1-\theta )(x-x_0 )$，因而最后

$$r_n (x)= \dfrac{f^{(n+1)} (x_0 +\theta (x-x_0 ))}{n!p} (1-\theta )^{n+1-p} (x-x_0 )^{n+1} \quad (0 < \theta < 1).$$

这个表达式称为余项的施勒米希-洛希（$\mathrm{O.Schl\ddot{s} milch-Roche}$）式.

由上式给$p$以具体的数值，就可以得出余项的更特殊的形式.令$p=n+1$，就得特别简单的拉格朗日余项：

$$r_n (x)=\dfrac{f^{(n+1)} (c)}{(n+1)!} (x-x_0 )^{n+1} \quad (x_0 \lessgtr c \lessgtr x),$$

它使人想起泰勒公式的紧接着$n$阶导数下面的一项，只是其中的$(n+1)$阶导数不取在$x_0 $处的数值，而是取在某一中值$c$（在$x_0 $与$x$之间）处的数值.

这样，具拉格朗日余项式的泰勒公式就有如下的形式：

$$\left. \begin{align}
f(x) = & f(x_0 )+\dfrac{f’(x_0 )}{1!} (x-x_0 ) +\dfrac{f’’(x_0 )}{2!} (x-x_0 )^2 +\cdots \\
& +\dfrac{f^{(n)}(x_0 )}{n!} (x-x_0 )^n +\dfrac{f^{(n+1)} (c)}{(n+1)!} (x-x_0 )^{n+1} (x_0 \lessgtr c\lessgtr x).
\end{align} \right\rbrace \label{13} \tag{13}$$

若在式内把$f(x_0 )$移至左端，就很易看出，它是有限增量公式$[112]$

$$f(x)-f(x_0 )=f’(c) \cdot (x-x_0 )$$

的直接推广.

虽然由于简单方便大家最乐意应用拉格朗日余项式，但在个别情形，这形式对于估计余项是不适用的，因而不得不改用其他略繁的形式.我们将在这里讲及其中之一，即柯西余项式，它是在施勒米希-洛希的普遍式内令$p=1$而得到的：

$$r_n (x)=\dfrac{f^{(n+1)} (x_0 +\theta (x-x_0 ))}{n!} (1-\theta )^n (x-x_0 )^{n+1} .$$

近似公式

为简单起见，在公式$\eqref{13}$内令$x_0 =0$，而$c$就改写成$\theta x$，此处$0 < \theta < 1\colon $

$$f(x)=f(0)+\dfrac{f’(0)}{1!} x +\dfrac{f’’(0)}{2!} x^2 +\cdots +\dfrac{f^{(n)}(0)}{n!} x^n +\dfrac{f^{(n+1)}(\theta x)}{(n+1)!} x^{n+1} .\label{14} \tag{14}$$

若弃去这里的余项，则得近似公式

$$f(x)\doteq f(0)+\dfrac{f’(0)}{1!} x +\dfrac{f’’(0)}{2!} x^2 +\cdots +\dfrac{f^{(n)}(0)}{n!} x^n ,$$

它用多项式来代替原来性质繁复的函数.但在这一次我们已有可能估计这公式的误差，因为它（依绝对值）刚好等于所弃去的那一项.例如，若$(n+1)$阶导数（至少当变元在$0$与$x$之间变动时）的绝对值是以$M$为界限的，则

$$\vert r_n (x)\vert \leqslant \dfrac{M x^{n+1}}{(n+1)!} .$$

转而讨论初等函数作为例子.我们不再重复$125$的计算，只是把余项写成新的形式.

$1)$令$f(x)=e^x$.近似公式为：

$$e^x \doteq =1+\dfrac{x}{1!} +\dfrac{x^2}{2!} +\cdots +\dfrac{x^n}{n!} ;$$

因为在这里的余项是

$$r_n (x)=\dfrac{e^{\theta x}}{(n+1)!} x^{n+1} ,$$

所以，例如在$x > 0$时，可估计误差如下：

$$\vert r_n (x)\vert < e^x \cdot \dfrac{x^{n+1}}{(n+1)!} .$$

特别情形，若$x=1$，则

$$e\doteq 1+\dfrac{1}{1!} +\dfrac{1}{2!} +\cdots +\dfrac{1}{n!} ,\vert r_n (1)\vert < \dfrac{3}{(n+1)!} .$$

我们在$37$内计算数$e$的近似值时已经应用过与此类似的公式，但余项的估计系由另一方法得出，那里的结果比较精确些.

$2)$取$f(x)=\sin{x}$，则得

$$\sin{x} \doteq x-\dfrac{x^3}{3!} +\dfrac{x^5}{5!} -\cdots +(-1)^{m-1} \dfrac{x^{2m-1}}{(2m-1)!} .$$

在这情形余项为：

$$r_{2m } (x) =\dfrac{\sin{\left( \theta x+(2m+1)\dfrac{\pi }{2} \right) }}{(2m+1)!} x^{2m+1} =(-1)^m \cos{\theta x} \cdot \dfrac{x^{2m+1}}{(2m+1)!} ,$$

并且误差很容易估计为：

$$\vert r_{2m} (x)\vert \leqslant \dfrac{\vert x\vert ^{2m+1}}{(2m+1)!} .$$

特别情形，若我们只取一项而令

$$\sin{x} \doteq x,$$

则为着要使误差小于$0.001$，就只要取（算作$x > 0$）

$$\dfrac{x^3}{6} < 0.001,$$

或

$$x < 0.1817,$$

这大约等于$10^{\circ }$.在应用二项的近似公式

$$\sin{x} \doteq x-\dfrac{x^3}{6} $$

时，要达到同一的准确度，就只要取

$$\dfrac{x^5}{120} < 0.001,$$

或

$$x < 0.6544(\doteq 37.5^{\circ});$$

若限制角$x < 0.4129(\doteq 23.5^{\circ})$，则误差甚至可$< 0.0001$，余类推.

我们看到，泰勒多项式的项数愈多时，它就以愈大的准确度及在更长的距离内表达原来的函数.

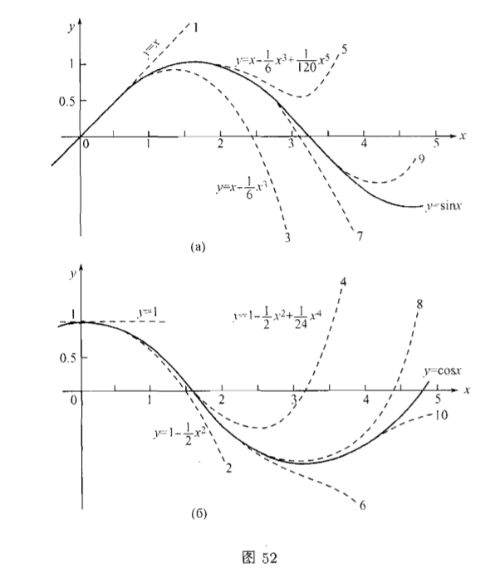
图$52,a$明显地b表明这些事实，在图中与函数$y=\sin{x}$的图像并列的是各多项式的图像，这些多项式是：

$$y=x,y=x-\dfrac{x^3}{6} ,y=x-\dfrac{x^3}{6} +\dfrac{x^5}{120} ,$$

等等.

$3)$类似地，对于$f(x)=\cos{x}$就有

$$\cos{x} \doteq 1-\dfrac{x^2}{2!} +\dfrac{x^4}{4!} -\cdots +(-1)^{m} \dfrac{x^{2m}}{(2m)!} ,$$

并且

$$r_{2m +1} (x) =(-1)^{m+1} \cos{\theta x} \cdot \dfrac{x^{2m+2}}{(2m+2)!} ,$$

因此

$$\vert r_{2m+1} (x)\vert \leqslant \dfrac{\vert x\vert ^{2m+2}}{(2m+2)!} ,$$

例如，对于公式

$$\cos{x} \doteq 1-\dfrac{x^2}{2!} $$

误差

$$\vert r_3 (x)\vert \leqslant \dfrac{x^4}{24} ,$$

就说是，在$x < 0.2213(\doteq 13^{\circ})$时误差$< 0.0001$，余类推.在图$52,б$中有着函数$y=\cos{x}$的图像及下面诸多项式

$$y=1,y=1-\dfrac{x^2}{2} ,y=1-\dfrac{x^2}{2} +\dfrac{x^4}{24} $$

等等的图像以便比较.

请读者注意，这与$62,63,107$诸目的公式比较起来已有很重大的进步：现在我们已能确定误差的界限，并且能够得到具任何准确度的展开式.

还将指出，泰勒公式是构成完全另一种类型的近似公式的来源.

$4)$作为例题，讨论与半径相较是很微小的圆弧被近似地引直时的惠更斯（Ch.Huygens）公式.

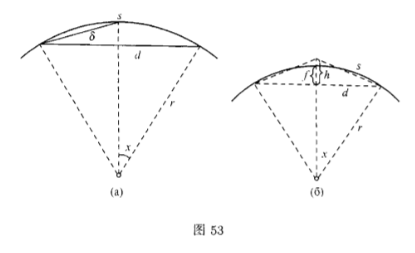
设$s$是弧长，$d$是对应于它的弦，而$\delta $是对应于半弧的弦（图$53$）.问题是要尽可能准确地用近似公式

$$s\doteq Ad+B\delta $$

来表示弧长$s$，此处$A,B$是待定系数.

若$r$是圆的半径，而$2x$是对应于弧$s$的圆心角，则有

$$d=2r\cdot \sin{x} =2r\left( x-\dfrac16 x^3 +\dfrac{\theta’}{120} x^5 \right) \quad (0 < \theta’ < 1).$$

类似地，把$x$换成$\dfrac{x}{2}$，就又有

$$\delta =2r\cdot \sin{\dfrac{x}{2}} =2r \left( \dfrac12 x-\dfrac{1}{48} x^3 +\dfrac{\theta’’}{3840} x^5 \right) \quad (0 < \theta’’ < 1).$$

由此

$$Ad+B\delta =2r\left[ \left( A+\dfrac12 B\right) \cdot x-\left( \dfrac16 A+\dfrac{1}{48} B\right) \cdot x^3+\left( \dfrac{\theta’}{120} A+\dfrac{\theta’’}{3840} B\right) \cdot x^5 \right] ,$$

可是$s=2rx$，自然必须选取$A$及$B$使

$$A+\dfrac12 B =1,\dfrac16 A+\dfrac{1}{48} B=0,$$

因为这样一来，在所考察的公式中，左端与在右端的差将仅只有含有$x^5$的项了.由上二式解得$A$及$B$的数值为$A=-\dfrac13 ,B=\dfrac83$，而公式成为

$$s=\dfrac{8\delta -d}{3} =2\delta +\dfrac{2\delta -d}{3} .$$

很易看出，其误差$\Delta $可估计为：

$$\vert \Delta \vert < r\cdot \dfrac{x^5}{180} .$$

例如，在圆心角为$30^{\circ}$时，即$x=\dfrac{\pi}{12}$时，根据这一估计，就有$\vert \Delta \vert < r\cdot 0.000\;007$；实际上$s=r\cdot 0.532\;599\cdots $，而依惠更斯公式得$s=r\cdot 0.532\;593\cdots $，所以误差并未超出规定的限度.

$5)$为着同一目的，切比雪夫（Chebyshev）曾给出下面的法则：弧长近似地等于作在弦上而高为矢的$\sqrt{\dfrac43}$倍的等腰三角形两腰之和（图$53,б$）.

暂设$h=\gamma f$；下面就要说明：若设$\gamma =\sqrt{\dfrac43 }$，则确能得（某种意义上的）最佳近似.

以上我们知道

$$\dfrac12 d=r\cdot \sin{x} =r\left( x-\dfrac16 x^3 +\dfrac{\theta_1 }{120} x^5 \right) (0 < \theta_1 < 1);$$

相仿地，

$$h=\gamma f=\gamma r(1-\cos{x} )=\gamma r(\dfrac12 x^2 -\dfrac{\theta_2 }{24} x^4) (0 < \theta_2 < 1).$$

用$s^{\ast }$记上述切比雪夫法则中等腰三角形的两腰之和，即有

$$\begin{align}
s^{\ast} & =2\sqrt{\left( \dfrac12 d\right)^2 +h^2} =2rx\sqrt{\left( 1-\dfrac16 x^2+\dfrac{\theta_1 }{120} x^4 \right)^2 +\gamma^2 \left( \dfrac{x}{2} -\dfrac{\theta_2 }{24} x^3\right)^2} \\
& =2rx \sqrt{1+\left( \dfrac{\gamma^2 }{4} -\dfrac13 \right) x^2 +ax^4 +bx^6 +cx^8} .\end{align}$$

现在，为使根式中消去$x^2$项，设它的系数等于$0$，于是便得$\gamma =\sqrt{\dfrac43 }$.

为估计误差，把$s^{\ast}$式改写成

$$s^{\ast} =2rx\sqrt{1+Ax^4} ,\label{15} \tag{15}$$

而$A$的表达式中则含有$x$的二次项与四次项.设$x < \dfrac{\pi}{2}$，则有$x^2 < 2.5$，$x^4 < 6.5$，而$A$的估计式为$\vert A\vert < 0.006$，因而$\vert A\vert x^4 < 0.4$.

为简便起见，把$Ax^4$设为$y$，依有限增量公式$[112]$有

$$\sqrt{1+Ax^4} =\sqrt{1+y} =1+\dfrac{y}{2\sqrt{1+\theta y}} \quad (0 < \theta < 1).$$

最后的分式可估计如下：

$$\left\vert \dfrac{y}{2\sqrt{1+\theta y}} \right\vert < \dfrac{\vert y\vert }{2\sqrt{1-\vert y\vert }} =\dfrac{\vert A\vert x^4}{2\sqrt{1-\vert A\vert x^4}} < \dfrac{0.06x^4}{2\sqrt{0.6}} < \dfrac12 0.1x^4 .$$

把表达$s^{\ast}$的$\eqref{15}$式与刚才所得结果比较一下，则见

$$s^{\ast} =s+\rho ,$$

其中$\vert \rho \vert < 0.1rx^5.$

误差的阶跟惠更斯公式的一样.

在第二卷十一章讲无穷级数的时候，我们还要再讨论带余项的泰勒公式；在那里这公式将有很大的作用.