关系与括号

本书的语言，像大多数数学教科书那样，是由普通的语言及一串用以叙述理论的专用符号构成.除了这些按照需要而引入的专用符号之外，我们还要利用通用的数学逻辑符号$\neg $，$\land $，$\lor $，$\Longrightarrow $，$\Longleftrightarrow $，它们分别表示否定词“非”，系词“与”，“或”，“蕴含”，“等价”.

在逻辑学中常使用符合$\And $，而不用$\land $.蕴含符号$\Longrightarrow $常写成$\to $，而等价关系写做$\leftarrow \to $或$\leftrightarrow $.但是为了不更换分析中传统的极限记号$\to $，在本教程中仍使用上面给出的记号.

作为例子，我们举出代表三种不同旨趣的意见：

$L$.“如果采用适合于发现的记号，$\cdots \cdots $那么，思考工作就能得到惊人的简化.”（莱布尼茨）

莱布尼茨$(\mathrm{Leibniz} )(1646-1716)$是杰出的德国学者、哲学家和数学家.他与牛顿一起享有发现无穷小分析基础的荣誉.

$P$.“数学是把不同实体统一命名的艺术.”（庞加莱）

庞加莱$(\mathrm{Poincar \acute{e} } )(1857-1912)$是法国数学家，他的卓越思想革新了数学的许多部门并在数学物理中得到具有重大价值的应用.

$G$.“自然界这部巨著是用数学语言写成的.”（伽利略）

伽利略$(\mathrm{Galileo} )(1564-1642)$是意大利学者，伟大的自然科学家.他的工作成为后来关于空间和时间的全部物理概念的基础.他是现代物理学之父.

于是，根据上述记号，有下页开头表的写法.

$$\begin{array}{c|c} \hline 写法 & 表示 \\ L\Rightarrow P & L蕴含P \\ L\Leftrightarrow P & L与P等价 \\ ((L\Rightarrow P)\land (\neg P)) \Rightarrow (\neg L) & 若P由L推出，而P不真，则L不真. \\ \neg ((L\Leftrightarrow G)\lor (P\Leftrightarrow G)) & G既不等价于L，也不等价于P \\ \hline \end{array}$$

我们将会看到，只使用形式化记号，回避普通语言，并非总是明智的.

另外，我们发现，由较简单的命题构成复杂命题时，使用了括号，正像写代数式那样，它们起着有关结构层次的作用.同代数中一样，为了节省括号，可以约定“运算次序”.为此目的，我们对符号规定如下的优先次序：

$$\neg ,\land ,\lor ,\Rightarrow ,\Leftrightarrow .$$

在这样约定下，式子$\neg A\land B\lor C\Rightarrow D$应解释成$(((\neg A)\land B)\lor C)\Rightarrow D$，而$A\lor B\Rightarrow C$应解释成$(A\lor B)\Rightarrow C$，而不是$A\lor (B\Rightarrow C)$.

对于表示$A$蕴含$B$或$B$由$A$推出的写法$A\Rightarrow B$，我们常常赋予它另一种文字解释：$B$是$A$的必要特征或必要条件，同样地，$A$是$B$是充分特征或充分条件.于是关系$A\Leftrightarrow B$可用下面任一种方法去解释：

对于$B$，$A$既是必要的又是充分的；

$A$成立，当且仅当$B$成立；

当且仅当$B$成立，有$A$成立；

$A$与$B$等价.

因此，写法$A\Leftrightarrow B$表示$A$蕴含$B$，同时$B$蕴含$A$.

对式子$A\land B$中连接词“与”的用法不需作解释了.

然而应注意，在式子$A\lor B$中的连接词“或”，不是区分连接词，也就是说只要命题$A$，$B$中有一个为真，$A\lor B$就正确.例如，设$x$是$x^2-3x+2=0$的实数.这时可以说下列关系成立：

$$(x^2-3x+2=0)\Leftrightarrow (x=1)\lor (x=2).$$

关于证明的注记

典型的数学论断具有$A\Rightarrow B$这种形式，这里$A$是前提.$B$是结论.证明这个论断，就是要建立一串蕴含关系

$$A\Rightarrow C_1 \Rightarrow \cdots \Rightarrow C_n \Rightarrow B,$$

其中每个蕴含关系或为公理，或为已证明了的断语.

$A\Rightarrow B\Rightarrow C$是$(A\Rightarrow B)\land (B\Rightarrow C)$的缩写.

在证明中，我们将使用古典的推证法则：若$A$真且$A\Rightarrow B$，那么$B$也真.

在用反证法证明时，我们还将使用排中律，根据它，不论命题$A$的内容是什么，$A\lor \neg A$（$A$或非$A$）总是正确的.因此，我们同时还采用$\neg (\neg A)\Leftrightarrow A$，即一个命题两次否定等价于原命题.

某些专门记号

为方便读者及简化文字叙述，约定分别用记号$\blacktriangleleft $及$\blacktriangleright $来表示证明的开始和结束.

还约定，当方便时，用专门的记号$\colon = $（据定义等于）引进定义，其中两点放在被定义的对象一边.

例如，式子

$$\int_a^b f(x)\mathrm{d} x\colon =\lim_{\lambda (P)\to 0} \sigma (f,P,\xi )$$

是用右端定义左端.而右端的含义认为是已知的.

类似地，对已有定义的式子，也用这个记号引进简缩记法.例如，式子

$$\sum_{i=1}^n f(\xi_i )\Delta x_i =\colon \sigma (f,P,\xi )$$

就是引进记号$\sigma (f,P,\xi )$表示左端的专门和式.

最后的注记

注意，在这里我们实际上只谈到了记法，并没有分析逻辑推导形式，也没涉及诸如真实性、可证明性、可推导性等构成数理逻辑研究对象的深刻问题.

如果我们形式逻辑，怎么建立数学分析呢？这里使人们得到一些安慰的是，我们知道的，或说得更恰当些，我们会的，总比做形式时所需要的多些.这可以用一句格言来说明：当你要求一只蜈蚣解释它是怎样控制那么多条腿的时候，它早已学会走路了.

整个科学的经验使我们断定，昨天认为明显、简单且不能分的东西，今天可能受到重新审查或把它精确化.数学分析的许多概念就曾经是这样的（无疑，未来也是这样）.它的最重要的一些定理和工具早在$17$、$18$世纪就已经发现，然而，只是在创立了极限理论，以及这个理论所必需的、逻辑上完全合格的实数理论（在$19$世纪）之后，数学分析才获得了现代形式化的、含义确切的、从而为人们理解的形式.

在第二章中，我们正是从实数理论的这种水平上开始建造数学分析的整个大厦.

如序言所说，希望尽快了解微积分学本身的基本概念和有效方法的读者，可立刻从第三章开始学，只是在有必要时，再回到头两章查阅相应的地方.

练习

用$1$表示命题正确，用$0$表示命题不正确.这时，对命题$\neg A$，$A\land B$，$A\lor B$，$A\Rightarrow B$中的每一个，可建立一个所谓真假表，它依据命题$A,B$的真实性，指出这个命题的真实性.这些表是逻辑运算$\neg ,\land ,\lor ,\Rightarrow $的形式定义.见下页所画的四个表.

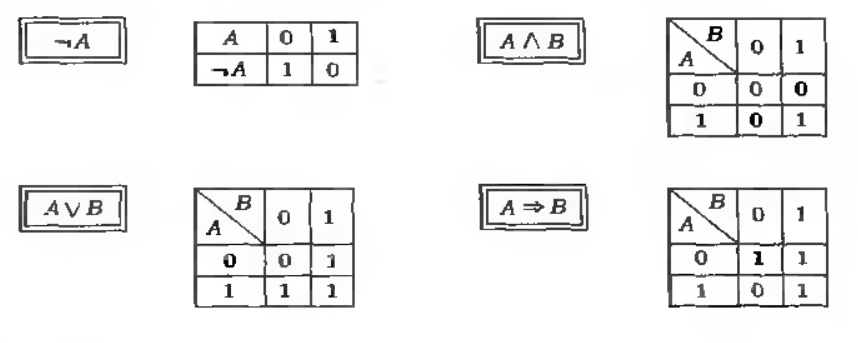
$1$.验证这些表中所指示的一切是否都与你关于相应的逻辑运算的通常观念相符号（要特别注意若$A$不真，则$A\Rightarrow B$总是真的.）

解$\quad $对关于相应的逻辑运算的通常观念汇总列表如下：

$$\begin{array}{cc|c|c|c|c} \hline A & B & \neg A & A\land B & A\lor B & A\Rightarrow B \\ \hline 0 & 0 & 1 & 0 & 0 & 1 \\ 0 & 1 & 1 & 0 & 1 & 1 \\ 1 & 0 & 0 & 0 & 1 & 0 \\ 1 & 1 & 0 & 1 & 1 & 1 \\ \hline \end{array}$$

经比较，关于相应的逻辑运算的通常观念与上述所画的四个表中所指示的一切都相符合.

$2$.试证下面的简单关系成立，它们在数学的论证中极为重要且有广泛的应用.

$(a)\neg (A\land B)\Leftrightarrow \neg A\lor \neg B$；

$(b)\neg (A\lor B)\Leftrightarrow \neg A\land \neg B$；

$(c)(A\Rightarrow B)\Leftrightarrow (\neg B\Rightarrow \neg A)$；

$(d)(A\Rightarrow B)\Leftrightarrow \neg A\lor B$，

$(e)\neg (A\Rightarrow B)\Leftrightarrow A\land \neg B$.

解$\quad (a)$用真值表法判断$\neg (A\land B)\leftrightarrow \neg A\lor \neg B$是否为重言式.此等价式的真值表如下所示，从表可知它是重言式，因而$\neg (A\land B)$与$\neg A\lor \neg B$等值，即$\neg (A\land B)\Leftrightarrow \neg A\lor \neg B$.

$$\begin{array}{cc|c|c|c|c|c|c} \hline A & B & \neg A & \neg B & A\land B & \neg (A\land B) & \neg A\lor \neg B & \neg (A\land B)\leftrightarrow \neg A\lor \neg B \\ \hline 0 & 0 & 1 & 1 & 0 & 1 & 1 & 1 \\ 0 & 1 & 1 & 0 & 0 & 1 & 1 & 1 \\ 1 & 0 & 0 & 1 & 0 & 1 & 1 & 1\\ 1 & 1 & 0 & 0 & 1 & 0 & 0 & 1 \\ \hline \end{array}$$

$(b)$用真值表法判断$\neg (A\lor B)\leftrightarrow \neg A\land \neg B$是否为重言式.此等价式的真值表如下所示，从表可知它是重言式，因而$\neg (A\lor B)$与$\neg A\land \neg B$等值，即$\neg (A\lor B)\Leftrightarrow \neg A\land \neg B$.

$$\begin{array}{cc|c|c|c|c|c|c} \hline A & B & \neg A & \neg B & A\lor B & \neg (A\lor B) & \neg A\land \neg B & \neg (A\lor B)\leftrightarrow \neg A\land \neg B \\ \hline 0 & 0 & 1 & 1 & 0 & 1 & 1 & 1 \\ 0 & 1 & 1 & 0 & 1 & 0 & 0 & 1 \\ 1 & 0 & 0 & 1 & 1 & 0 & 0 & 1\\ 1 & 1 & 0 & 0 & 1 & 0 & 0 & 1 \\ \hline \end{array}$$

$(c)$用真值表法判断$(A\Rightarrow B)\leftrightarrow (\neg B\Rightarrow \neg A)$是否为重言式.此等价式的真值表如下所示，从表可知它是重言式，因而$(A\Rightarrow B)$与$(\neg B\Rightarrow \neg A)$等值，即$(A\Rightarrow B)\Leftrightarrow (\neg B\Rightarrow \neg A)$.

$$\begin{array}{cc|c|c|c|c|c} \hline A & B & \neg B & \neg A & A\Rightarrow B & \neg B\Rightarrow \neg A & (A\Rightarrow B)\leftrightarrow (\neg B\Rightarrow \neg A) \\ \hline 0 & 0 & 1 & 1 & 1 & 1 & 1 \\ 0 & 1 & 0 & 1 & 1 & 1 & 1 \\ 1 & 0 & 1 & 0 & 0 & 0 & 1\\ 1 & 1 & 0 & 0 & 1 & 1 & 1 \\ \hline \end{array}$$

$(d)$用真值表法判断$(A\Rightarrow B)\leftrightarrow \neg A\lor B$是否为重言式.此等价式的真值表如下所示，从表可知它是重言式，因而$(A\Rightarrow B)$与$\neg A\lor B$等值，即$(A\Rightarrow B)\Leftrightarrow \neg A\lor B$.

$$\begin{array}{cc|c|c|c|c} \hline A & B & \neg A & A\Rightarrow B & \neg A\lor B & (A\Rightarrow B)\leftrightarrow \neg A\lor B \\ \hline 0 & 0 & 1 & 1 & 1 & 1 \\ 0 & 1 & 1 & 1 & 1 & 1 \\ 1 & 0 & 0 & 0 & 0 & 1 \\ 1 & 1 & 0 & 1 & 1 & 1 \\ \hline \end{array}$$

$(e)$用真值表法判断$\neg (A\Rightarrow B)\leftrightarrow A\land \neg B$是否为重言式.此等价式的真值表如下所示，从表可知它是重言式，因而$\neg (A\Rightarrow B)$与$A\land \neg B$等值，即$\neg (A\Rightarrow B)\Leftrightarrow A\land \neg B$.

$$\begin{array}{cc|c|c|c|c|c} \hline A & B & \neg B & A\Rightarrow B & \neg (A\Rightarrow B) & A\land \neg B & \neg (A\Rightarrow B)\leftrightarrow A\land \neg B \\ \hline 0 & 0 & 1 & 1 & 0 & 0 & 1 \\ 0 & 1 & 0 & 1 & 0 & 0 & 1 \\ 1 & 0 & 1 & 0 & 1 & 1 & 1 \\ 1 & 1 & 0 & 1 & 0 & 0 & 1 \\ \hline \end{array}$$