《数学史》第二章 希腊数学的起源
这些从古代文化中发展起来的技术,和它们所累积的巨大知识宝库,将永远引起人们的赞叹和惊奇.但是我们找不出什么证据来证明,他们是沿着科学化的道路发展的.它们所获得的法则,大都是经验性的,充其量也不过是少数简单事例的推广.知识就是力量,只是由于需要的驱使,人们才去追求知识.巴比伦的天文学尤其如此,它是从来也离不开神话和魔术的.为了知识本身而去追求知识的概念,对于巴比伦人和埃及人来说,是完全不适合的,这要一直等到希腊人来进行.科学真正的起源不是在巴比伦,也不是在埃及,而是在爱琴海的爱奥尼亚海岸一个小小的希腊殖民地.尽管如此,古代文化对希腊的影响很大,希腊人从古代文化中继承了原始资料.“希腊科学的奇迹”是由巴比伦人和埃及人预先准备好了的.
希腊人在数学方面比在任何其他学科有着更惊人的进步.他们不仅在数学的各个部分中作出了显著的、不朽的贡献,而且还为它们以后的发展奠定了永久的基础.我们转向希腊人,乃是为了寻找严格演绎证明的概念,亦即寻找在定义、公理和公设的基础上通过一系列定理来发展一门学科,以及不断争取全面推广和抽象的方法.
在希腊数学史中有三个时期:
$1$.毕达哥拉斯学派时期.
$2$.柏拉图和柏拉图学园时期.
$3$.亚历山大学派时期.
但是在此以前,大约在公元前$6$世纪,在爱琴海沿岸已经略见端倪.这些新学问的先驱者是米利都的泰勒斯、阿那克西米尼和阿那克萨哥拉.泰勒斯曾周游各地,在他访问埃及期间,学到了在那里已经实施着的土地测量的经验法则.
大约在公元前$330$年,亚里士多德的弟子欧德摩斯精心编纂了一本从最初起始的希腊几何学史,这就是人们常常提到的《欧德摩斯摘要》.公元$5$世纪,普罗克洛斯曾简短地评论过至欧几里得为止的早期几何学史,
$\mathrm{Proclus} ,Procli\;in\;Primum\;Euclidis\;Elementorum\;Librum\;Commentarii,\mathrm{Leipzig} ,1873.\mathrm{Ed.Friedlein} .$
人们以为这是以欧德摩斯为根据的.在提到爱奥尼亚学派时,普罗克洛斯曾宣称:“泰勒斯是去到埃及并把几何学这一专门知识带回希腊的第一个人.他本人发现了许多命题,并将许多其他基本原理告诉他的继承者,在某些方面他的方法更普遍,在另一些方面又更经验性些.”普罗克洛斯把下列五个命题的发现归功于泰勒斯:
$1$.任何圆周都要被其直径平分.
$2$.等腰三角形的两底角相等.
$3$.两直线相交时,对顶角相等.
$4$.若已知三角形的一边和两邻角,则此三角形完全确定.
$5$.半圆周角是直角.
尽管泰勒斯在数学的实用方面表现出的兴趣不大,但据说他曾用手杖的投影与金字塔的投影作比较的方法计算出金字塔的高度.果真如此,那就意味着泰勒斯已经熟悉相似三角形的基本性质了.关于三角形三内角之和的知识也要归功于他,但其证据远不是无可争论的.可以肯定的是,泰勒斯把几何学作为一门演绎科学确立了起来.上述一切事实对埃及人来说都是早已知道了的,只是埃及人一直没有把它们记载下来.而在泰勒斯那里,它们却成了几何科学的开端.
泰勒斯也熟悉巴比伦人的天文学,据说他曾利用巴比伦人的记载预测过一次日食,这次日食在公元前$585$年实际发生了.很难理解这是怎么发生的.首先,日食的真正本质对他来说想必是不了解的,因为他认为地球乃是浮在水面上的一块圆盘.其次,很难使人相信,早在公元前$6$世纪的时候,巴比伦人的记载就已经广泛到可以作出如此准确预测的程度.
爱奥尼亚学派历经的时间不久,到了公元前$6$世纪末,由于波斯游牧民族的进攻,人们都向西方逃难,这就把希腊文化带到了西方.意大利和西西里岛变成了学术的新中心,学术在意大利领土上有了惊人的发展,尤其是在数学方面.早在公元前$6$世纪,毕达哥拉斯(公元前$580-$前$497$)就已经在意大利南部克罗顿建立了学派.它原来只是一个宗教团体,但是它的成员都积极追求学问.毕达哥拉斯学派没有给后人留下什么著作,但可以很明显地看出,这个学派的数学修养非常高.普罗克洛斯记载说:“毕达哥拉斯学派把数学研究变成了一种自由教育的形式,从头来检查它的原理.”在他们手里,整个数学变得更抽象,更加脱离经济生活的需要了.在这个学派的数学发现中,其奠基人本身的贡献大小就永远只能由后人去猜测了.
毕达哥拉斯学派对于自然现象中的某些数学关系,已经有了印象.他们已经知道,长度与$4,3,2$成比例的振动弦能够产生一个主音以及它的第五音和第八音.由此导致一个信念:终极的实在可以在数字里找到.亚里士多德说:“毕达哥拉斯学派似乎把数看成本质,这就是说,看成是万物的本原.”结果,关于数的科学吸引了他们强烈的注意,而前人所发展起来的计算技术(实用算术)却不大为他们所关心了.他们首先把抽象的数的概念放到首要地位.他们把数分成了奇数和偶数、素数和合数、完全数等.他们在研究这些数的时候,发现了许多相当复杂的定理,其中有许多后来被欧几里得收集到他的著作《几何原本》中.
毕达哥拉斯学派的算术与几何学有着密切联系.它的根据是堆成各种形状的一堆堆的鹅卵石或石头,这样他们就用图形来表达数——三角形数、正方形数等.起始$n$个自然数的和,即$\dfrac{1}{2} n(n+1)$,形成一个三角形数;起始$n$个奇数的和,即$1+3+5+\cdots +(2n-1)$,形成一个正方形数,等等.但是人们发觉,这和毕达哥拉斯学派的另一发现有着严重的抵触,那就是正方形的对角线与其一边之比不能表示为两个正数之比,因此无法再主张所有的量都有一个共同度量.某些线和其他线不能通约的问题,不仅对毕达哥拉斯学派形成了一个严重的障碍,而且后来的事实证明,它在整个希腊几何学史中也是一块绊脚石.由于人们试图寻找一种不使算术完全脱离几何学的解决办法,这就导致一种新型数的引进,那就是无理数.
对于毕达哥拉斯学派来说,研究几何学也和研究算术一样,都是为研究而研究的.有很多定理应该归功于他们.除了关于直角三角形的著名定理之外,毕达哥拉斯学派还熟悉平行线的性质,他们利用这些性质证明了三角形的三内角之和等于两直角,由此他们推证了关于多边形诸内角之和的定理.欧几里得的《几何原本》中大多数是关于直线与面积之间关系的定理,这都是他们已经知道了的.他们还发展了关于比例的理论,并且熟悉欧几里得《几何原本》第六卷中的论题.由于某些原因,他们对于圆的几何学并无多大兴趣.他们对数学发展的主要贡献就是他们给数学以演绎的特性.对他们来说,几何学已经不再仅仅是一些靠经验发现的规则的汇集了.
毕达哥拉斯学派的影响越来越大,在它的奠基人于公元前$497$年逝世之后,这个学派在塔伦图姆地区还一直繁盛到近$4$世纪末.以菲洛劳斯和阿契塔为代表的后期毕达哥拉斯学派,仍然保持着其奠基人的传统,他们的工作对数学发展所产生的巨大影响,历时达两个世纪之久.
哲人派
在公元前$480$年的萨拉米斯战役中击败了薛西斯率领的波斯大军之后,雅典很快地兴起,成了世界的商业中心和文化中心.伯里克利花了很多钱来装饰他的首都.因为当时奴隶占国家人口的大多数,劳动力并不缺乏,这就在有闲阶级中产生了一种强烈的欲望,要求有某种形式的文化,作为社会的或政治的帮助.一批职业教师满足了这个要求,这些教师感到执教是光荣的,并且以此为生.这些人被大家称为哲人,或智者.他们和毕达哥拉斯学派不同,并没有形成一个以某种共同学说或哲学为特征的阶级或派别.他们的兴趣主要集中在传授辩论的艺术,但由于他们对“国民”教育产生了广泛兴趣,这就使他们做了一些有益的事.虽然数学并不是他们的主要业务,但是他们在数学历史中的重要性并不小.他们当中许多人作出了有价值的贡献,特别是在关于圆的几何性质方面(这里要提醒一下,它一直是毕达哥拉斯学派所忽视的).这主要是由于他们在研究古代三个古典问题上的兴趣.
关于这三个问题,数学家们曾经仔细思索了许多世代.它们是:
$1$.三等分一个角,或者同样的说法是,三等分一段圆弧.
$2$.使一立方体体积加倍,亦即求出一立方体的边,使些立方体的体积是给定立方体体积的二倍.
$3$.化圆为方,亦即求出一个正方形或其他直线图形,使其面积与给定圆形的面积恰好相等.
二等分一个角的问题即使对古代的几何学家来说,也不会引起任何困难.然后一个角的三等分曾被证明是不可能的.现在已经知道这个问题仅靠直尺和圆规作有限次操作是不可能解决的,而直尺和圆规当然是希腊人所能采用的仅有的工具.伊利斯的哲人派中有一个著名的人物,叫做希庇亚斯.他是一个以一切学问为已任的人,对这个问题曾经钻研过,并且认识到只使用直尺和圆规是不够的,还要求助于其他工具,其中包括非圆弧形曲线的使用.希庇亚斯所使用的一种叫做割圆曲线,这个名称的由来是因为它也可以解决求面积问题,就像它可以解决一个角的三等分(其实可以任意等分)问题一样.
普罗克洛斯曾用这样几句话来描述这种曲线:“在正方形$ABCD$中,以$A$为中心,$AB$为半径画出$\dfrac{1}{4} $个圆$BED$.使直线$AB$均匀地绕其端点$A$移动,以使另一端点$B$在给定时间内沿着整个$BED$弧移动.同时使直线$BC$也均匀地移动,并且总是保持与直线$AD$平行.直线与移动半径的交点轨迹就是曲线$BFG$.这条曲线就是割圆曲线.”(图$1$)
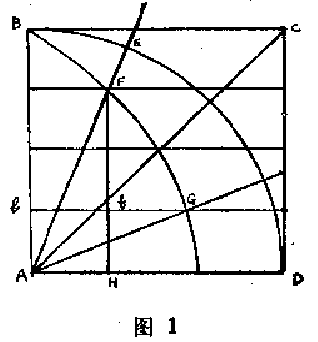
它的性质是:若向圆周任意作一直线$AFE$,则圆的$\dfrac{1}{4} $弧$BED$与弧$ED$之比等于直线$BA$与$FH$之比.
$\angle BAD\colon \angle EAD=\stackrel \frown{BED} \colon \stackrel \frown{ED} =BA\colon FH$.要三等分$\angle EAD$,可在$f$处把$FH$分成两部分,使得$2Hf=fF$.过$f$作$bfG$与$AD$平行,$bfG$在$G$点与曲线相交,连接$AG$.于是$\angle GAD$便是$\angle EAD$的$\dfrac{1}{3} $.
由于一条直线能够以任意比例分成任意多部分,所以圆的$\dfrac{1}{4}$也能如此,因而一个角可以三等分或任意等分.因为$FH\colon AB$等于$\angle FAD \colon \dfrac{\pi }{2} $,所以割圆曲线画出后一定能帮助我们达到求圆面积的目的.
倍立方问题的产生,很可能是根源于人们企图把毕达哥拉斯定理推广.要作一个正方形,使其面积等于给定正方形面积的两倍,这是一件简单的事.这也许就使人联想到求一个立方体的边,使其体积等于给定立方体体积的两倍的问题.但是根据埃拉托色尼所述,公元前$430$年雅典城发生过鼠疫,居民们曾向阿波罗神殿请求驱除疫疠.他们受命要把祭坛加大一倍,而不准有损于它的立方体形状.因此倍立方问题往往被称为阿波罗问题.和上述三等分角的问题一样,它也是不能单用直尺和圆规来解决的.但在希俄斯有一位天才数学家希波克拉底(公元前$430$年前后享有盛名)曾研究过相似三角形和比例理论,指出这个问题可以归结为求两线段之间两个比例中项的问题,这两条线段中有一条的长度是另一条的两倍.假定以$a$和$2a$表示这两线段,$x$和$y$代表两个比例中项,则有$a\colon x=x\colon y=y\colon 2a$,或$ay=x^2 $,$y^2 =2ax$,从而$y^3=2x^3 $.后来人们对这个问题的解决方法,就都是尝试求两条线段之间的两个比例中项了.
但是希波克拉底最容易使人记起的一件事,就是他证明了半月形面积可以化为三角形面积,这是把曲线形面积化为直线形面积的第一个例子.他还熟悉这样一个事实:圆面积与其直径的平方成正比.由此他从一个等腰直角三角形$ABC$(图$2$)出发,在三条边上各作一个半圆.
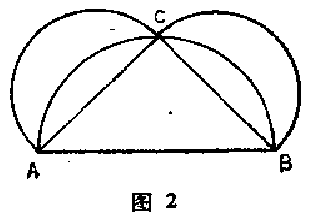
根据毕达哥拉斯定理,$AB$上那个半圆的面积等于$AC$和$CB$上两上半圆的面积之和.如果现在从整个图中移去$AB$上的半圆,则留下的是两个相等的半月形.但如果从同一图中移去两个相等边上的半圆,则只剩下三角形$ABC$.所以三角形$ABC$的面积一定等于两个半月形的面积.正是由于希波克拉底证明了曲线形的面积能化为直线形的面积,才激起了他对求积问题的兴趣.
在哲人派中,安提丰和布里松也研究过求圆的面积问题.前者从一正方形出发,在一圆内作内接正方形.用不断平分弧段的办法使多边形的边不断增加,多边形的面积便逐渐接近圆的面积.安提丰相信,如果不断增加边的数目,最后一定能“耗尽”多边形和圆之间的面积,从而达到圆面积成方(求积)的目的.与他同时代的布里松把这个问题更推进了一步,既考虑了圆内接多边形,也考虑了圆外切多边形,但是没有什么证据说明,他相信真正的面积乃是两者的算术平均值.这种方法导致完全严格却很麻烦的穷竭法,两个世纪以后阿基米德曾十分有效地使用了它.
然而,安提丰和布里松的结论使希腊人为之皱眉.希腊人认为,多边形绝不可能与一个圆完全相合,因为直线永远不能恰好落在曲线上.承认这点就意味着承认量可以无限分割,而那却是希腊人所不能接受的观点.埃利亚人芝诺使这些争论达到尖锐的地步.芝诺想到了一系列巧妙的悖论,借以批驳一条线的无限可分割性,并由此论证了运动之不可能.
这些悖论中首先是关于二分法的.运动是不可能的.飞矢在达到终点之前,必须先到达它路程的中点,但在到达中点前,必须先到达四分之一处,如此类推以至无穷.因此运动甚至不可能有开始的时候.
其次是阿基里斯和龟.飞毛腿阿基里斯比龟跑得快$10$倍,龟先开步$100$码,阿基里斯却永远赶不上它.因为当阿基里斯到达龟的起点时,他还落后$10$码,而当他再跑$10$码时,还要落后$1$码,如此类推.因此他总要落后于龟.可是经验却告诉我们,他会很快赶上龟的.
这些悖论和其他类似的悖论,使当时的数学家感到很困惑,后来也一直如此.为了避免这种二难推论,希腊人在他们的几何学中抛弃了所有关于无限小和无限大的观念.芝诺并不是数学家,但是他的批评意见却对希腊几何学方法日趋严谨起了作用,而他的悖论解决,对以后的几何学进展一直有着深远的影响.
柏拉图及其学园
雅典的商业优势持续了半个多世纪.波斯游牧民族侵扰的危险消除以后,统一就让位于不和与猜忌了.雅典与斯巴达之间的相互猜忌引起了伯罗奔尼撒战争,这场战争除了短暂的间歇之外,一直延续到公元前$404$年,那一年雅典人被迫投降.雅典人的影响虽然衰落了,但是他们的智力却仍旧完好无损.这时期就是苏格拉底(公元前$469-$前$399$)和他的青出于蓝的弟子柏拉图(公元前$428-$前$348$)的时期.苏格拉底的主要兴趣是国家,以及如何更好地为国家服务,数学对他的吸引力极小.与此相反,柏拉图对伦理学和政治性的问题兴趣不大.他游历很广,访问过埃及和意大利南部,并且曾和毕达哥拉斯学派的人接触过,他们引起了他对数学的兴趣.因此柏拉图的哲学成了数学的哲学,这对他的同时代人和他的继承者有着深远的影响.
回到雅典后,柏拉图在城郊的一个树林中创办了一所学园,世人称之为柏拉图学园.为了使学生绝不怀疑他对数学的重视,他叫人在校门口挂上一块字牌,禁止不懂几何学的学生入内.
和毕达哥拉斯一样,柏拉图也认为打开宇宙之谜的钥匙是数和形.对他来说,神不断在从事几何作图,因此在研究哲学之前首先必须研究几何学.所以我们发现他对严谨性是明显地加以强调的.鉴于毕达哥拉斯学派在其对点、线等的定义上所遭遇到的困难,他就着手去澄清这些基础本质.点不再是构成平面和立体图形的基本“砖块”了,点只是线之端,线是面之界,等等.柏拉图有许多定义,也可能有一两条公理曾被欧几里得采纳到他的《几何原本》中.
虽然柏拉图的主要兴趣是在几何学,但他对算术即关于数的科学也极为重视.在他的著作中,特别是在《理想国》一书中,他热烈主张这门学科具有极大的提高思维能力的作用.确定构成直角三角形的一组线段的长度的一种最早的系统性方法,应当归功于他.他曾指出,其长度以数字$(n^2-1)$,$2n$和$(n^2+1)$表示的三条线段构成直角三角形.他还发展了分析的证明方法,来代替希腊人所常用的综合法.在分析法中,假定结果是真的,而研究者以此作为出发点,推论到一个已经确立了的真理.因此这种方法是否有效要看各个分析步骤是否可逆.
在柏拉图学园的有力影响下,数学继续得到了发展.学园对数学发展的推动作用是很大的,它的主要传统就是更加注意严谨.雅典的泰阿泰德(公元前$480$年前后)是苏格拉底的弟子,学园的一个重要人物,对不尽根的理论作出了贡献.他还写了一本关于五种正立方体的著作.他是否已能证明仅仅存在五种正立方体,这还不能肯定,但要相信他是能证明的,否则就不会有什么需要他去发现的了,因为完全可以肯定这五种立方体远在更早的时候就已为人所知.欧几里得《几何原本》第十卷中的主题有很多地方应归功于泰阿泰德.属于后期毕达哥拉斯学派的塔伦图姆的阿契塔表现对基本平面几何和立体几何的异常精通.他还研究力学,这是希腊人所一直忽视的.阿契塔又想出了一种用两条相交曲线解决倍立方问题的巧妙方法.
柏拉图学园里最著名的人物之一,就是尼多斯地区的欧多克索斯(公元前$408-$前$355$).他发展了一般的比例理论,并且把它加以推广,使之包括一种新型的数——无理数.他在这个问题上的大部分工作已被欧几里得收集到《几何原本》第五卷中.他发展了穷竭法,这在数学进展中同样是重要的.这项成就使他在微积分的发明中享有很高声誉.他用这种方法证明了圆锥体和棱锥体的体积各为同高和同底的圆柱体和棱柱体体积的三分之一.这种在希腊数学中曾经起过重要作用的方法是十分严谨的,它的基础是欧几里得在其《几何原本》第十卷开头所说明的那条公理.由于避免了关于无限小的困难,使得欧多克索斯能以希腊人可以接受的方法提出他的论证,这就是他对普及这种方法的贡献.直到晚近,数学家找到了麻烦较少的方法以后,才放弃使用这种方法.
柏拉图死后,学园的领导人是柏拉图的侄儿,雅典的彪西波,后来是加尔西顿的色诺克拉底,两人都是有名的数学家.他们的工作主要是把已经知道了的东西加以系统化,很少引进新方法.学园成立后的整个时期,是一个非常重要和丰富多彩的时期.学园的影响延续了好几百年,这主要是由于它的成员们的热忱.事实上,一直到公元$529$年查士丁尼皇帝认为它是异说的中心而下令封闭它以后,柏拉图所创设的这个学园才停止了活动.
这里必须提一下亚里士多德(公元前$384-$前$322$),他是柏拉图学园里的学生,是一位真正渊博的学者.虽然他主要不是一个数学家,但他极为重视数学,由于他人们才了解公理、公设和定义之间的明显区别.他对无限大和连续性也有明确的见解.他对当时的欧多克索斯和其他几何学家的著作似乎都很熟悉,在他的著作中发现有许多重要的几何学定理,例如:多边形的外角之和等于四直角;在包围给定面积的所有平面图形中,以圆的周长为最小.在力学方面,他提出了某些原理,这些原理虽然是错误的,却一直保持到$16$世纪.
亚历山大学派
在公元前$338$年喀罗尼亚战役中,马其顿的腓力使雅典人一败涂地,从此雅典城再也没能复兴起来.两年后腓力去世,由其子亚历山大大帝继位.新国王立即着手征服已知的世界.公元前$332$年,他侵吞了埃及,在尼罗河畔建立了亚历山大城.他在九年之后去世,接着便是大混乱和内讧.广阔和国土被他的将领们所分割,在分赃中,埃及落在一个绰号叫做“救世主”的托勒密手中.和亚历山大一样,托勒密也在亚里士多德门下学习过,并且似乎也从老师那里学到了好学精神.他把亚历山大定为国都,在他的影响下,亚历山大很快成为古代世界的文化中心和商业中心.在这里建立起了现代大学的前身、著名的博物馆及宏伟的图书馆.艺术和科学都受到热情的培育.公元$641$年亚历山大遭到了阿拉伯人的洗劫.在此之前的一段时期,为时几达千年,它一直是无可争辩的学术中心.
当时许多学者都为这座繁荣的城市所吸引,其中有三个人决定了此后数百年数学的进程.首先是欧几里得.由于他,几何学从一团没有联系和未予严谨证明的定理变成了一座建立在巩固基础上的巍峨大厦.不到$100$年以后,阿基米德和阿波罗尼奥斯又把几何学提高到无可超越的水平,直到$17$世纪为止.
关于这些先驱者的生平,人们确实知道得很少.从《欧德摩斯摘要》一书中,我们得知欧几里得大约是在公元前$300$年崭露头角的,而他赖以成名的《几何原本》一书,大约是在公元前$320$年编成.这本著作是如此著名,以致我们只须略作一下介绍.一直到现代,它还被认为是研究几何学的入门书.
《几何原本》一书是从一系列定义、公设和“共同概念”开始的,这些“共同概念”后来被称为公理或自明真理.原先只有$5$条公设,头$3$条是关于作图的.这$3$条公设是:
$1$.连接两点可以作一直线.
$2$.直线的两端可以任意延长.
$3$.可以作一圆,具有给定的中心和给定的半径.
第四条公设是说所有的直角都相等.第五条是欧几里得赖以建立其全部关于平行线的理论的基础,这个公设指出:“如果一条直线落在另外两个直线上,且在割线一侧所成之两内角之和小于二直角,那么,只要在小于二直角的这两个内角所在的割线那一侧延长这两条直线,它们就会相交.”
欧几里得试图根据这些定义、公理和公设,以绝对严谨的方式建立起几何学知识的整个大厦.在他以前,也有人设想过同样的计划,但是正如《欧德摩斯摘要》一书中所说,“把几何学原理联系到一起,把欧多克索斯的许多定理有次序地安排起来,把泰阿泰德的许多定理加以完善化,并对前人未经严谨证明的许多东西给以无可争辩的阐明”的,乃是欧几里得.
《几何原本》第一卷所讨论的,是关于直线和由线段构成的平面图形的几何学.第二卷建立了许多人所共知的代数恒等式.由于没有代数符号,希腊人只能依靠几何学方法证明它们.这两卷的内容很少是毕达哥拉斯学派所不知道的.

欧几里得对这一定理的证明:等腰三角形的两底角相等,若再延长相等的两边,则在底边另一侧的两角也相等.引自巴罗著《欧几里得》一书.(蒙皇家学会赐予转载)
第三卷讨论圆的性质,其中有许多在哲人派试图解决求圆面积问题时就已发现了.第四卷继续讨论圆的几何学,特别提到了某些圆内接和圆外切的直线图形方面的问题.命题$10$指出了如何作一等腰三角形,使其每一底角均为第三角的两倍.这个命题是毕达哥拉斯学派早已知道的,他们曾利用它来作成正五边形.在使用这种方法时,要按照中末比来分割(黄金分割)一条线段,这肯定也是毕达哥拉斯学派所知道的.
第五卷详细探讨了关于比例的理论,并且把它推广到各种量,此外还证明了它既可以应用到可通约的量,也可以应用到不可通约的量.希思认为,希腊数学中没有什么发现比这个理论更能令人夸耀了.
$\mathrm{Heach},Greek\; Mathematics,$第一卷,$384$页.
一般认为,该卷中大部分是欧多克索斯和泰阿泰德的工作,但是把它们编排得合乎逻辑次序,应该归功于欧几里得.书中关于比值和比例的基本概念是这样定义的:
各个量在被乘时仍能保持各量间的相应比数称为彼此间有一比值.(定义$4$)
所谓成等比的诸量,如第一量与第二量之比等于第三量与第四量之比,是指在以任何等倍数乘第一量与第三量,并以任何等倍数乘第二量和第四量时,前者的等倍数必相同地大于,或相同地等于,或相同地小于后者的相应的等倍数.(定义$5$)
成等比的诸量称为比例量.(定义$6$)
第六卷把第五卷中已经建立起来的关于比例的一般理论应用到平面图形上去.
第七、八、九卷与算术即数的理论有关.单位的定义是,用它把每个存在的事物称为一.奇数和偶数、素数和合数、平方数和立方数、完全数等都有了定义,例如一个完全数就是“等于它的各部分之和的数”,即等于它的所有因子(包括$1$)之和的数.第七卷中的命题$1$指出,“若在两个不等数中,每当从大数中尽可能地减去小数,再从小数中尽可能地减去所得余数,又从前一余数中尽可能地减去下一余数,如此下去,并且任何余数都不是前一余数的约数,直至达到$1$为止,则此二给定数互为素数”.这个命题是用归谬法来证明的,从它可以得出求不是互素的两个或三个数的最大公约数的方法.第七卷的其余部分讨论素数的性质,其中包含下列命题:
$1$.若两数对任一数为素数,则它们的积对该数也为素数.(第七卷,命题$24$)
$2$.若两数互为素数,则两数之和对两数中任何一数也互为素数,又若两数之和对两数各为素数,则原来两数互为素数.(第七卷,命题$28$)
$3$.任一合数均可用某个素数相约.(第七卷,命题$31$)
$4$.任何数要么是素数,要么可以用某个素数相约.(第八卷,命题$32$)
最后七个命题导出求两个或两个以上数的最小公倍数的方法.
第八卷主要是研究有关连比例数的定理.该卷指出如何在两个数之间插入若干几何中项,并且证明了:如果两个数$a$与$b$之比等于另外两个数$c$与$d$之比,且$a$与$b$之间有$n$个几何中项,则在$c$与$d$之间也有$n$个几何中项.欧几里得还证明了:
$1$.如果一系列数成连比,则它们的平方、立方等也成连比.(第八卷,命题$13$)
$2$.在两个平面数(即平方数)中,只存在一个几何中项,而在两个立体数(即立方数)中,只存在两个几何中项.
$3$.如果三个数成连比,而第一个数是平方数,则第三个数也是平方数.(第八卷,命题$22$)
$4$.如果四个数成连比,且第一数是立方数,则第四个数也是立方数.(第八卷,命题$23$)
第九卷继续讨论第八卷中的问题.该卷发展了素数的理论,并且指出素数的个数是无限的.“素数比任何指定的数目都多.”(第九卷,命题$20$)命题$8$是一个有趣的定理:“若从$1$起有任意多个数成连比例,则从单位数起,第$3$,第$5$,第$7\cdots \cdots $个数是平方数,而第$4$,第$7$,第$10\cdots \cdots $个数是立方数.若从单位数起有任意多个数成连比例,而紧接着单位数的是一个平方数(或立方数),则其余的数都是平方数(或立方数).但如果在该系列数中,第一个数后面的不是平方数,那就只有第$3$,第$5$,第$7\cdots \cdots $个数是平方数.又如果第一个数后面的不是立方数,那就只有第$4$,第$7$,第$10\cdots \cdots $个数都是立方数”(第九卷,命题$10$)接着便是后来闻名于算术界的一个基本定理:一个数能以一种方式并且只能以一种方式分解为若干素因数的乘积.欧几里得是这样来说明这个重要定理的:“如果一个数是能以若干素数通约的最小数,则除了原来的素数以外,它将不能用其他任何素数相约.”(第九卷,命题$14$)命题$35$提出了一种巧妙方法来求几何级数的和:如果有任意多个数成连比例,并且第二个数与最后一个数都可以减去第一个数,则第二个数的增量与第一个数之比,将等于最后一个数的增量与最后一个数前面的所有数之和的比.例如,若级数是
$$a_1 ,a_2 ,a_3 ,\cdots ,a_n ,a_{n+1} $$
且
$$\dfrac{a_{n+1} }{a_n } =\dfrac{a_n }{a_{n-1} } =\cdots =\dfrac{a_2 }{a_1 } $$
即
$$\dfrac{a_{n+1} -a_n }{a_n } =\dfrac{a_n -a_{n-1} }{a_{n-1} } =\cdots =\dfrac{a_2 -a_1 }{a_1 } $$
现在,如果有任意多个数成连比例,则由于任一前项与后项之比等于所有前项的和与所有后项的和之比(第七卷,命题$22$),故将所有前项与所有后项相加,即得:
$$\dfrac{a_{n+1} -a_1 }{a_n +a_{n-1} +\cdots +a_1 } =\dfrac{a_2 -a_1 }{a_1 } $$
从这个关系即可确定$S_n $,即$a_1 +a_2 +a_3+\cdots +a_n $.但欧几里得实际上没有用这个方法来求几何级数的和,而是用它来建立确定完全数的法则,命题$36$说明了这个法则:如果从单位开始有任意多个数连续成倍比,直到所有各数之和成为素数,并将这个和乘以最末数得出某数,则乘积一定是完全数,亦即如果下一和式是素数:
$$1+2+2^2+2^3+\cdots +2^n $$
则
$$(1+2+2^2+2^3+\cdots +2^n)2^n $$
是完全数.例如,$1+2+4+8+16=31$,那么$31$是素数.因此$31\times 16$或$496$是完全数.$496$的因数是$1,2,4,8,16,31,62,124,248$,它们之和是$496$,这证明上述法则是正确的.

欧几里得对其书中$\mathrm{X} ,1$的证明引自巴罗:$Euclidr’s\; Elementorum\;Libri\;XV,Breviter\;Demonstrata$一书.(蒙皇家学会赐予转载)
第十卷是讨论无理数,通常认为这一卷是欧几里得的杰作.德$\cdot $摩根认为第十卷最为完美,远非其他各卷甚至第五卷所能比拟.该卷内容大都属于泰阿泰德的工作,但也要归功于欧几里德,因为他把整个内容按逻辑次序编排了起来.该卷一开始就给可通约数与不可通约数、有理直线和无理直线等下了定义.“能为同一约数相约的数称为可通约数,不能有任何共同约数的数称为不可通约数.”(定义$1$)“如有若干直线,若以每一直线为边构成的诸正方形能以同一面积相约,则此诸直线称为平方可通约直线;而如果这些正方形不可能用任何面积来通约,则此诸直线称为平方不可通约直线.”(定义$2$)在这些定义下,欧几里得证明了与给定直线可通约与不可通约的直线分别有无限多条,其中有些只是本身与这条给定直线可通约或不可通约,其他一些则是本身及其平方都能与这条直线通约或不可通约.“如果给定一直线称为有理直线,则与它可通约的所有直线,不论是本身及其平方同时与它可通约,或仅仅是其平方与它可通约,都称为有理直线;而所有本身或平方不能与它通约的直线,称为无理直线.”(定义$3$)
希思爵士曾经很清楚地解释过这里所用名词的意义.“‘平方可通约的’这一术语相当于泰阿泰德称之为平方根亦即不尽根的意思.如果$a$是任一直线,则$a$和$a\sqrt{m} $或$a\sqrt{m} $和$a\sqrt{n} $($m,n$都是整数,或约至最简的算术分数,可为真分数,亦可为假分数,但非平方数)是只能平方可通约的.按照欧几里得的说法,所有本身可通约的直线,也是平方可通约的,但不是所有平方可通约的直线都能本身可通约.另一方面,平方不可通约的直线一定也是本身不可通约的,但不是所有本身不可通约的直线都平方不可通约.事实上,只能平方可通约的直线,本身是不可通约的,但显然不是平方不可通约.有理的:我们可以取任一直线并称之有理的,然后相对这条取为有理的直线,把其他直线或称为无理的,或称为无理的.对于欧几里得来说,不仅一条本身可与一有理直线通约的直线是有理的,而且一条只能与一有理直线平方可通约的直线也是有理的.那就是说,若$P$是一有理直线,并且$m$和$n$是整数,$\dfrac{m}{n} $是最简分数而非平方数,则不仅$\dfrac{m}{n} \cdot P$是有理的,而且$\sqrt{\dfrac{m}{n} } \cdot P$也是有理的$\cdots \cdots $无理直线在欧几里得看来乃是本身及其平方都不能与所取有理直线通约的.若$K$不是平方数,则$\sqrt{K} \cdot a$就不是无理的.”(希思:《欧几里得》,第三卷,$11\sim 12$页.)
命题$1$提供了穷竭法的基础,这种方法早就为欧多克索斯用过,但到了欧几里得,他已能随心所欲地用它.这个问题可说明如下:取两个不等量,若从大量中减去一个大于或等于它本身一半的量,再从余量中减去大于或等于这余量一半的量,并且不断重复这一程序,则最后剩下的,将是一个比所取二量中较小的一个还要小的最.他的证明如下.
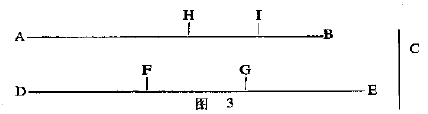
令$AB$与$C$(图$3$)为二给定的不等量,$AB$大于$C$,同时$C$的某一倍数大于$AB$.令$DE$是$C$的倍数,它大于$AB$.将$DE$分成几部分$DF$,$FG$,$GE$,各与$C$相等.从$AB$割去大于它本身一半的$AH$,再从剩下的$HB$割去大于本身之一半的$HI$,这样不断继续下去,直到$AB$的分段数目与$DE$的分段数目相等.
设$AH$,$HI$,$IB$为$AB$的分段,其段数与$DF$,$FG$,$GE$的段数相等.由于$DE$大于$AB$,并从$DE$已经割去了小于其一半的$EG$,从$AB$已经割去了大于其一半的$AH$,所以剩下来的$GD$大于剩下来的$HB$.
因为$GD$大于$HB$,并且从$GD$已经割去了其一半,即$FG$,从$HB$已经割去了大于其一半的$HI$,由此可知剩下来的$DF$大于剩下来的$IB$.但$DF$等于$C$,故$C$大于$IB$,即$IB$小于$C$,亦即剩下来的量小于给定二量中较小的量,这就是所要证明的.
我们将看到,欧几里得要靠这个定理来证明(第十二卷,命题$2$)诸圆的面积之比等于各以它们的直径为边所作的正方形的面积之比.他还立即在接着的一个命题里应用了这个定理,作为他检验两个量是否可通约的方法的基础.这个命题是:若取二不等量,不断地依次从大量减去小量,并且剩下的永远不能与它前面的量相约,则此二量不可通约.再下面的两个命题指出如何确定两个或三个量的最大公约数.确定的方法使人想起第七卷命题$2$、命题$3$中所用的方法,那个方法是确定两个或三个数的最大公约数的.
往下的$4$个命题讨论可通约量和不可通约量的性质.可通约量彼此之比应可表为一个数与另一数的比;而当二量之比可以表为一个数与另一数的比时,这两个量就可通约.(第十卷,命题$5$、$6$)不可通约的量彼此不能表为一个数与另一数之比;而当两个量彼此不能表为一个数与另一数之比时,这两个量就不可通约.(第十卷,命题$7$、$8$)由此可以证明(第十卷,命题$9$):以本身可通约的诸直线为边所作的正方形,彼此之间的比可表为一个平方数与另一平方数之比;而正方形彼此之间的比若能表为一个平方数与另一平方数之比,则它们的边也就是本身可通约的.但以本身不可通约的诸直线为边所作的正方形,彼此之间的比不能表为一个平方数与另一平方数之比;而当诸正方形彼此之间的比不能表为一个平方数与另一平方数之比时,它们的边就不是本身可通约的.这个定理的证明要归功于泰阿泰德.
命题$10$指出如何求出两条直线与给定的直线不可通约,其中一条仅仅是本身与它不可通约,另一条同时还与它平方不可通约.命题$11$则证明了,如有$4$个量成比例,并且第$1$个量与第$2$个量可通约,则第$3$个量与第$4$个量也可通约;若第$1$个量与第$2$个量不可通约,则第$3$个量与第$4$个量也不可通约.因此我们就有一个定理,若以代数语言来表示,这个定理就是:二次方程$ax-x^2=\dfrac{1}{4} b^2 $的根与$a$能否通约,要看$\sqrt{a^2-b^2} $与$a$能否通约.
接着就是对无理直线加以精密分类,这一工作是从命题$21$开始的.命题$21$说:只能平方可通约的诸有理直线所围成的长方形是无理的,与之相等的正方形之边也是无理的.后者可称为中位量的.在其后的命题中,欧几里得研究了可以表为$\sqrt{\sqrt{a} \pm \sqrt{b} } $的各种可能直线,其中$a$和$b$表示两条可通约的直线.命题$28$的一个引理指出如何求两个平方数,使它们的和也是一个平方数;另一个引理指出如何求两个平方数,使它们的和不是平方数.
第十一卷至第十三卷专门讨论立体几何学.第十一卷把平面直线和平面角的几何学推广到平面和平面所构成的角上.立体角的定义是由两个以上的平面角所包围的角,这些平面角不在同一平面内,但都是从同一点作出的.由此可以证明:$1$.若一立体角是由三个平面角包围而成,则其中任何两个角之和大于第三角.$2$.构成任何一立体角的诸平面角之和小于四直角.该卷的其余部分讨论了立体图形的性质,其中有平行六面体、圆锥体、球体.后两种立体图形被定义为旋转体.因此球的定义就不是与一固定点成等距离的空间诸点的轨迹,而是使一个半圆的直径保持固定,把这个半圆绕转一周而回到其初始运动的位置时,这样描出的图形就是球.和他的许多继承者一样,欧几里得所认识到的唯一的圆锥体乃是直圆锥体.由于这种立体图形在圆锥曲线几何中起着重要作用,所以我们把欧几里得对它所下定义全文引出:“使直角三角形的一条直角边保持固定,把这个三角形旋转一周并回到其初始运动的位置,这样描出的图形就是圆锥体.而当保持固定的直角边等于旋转一周运动的一条直角边时,这圆锥体就是直角圆锥体;如果小于该直角边,它就是钝角圆锥体;如果大于该直角边,它就是锐角圆锥体.”(定义$18$)
第十二卷中自由地使用了穷竭法.它被用来证明:
$1$.诸圆之内接相似多边形彼此之比,等于在诸直径上作出的的正方形彼此之比.(命题$1$)
$2$.诸圆彼此之比,等于其在其直径上作出的正方形之比.(命题$2$)
$3$.底面为三角形,高相同的诸棱锥体彼此之比,等于它们的底之比.(命题$5$)
$4$.同高的圆锥体彼此之比,和同高的圆柱体彼此之比,等于它们的底之比.(命题$11$)
$5$.圆锥体的体积是外接圆柱体体积的三分之一.(命题$10$)
$6$.相似圆锥体(和圆柱体)彼此之比,等于它们的底的直径的三次方之比.(命题$12$)
$7$.诸球彼此之比,等于它们的直径的三次方之比.(命题$18$)
欧几里得对其中第二个命题的证明步骤进行如下:设$ABCD$,$abcd$为二圆;$BD$,$bd$是它们的直径.若圆$ABCD$的面积与圆$abcd$的面积之比不等于$BD^2 $与$bd^2 $之比,则$BD^2$与$bd^2$之比将等于圆$ABCD$与某一大于或小于圆$abcd$的面积之比.
$(1)$设$BD^2$与$bd^2$之比等于圆$ABCD$与一较小面积之比,令此较小面积为$K$.在圆$abcd$内作正方形$abcd$.(图$4$)
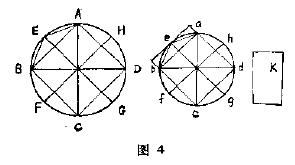
通过$a,b,c,d$各点作圆的切线,于是构成一圆外切正方形,并且它的面积将是正方形$abcd$的面积的二倍.
但由于圆的面积小于其外切正方形的面积,所以内接正方形的面积大于圆$abcd$的面积的一半.
现在将弧$ab$,$bc$,$cd$,$da$如在$e,f,g,h$处平分,并连接$ae$,$eb$,$bf$,$fc$,$cg$,$gd$,$dh$,$ha$.在$e$点作切线,于是在$ab$上完成了一个长方形.
这长方形的面积是三角形$abe$的两倍,由于弓形$aeb$小于这长方形,所以三角形$abe$大于弓形$aeb$的一半,同理,对于弓形$bfc$等等也有类似结果.
现在,如果把剩下的诸弧例如$ae$再予以一部分,并且再把它们的中点同$a$和$e$这些点连接起来,最后就会得到一些弓形,其面积小于圆$abcd$的面积与面积$K$之差.因此按照第十卷中的命题$1$,所得到的多边形$aebfcgdh$就大于面积$K$.现在再在圆$ABCD$内作内接多边形$AEBFCGDH$,它与多边形$aebfcgdh$相似.
于是多边形$AEBFCGDH$的面积$\colon $多边形$aebfcgdh$的面积$=BD^2 \colon bd^2 $.(第十二卷,命题$1$)
但$BD^2 \colon bd^2 =$圆$ABCD\colon K$
因此圆$ABCD\colon K=$多边形$AEBFCGDH\colon $多边形$aebfcgdh$
所以圆$ABCD\colon $多边形$AEBFCGDH=K\colon $多边形$aebfcgdh$
但因为圆$ABCD$大于其内接多边形,所以面积$K$大于多边形$aebfcgdh$的面积.
但根据假设,它也小于多边形$aebfcgdh$的面积,因此这是不合理的.
$(2)$通过同样的推理可以证明,圆$ABCD$与一个大于圆$abcd$的面积之比,不可能等于$BD^2$与$bd^2$之比.
第十三卷说明了如何作出五种“球内包的”正方体,即四面体、立方体、八面体、十二面体和二十面体.作这些“球内包的”立体,意思就是求它们的外接球,也就是要建立立体的边(棱)与球的半径之间的关系.欧几里得通过巧妙的推理过程确立了下列结果,其中$r$是球的半径:
四面体的边$=\dfrac{2r\sqrt{6} }{3} $
八面体的边$=r\sqrt{2} $
立方体的边$=\dfrac{2r\sqrt{3} }{3} $
十二面体的边$=r\dfrac{\sqrt{15} -\sqrt{3} }{3} $
二十面体的边$=r\dfrac{\sqrt{10(5-\sqrt{5} )} }{5} $
欧几里得还证明了,“除了上述五种图形外,不可能作出任何其他图形由彼此相等的等边、等角图形所包围”.
第十四卷包括$8$个命题,这一卷只不过是第十卷的补充,人们一直认为它是公元前$2$世纪喜西克利斯的贡献.第十五卷可能是大马士革的工作,价值不大.但通常都把这两卷包括在《几何原本》中.
欧几里得的其他著作
如普罗克洛斯所说,“欧几里得还有其他许多出色的著作,它们都异常精确,充满了科学研究成果”.在欧几里得的其他著作中,属于纯粹几何学方面的唯一留存的著作是《参考书》,这是一本收集了$94$个习题的习题集,目的是要帮助读者获得解题的某些技巧.它对当时的几何学知识宝库并没有增加什么新内容.另一本著作《论除法》已经在$1851$年出版于巴黎的一本阿拉伯教科书中保存下来.$12$世纪时克雷莫那的杰拉德曾把它从阿拉伯文译成拉丁文,这个译本是中世纪的学者所知道的.它所讨论的问题是如何用一条直线把一给定平面图形分割成若干彼此有一定比例(包括相等)的部分.阿基米德还提到过一套四卷本的关于圆锥曲线的著作,它好像已经概括了阿波罗尼奥斯头四本关于圆锥曲线的著作中的大部分题材.欧几里得的其他著作还有《现象学》和《光学》.前者是一本讨论球素几何学的论文集,可能是为了帮助天文学研究而编成的;后者一直保存了下来,也许可以认为它是欧几里得企图建立关于光在球面上反射的基本原理的最早尝试.欧几里得在这本书中已经注意到,前人在平面镜情况下早已认识到入射角和反射角相等的事实,在反射面为球面的情况下仍然正确.
但是,欧几里得的名声仍然是由于《几何原本》这本书.尽管这本书的流传很广,但它不是毫无缺点的,虽然欧几里得涉及到的范围甚广,但有许多重要的命题在书中却找不到.有些重要命题出现在《参考书》中,还有些则为后来的作者所补充了,例如阿波罗尼奥斯和托勒密等人.《几何原本》中没有求积法.各种直线形面积之间的关系(例如平行六面体、棱锥体等)虽然已有清楚地说明,但我们在任何地方都找不到这些图形的面积和体积的表示式.欧几里得虽然证明了圆的面积和它们直径上的正方形的面积成正比,但没有指出如何去求圆的面积,更不用提圆周与直径的比了.
欧几里得的目的是要用一些定义、公理和公设来建立他的几何学的整个结构.第四公设和第五公设无论在古代还是现代都经常受到攻击.人们认为第四公设——所有的直角都相等——可以用重叠法来证明.欧几里得很可能也知道这点.但他如果承认为点,他就得假定几何图形在移动时大小和形状不变,因为他马上在证明两个三角形全等的定理(第一卷,命题$4$)时要用到这个原理.实际上,他在第四公设中所假定的就是几何图形在移动时不变.
著名的平行公设(在现代版本中是公理$12$)也遭到许多批评.从托勒密起,人们一直在尝试证明它,但都失败了.仅当人们了解到可以发明一种证明这条公设无效的几何学时,才放弃了这些尝试.并不是有谁在怀疑这条公设的真理性,重要的是,它并非像一般公理所应有的情形那样是显然自明的.$1733$年,萨凯里决心要“除去欧几里得所有的污点”,他对欧几里得所提解释的健全性具有如此坚强的信念,以致他坚信自己已经获得了成功.晚近,罗巴切夫斯基、黎曼、鲍耶等人也研究过无需平行公理的其他几何学系统问题.
欧几里得给予几何学研究的推动力,在整个公元前$3$世纪主要是由阿基米德和阿波罗尼奥斯保持下来的.但是,关于数论的研究却无人感兴趣,直到将近$400$年后尼科马科斯的出现,才有了对这门学科感兴趣的人.几何学一直吸引着人们注视数学,在不到$100$年中,它甚至已经上升到比欧几里得曾达到过的更高的高峰.
阿基米德
(公元前$287-$前$212$)一直被称为古代最伟大的数学家.他生于叙拉古,但可能在亚历山大学过数学.后来他回到故乡,在那里提出了抗击罗马人进攻的计划,而使他声誉大增.但他自己对于和实际需要有关的发现,却并不怎样重视.他最珍视的是他在纯数学中的发现.
这些发现涉及的范围很广,也说明他对前人在数学中的一切发现具有渊博的知识.在几何学方面,他补充了许多关于平面曲线图形求积法和确定和确定曲面所包围图形的体积方面的独创研究.在这些研究中,他预见到了极微分割的概念,这个概念以后在$17$世纪的数学中起来了非常突出的作用,并且它本身就是微积分的先声.但他缺乏极限的概念.虽然如此,他在研究这些今天要求用微积分来解决的问题上还是获得了若干惊人的成就.在力学方面,他也建立了某些基本原理,并在流体静力学这门学科上进行了开端的工作.
阿基米德著名的理论包括:
$1$.平面平衡$\quad $其中有$15$个命题,它大概是关于力学的最早的科学论文,可以说是力学这门科学的肇始.阿契塔和其他人曾研究过杆杠、尖劈,可能还研究过滑轮,但要是说在阿基米德的论文出现以前,有关原理就已经有了严格的证明,那就太夸大其词了.然而,阿基米德只研究了静力学,他把自己局限在可以归结为杠杆原理(“两个无论是可通约或不可通约的量,在与这两个量成反比的距离处平衡”)的那类问题上,例如确定平面图形和立体图形的重心问题.
$2.$抛物线求积法$\quad $其中有$24$个命题.阿基米德研究了曲线图形求积的问题,并且用穷竭法得到了这样的结果:“任何由直线和直角圆锥体的截面所包围的弓形(即抛物线),其面积都是与其同底同高的三角形面积的三分之四.”
下面是他的论证的稍微简化了一下的译文,可以说明他的研究方法.
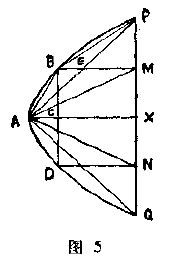
$APQ$是一抛物线弓形,抛物线的顶点为$A$(图$5$).$PQ$交抛物线的轴于$X$点.$PX$和$QX$各在$M$和$N$处平分,作图中所示的各线段就可完成图形.
现在,
$$PX^2 =4MX^2 =4BC^2 $$
$$AX=4AC,$$
因此
$$BM=3AC$$
又
$$EM=\dfrac{1}{2} AX=2AC=2BE$$
因此$\triangle BPE=\dfrac{1}{2} \triangle EPM$和$\triangle BAE=\dfrac{1}{2} \triangle EAM$
所以
$$\triangle BPA=\dfrac{1}{2} \triangle PAM=\dfrac{1}{4} \triangle PAX\label{1} \tag{1} $$
同样可以证明,$\triangle ADQ$是$\triangle AXQ$的$\dfrac{1}{4} $.
用同样方法重复把$PM$,$MX$平分就可证明$\eqref{1}$式的右方加上了一些三角形,其面积等于$\triangle BPA$的$\dfrac{1}{4} $,亦即$\triangle PAX$的$\dfrac{1}{16} $,等等.在这些线上不断这样作下去,就可证明抛物线弓形的面积是
$$\triangle +\dfrac{\triangle }{4} +\dfrac{\triangle }{16} +\dfrac{\triangle }{64} +\cdots $$
这里$\triangle $是指$\triangle APQ$的面积.
如果这个级数延至无限,则不难证明其和是$\dfrac{\triangle }{1-\dfrac{1}{4} } $,或$\dfrac{4\triangle }{3} $.然而阿基米德没有求极限的观念,所以他是用归谬法确立起他的结论的,这种方法在于证明:如果所求面积不等于给定的面积$K$,它就一定同时大于它又小于它.而这是不合理的,由此推知抛物线弓形的面积等于$\triangle APQ$面积的$\dfrac{4}{3} $.阿基米德用权重的办法从力学上证明了这点.
关于阿基米德方法的详尽论述,读者可参考$\mathrm{Heath} ,Greek\;Mathematics$,$Ⅱ,90$页.
$3$.球和圆柱$\quad $分为两卷,总共约有$60$个命题,通常认为这是阿基米德的杰作.开始是一系列定义和$5$个假定,其中主要的几个假定是:
$(1)$在端点相同的所有的线中,线段最短.
$(3)$在周界相同的面中,以那些周界处在平面内的平面为最小.
$(5)$在二不等量中,如将大量超过小量不断加于大量中,可以使其超过任何给定的同类的量.这被称为阿基米德公理.可以明显看出,它类似于欧几里得第五卷中的定义$4$.
由以上可以推知,一个圆内接多边形的周长小于圆周,并且在第$1$命题中证明了,圆外切多边形的周长大于圆周.
这本论著包含了阿基米德最为珍视的发现,其中包括如下几项:
$(1)$任何直圆柱曲面的面积,等于一个圆的面积,这个圆的半径是圆柱高和圆柱底直径之间的比例中项.(命题$13$)
$(2)$圆锥曲面的面积,等于一个圆的面积,这个圆的半径是圆锥母线和圆锥底半径之间的比例中项.(命题$14$)
$(3)$任何球面的面积,是其中最大圆周面积的四倍.(命题$33$)
$(4)$如果在球外外切一个其高等于球直径的圆柱体,则此圆柱的体积等于球体体积的一倍半,其总表面积等于球面面积的一倍半.(命题$33$)
$(5)$球上的任一球截形的表面积,等于一个圆的面积,这个圆的半径等于从球截形顶点到底周上一点所作直线的长度.这与下一定理等价:球截形面积等于一个圆柱曲面的面积,这个圆柱底面的半径与球的半径相同,而高与球截形的高相同.
在对上述命题的证明中,阿基米德已经尽可能地接近了微积分的方法,而没有求助于极限的概念.
$4$.圆的度量$\quad $其中有三个命题:
$(1)$圆的面积等于一个直角三角形的面积,此直角三角形的两个直角边分别等于圆的半径和圆周.
$(2)$圆的面积与其直径上正方形面积之比,近似地等于$11\colon 14$.
$(3)$圆周是直径的三倍大,所大部分小于直径的$\dfrac{1}{7} $,而大于$\dfrac{10}{71} $.他是用$96$边的圆内接正多边形和圆外切正多边形来证明这一点的.
在进行这些证明时,阿基米德避免了用无限小量这个概念,因为这个概念一直是希腊人所怀疑的.他考虑了内接多边形和外切多边形.他确立这个基本原理的方法是说明并证明:“给定二不等量,则不论大量与小量之比如何接近于$1$,都有可能:$(i)$求出两条直线,使得较长的与较短的之比更小(大于$1$);$(ii)$作一圆或扁形的相似外切多边形和内接多边形,使得外切多边形的周长或面积与内接多边形的周长或面积之比小于给定的比.”然后就像欧几里得所做过的那样,他证明如果不断把边数加倍,最后会留下一些弓形,它们加起来比任何指定的面积都要小.阿基米德对此还补充了一点,即指出如果把外切多边形的边数增加到足够多,就能使多边形的面积与圆的面积之差,小于任何给定的面积.
$5$.论螺线$\quad $在某些方面说来,这是阿基米德对数学的全部贡献中最出色的部分.许多作者都在他的作螺线切线的方法中预见到了微积分方法.螺线的定义是这样的:“使直线的一端保持固定,将其以等速在平面中旋转,直至返回原处,同时在直线旋转时,有一点以等速自固定点沿直线移动,这一点在平面上所描出的线就是螺线.”螺线有一个基本性质,把矢径的长度和初始线从初始位置旋转时所通过的角度联系了起来.这个基本性质出现在命题$14$中,现在都以$r=\alpha \theta $这个方程来表示它.阿基米德然后证明了:“在第一个周转和初始线之间所包围的面积,亦即在矢径$0$与$2\pi \alpha $之间所包围的面积,等于半径为$2\pi \alpha $的圆面积的三分之一.”“我认为螺线和回到原处的直线所包的面积,等于以该固定点作中心,以一圈中该点沿直线所描过的长度为半径所作成的圆面积的三分之一.又如有一直线在螺线的末端与螺线相切,并从固定端另作一直线垂直于旋转一周后返回到原处的直线,直至与切线相遇,我认为这样作成的与切线相遇的直线,就等于这个圆的圆周.”
$6$.劈锥曲面和椭球体$\quad $其中包括$40$个命题,是确定由抛物线和双曲线绕其轴旋转而成的立体体积(劈锥曲面)以及椭圆绕其长轴和短轴旋转而成的立体的体积的.在这些命题中,阿基米德自由应用了穷竭法.
$7$.浮体$\quad $这标志着流体静力学这门学科的开端.由于把数学推理应用到浮体的平衡上,阿基米德以公式形式表述了浮体平衡的规律.虽然他宣称轻视机械设计,但他对流体静力学的深入研究使他发明了许多有用的装置,包括著名的扬水机.
$8$.砂计算法$\quad $阿基米德设计出了一种表示大数的计数系统,能表示超出当时流行的希腊计数系统所能表示的范围的数,他指出有可以选定一个数,来计数充满整个宇宙的砂数的数目.
除了现存的著作外,据说阿基米德还编写了几本其他著作,它们涉及到的题目很广泛.他的所有名著都以精确和严谨著称,除了欧几里得是一个可能的例外,还找不到任何前人是这样治学的.“这些论著毫无例外地都是数学论文的里程碑.解题计划的逐步启示,命题次序的巧妙排列,严格排除与目的没有直接关联的一切东西,对整体的润饰——其完美性所给人的印象是如此之深,以致于在读者心中能产生一种近乎敬畏的感情.”
$\mathrm{Heath} ,Greek\;Mathematics$,$Ⅱ,92$页.
前面说过,阿基米德一直被称为古代最伟大的学者,可见他的见解已经不可能更现代化了.笛卡儿和牛顿虽不是他的直接继承者,却与他一脉相承.上面我们已经考虑过他在理论和应用两方面对数学的贡献.这些无疑都是重要的,可是这还不足以使我们对他的天才有一种切实的评价.这些与他所促成的方法比较起来,都难免要黯然失色,正是他的著作的这一方面,才博得我们最热烈的赞赏.阿基米德对当时的数学细节,表现出一种崇高的漠视态度.只要数学家在作图上受到直尺与圆规的限制,他的眼界就总是有限的.通常都用三角形的边表示其面积的公式归功于希罗,而这个公式对阿基米德来说几乎肯定是知道了的.但对他的同时代人来说,势必要认为它是邪说异端,因为这个公式牵涉到四个长度相乘,而这是同三维欧几里得空间的概念格格不入的.如果阿基米德的继承者能表现出一些像他那样的大胆,丢开三维的限制,那么,数学方面一直到了$18$、$19$世纪才被发现的东西,早就会被发现了.因此阿基米德的见解并不属于亚历山大学派,而应属于牛顿甚至高斯学派.
帕尔加的阿波罗尼奥斯
我们从阿基米德转到帕尔加的阿波罗尼奥斯.他以他的天才获得了伟大的几何学家的名声.他约在公元前$255$年生于帕尔加,也在亚历山大学习过,但后来到了帕加马,那里有着亚历山大式的大学和图书馆.
阿波罗尼奥斯是在几何学中运用综合法的卓越能手.他的名声是靠《圆锥曲线》($Conic\; Sections$)一书得来的,该书共有八卷,但希腊原文中只有四卷保存下来.在中世纪发现了另外三卷的阿拉伯文译本,后来哈雷曾尝试根据他对帕普斯《数学汇编》($Mathematical\;Collections$)的研究材料重编第八卷.在保存下来的几卷中,很少有什么是早期几何学家所不知道的.例如,有人认为它们和遗失掉的欧几里得论圆锥曲线的书没有实质上的不同.
通常都认为圆锥曲线的发现应当归功于梅内赫莫斯(公元前$350-$约前$300$),他在尝试解决倍立方问题时,曾用双曲线和抛物线相交或两条抛物线相交的办法求得了这个问题的解.阿波罗尼奥斯的先辈,包括梅内赫莫斯在内,都把圆锥曲线看成是由垂直一母线的平面截割直圆锥面而得到的截线.我们说过,欧几里得和他的追随者只熟悉直圆锥面,而要产生三种不同的圆锥曲线,就要用三种不同的锥面,它们的不同在于产生它们的三角形的顶角不同.在阿波罗尼奥斯以前,一般认为圆锥曲线是锐角锥面的、直角锥面或钝角锥面的截线.具体情况要看轴线和母面之间的角是小于、等于还是大于直角的一半.阿波罗尼奥斯放弃了这种描述不同圆锥曲线的方法.与此不同,他采取了一个决定性步骤,就是证明它们都能从同一个锥面(不论是直角锥面或斜面)得到,它们都是平行于或以任何角度倾斜于锥面的一个斜边的截线.这样,上述名称就不再有什么意义,而被阿波罗尼奥斯代之以椭圆、抛物线和双曲线的名称.
抛物线一词早为阿基米德所用.
如以$p$代表曲线的参数(正焦弦),$d$代表相应的直径,并且曲线是以直径和直径一端的切线来作轴,那么,阿波罗尼奥斯的定义就可用笛卡儿坐标表示为下列方程:
$y^2=px$抛物线
$y^2=px+\dfrac{px^2}{d} $双曲线
$y^2=px-\dfrac{px^2}{d} $椭圆
有人认为阿波罗尼奥斯熟悉坐标系的基本原理,这是极可疑的.然而有一件事也许可以肯定:假如他已掌握了这种方法,他就不会在这方面留下多少东西让费马和笛卡儿去发现了.
头四卷书具有引论的性质.由于阿波罗尼奥斯否定了当时公认的圆锥曲线定义,并决定把它们看成是任一直锥面或斜锥面的平面截线,所以第一卷是从锥面或锥式曲面的定义开始的.
他说,设有一个圆以及在圆平面外有一固定点.这固定点一般并不落在通过圆心垂直于圆平面的直线上.现在通过固定点作一直线,使它与圆周相接,然后使它旋转,但在旋转中永远保持与圆周相接.这样的线在两个两个方向上延长,就会得出一个锥式曲面.它是由两个面所组成的,这两个面彼此顶对着,并在固定点相遇,这固定点就称为顶点.通过这固定点到圆心作一直线,此直线称为轴.
从这样一个面得出三种圆锥曲线的方法,在第一卷的命题$11$到$14$中有所描述.接着是说明和证明这些曲线的主要性质.阿波罗尼奥斯无论在哪里都没有运用圆锥曲线的焦点-次线性质,他是引用直径来确立那些性质的.直径的定义是:一条平分所有平行于一给定直线的曲线弦的直线.第二卷开始是描述渐近线的性质.其中指出:由于渐近线是向无限远伸展,所以他们要与曲线越来越靠近,以致于它们相隔的距离可以小于任何给定的长度.此外还证明了,由曲线上任一点向固定方向上的渐近线作直线所围成之矩形,其面积是一定的,这相当于笛卡儿术语中应以方程$xy=c$来表示的关系.接着是描述求圆锥曲线的直径、抛物线的轴、椭圆与双曲线的轴和中心的方法.最后是说明作曲线之切线的各种方法.
第三卷继续讨论同一方面的问题,并且介绍了一些关于轨迹的问题.第四卷主要是讨论关于圆锥曲线相交的定理.第五卷是一本颇见功力之作,讨论的是现代文献中称为法线的有关内容.但是书中并没有把法线看成是垂直于切线的直线,而是看成从曲线的内点或外点所能作到曲线上的最长直线和最短直线.这部分著作以彻底的严密性著称.
阿波罗尼奥斯的盛名完全是靠他的《圆锥曲线》一书.但他还有一些其他著作.帕普斯曾援引一本叫做《截面比》的著作,另一本是《有限截面》,还有一本是《接触点和切线》.最后一本中有个著名的问题:试给定三元素,其中任一元素都可以是一个点、一条直线或一个圆,要求作一圆通过各给定点(如果给定的三元素皆为点的话),或者与给定的各直线或圆相切.根据给定三元素为点、线或圆的各种可能组合,这里共有$10$种不同的问题,其中大多数都是可用初等几何学来解决的.最后一个问题,即作一圆与另外三个圆相切的问题,一直到$17$世纪都使许多数学家为之绞尽脑汁.
阿波罗尼奥斯似乎还有一本论《平面轨迹》的著作.帕普斯也提到这本书.它在数学史中的重要性在于:费马在试图重编他的著作时,曾受到其指引而发现了坐标几何学的原理.
希腊的符号记数法
这里讲一下希腊人所用的记数制是适宜的.除了十进制外,还没有任何关于其他记数制的证据.在最早的时期,希腊人是把数字全部写出来的.但是商业的发展需要有一种表示大数的更简洁的方法,于是逐渐发展起了另外两种记数制度.其中第一种是以单划$1$来代表单位数,它可以重复四次,以表示$1$到$4$.$5$是用一个新的符号

来表示,这是旧式的$Pente$(五)的第一个字母,它也可以重复四次.同样,$Deka $(十)的第一个字母$\Delta $表示$10$,$H$代表$100$,$X$代表$1\;000$,$M$代表$10\;000$,每个符号都可以重复四次,有时还把这些符号结合起来使用,

和$\Delta $结合起来可以写成

,表示$50$;

表示$500$,

表示$5\;000$,

表示$50\;000$.此外,这种记数法整个是可加的,各个符号是并排写的,大数写在前面,如$\triangle 111$代表$13$.通常认为这种记数方法是雅典的方法,因为雅典的碑文上常使用它.它通行于公元前$500$年至公元前$100$左右.
这种记数方法随后又逐渐为另一种使用希腊字母的方法所代替.头$9$个字母代表$1$到$9$,其次$9$个字母代表$10$到$90$,最后$9$个字母代表$100$到$900$.由于希腊字母只有$24$个,因此从腓尼基字母借用了三个字$vau$,$koph$和$sampi$来补充,分别代表$6$,$90$和$900$.这样就可以一直表示到数字$999$.至于从千数起到$9\;000$是使用单位数的记号加上一撇,例如$’A$代表$1\;000$.为了区别代表数目的字母与文字字母,他们使用了各种方法.有时是用点放在数字的两旁,更经常的是用一横画加在表示数字的字母上面.这种方法整个也是可加的.希腊人和古代大多数民族一样,还没有关于位置值的知识.
这种方法可能比它以前的更简洁,但是使用如此之多的不同符号,必然要给通常的算术运算带来很大困难.况且,它也模糊了数字之间的简单关系,例如奇数和偶数之间的区别.
公元前$3$世纪末,希腊数学史中最光辉的时期就此终止.欧几里得、阿基米德、阿波罗尼奥斯把数学带到了这样一种境界:除非设计出一种进步得多的记数方法,否则就不可能有什么发展了.虽然在以后的年代里,一直没有出现过可与上面几位相比拟的数学家,但也不是完全没有.有些人的贡献也不是不重要的.他们的著作保存下来的不多,因此我们只能依靠赛翁、亚历山大的帕普斯、普罗克洛斯和欧托基奥斯等人的评论.但就整个来说,他们的著作中很少出现独创之外.数学研究的方向逐渐转到实用方面,而不是理论探讨方面了.大约在公元前$2$世纪左右,狄奥克莱斯发明了一种曲线,叫做蔓叶线,这使他求出了两条直线之间的两个比例中项.他的同时代人尼科马卡斯发现了蚌线,用来解决倍立方问题.
在公元$200$年左右享有盛名的亚历山大的希罗,表示出卓越的数学天才,但他所继承的是埃及传统,而不是希腊传统.他的功绩在于发明许多巧妙的力学装置,但通常认为发现用三角形三边表示其面积的公式的也是他.这个公式是$\sqrt{s(s-a)(s-b)(s-c)} $,他在他的《几何学》一书中对此给出了几何证明.阿基米德看来也知道这个公式.希罗在这本著作中还研究了正多边形的求积法.有一部分专门讨论解二次方程的有关问题,其中一个典型问题是:已知一圆的直径、周长及面积之和,试分别决定它们.
希罗的解法如下:假定已知的和是$212$.将它乘以$154$,乘积是$32\;648$.这个数加上$841$,其和是$33\;489$.现在取其平方根($=183$).从这个平方根减去$29$,余数是$154$.这个数的$\dfrac{1}{11} $是$14$,这就是圆的直径.为了求出圆周,要从$183$中减去$29$,余数$154$,倍之得到$308$.这个数的$\dfrac{1}{7}$是$44$,这是周长.在求面积时,是以周长$44$乘直径$14$,乘积为$616$.这个数的$\dfrac{1}{4}$,即$154$就是圆的面积.直径、周长及面积之和是$212$.
如果把希罗的解法现代化,那就是设$d$为直径,并假定圆周与直径之比为$22\colon 7$,而面积是$(\dfrac{11}{14} )d^2$,我们有
$$d+(\dfrac{22}{7} )d+(\dfrac{11}{14} )d^2 =212$$
或
$$(\dfrac{11}{14} )d^2 +(\dfrac{29}{7} )d=212$$
希罗用$154$去乘,使得第一项成为平方数.这给出
$$121d^2+638d=32\;648$$
两端加上$29^2$即$841$而成完全平方:
$$121d^2+638d+841=32\;648+841=33\;489$$
即
$$(11d+29)^2=33\;489$$
$$11d+29=183$$
因而
$$d=14$$
由此不难得到圆周和面积.
这本著作中还有一个求非平方数的平方根近似值的有趣方法.在确定三角形的同时,希罗考虑的是一个其边为$7$,$8$,$9$的图形.他用他的公式求得的面积是$\sqrt{720}$.由于$720$的平方根不是有理数,所以希罗就取一个最接近于$720$的平方数,这就是$729$即$27^2$.然后他将$720$除以$27$,得$26\dfrac{2}{3} $;加上$27$,得$53\dfrac{2}{3} $;其一半$26\dfrac{5}{6}$非常接近于$720$的平方根.
如$A$是一非平方数,$a^2$是最接近于$A$的平方数,与它只差一个量$b$,亦即$A=a^2+b$,则在一级近似下,$\sqrt{A} =a(1+\dfrac{b}{2a^2} )$.
尼西亚的喜帕恰斯(公元前$120$年左右)主要是一位天文学家,精确确定一年长短的就是他,此外他还解释了岁差现象.他在天文学方面的研究,使他创立了一门崭新的学科-三角学.他没有什么著作保存下来,但据亚历山大学派的赛翁说,他曾编过一本$12$卷的著作,可以认为是这门学科的基础.托勒密无疑曾利用过他来制定他的弦数表.下文将叙述这一点.

