初等超越函数的极限计算

三角函数的极限计算

这里与前面的极限计算题不同之处是：在一般教科书中列为最基本的两个函数极限之一，即

$$\lim_{x\to 0} \dfrac{\sin{x} }{x} =1,\label{1} \tag{1.31} $$

起重要作用.它是比较三角函数与标准无穷小量的基础.此外，在本小节的许多习题的计算中，等价量代换法也是基本的.关于它的简单介绍见$\S 1.5.7$之$1$.

求下列极限：

$471$.$\displaystyle \lim_{x\to 0} \dfrac{\sin{5x} }{x} $.

解$\quad \displaystyle \lim_{x\to 0} \dfrac{\sin{5x} }{x} =5\lim_{x\to 0} \dfrac{\sin{5x} }{5x} =5\cdot 1=5$.

$472$.$\displaystyle \lim_{x\to \infty } \dfrac{\sin{x} }{x} $.

解$\quad $当$x\to \infty $时，$\dfrac{1}{x} $为无穷小量，而$\vert \sin{x} \vert \leqslant 1$，故$\dfrac{\sin{x} }{x} $当$x\to \infty $时为无穷小量，即$\displaystyle \lim_{x\to \infty } \dfrac{\sin{x} }{x} =0$.

$473$.$\displaystyle \lim_{x\to \pi } \dfrac{\sin{mx} }{\sin{nx} } $.

解$\quad $令$x=\pi +y$，则当$x\to \pi $时，$y\to 0$.于是，

$$\begin{align}
& \lim_{x\to \pi } \dfrac{\sin{mx} }{\sin{nx} } \\
= & \lim_{y\to 0} \dfrac{(-1)^m \sin{my} }{(-1)^n \sin{ny} } \\
= & (-1)^{m-n} \lim_{y\to 0} \left( \dfrac{\sin{my} }{my} \cdot \dfrac{ny}{\sin{ny} } \cdot \dfrac{m}{n} \right) \\
= & (-1)^{m-n} \dfrac{m}{n} .
\end{align}$$

$474$.$(a)\displaystyle \lim_{x\to 0} \dfrac{1-\cos{x} }{x^2} ;(b)\lim_{x\to 0} \dfrac{\tan{x} }{x} ;(c)\lim_{x\to 0} x\cot{3x} $.

解$\quad (a)$首先要看出这是$\dfrac{0}{0} $型的不定式.然后用三角公式如下进行：

$$\lim_{x\to 0} \dfrac{1-\cos{x} }{x^2} =\lim_{x\to 0} \dfrac{2\sin{}^2 \dfrac{x}{2} }{x^2} =\dfrac{1}{2} \lim_{x\to 0} \left( \dfrac{\sin{\dfrac{x}{2} } }{\dfrac{x}{2} } \right)^2 =\dfrac{1}{2} .$$

注$\quad $为便于今后的引用，重记为

$$\lim_{x\to 0} \dfrac{1-\cos{x} }{x^2} =\dfrac{1}{2} \label{474.1} \tag{1.32} $$

利用极限理论中的等价量记号（见$\S 1.5.7$之$1$），我们就得到了两个重要的等价无穷小量的公式：

$$\sin{x} \sim x(x\to 0),1-\cos{x} \sim \dfrac{1}{2} x^2 (x\to 0).\label{474.2} \tag{1.33} $$

$(b)$

$$\lim_{x\to 0} \dfrac{\tan{x} }{x} =\lim_{x\to 0} \dfrac{\sin{x} }{x} \cdot \dfrac{1}{\cos{x} } =\lim_{x\to 0} \dfrac{\sin{x} }{x} \cdot \dfrac{1}{\displaystyle \lim_{x\to 0} \cos{x} } =1.$$

$(c)$

$$\lim_{x\to 0} x\cot{3x} =\dfrac{1}{3} \lim_{x\to 0} \dfrac{3x}{\sin{3x} } \cdot \cos{3x} =\dfrac{1}{3} \lim_{x\to 0} \dfrac{3x}{\sin{3x} } \cdot \lim_{x\to 0} \cos{3x} =\dfrac{1}{3}.$$

$475$.$\displaystyle \lim_{x\to 0} \dfrac{\tan{x} -\sin{x} }{\sin{}^3 x } $.

解

$$\begin{align}
& \lim_{x\to 0} \dfrac{\tan{x} -\sin{x} }{\sin{}^3 x } \\
= & \lim_{x\to 0} \dfrac{\dfrac{\sin{x} }{\cos{x} } -\sin{x} }{\sin{}^3 x } \\
= & \lim_{x\to 0} \dfrac{1-\cos{x} }{\cos{x} \sin{}^2 x } \\
= & \lim_{x\to 0} \dfrac{2\sin{}^2 \dfrac{x}{2} }{4\sin{}^2 \dfrac{x}{2} \cos{}^2 \dfrac{x}{2} \cos{x} } \\
= & \lim_{x\to 0} \dfrac{1}{2\cos{}^2 \dfrac{x}{2} \cos{x} } \\
= & \dfrac{1}{2} .
\end{align}$$

$476$.$\displaystyle \lim_{x\to 0} \dfrac{\sin{5x} -\sin{3x} }{\sin{x} } $.

解$1\quad $第一步是看出这是$\dfrac{0}{0} $型的不定式，然后按照等价量代换法，分母可以用$x$代替，然后分式的极限可以分成两项分别处理.由于这是第一次用等价量代换法，我们将上述过程详细写出如下，其中三次使用了极限$\eqref{1} $：

$$\begin{align}
& \lim_{x\to 0} \dfrac{\sin{5x} -\sin{3x} }{\sin{x} } \\
= & \lim_{x\to 0} \left( \dfrac{\sin{5x} -\sin{3x} }{x} \cdot \dfrac{x}{\sin{x} } \right) \\
= & \lim_{x\to 0} \left( \dfrac{\sin{5x}}{5x} \cdot 5-\dfrac{\sin{3x}}{3x} \cdot 3\right) \\
= & 5-3 \\
= & 2 .
\end{align}$$

解$2\quad $用三角函数的和差化积公式也可以如下求解：

$$\lim_{x\to 0} \dfrac{\sin{5x} -\sin{3x} }{\sin{x} } =\lim_{x\to 0} \dfrac{2\cos{4x} \sin{x} }{\sin{x} } =2\lim_{x\to 0} \cos{4x} =2.$$

$477$.$\displaystyle \lim_{x\to 0} \dfrac{\cos{x} -\cos{3x} }{x^2} $.

解$\quad $这是$\dfrac{0}{0} $型的不定式.利用极限$\eqref{474.1} $即可计算如下：

$$\begin{align}
& \lim_{x\to 0} \dfrac{\cos{x} -\cos{3x} }{x^2} \\
= & \lim_{x\to 0} \left( \dfrac{\cos{x} -1 }{x^2} + \dfrac{1-\cos{3x} }{9x^2 } \cdot 9\right) \\
= & \dfrac{1}{2} (-1+9)\\
= & 4 .
\end{align}$$

$478$.$\displaystyle \lim_{x\to 0} \dfrac{1+\sin{x} -\cos{x} }{1+\sin{px} -\cos{px} } $.

解$\quad $这是$\dfrac{0}{0} $型的不定式.分子分母同除以$x$后再利用等价关系$\eqref{474.2} $可计算如下：

$$\lim_{x\to 0} \dfrac{1+\sin{x} -\cos{x} }{1+\sin{px} -\cos{px} } =\lim_{x\to 0} \dfrac{\dfrac{\sin{x} }{x} +\dfrac{1-\cos{x} }{x^2} \cdot x}{\dfrac{\sin{px} }{x} +\dfrac{1-\cos{px} }{x^2} \cdot x} =\dfrac{1}{p} .$$

$479$.$\displaystyle \lim_{x\to \frac{\pi }{4} } \tan{2x} \tan{\left( \dfrac{\pi }{4} -x\right) }$.

解$\quad $令$y=\dfrac{\pi }{4} -x$，则

$$\begin{align}
& \lim_{x\to \frac{\pi }{4} } \tan{2x} \tan{\left( \dfrac{\pi }{4} -x\right) } \\
= & \lim_{x\to \frac{\pi }{4} } \dfrac{\sin{2x} \sin{\left( \dfrac{\pi }{4} -x\right) } }{\cos{2x} \cos{\left( \dfrac{\pi }{4} -x\right) } } \\
= & \lim_{y\to 0} \dfrac{\cos{2y} \sin{y} }{\sin{2y} \cos{y} } \\
= & \lim_{y\to 0} \dfrac{\cos{2y} }{2\cos{}^2 y} \\
= & \dfrac{1}{2} .
\end{align}$$

$480$.$\displaystyle \lim_{x\to 1} (1-x)\tan{\dfrac{\pi x}{2} } $.

解$\quad $设$y=1-x$，则

$$\begin{align}
& \lim_{x\to 1} (1-x)\tan{\dfrac{\pi x}{2} } \\
= & \lim_{y\to 0} y\cot{\dfrac{\pi y}{2} } \\
= & \lim_{y\to 0} \left( \dfrac{\dfrac{\pi y}{2}}{\sin{\dfrac{\pi y}{2} } } \cdot \dfrac{2}{\pi } \cdot \cos{\dfrac{\pi y}{2} }\right) \\
= & \dfrac{2}{\pi } .
\end{align}$$

学过连续性和导数的读者不难看出，习题$481$就是证明$\sin{x} $，$\cos{x} $，$\tan{x} $的连续性，而习题$482-487$就是计算$6$个三角函数的导数.

$481$.证明等式：

$\displaystyle (a)\lim_{x\to a} \sin{x} =\sin{a} $；$\displaystyle (b)\lim_{x\to a} \cos{x} =\cos{a} $；

$\displaystyle (c)\lim_{x\to a} \tan{x} =\tan{a} \left( a\neq \dfrac{2n-1}{2} \pi ;n=0,\pm 1,\pm 2,\cdots \right) $.

证$\quad $先建立一个不等式：当$0 < x < \dfrac{\pi }{2} $时有

$$\sin{x} < x < \tan{x} .\label{481.1} \tag{1} $$

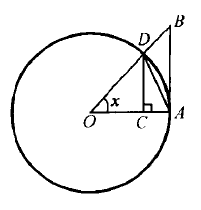
事实上，在如图的单位圆内，当$0 < x < \dfrac{\pi }{2} $时，显然有

$$S_{\triangle OAD} < S_{扇形OAD} < S_{\triangle OAB} ,$$

即$\dfrac{1}{2} \sin{x} < \dfrac{1}{2} x < \dfrac{1}{2} \tan{x}$，由此立得$\eqref{481.1} $式.

又当$x \geqslant \dfrac{\pi }{2} $时有$\sin{x} \leqslant x < x$，故对一切$x > 0$都有$\sin{x} < x$；当$x < 0$时，由$\sin{(-x)} < -x$得$-\sin{x} < -x$.综上，我们又得到不等式

$$\vert \sin{x} \vert \leqslant \vert x\vert ,x\in \mathbb{R} ,\label{481.2} \tag{2} $$

其中等号仅当$x=0$时成立.

现证$(a)$.由$\eqref{481.2} $式得

$$\vert \sin{x} -\sin{a} \vert =2\left\vert \cos{\dfrac{x+a}{2} } \right\vert \left\vert \sin{\dfrac{x-a}{2} } \right\vert \leqslant \vert x-a\vert .$$

对任给的$\varepsilon > 0$，只要取$\delta = \varepsilon $，则当$0 < \vert x-a\vert < \delta $时，就有

$$\vert \sin{x} -\sin{a} \vert < \varepsilon .$$

所以$\displaystyle \lim_{x\to a} \sin{x} =\sin{a} $.

$(b)\displaystyle \lim_{x\to a} \cos{x} =\lim_{x\to a} \sin{\left( \dfrac{\pi }{2} -x\right) } =\sin{\left( \dfrac{\pi }{2} -a\right) } =\cos{a} $.

$(c)\displaystyle \lim_{x\to a} \tan{x} =\lim_{x\to a} \dfrac{\sin{x} }{\cos{x} } =\dfrac{\displaystyle \lim_{x\to a} \sin{x} }{\displaystyle \lim_{x\to a} \cos{x} } =\dfrac{\sin{a} }{\cos{a} } =\tan{a} $.其中$a\neq \dfrac{2n-1}{2} \pi ;n=0,\pm 1,\pm 2,\cdots $.

求下列极限：

$482$.$\displaystyle \lim_{x\to a} \dfrac{\sin{x} -\sin{a} }{x-a} $.

解$1\quad $三角公式（和）差化积也可看作因式分解.用此法可把函数之差转化为自变量之差，以便比较.如下所示，本题将从分子中析出的$\sin{\dfrac{x-a}{2} } $与分母$x-a$的比归结为基本极限$\displaystyle \lim_{t\to 0} \dfrac{\sin{t} }{t} $，从而解答本题.具体计算如下：

$$\lim_{x\to a} \dfrac{\sin{x} -\sin{a} }{x-a} =\lim_{x\to a} \dfrac{2\cos{\dfrac{x+a}{2} } \sin{\dfrac{x-a}{2} } }{x-a} =\cos{a} .$$

解$2\quad $用三角函数的和角公式同样可以达到目的：

$$\lim_{x\to a} \dfrac{\sin{(a+(x-a))} -\sin{a} }{x-a} =\lim_{x\to a} \dfrac{\sin{a} [\cos{(x-a)} -1]+\cos{a} \sin{(x-a)} }{x-a} =\cos{a} .$$

其中同时使用了$\eqref{1} $和$\eqref{474.1}$.

$483$.$\displaystyle \lim_{x\to a} \dfrac{\cos{x} -\cos{a} }{x-a} $.

解$\quad $仿习题$482$的解$2$，有

$$\lim_{x\to a} \dfrac{\cos{(a+(x-a))} -\cos{a} }{x-a} =\lim_{x\to a} \dfrac{\cos{a} [\cos{(x-a)} -1]-\sin{a} \sin{(x-a)} }{x-a} =-\sin{a} .$$

$484$.$\displaystyle \lim_{x\to a} \dfrac{\tan{x} -\tan{a} }{x-a} $.

解$1\quad $若将正切函数化为正弦和余弦函数来做，则有

$$\begin{align}
& \lim_{x\to a} \dfrac{\tan{x} -\tan{a} }{x-a} \\
= & \lim_{x\to a} \dfrac{\dfrac{\sin{x} }{\cos{x} } -\dfrac{\sin{a} }{\cos{a} } }{x-a} \\
= & \lim_{x\to a} \dfrac{\sin{x} \cos{a} -\sin{a} \cos{x} }{(x-a)\cos{x} \cos{a} } \\
= & \lim_{x\to a} \dfrac{\sin{(x-a)} }{(x-a)\cos{x} \cos{a} } \\
= & \dfrac{1}{\cos{}^2 a} .
\end{align}$$

解$2\quad $为了处理分子可以利用恒等式$\tan{(x-a)} =\dfrac{\tan{x} -\tan{a} }{1+\tan{x} \tan{a} } $，于是得到

$$\tan{x}-\tan{a} =\tan{(x-a)} (1+\tan{x} \tan{a} ) ,$$

它可看作正切的差化积，其所起作用与习题$482$相同.以下计算已经不难：

$$\begin{align}
& \lim_{x\to a} \dfrac{\tan{x} -\tan{a} }{x-a} \\
= & \lim_{x\to a} \dfrac{\tan{(x-a)} }{x-a} (1+\tan{x} \tan{a} ) \\
= & 1+\tan{}^2 a\\
= & \sec{}^2 a .
\end{align}$$

$485$.$\displaystyle \lim_{x\to a} \dfrac{\cot{x} -\cot{a} }{x-a} $.

解$\quad $将余切函数化为正弦和余弦函数来做，则有

$$\begin{align}
& \lim_{x\to a} \dfrac{\cot{x} -\cot{a} }{x-a} \\
= & \lim_{x\to a} \dfrac{\dfrac{\cos{x} }{\sin{x} } -\dfrac{\cos{a} }{\sin{a} } }{x-a} \\
= & \lim_{x\to a} \dfrac{\sin{a} \cos{x} -\sin{x} \cos{a} }{(x-a)\sin{x} \sin{a} } \\
= & -\lim_{x\to a} \dfrac{\sin{(a-x)} }{(a-x)\sin{x} \sin{a} } \\
= & -\dfrac{1}{\sin{}^2 a} .
\end{align}$$

$486$.$\displaystyle \lim_{x\to a} \dfrac{\sec{x} -\sec{a} }{x-a} $.

解$\quad $将正割函数化为正弦和余弦函数来做，则有

$$\begin{align}
& \lim_{x\to a} \dfrac{\sec{x} -\sec{a} }{x-a} \\
= & \lim_{x\to a} \dfrac{\dfrac{1}{\cos{x} } -\dfrac{1 }{\cos{a} } }{x-a} \\
= & \lim_{x\to a} \dfrac{\cos{a} -\cos{x} }{(x-a)\cos{x} \cos{a} } \\
= & \lim_{x\to a} \left( \dfrac{\sin{\dfrac{x+a}{2} }}{\cos{x} \cos{a} } \cdot \dfrac{\sin{\dfrac{x-a}{2} } }{\dfrac{x-a}{2} }\right) \\
= & \dfrac{\sin{a} }{\cos{}^2 a} .
\end{align}$$

$487$.$\displaystyle \lim_{x\to a} \dfrac{\csc{x} -\csc{a} }{x-a} $.

解$\quad $将余割函数化为正弦和余弦函数来做，则有

$$\begin{align}
& \lim_{x\to a} \dfrac{\csc{x} -\csc{a} }{x-a} \\
= & \lim_{x\to a} \dfrac{\dfrac{1}{\sin{x} } -\dfrac{1 }{\sin{a} } }{x-a} \\
= & \lim_{x\to a} \dfrac{\sin{a} -\sin{x} }{(x-a)\sin{x} \sin{a} } \\
= & -\lim_{x\to a} \left( \dfrac{\sin{a} -\sin{x} }{a-x } \cdot \dfrac{1}{\sin{x} \sin{a} }\right) \\
= & -\dfrac{\cos{a} }{\sin{}^2 a} .
\end{align}$$

注$\quad $在微分学中将习题$482-487$中的$\dfrac{\sin{x} -\sin{a} }{x-a} $，$\dfrac{\cos{x} -\cos{a} }{x-a} ,\cdots $分别称为正弦，余弦$\cdots $从$a$到$x$的（一阶）差商.它们的极限$(x\to a)$分别是正弦，余弦$\cdots $的导数.

可以看到，有些题用合适的三角函数公式来演化确实很方便（例如习题$476$的解$2$）.问题在于对于较复杂的题，演化的结果有时会出现大量的三角函数，这时继续做下去就可能会有困难，甚至陷入繁复的计算中而“不能自拔”.例如，学过高阶导数的读者一定会发现，后面的习题$488-492$涉及前$4$个三角函数的二阶导数问题.这时直接用三角函数变换来计算就可能比较复杂.

与上两个小节一样，我们还是建议在函数极限计算中以无穷小量的阶数分析和等价量代换法为主要思路（例如$\eqref{474.2}$，习题$476$的解$1$和习题$477-478$的解等）.在这里我们提出下列命题，它可以解决本小节中较复杂习题的极限计算.虽然它不可能对每一个题提供最好的解法，但至少可以提供相当有效的解法.

命题$1.8\quad $设$a$为给定常数，则有

$(1)\displaystyle \lim_{x\to 0} \dfrac{x-\sin{x} }{x^2} =0$；

$(2)\displaystyle \lim_{x\to 0} \dfrac{\sin{(a+x)} -\sin{a} -x\cos{a} }{x^2} =-\dfrac{\sin{a} }{2} $；

$(3)\displaystyle \lim_{x\to 0} \dfrac{\cos{(a+x)} -\cos{a} +x\sin{a} }{x^2} =-\dfrac{\cos{a} }{2} $；

$(4)\displaystyle \lim_{x\to 0} \dfrac{\tan{(a+x)} -\tan{a} -x\sec{}^2 a }{x^2} =\sec{}^2 a\tan{a} =\dfrac{\sin{a} }{\cos{}^3 a} $；

$(5)\displaystyle \lim_{x\to 0} \dfrac{\cot{(a+x)} -\cot{a} +x\csc{}^2 a }{x^2} =\csc{}^2 a\cot{a} =\dfrac{\cos{a} }{\sin{}^3 a} $.

证$\quad (1)$由于分子为奇函数，只要对$x > 0$作证明即可.利用导出$\eqref{1} $时大多数教科书都已经证明的不等式

$$\sin{x} < x < \tan{x} \left( 0 < x < \dfrac{\pi }{2} \right) ,$$

也就是$\cos{x} < \dfrac{\sin{x} }{x} < 1$，即可得到

$$0 < \dfrac{x-\sin{x} }{x^2} =\dfrac{1}{x} \left( 1-\dfrac{\sin{x} }{x} \right) < \dfrac{1}{x} (1-\cos{x} ) =\dfrac{1}{x} \cdot 2\sin{}^2 \dfrac{x}{2} < \dfrac{1}{x} \cdot \dfrac{x^2}{2} =\dfrac{x}{2} ,$$

令$x\to 0$就知道$\displaystyle \lim_{x\to 0} \dfrac{x-\sin{x} }{x^2} =0$.（实际上已经得到$\sin{x} =x+O(x^3)(x\to 0)$.）

$(2)$中令$a=0$就得到$(1)$，因此是它的推广.利用$(1)$可作如下推导得到$(2)$：

$$\begin{align}
& \lim_{x\to 0} \dfrac{\sin{(a+x)} -\sin{a} -x\cos{a} }{x^2} \\
= & \lim_{x\to 0} \dfrac{\sin{a} \cos{x} +\cos{a} \sin{x} -\sin{a} -x\cos{a} }{x^2} \\
= & \lim_{x\to 0} \left( \dfrac{\sin{a} (\cos{x} -1)}{x^2} + \dfrac{\cos{a} (\sin{x} -x)}{x^2}\right) \\
= & -\dfrac{\sin{a} }{2} .
\end{align}$$

$(3)$利用$(1)$可作如下推导得到$(3)$：

$$\begin{align}
& \lim_{x\to 0} \dfrac{\cos{(a+x)} -\cos{a} +x\sin{a} }{x^2} \\
= & \lim_{x\to 0} \dfrac{\cos{a} \cos{x} -\sin{a} \sin{x} -\cos{a} +x\sin{a} }{x^2} \\
= & \lim_{x\to 0} \left( \dfrac{\cos{a} (\cos{x} -1)}{x^2} - \dfrac{\sin{a} (\sin{x} -x)}{x^2}\right) \\
= & -\dfrac{\cos{a} }{2} .
\end{align}$$

$(4)$利用$(1)$可推导如下：

$$\begin{align}
& \lim_{x\to 0} \dfrac{\tan{(a+x)} -\tan{a} -x\sec{}^2 a }{x^2} \\
= & \lim_{x\to 0} \dfrac{\dfrac{\sin{(a+x)} }{\cos{(a+x)} } -\dfrac{\sin{a} }{\cos{a} } -\dfrac{x}{\cos{}^2 a} }{x^2} \\
= & \lim_{x\to 0} \dfrac{\dfrac{\sin{x} }{\cos{(a+x)} \cos{a} } -\dfrac{x}{\cos{}^2 a} }{x^2} \\
= & \lim_{x\to 0} \dfrac{\cos{a} \sin{x} -x\cos{(a+x)} }{\cos{(a+x)} \cos{}^2 a \cdot x^2} \\
= & \dfrac{1}{\cos{}^3 a} \lim_{x\to 0} \left( \dfrac{\cos{a} (\sin{x} -x)}{x^2} + \dfrac{\cos{a} -\cos{(a+x)} }{x} \right) \\
= & \dfrac{1}{\cos{}^3 a} \lim_{x\to 0} \dfrac{\cos{a} -\cos{(a+x)} }{x} \\
= & \dfrac{\sin{a} }{\cos{}^3 a} .
\end{align}$$

注$1\quad $上述证明的最后一步即是《习题集》中的习题$483$，它的求解与习题$482$的解$2$相同，当然也可以用和差化积公式来做.建议读者自行完成上述命题中的$(3)$和$(5)$的证明，它们比不少习题还容易一些.此外，$(4)$的证明也可以仿照习题$484$的解$2$进行.

$(5)$利用$(1)$可推导如下：

$$\begin{align}
& \lim_{x\to 0} \dfrac{\cot{(a+x)} -\cot{a} +x\csc{}^2 a }{x^2} \\
= & \lim_{x\to 0} \dfrac{\dfrac{\cos{(a+x)} }{\sin{(a+x)} } -\dfrac{\cos{a} }{\sin{a} } +\dfrac{x}{\sin{}^2 a} }{x^2} \\
= & \lim_{x\to 0} \dfrac{\dfrac{-\sin{x} }{\sin{(a+x)} \sin{a} } +\dfrac{x}{\sin{}^2 a} }{x^2} \\
= & \lim_{x\to 0} \dfrac{-\sin{a} \sin{x} +x\sin{(a+x)} }{\sin{(a+x)} \sin{}^2 a \cdot x^2} \\
= & \dfrac{1}{\sin{}^3 a} \lim_{x\to 0} \left( \dfrac{-\sin{a} (\sin{x} -x)}{x^2} + \dfrac{-\sin{a} +\sin{(a+x)} }{x} \right) \\
= & \dfrac{1}{\sin{}^3 a} \lim_{x\to 0} \dfrac{-\sin{a} +\sin{(a+x)} }{x} \\
= & \dfrac{\cos{a} }{\sin{}^3 a} .
\end{align}$$

注$2\quad $利用大$O$和小$o$记号，命题$1.8$的结论可改写为以下形式：

$$\sin{x} =x+O(x^3)(x\to 0);$$

$$\sin{(a+x)} =\sin{a} +x\cos{a} -\dfrac{\sin{a} }{2} x^2+o(x^2) (x\to 0);$$

$$\cos{(a+x)} =\cos{a} -x\sin{a} -\dfrac{\cos{a} }{2} x^2+o(x^2) (x\to 0);$$

$$\tan{(a+x)} =\tan{a} +x\sec{}^2 a +(\sec{}^2 a \tan{a} ) x^2+o(x^2) (x\to 0);$$

$$\cot{(a+x)} =\cot{a} -x\csc{}^2 a +(\csc{}^2 a \cot{a} ) x^2+o(x^2) (x\to 0).$$

其中$o(x^2)$是当$x\to 0$时高于二阶的无穷小量.（已学过微分学的读者自然会看出，这$4$个公式就是写出到二阶项的带佩亚诺余项的泰勒公式，也称为局部泰勒公式.）

用命题$1.8$可方便地解决习题$481-491$的极限计算.

$488$.$\displaystyle \lim_{x\to 0} \dfrac{\sin{(a+2x)} -2\sin{(a+x)} +\sin{a} }{x^2} $.

解$\quad $分子是正弦函数的二阶差分，利用命题$1.8$的注$2$中的公式直接计算分子如下：

$$\begin{align}
& \sin{(a+2x)} -2\sin{(a+x)} +\sin{a} \\
= & [\sin{(a+2x)} -\sin{(a+x)} ]-[\sin{(a+x)} -\sin{a} ] \\
= & [x\cos{(a+x)} -\dfrac{\sin{(a+x)} }{2} x^2] -[x\cos{a} -\dfrac{\sin{a} }{2} x^2] +o(x^2) \\
= & x[\cos{(a+x)} -\cos{a} ]-\dfrac{x^2}{2} [\sin{(a+x)} -\sin{a} ]+o(x^2) \\
= & -x^2 \sin{a} +o(x^2) (x\to 0),
\end{align}$$

可见本题的答案是$-\sin{a} $.

$489$.$\displaystyle \lim_{x\to 0} \dfrac{\cos{(a+2x)} -2\cos{(a+x)} +\cos{a} }{x^2} $.

解$\quad $分子是余弦函数的二阶差分，利用命题$1.8$的注$2$中的公式直接计算分子如下：

$$\begin{align}
& \cos{(a+2x)} -2\cos{(a+x)} +\cos{a} \\
= & [\cos{(a+2x)} -\cos{(a+x)} ]-[\cos{(a+x)} -\cos{a} ] \\
= & [-x\sin{(a+x)} -\dfrac{\cos{(a+x)} }{2} x^2] -[x\sin{a} -\dfrac{\cos{a} }{2} x^2] +o(x^2) \\
= & -x[\sin{(a+x)} -\sin{a} ]-\dfrac{x^2}{2} [\cos{(a+x)} -\cos{a} ]+o(x^2) \\
= & -x^2\cos{a} +o(x^2) (x\to 0),
\end{align}$$

可见本题的答案是$-\cos{a} $.

$490$.$\displaystyle \lim_{x\to 0} \dfrac{\tan{(a+2x)} -2\tan{(a+x)} +\tan{a} }{x^2} $.

解$\quad $与习题$488$用同样的方法计算其分子如下：

$$\begin{align}
& \tan{(a+2x)} -2\tan{(a+x)} +\tan{a} \\
= & [\tan{(a+2x)} -\tan{(a+x)} ]-[\tan{(a+x)} -\tan{a} ] \\
= & [x\sec{}^2 (a+x)+\sec{}^2 (a+x)\tan{(a+x)} x^2] -[x\sec{}^2 a+(\sec{}^2 a\tan{a} )x^2 ] +o(x^2) \\
= & x[\sec{}^2 (a+x) -\sec{}^2 a]+[\sec{}^2 (a+x)\tan{(a+x)} -\sec{}^2 a\tan{a} ]x^2 +o(x^2) \\
= & x[\tan{}^2 (a+x)-\tan{}^2 a]+o(x^2) \\
= & x^2 (2\tan{a} \sec{}^2 a)+o(x^2) (x\to 0),
\end{align}$$

可见本题的答案是$2\tan{a} \sec{}^2 a $.

$491$.$\displaystyle \lim_{x\to 0} \dfrac{\cot{(a+2x)} -2\cot{(a+x)} +\cot{a} }{x^2} $.

解$\quad $与习题$488$用同样的方法计算其分子如下：

$$\begin{align}
& \cot{(a+2x)} -2\cot{(a+x)} +\cot{a} \\
= & [\cot{(a+2x)} -\cot{(a+x)} ]-[\cot{(a+x)} -\cot{a} ] \\
= & [-x\csc{}^2 (a+x)+\csc{}^2 (a+x)\cot{(a+x)} x^2] -[-x\csc{}^2 a+(\csc{}^2 a\cot{a} )x^2 ] +o(x^2) \\
= & -x[\csc{}^2 (a+x) -\csc{}^2 a]+[\csc{}^2 (a+x)\cot{(a+x)} -\csc{}^2 a\cot{a} ]x^2 +o(x^2) \\
= & -x[\cot{}^2 (a+x)-\cot{}^2 a]+o(x^2) \\
= & x^2 (2\cot{a} \csc{}^2 a)+o(x^2) (x\to 0),
\end{align}$$

可见本题的答案是$2\cot{a} \csc{}^2 a $.

再举出用命题$1.8$的弱化形式解决问题的例子.

$492$.$\displaystyle \lim_{x\to 0} \dfrac{\sin{(a+x)} \sin{(a+2x)} -\sin{}^2 a }{x} $.

解$\quad $用$\sin{(a+x)} =\sin{a} +x\cos{a} +O(x^2) (x\to 0)$和$\sin{(a+2x)} =\sin{a} +2x\cos{a} +O(x^2) (x\to 0)$代入分子就可以得到

$$\lim_{x\to 0} \dfrac{x\sin{a} (\cos{a} +2\cos{a} )}{x} =3\sin{a} \cos{a} .$$

$493$.$\displaystyle \lim_{x\to \frac{\pi }{6} } \dfrac{2\sin{}^2 x+\sin{x} -1}{2\sin{}^2 x-3\sin{x} +1} $.

解

$$\begin{align}
& \lim_{x\to \frac{\pi }{6} } \dfrac{2\sin{}^2 x+\sin{x} -1}{2\sin{}^2 x-3\sin{x} +1} \\
= & \lim_{x\to \frac{\pi }{6} } \dfrac{(\sin{x} +1)(2\sin{x} -1)}{(\sin{x} -1)(2\sin{x} -1)} \\
= & \lim_{x\to \frac{\pi }{6} } \dfrac{\sin{x} +1}{\sin{x} -1} \\
= & -3.
\end{align}$$

$494$.$\displaystyle \lim_{x\to 0} \dfrac{1-\cos{x} \cos{2x} \cos{3x} }{1-\cos{x} } $.

解$\quad $分母为二阶无穷小量.用等价量代换法将分母换为$\dfrac{1}{2} x^2 $，对分子采取递推法即可（参见习题$412$的解$2$）：

$$\begin{align}
& \lim_{x\to 0} \dfrac{1-\cos{x} \cos{2x} \cos{3x} }{1-\cos{x} } \\
= & \lim_{x\to 0} \dfrac{1-\cos{x} +\cos{x} (1-\cos{2x} )+\cos{x} \cos{2x} (1-\cos{3x} )}{1-\cos{x} } \\
= & 1+2\cdot 4\cdot \lim_{x\to 0} \dfrac{1-\cos{2x} }{4x^2} +2\cdot 9\cdot \lim_{x\to 0} \dfrac{1-\cos{3x} }{9x^2} \\
= & 1+8\cdot \dfrac{1}{2} +18\cdot \dfrac{1}{2} \\
= & 14.
\end{align}$$

$495$.$\displaystyle \lim_{x\to \frac{\pi }{3} } \dfrac{\sin{\left( x-\dfrac{\pi }{3} \right) } }{1-2\cos{x} } $.

解$\quad $令$x=\dfrac{\pi }{3} +y$，则

$$\begin{align}
& \lim_{x\to \frac{\pi }{3} } \dfrac{\sin{\left( x-\dfrac{\pi }{3} \right) } }{1-2\cos{x} } \\
= & \lim_{y\to 0} \dfrac{\sin{y} }{1-\cos{y} +\sqrt{3} \sin{y} } \\
= & \lim_{y\to 0} \dfrac{\dfrac{\sin{y} }{y} }{\dfrac{\sin{\dfrac{y}{2} } }{\dfrac{y}{2} } \sin{\dfrac{y}{2}} +\sqrt{3} \dfrac{\sin{y} }{y} } \\
= & \dfrac{\sqrt{3} }{3} .
\end{align}$$

$496$.$\displaystyle \lim_{x\to \frac{\pi }{3} } \dfrac{\tan{}^3 x-3\tan{x} }{\cos{\left( x+\dfrac{\pi }{6} \right) } } $.

解

$$\begin{align}
& \lim_{x\to \frac{\pi }{3} } \dfrac{\tan{}^3 x-3\tan{x} }{\cos{\left( x+\dfrac{\pi }{6} \right) } } \\
= & \lim_{x\to \frac{\pi }{3} } \dfrac{\tan{x} (\tan{}^2 x-3) }{\dfrac{\sqrt{3} }{2} \cos{x} -\dfrac{1}{2} \sin{x} } \\
= & \lim_{x\to \frac{\pi }{3} } \dfrac{\tan{x} (\tan{x} +\sqrt{3} )(\dfrac{\sin{x} }{\cos{x} } -\sqrt{3} ) }{\dfrac{\sqrt{3} }{2} \cos{x} -\dfrac{1}{2} \sin{x} } \\
= & \lim_{x\to \frac{\pi }{3} } -2\tan{x} (\tan{x} +\sqrt{3} )\dfrac{1}{\cos{x} } \\
= & -24.
\end{align}$$

$497$.$\displaystyle \lim_{x\to 0} \dfrac{\tan{(a+x)} \tan{(a-x)} -\tan{}^2 a}{x^2} $.

解

$$\begin{align}
& \lim_{x\to 0} \dfrac{\tan{(a+x)} \tan{(a-x)} -\tan{}^2 a}{x^2} \\
= & \lim_{x\to 0} \dfrac{\left( \dfrac{\tan{a} +\tan{x} }{1-\tan{a} \tan{x} } \right) \left( \dfrac{\tan{a} -\tan{x} }{1+\tan{a} \tan{x} } \right) -\tan{}^2 a}{x^2} \\
= & \lim_{x\to 0} \dfrac{\tan{}^2 x(\tan{}^4 a-1)}{x^2(1-\tan{}^2 x\tan{}^2 a)} \\
= & \tan{}^4 a-1.
\end{align}$$

$498$.$\displaystyle \lim_{x\to \frac{\pi }{4} } \dfrac{1-\cot{}^3 x}{2-\cot{x} -\cot{}^3 x} $.

解

$$\begin{align}
& \lim_{x\to \frac{\pi }{4} } \dfrac{1-\cot{}^3 x}{2-\cot{x} -\cot{}^3 x} \\
= & \lim_{x\to \frac{\pi }{4} } \dfrac{1}{\dfrac{2-\cot{x} -\cot{}^3 x}{1-\cot{}^3 x} } \\
= & \lim_{x\to \frac{\pi }{4} } \dfrac{1}{\dfrac{1-\cot{x} +1-\cot{}^3 x}{1-\cot{}^3 x} } \\
= & \lim_{x\to \frac{\pi }{4} } \dfrac{1}{\dfrac{1}{1+\cot{x} + \cot{}^2 x} +1} \\
= & \dfrac{3}{4} .
\end{align}$$

$499$.$\displaystyle \lim_{x\to 0} \dfrac{\sqrt{1+\tan{x} } -\sqrt{1+\sin{x} } }{x^3} $.

解

$$\begin{align}
& \lim_{x\to 0} \dfrac{\sqrt{1+\tan{x} } -\sqrt{1+\sin{x} } }{x^3} \\
= & \lim_{x\to 0} \dfrac{\tan{x} -\sin{x} }{x^3(\sqrt{1+\tan{x} } +\sqrt{1+\sin{x} } )} \\
= & \lim_{x\to 0} \dfrac{\sin{x} (1-\cos{x} )}{x^3\cos{x} (\sqrt{1+\tan{x} } +\sqrt{1+\sin{x} } )} \\
= & \lim_{x\to 0} \left[ \dfrac{\sin{x} }{x} \cdot \dfrac{(1-\cos{x} )}{x^2} \cdot \dfrac{1}{\cos{x} (\sqrt{1+\tan{x} } +\sqrt{1+\sin{x} } ) } \right] \\
= & \dfrac{1}{4} .
\end{align}$$

$500$.$\displaystyle \lim_{x\to 0} \dfrac{x^2}{\sqrt{1+x\sin{x} } -\sqrt{\cos{x} } } $.

解

$$\begin{align}
& \lim_{x\to 0} \dfrac{x^2}{\sqrt{1+x\sin{x} } -\sqrt{\cos{x} } } \\
= & \lim_{x\to 0} \dfrac{x^2(\sqrt{1+x\sin{x} } +\sqrt{\cos{x} } )}{x\sin{x} +1-\cos{x} } \\
= & \lim_{x\to 0} \dfrac{\sqrt{1+x\sin{x} } +\sqrt{\cos{x} } }{\dfrac{\sin{x} }{x} +\dfrac{1-\cos{x} }{x^2} } \\
= & \dfrac{4}{3} .
\end{align}$$

$501$.$\displaystyle \lim_{x\to 0} \dfrac{\sqrt{\cos{x} } -\sqrt[3]{\cos{x} } }{\sin{}^2 x} $.

解

$$\begin{align}
& \lim_{x\to 0} \dfrac{\sqrt{\cos{x} } -\sqrt[3]{\cos{x} } }{\sin{}^2 x} \\
= & \lim_{x\to 0} \dfrac{\sqrt{\cos{x} } -1+1-\sqrt[3]{\cos{x} } }{\sin{}^2 x} \\
= & \lim_{x\to 0} \dfrac{(\sqrt{\cos{x} } -1 )(\sqrt{\cos{x} } +1)(\cos{x} +1)}{\sin{}^2 x(\sqrt{\cos{x} } +1)(\cos{x} +1)} \\
& +\lim_{x\to 0} \dfrac{(1-\sqrt[3]{\cos{x} } )(1+\sqrt{\cos{x} } +\cos{x} )(1+\cos{x} )}{\sin{}^2 x(1+\sqrt{\cos{x} } +\cos{x} )(1+\cos{x} )} \\
= & -\dfrac{1}{4} +\dfrac{1}{6} \\
= & -\dfrac{1}{12} .
\end{align}$$

$502$.$\displaystyle \lim_{x\to 0} \dfrac{\sqrt{1-\cos{x^2} } }{1-\cos{x} } $.

解

$$\lim_{x\to 0} \dfrac{\sqrt{1-\cos{x^2} } }{1-\cos{x} } =\lim_{x\to 0} \dfrac{\sqrt{\dfrac{1}{2} x^4}}{\dfrac{1}{2} x^2} =\sqrt{2} .$$

$503$.$\displaystyle \lim_{x\to 0} \dfrac{1-\sqrt{\cos{x} } }{1-\cos{\sqrt{x} } } $.

解

$$\lim_{x\to 0} \dfrac{1-\sqrt{\cos{x} } }{1-\cos{\sqrt{x} } } =\lim_{x\to 0} \dfrac{(1-\sqrt{\cos{x} } )(1+\sqrt{\cos{x} } )}{\dfrac{1}{2} x(1+\sqrt{\cos{x} } )} =\lim_{x\to 0} \dfrac{x}{(1+\sqrt{\cos{x} } )} =0.$$

$504$.$\displaystyle \lim_{x\to 0} \dfrac{1-\cos{x} \sqrt{\cos{2x} } \sqrt[3]{\cos{3x} } }{x^2} $.

解

$$\begin{align}
& \lim_{x\to 0} \dfrac{1-\cos{x} \sqrt{\cos{2x} } \sqrt[3]{\cos{3x} } }{x^2} \\
= & \lim_{x\to 0} \dfrac{1-\cos{x} +\cos{x} (1-\sqrt{\cos{2x} } )+\cos{x} \sqrt{\cos{2x} } (1-\sqrt[3]{\cos{3x} } )}{x^2} \\
= & \lim_{x\to 0} \dfrac{1-\cos{x} }{x^2} +\lim_{x\to 0} \dfrac{\cos{x} (1-\sqrt{\cos{2x} } )(1+\sqrt{\cos{2x} } )}{x^2(1+\sqrt{\cos{2x} } )} \\
& +\lim_{x\to 0} \dfrac{\cos{x} \sqrt{\cos{2x} } (1-\sqrt[3]{\cos{3x} } )(1+\sqrt{\cos{3x} } +\cos{3x} )}{x^2(1+\sqrt{\cos{3x} } +\cos{3x} )} \\
= & \dfrac{1}{2} +\dfrac{1\cdot \dfrac{1}{2} \cdot 4}{1+1} +\dfrac{1\cdot 1\cdot \dfrac{1}{2} \cdot 9}{1+1+1} \\
= & 3.
\end{align}$$

$505$.$\displaystyle \lim_{x\to +\infty } (\sin{\sqrt{x+1} } -\sin{\sqrt{x} } )$.

解$\quad $本题并非常见的不定式，但$\sqrt{x+1} -\sqrt{x} $是不定式（见$\S 1.2.1$的习题$47$），且有

$$\sqrt{x+1} -\sqrt{x} =\dfrac{1}{\sqrt{x+1} +\sqrt{x} } \to 0(x\to +\infty ).$$

作正弦的差化积，得

$$\lim_{x\to +\infty } (\sin{\sqrt{x+1} } -\sin{\sqrt{x} } ) =\lim_{x\to +\infty } 2\cos{\dfrac{\sqrt{x+1} +\sqrt{x} }{2} } \sin{\dfrac{\sqrt{x+1} -\sqrt{x} }{2} } =0.$$

幂指函数和对数函数的极限计算

这里的最基本工具是继$\eqref{1}$之后的第二个最基本的函数极限

$$\lim_{x\to 0} (1+x)^{\frac{1}{x} } =e.\label{2} \tag{1.34} $$

与前面从$\eqref{1} $推出$\eqref{474.1} $一样，从$\eqref{2} $可以推出下列几个重要的极限，它们在今后都是不可或缺的基本公式.

$$\lim_{x\to 0} \dfrac{\ln (1+x)}{x} =1,\label{3} \tag{1.35} $$

$$\lim_{x\to 0} \dfrac{a^x -1}{x} =\ln a(a > 0),\lim_{x\to 0} \dfrac{e^x -1}{x}=1,\label{4} \tag{1.36} $$

$$\lim_{x\to 0} \dfrac{(1+x)^{\alpha } -1}{x} =\alpha .\label{5} \tag{1.37} $$

其中$\eqref{3} $即习题$529$，$\eqref{4} $即习题$541$，它在$x=\dfrac{1}{n} $时就是习题$76$，$\eqref{5}$中当$\alpha =\dfrac{1}{n} $时就是习题$444$（也就是公式$(1.30$)）.

用等价记号$\sim $就可以将上述三个公式改写成为$x\to 0$时的等价关系：

$$\ln (1+x) \sim x,a^x-1\sim x\ln a,e^x-1\sim x,(1+x)^{\alpha } -1\sim \alpha x.$$

它们对于使用等价量代换法是非常方便的.

证$\quad $为证明$\eqref{3}$，只要用$\eqref{2}$和对数函数的连续性：

$$\lim_{x\to 0} \dfrac{\ln (1+x)}{x} =\lim_{x\to 0} \ln [(1+x)^{\frac{1}{x} }] =\ln e=1.$$

对于$\eqref{4} $可以先用$\eqref{3} $于$a=e$，这样就可以得到

$$\lim_{x\to 0} \dfrac{e^x -1}{x} =\lim_{x\to 0} \dfrac{e^x -1}{\ln [1+(e^x -1)]} =1,$$

然后对于一般的$a > 0$就有

$$\lim_{x\to 0} \dfrac{a^x -1}{x} =\lim_{x\to 0} \dfrac{e^{x\ln a} -1}{x\ln a} \cdot \ln a=\ln a.$$

最后对于$\eqref{5} $可以用相同的方法推导如下：

$$\lim_{x\to 0} \dfrac{(1+x)^{\alpha } -1}{x} =\lim_{x\to 0} \dfrac{e^{\alpha \ln (1+x)} -1}{\alpha \ln (1+x)} \cdot \dfrac{\ln (1+x)}{x} \cdot \alpha =\alpha .$$

注$\quad $以上的许多推导都涉及复合函数的极限以及若干基本初等函数的连续性.

关于前者，请参看$\S 1.5.7$的第$2$点，其中结合对习题$607$的解答所列出的若干充分条件.

关于后者，则只要用$\S 1.2.9$中的命题$1.4$，并利用沟通数列极限和函数极限之间联系的海涅归结原理，就可以推出幂函数、对数函数、指数函数等的连续性.此外，还可以注意本书中没有讲解的几个题.习题$481$即是求证正弦函数、余弦函数和正切函数的连续性；习题$529$即是求极限$\displaystyle \lim_{x\to 0} \dfrac{\ln (1+x)}{x} $；习题$531$和$548$即是分别计算对数函数和指数函数的导数，这比建立它们的连续性要求更高了.

由此可见，命题$1.4$的代入法对于函数极限同样成立.

举一个具体例子.在$\eqref{3}$的证明中，设$f(y)=\ln y$，$y=g(x)=(1+x)^{\frac{1}{x} } $，则一方面有$\displaystyle \lim_{x\to 0} g(x)=e$，另一方面又利用$f(y)=\ln y$于点$y=e$处连续，这样就可以推出有$\displaystyle \lim_{x\to 0} f(g(x)) =\ln e=1$.

在$\eqref{2} $的基础上可以用下列方法解决许多$1^{\infty } $型的不定式问题.这就是对于$\displaystyle \lim_{x\to a} f(x)=0$，$\displaystyle \lim_{x\to a} g(x)=\infty $的情况，有

$$\lim_{x\to a} (1+f(x))^{g(x)} =\lim_{x\to a} [(1+f(x))^{\frac{1}{f(x)} }]^{(f(x)g(x))} =e^{\lim\limits_{x\to a} (f(x)g(x))} ,\label{6} \tag{1.38}$$

于是只要计算$\lim\limits_{x\to a} (f(x)g(x))$即可.

下面来看一些习题.注意第一步是搞清楚它是否是不定式.如果不是不定式，则一般用代入法即可；如果是不定式，则要根据其类型来采取对策.

$506$.$(a)\displaystyle \lim_{x\to 0} \left( \dfrac{1+x}{2+x} \right)^{\frac{1-\sqrt{x} }{1-x} } $；$(b)\displaystyle \lim_{x\to 1} \left( \dfrac{1+x}{2+x} \right)^{\frac{1-\sqrt{x} }{1-x} } $；$(c)\displaystyle \lim_{x\to +\infty } \left( \dfrac{1+x}{2+x} \right)^{\frac{1-\sqrt{x} }{1-x} } $.

解$\quad $在$(a)$中有$\displaystyle \lim_{x\to 0} \dfrac{1+x}{2+x} =\dfrac{1}{2} $，$\displaystyle \lim_{x\to 0} \dfrac{1-\sqrt{x} }{1-x} =1$，因此只要用代入法就得到极限为$\dfrac{1}{2} $.

在$(b)$中有$\displaystyle \lim_{x\to 1} \dfrac{1+x}{2+x} =\dfrac{2}{3} $，$\displaystyle \lim_{x\to 1} \dfrac{1-\sqrt{x} }{1-x} =\lim_{x\to 1} \dfrac{1}{1+\sqrt{x} } =\dfrac{1}{2} $，因此只要用代入法就得到极限为$\sqrt{\dfrac{2}{3} } $.

在$(c)$中有$\displaystyle \lim_{x\to \infty } \dfrac{1+x}{2+x} =1$，$\displaystyle \lim_{x\to \infty } \dfrac{1-\sqrt{x} }{1-x} =0 $，因此只要用代入法就得到极限为$1^0 =1$.

$507$.$\displaystyle \lim_{x\to \infty } \left( \dfrac{x+2}{2x-1} \right)^{x^2} $.

解$\quad $因为当$x\to \infty $时，有$\displaystyle \lim_{x\to \infty } \dfrac{x+2}{2x-1} =\dfrac{1}{2} $，$\displaystyle \lim_{x\to \infty } x^2 =+\infty $，所以，

$$\lim_{x\to \infty } \left( \dfrac{x+2}{2x-1} \right)^{x^2} =0.$$

$508$.$\displaystyle \lim_{x\to \infty } \left( \dfrac{3x^2-x+1}{2x^2+x+1} \right)^{\frac{x^3}{1-x} } $.

解$\quad $因为当$x\to \infty $时，有$\displaystyle \lim_{x\to \infty } \dfrac{3x^2-x+1}{2x^2+x+1} =\dfrac{3}{2} $，$\displaystyle \lim_{x\to \infty } \dfrac{x^3}{1-x} =-\infty $，所以，

$$\lim_{x\to \infty } \left( \dfrac{3x^2-x+1}{2x^2+x+1} \right)^{\frac{x^3}{1-x} } =0.$$

$509$.$\displaystyle \lim_{n\to \infty } \left( \sin{}^n \dfrac{2n\pi }{3n+1} \right) $.

解$\quad $因为$\left\vert \sin{\dfrac{2n\pi }{3n+1} }\right\vert \leqslant 1$，所以，$\displaystyle \lim_{n\to \infty } \left( \sin{}^n \dfrac{2n\pi }{3n+1} \right) =0$.

$510$.$\displaystyle \lim_{x\to \frac{\pi }{4} +0} \left[ \tan{\left( \dfrac{\pi }{8} +x\right) } \right]^{\tan{2x} } $.

解$\quad $因为当$x\to \dfrac{\pi }{4} +0$时，$1 < \tan{\left( \dfrac{\pi }{8} +x\right) } < +\infty $及$\tan{2x} \to +\infty $，所以$\displaystyle \lim_{x\to \frac{\pi }{4} +0} \left[ \tan{\left( \dfrac{\pi }{8} +x\right) } \right]^{\tan{2x} } =0$.

$511$.$\displaystyle \lim_{x\to \infty } \left( \dfrac{x^2-1}{x^2+1} \right)^{\frac{x-1}{x+1} } $.

解$\quad $因为当$x\to \infty $时，$\displaystyle \lim_{x\to \infty } \dfrac{x^2-1}{x^2+1} =1 $，$\displaystyle \lim_{x\to \infty } \dfrac{x-1}{x+1} =1 $，所以$\displaystyle \lim_{x\to \infty } \left( \dfrac{x^2-1}{x^2+1} \right)^{\frac{x-1}{x+1} } =1$.

$512$.$\displaystyle \lim_{x\to \infty } \left( \dfrac{x^2+1}{x^2-1} \right)^{x^2} $.

解$1\quad $将大括号内的分子分母同除以$x^2$后即可利用$\eqref{2} $如下求极限：

$$\lim_{x\to \infty } \left( \dfrac{x^2+1}{x^2-1} \right)^{x^2} =\lim_{x\to \infty } \left( 1+\dfrac{1}{x^2} \right)^{x^2} \left( 1-\dfrac{1}{x^2} \right)^{-x^2} =e\cdot e=e^2.$$

解$2\quad $这是$1^{\infty } $型的不定式.用$\eqref{6} $的方法就得到

$$\lim_{x\to \infty } \left( 1+\dfrac{2}{x^2-1} \right)^{x^2} =e^{\lim\limits_{x\to +\infty } \frac{2x^2}{x^2-1} } =e^2.$$

解$3\quad $另一种写法是先对于函数取对数，然后用等价量代换法计算极限如下：

$$\lim_{x\to \infty } x^2 \ln \left( \dfrac{x^2+1}{x^2-1} \right) =\lim_{x\to \infty } x^2 \ln \left( 1+\dfrac{2}{x^2-1} \right) =\lim_{x\to \infty } \dfrac{2x^2}{x^2-1} =2,$$

可知极限为$e^2$.其中利用了等价关系$\ln \left( 1+\dfrac{2}{x^2-1} \right) \sim \dfrac{2}{x^2-1} (x\to \infty )$.

注$\quad $解$2$与解$3$本质上完全相同，但对于先取对数的方法还是需要说明一下，因为与幂指函数有关的三个类型的不定式（即$1^{\infty } $，$\infty^0 $和$0^0$）容易从这种方法得到解释.

考虑幂指函数的极限$\displaystyle \lim_{x\to a} u(x)^{v(x)} $，其中设$u(x) > 0$，$x\to a$也可换为其他类型的函数极限.我们要问：这里会遇到什么样的不定式.或者反过来，假设已知存在极限$\displaystyle \lim_{x\to a} u(x)=A$，$\displaystyle \lim_{x\to a} v(x)=B$，其中$A$，$B$允许为非正常极限$\infty $，问上述幂指函数的极限是否可以简单地用代入法得到$A^B$.

用取对数的方法，且同时利用指数函数和对数函数的连续性，就有

$$\lim_{x\to a} u(x)^{v(x)} =e^{\lim\limits_{x\to a} v(x)\ln u(x)} ,$$

其中假设所写出的极限存在.

于是问题已经归结为乘积$v(x)\ln u(x)$当$x\to a$时是否是不定式.由于乘积形式的不定式只可能是$0\cdot \infty $型，从而就只可能出现三种可能性，即$(1)\displaystyle \lim_{x\to a} v(x)=\infty $，$\displaystyle \lim_{x\to a} u(x)=1 $；$(2)\displaystyle \lim_{x\to a} v(x)=0 $，$\displaystyle \lim_{x\to a} u(x)=+\infty $；$(3)\displaystyle \lim_{x\to a} v(x)=0 $，$\displaystyle \lim_{x\to a} u(x)=0 $.回复到幂指函数的极限$\displaystyle \lim_{x\to a} u(x)^{v(x)} $，这就是$1^{\infty } $，$\infty^0 $，$0^0$三种不定式.

需要注意，若$A=\displaystyle \lim_{x\to a} u(x)$为小于$1$的非负数，而$B=\displaystyle \lim_{x\to a} v(x)=\infty $，则极限$\displaystyle \lim_{x\to a} u(x)^{v(x)} $并不是不定式，其中包括容易误认为是不定式的$0^{\infty }$.注意：当指数趋于正无穷大时有$0^{+\infty } =0$；而当指数趋于负无穷大时有$0^{-\infty } =+\infty $.

$513$.$\displaystyle \lim_{x\to \infty } \left( \dfrac{x^2+2x-1}{2x^2-3x-2} \right)^{\frac{1}{x} } $.

解$\quad \displaystyle \lim_{x\to \infty } \left( \dfrac{x^2+2x-1}{2x^2-3x-2} \right)^{\frac{1}{x} } =\lim_{x\to \infty } \left( \dfrac{1}{2} \right)^0 =1$.

$514$.$\displaystyle \lim_{x\to 0} \sqrt[x]{1-2x} $.

解$\quad \displaystyle \lim_{x\to 0} \sqrt[x]{1-2x} =\lim_{x\to 0} [1+(-2x)]^{\frac{1}{-2x} (-2)} =e^{-2}$.

$515$.$\displaystyle \lim_{x\to \infty } \left( \dfrac{x+a}{x-a} \right)^x $.

解$\quad \displaystyle \lim_{x\to \infty } \left( \dfrac{x+a}{x-a} \right)^x =\lim_{x\to \infty } \left( 1+\dfrac{1}{\dfrac{x-a}{2a} } \right)^{\frac{x-a}{2a} \cdot 2a+a} =e^{2a}$.

$516$.$\displaystyle \lim_{x\to \infty } \left( \dfrac{a_1 x+b_1 }{a_2 x+b_2 } \right)^x (a_1 >0 ,a_2 > 0)$.

解$\quad $若$a_1 > a_2 $，则有$\dfrac{a_1 x+b_1 }{a_2 x+b_2 } \to \dfrac{a_1 }{a_2} > 1(x\to +\infty )$，可见极限为$+\infty $.若$a_1 < a_2 $，则同样可见极限为$0$.

在$a_1 =a_2 (=a)$时为$1^{\infty }$型的不定式.用$\eqref{6} $的方法就有

$$\lim_{x\to \infty } \left( \dfrac{a_1 x+b_1 }{a_2 x+b_2 } \right)^x =e^{\lim\limits_{x\to +\infty } \frac{(b_1 -b_2 )x}{ax+b_2 } } =e^{\frac{b_1 -b_2 }{a} } .$$

$517$.$\displaystyle \lim_{x\to 0} (1+x^2)^{\cot{}^2 x} $.

解$\displaystyle \lim_{x\to 0} (1+x^2)^{\cot{}^2 x} =\lim_{x\to 0} (1+x^2)^{\frac{1}{x^2} \cdot \left( \frac{x}{\sin{x} } \right)^2 \cos{}^2 x} =e$.

$518$.$\displaystyle \lim_{x\to 1} (1+\sin{\pi x} )^{\cot{\pi x} } $.

解$\displaystyle \lim_{x\to 1} (1+\sin{\pi x} )^{\cot{\pi x} } =\lim_{x\to 1} (1+\sin{\pi x} )^{\frac{1}{\sin{\pi x} } \cdot \cos{\pi x} } =e^{-1}$.

$519$.$(a)\displaystyle \lim_{x\to 0} \left( \dfrac{1+\tan{x} }{1+\sin{x} } \right)^{\frac{1}{\sin{x} } } $；$(b)\displaystyle \lim_{x\to 0} \left( \dfrac{1+\tan{x} }{1+\sin{x} } \right)^{\frac{1}{\sin{}^3 x } } $.

解$\quad (a)\displaystyle \lim_{x\to 0} \left( \dfrac{1+\tan{x} }{1+\sin{x} } \right)^{\frac{1}{\sin{x} } } =\lim_{x\to 0} \left( 1+\dfrac{1}{\dfrac{1+\sin{x} }{\tan{x} -\sin{x} } } \right)^{\frac{1+\sin{x} }{\tan{x} -\sin{x} } \cdot \frac{1-\cos{x} }{\cos{x} (1+\sin{x} )} } =e^0 =1$.

$\quad (b)\displaystyle \lim_{x\to 0} \left( \dfrac{1+\tan{x} }{1+\sin{x} } \right)^{\frac{1}{\sin{}^3 x } } =\lim_{x\to 0} \left( 1+\dfrac{1}{\dfrac{1+\sin{x} }{\tan{x} -\sin{x} } } \right)^{\frac{1+\sin{x} }{\tan{x} -\sin{x} } \cdot \frac{1-\cos{x} }{\cos{x} (1+\sin{x} ) \sin{}^2 x} } =\sqrt{e} $.

$520$.$\displaystyle \lim_{x\to a} \left( \dfrac{\sin{x} }{\sin{a} } \right)^{\frac{1}{x-a} } $.

解$\quad \displaystyle \lim_{x\to a} \left( \dfrac{\sin{x} }{\sin{a} } \right)^{\frac{1}{x-a} } =\lim_{x\to a} \left( 1+\dfrac{1}{\dfrac{\sin{a} }{\sin{x} -\sin{a} } } \right)^{\frac{\sin{a} }{\sin{x} -\sin{a} } \cdot \frac{\sin{x} -\sin{a} }{x-a} \cdot \frac{1}{\sin{a} } } =e^{\cot{a} }$，

其中，$a\neq k\pi ,k=0,\pm 1,\pm 2,\cdots $.

$521$.$\displaystyle \lim_{x\to 0} \left( \dfrac{\cos{x} }{\cos{2x} } \right)^{\frac{1}{x^2} } $.

解$\quad \displaystyle \left( \dfrac{\cos{x} }{\cos{2x} } \right)^{\frac{1}{x^2} } =\left( 1+\dfrac{1}{\dfrac{\cos{2x} }{\cos{x} -\cos{2x} } } \right)^{\frac{\cos{2x} }{\cos{x} -\cos{2x} } \cdot \frac{\cos{x} -\cos{2x} }{x^2 \cos{2x} } }$.

因为

$$\begin{align}
& \frac{\cos{x} -\cos{2x} }{x^2 } \\
= & \dfrac{\cos{x} +1-2\cos{}^2 x}{x^2} \\
= & \dfrac{1-\cos{x} }{x^2} (1+2\cos{x} ) \\
= & \dfrac{\dfrac{1}{2} x^2}{x^2} (1+2\cos{x} ) \\
\to & \dfrac{3}{2} (x\to 0),
\end{align}$$

所以，$\displaystyle \lim_{x\to 0} \left( \dfrac{\cos{x} }{\cos{2x} } \right)^{\frac{1}{x^2} } =e^{\frac{3}{2} }$.

$522$.$\displaystyle \lim_{x\to \frac{\pi }{4} } (\tan{x} )^{\tan{2x} } $.

解$\quad \displaystyle \lim_{x\to \frac{\pi }{4} } (\tan{x} )^{\tan{2x} } =\lim_{x\to \frac{\pi }{4} } (\tan{x} )^{\frac{2\tan{x} }{1-\tan{}^2 x} } =\lim_{x\to \frac{\pi }{4} } (1+\tan{x} -1)^{\frac{1}{\tan{x} -1} \frac{-2\tan{x} }{1+\tan{x}} } =e^{-1}$.

$523$.$\displaystyle \lim_{x\to \frac{\pi }{2} } (\sin{x} )^{\tan{x} } $.

解$\quad \displaystyle \lim_{x\to \frac{\pi }{2} } (\sin{x} )^{\tan{x} } =\lim_{x\to \frac{\pi }{2} } (1+\cot{}^2 x )^{-\frac{\tan{x} }{2} } =\lim_{x\to \frac{\pi }{2} } (1+\cot{}^2 x )^{\frac{1}{\cot{}^2 x} \frac{-\cot{x} }{2} } =e^0 =1$.

$524$.$\displaystyle \lim_{x\to 0} \left[ \tan{\left( \dfrac{\pi }{4} -x\right) } \right]^{\cot{x} } $.

解

$$\begin{align}
& \lim_{x\to 0} \left[ \tan{\left( \dfrac{\pi }{4} -x\right) } \right]^{\cot{x} } \\
= & \lim_{x\to 0} \left( \dfrac{1-\tan{x} }{1+\tan{x} } \right)^{\cot{x} } \\
= & \lim_{x\to 0} \left( 1+\dfrac{1}{\dfrac{1+\tan{x} }{-2\tan{x} } } \right)^{\frac{1+\tan{x} }{-2\tan{x} } \cdot \frac{-2}{1+\tan{x} } } \\
= & e^{-2} .
\end{align}$$

$525$.$\displaystyle \lim_{x\to \infty } \left( \sin{\dfrac{1 }{x} } +\cos{\dfrac{1 }{x} } \right)^{x} $.

解

$$\begin{align}
& \lim_{x\to \infty } \left( \sin{\dfrac{1 }{x} } +\cos{\dfrac{1 }{x} } \right)^{x} \\
= & \lim_{x\to \infty } \left[ 1+\left( \sin{\dfrac{1 }{x} } +\cos{\dfrac{1 }{x} } -1 \right)\right]^{\frac{1}{\sin{\frac{1 }{x} } +\cos{\frac{1 }{x} } -1 } \cdot x(\sin{\frac{1 }{x} } +\cos{\frac{1 }{x} } -1 )} .
\end{align}$$

因为

$$\begin{align}
& x(\sin{\dfrac{1 }{x} } +\cos{\dfrac{1 }{x} } -1 ) \\
= & \dfrac{\sin{\dfrac{1 }{x} } }{\dfrac{1}{x} } +\dfrac{-\dfrac{1}{2} \cdot \dfrac{1}{x^2} }{\dfrac{1}{x} } \\
\to & 1 (x\to \infty ),
\end{align}$$

所以，$\displaystyle \lim_{x\to \infty } \left( \sin{\dfrac{1 }{x} } +\cos{\dfrac{1 }{x} } \right)^{x} =e$.

$526$.$\displaystyle \lim_{x\to 0} \sqrt[x]{\cos{\sqrt{x} } } $.

解

$$\begin{align}
& \lim_{x\to 0} \sqrt[x]{\cos{\sqrt{x} } } \\
= & \lim_{x\to 0} (1+\cos{\sqrt{x} } -1)^{\frac{1}{\cos{\sqrt{x} } -1} \cdot \frac{\cos{\sqrt{x} } -1}{x} } \\
= & \lim_{x\to 0} (1+\cos{\sqrt{x} } -1)^{\frac{1}{\cos{\sqrt{x} } -1} \cdot \frac{-\frac{1}{2} x}{x} } \\
= & e^{-\frac{1}{2} } .
\end{align}$$

$527$.$\displaystyle \lim_{n\to \infty } \left( \dfrac{n+x }{n-1} \right)^{n} $.

解$\quad \displaystyle \lim_{n\to \infty } \left( \dfrac{n+x }{n-1} \right)^{n} =\lim_{n\to \infty } \left( 1+\dfrac{1}{\dfrac{n-1}{1+x} } \right)^{\frac{n-1}{1+x} \cdot (1+x)+1 } =e^{x+1}$.

$528$.$\displaystyle \lim_{n\to \infty } \cos{}^n \dfrac{x}{\sqrt{n} } $.

解

$$\begin{align}
& \lim_{n\to \infty } \cos{}^n \dfrac{x}{\sqrt{n} } \\
= & \lim_{n\to \infty } \left( 1+\cos{\dfrac{x}{\sqrt{n} } } -1\right)^n \\
= & \lim_{n\to \infty } \left( 1+\cos{\dfrac{x}{\sqrt{n} } } -1\right)^{\frac{1}{\cos{\frac{x}{\sqrt{n} } } -1} \cdot (\cos{\frac{x}{\sqrt{n} } } -1)n} \\
= & \lim_{n\to \infty } \left( 1+\cos{\dfrac{x}{\sqrt{n} } } -1\right)^{\frac{1}{\cos{\frac{x}{\sqrt{n} } } -1} \cdot (-\frac{1}{2} \frac{x^2}{n} )n} \\
= & e^{-\frac{x^2}{2} } .
\end{align}$$

$529$.$\displaystyle \lim_{x\to 0} \dfrac{\ln (1+x)}{x} $.

解$\quad \displaystyle \lim_{x\to 0} \dfrac{\ln (1+x)}{x} =\lim_{x\to 0} \ln (1+x)^{\frac{1}{x} } =\ln e=1$.

$530$.$\displaystyle \lim_{x\to +\infty } x[\ln (x+1)-\ln x] $.

解$\quad \displaystyle \lim_{x\to +\infty } x[\ln (x+1)-\ln x] =\lim_{x\to +\infty } \ln \left( 1+\dfrac{1}{x} \right)^x =\ln e=1$.

$531$.$\displaystyle \lim_{x\to a} \dfrac{\ln x-\ln a}{x-a} (a > 0) $.

解$\quad \displaystyle \lim_{x\to a} \dfrac{\ln x-\ln a}{x-a} =\lim_{x\to a} \dfrac{\ln \dfrac{x}{a} }{x-a} =\lim_{x\to a} \ln \left( 1+\dfrac{1}{\dfrac{a}{x-a} } \right)^{\frac{a}{x-a} \cdot \frac{1}{a} } =\ln e^{\frac{1}{a} } =\dfrac{1}{a} $.

$532$.$\displaystyle \lim_{x\to +\infty } [\sin{\ln (x+1)} -\sin{\ln x} ] $.

解$\quad \sin{\ln (x+1)} -\sin{\ln x} =2\cos{\dfrac{\ln (x+1)+\ln x}{2} } \sin{\dfrac{\ln (x+1)-\ln x}{2} } $.

因为

$$\ln (x+1)-\ln x=\ln \left( 1+\dfrac{1}{x} \right) \to 0(x\to +\infty ),$$

所以，$\sin{\dfrac{\ln (x+1)-\ln x}{2} } \to 0$；又因$\cos{\dfrac{\ln (x+1)+\ln x}{2} } $为有界函数，所以，$\displaystyle \lim_{x\to +\infty } [\sin{\ln (x+1)} -\sin{\ln x} ] =0$.

$533$.$\displaystyle \lim_{x\to +\infty } \dfrac{\ln (x^2-x+1)}{\ln (x^{10} +x+1)} $.

解

$$\begin{align}
& \lim_{x\to +\infty } \dfrac{\ln (x^2-x+1)}{\ln (x^{10} +x+1)} \\
= & \lim_{x\to +\infty } \dfrac{2\ln x+\ln (1-\dfrac{1}{x} +\dfrac{1}{x^2} )}{10\ln x+\ln (1 +\dfrac{1}{x^9} +\dfrac{1}{x^{10}} )} \\
= & \lim_{x\to +\infty } \dfrac{2+\dfrac{1}{\ln x} \cdot \ln (1-\dfrac{1}{x} +\dfrac{1}{x^2} )}{10+\dfrac{1}{\ln x} \cdot \ln (1 +\dfrac{1}{x^9} +\dfrac{1}{x^{10}} )} \\
= & \dfrac{1}{5} .
\end{align}$$

$534$.$\displaystyle \lim_{x\to \infty } \left( \lg \dfrac{100+x^2}{1+100x^2} \right) $.

解$\quad \displaystyle \lim_{x\to \infty } \left( \lg \dfrac{100+x^2}{1+100x^2} \right) =\lg \dfrac{1}{100} =-2$.

$535$.$\displaystyle \lim_{x\to +\infty } \dfrac{\ln (2+e^{3x} )}{\ln (3+e^{2x})} $.

解

$$\begin{align}
& \lim_{x\to +\infty } \dfrac{\ln (2+e^{3x} )}{\ln (3+e^{2x})} \\
= & \lim_{x\to +\infty } \dfrac{3x+\ln (2e^{-3x}+1 )}{2x+\ln (3e^{-2x} +1)} \\
= & \lim_{x\to +\infty } \dfrac{3+\dfrac{1}{x} \ln (2e^{-3x}+1 )}{2+\dfrac{1}{x} \ln (3e^{-2x} +1)} \\
= & \dfrac{3}{2} .
\end{align}$$

$536$.$\displaystyle \lim_{x\to +\infty } \dfrac{\ln (1+\sqrt{x} +\sqrt[3]{x} )}{\ln (1+\sqrt[3]{x} +\sqrt[4]{x} )} $.

解

$$\begin{align}
& \lim_{x\to +\infty } \dfrac{\ln (1+\sqrt{x} +\sqrt[3]{x} )}{\ln (1+\sqrt[3]{x} +\sqrt[4]{x} )} \\
= & \lim_{x\to +\infty } \dfrac{\dfrac{1}{2} \ln x+\ln (x^{-\frac{1}{2} }+1+x^{-\frac{1}{6} })}{\dfrac{1}{3} \ln x+\ln (x^{-\frac{1}{3} }+1+x^{-\frac{1}{12} })} \\
= & \lim_{x\to +\infty } \dfrac{\dfrac{1}{2} +\dfrac{1}{\ln x} \cdot \ln (x^{-\frac{1}{2} }+1+x^{-\frac{1}{6} })}{\dfrac{1}{3} +\dfrac{1}{\ln x} \cdot \ln (x^{-\frac{1}{3} }+1+x^{-\frac{1}{12} })} \\
= & \dfrac{3}{2} .
\end{align}$$

$537$.$\displaystyle \lim_{h\to 0} \dfrac{\log (x+h)+\log (x-h)-2\log x}{h^2} (x > 0)$.

解

$$\begin{align}
& \lim_{h\to 0} \dfrac{\log (x+h)+\log (x-h)-2\log x}{h^2} \\
= & \lim_{h\to 0} \dfrac{\log (x^2-h^2)-\log x^2}{h^2} \\
= & \lim_{h\to 0} \left[ -\dfrac{1}{x^2} \log \left( 1-\dfrac{h^2}{x^2} \right)^{-\frac{x^2}{h^2} } \right] \\
= & -\dfrac{1}{x^2} \log e.
\end{align}$$

$538$.$\displaystyle \lim_{x\to 0} \dfrac{\ln \tan{\left( \dfrac{\pi }{4} +ax\right) } }{\sin{bx} } $.

解

$$\begin{align}
& \lim_{x\to 0} \dfrac{\ln \tan{\left( \dfrac{\pi }{4} +ax\right) } }{\sin{bx} } \\
= & \lim_{x\to 0} \ln \left[ 1+\left( \tan{\left( \dfrac{\pi }{4} +ax\right) } -1\right) \right]^{\frac{1}{\sin{bx} } } \\
= & \lim_{x\to 0} \ln \left[ 1+\dfrac{\sin{\left( \dfrac{\pi }{4} +ax\right) } -\cos{\left( \dfrac{\pi }{4} +ax\right) } }{\cos{\left( \dfrac{\pi }{4} +ax\right) } } \right]^{\frac{1}{\sin{bx} } } \\
= & \lim_{x\to 0} \ln \left[ 1+\dfrac{\sqrt{2} \sin{ax} }{\cos{\left( \dfrac{\pi }{4} +ax\right) } } \right]^{\frac{\cos{\left( \frac{\pi }{4} +ax\right) } }{\sqrt{2} \sin{ax} } \cdot \frac{\sqrt{2} }{\cos{\left( \frac{\pi }{4} +ax\right) } } \frac{\sin{ax} }{ax} \cdot \frac{bx}{\sin{bx} } \cdot \frac{a}{b} } \\
= & \ln e^{\frac{2a}{b} } \\
= & \dfrac{2a}{b} .
\end{align}$$

$539$.$\displaystyle \lim_{x\to 0} \dfrac{\ln \cos{ax} }{\ln \cos{bx} } $.

解

$$\begin{align}
& \lim_{x\to 0} \dfrac{\ln \cos{ax} }{\ln \cos{bx} } \\
= & \lim_{x\to 0} \left( \dfrac{\ln \cos{ax} }{\cos{ax} -1} \cdot \dfrac{\cos{bx} -1}{\ln \cos{bx} } \cdot \dfrac{\cos{ax} -1 }{\cos{bx} -1} \right) \\
= & \lim_{x\to 0} \dfrac{2\sin{}^2 \dfrac{ax}{2} }{2\sin{}^2 \dfrac{bx}{2} } \\
= & \dfrac{a^2}{b^2} .
\end{align}$$

$540$.$(a)\displaystyle \lim_{x\to 0} \left( \ln \dfrac{nx+\sqrt{1-n^2 x^2} }{x+\sqrt{1-x^2} } \right) $；$(b)\displaystyle \lim_{x\to 0} \dfrac{\ln (nx+\sqrt{1-n^2 x^2} )}{\ln (x+\sqrt{1-x^2} )} $.

解$\quad (a)\displaystyle \lim_{x\to 0} \left( \ln \dfrac{nx+\sqrt{1-n^2 x^2} }{x+\sqrt{1-x^2} } \right) =\ln 1=0$.

下面是综合利用等价量代换法与其他方法的例子.

$(b)$先看出是$\dfrac{0}{0} $型的不定式.分母可改写如下：

$$\ln (x+\sqrt{1-x^2} ) =\dfrac{1}{2} \ln (x+\sqrt{1-x^2} )^2 =\dfrac{1}{2} \ln (1+2x\sqrt{1-x^2} ).$$

于是即可用$\eqref{3} $的$\ln (1+x)\sim x(x\to 0)$时分母等价于$x\sqrt{1-x^2} $，而后者又等价于$x$.

又可看出只要将分母中的$x$换为$nx$就得到分子，从而当$x\to 0$时分子等价于$nx$.因此极限为$n$.

$541$.$\displaystyle \lim_{x\to 0} \dfrac{a^x -1}{x} (a > 0)$.

解$\quad $设$a^x -1=y$，则

$$\lim_{x\to 0} \dfrac{a^x -1}{x} =\lim_{y\to 0} \dfrac{y}{\log_a (1+y)} =\lim_{y\to 0} \dfrac{1}{\log_a (1+y)^{\frac{1}{y} }} =\dfrac{1}{\log_a e} =\ln a.$$

$542$.$\displaystyle \lim_{x\to a} \dfrac{a^x -x^a}{x-a} (a > 0)$.

解

$$\begin{align}
& \dfrac{a^x -x^a}{x-a} \\
= & \dfrac{a^a \left[ a^{x-a} -\left( \dfrac{x}{a} \right)^a \right] }{x-a} \\
= & a^a \cdot \dfrac{a^{x-a} -1}{x-a} -a^a \dfrac{\left( \dfrac{x}{a} \right)^a -1}{x-a} \\
= & a^a \cdot \dfrac{a^{x-a} -1}{x-a} -a^a \dfrac{e^{a\ln \frac{x}{a} } -1}{a\ln \dfrac{x}{a} } \cdot \dfrac{a\ln \left( 1+\dfrac{x-a}{a} \right) }{x-a} ,
\end{align}$$

当$x\to a$时，等式第一项趋向$a^a \ln a$，而第二项趋向$a^a \cdot 1\cdot 1=a^a$，所以，

$$ \lim_{x\to a} \dfrac{a^x -x^a}{x-a} =a^a \ln a-a^a =a^a \ln \dfrac{a}{e} .$$

$543$.$\displaystyle \lim_{x\to a} \dfrac{x^x -a^a}{x-a} (a > 0)$

解$\quad $改写分子的两项为$e$的幂，然后利用$\eqref{3} $，$\eqref{4}$得到

$$\begin{align}
& \lim_{x\to a} \dfrac{e^{x\ln x} -e^{a\ln a}}{x-a} \\
= & a^a \cdot \lim_{x\to a} \left( \dfrac{e^{x\ln x-a\ln a} -1}{x\ln x-a\ln a} \cdot \dfrac{x\ln x-a\ln a}{x-a} \right) \\
= & a^a \cdot \lim_{x\to a} \dfrac{x\ln x-a\ln x+a\ln x-a\ln a}{x-a} \\
= & a^a \left( \lim_{x\to a} \ln x+\lim_{x\to a} \dfrac{\ln \left( 1+\dfrac{x-a}{a} \right) }{\dfrac{x-a}{a} } \right) \\
= & a^a (\ln a+1).
\end{align}$$

$544$.$\displaystyle \lim_{x\to 0} (x+e^x)^{\frac{1}{x} }$.

解$\quad \displaystyle \lim_{x\to 0} (x+e^x)^{\frac{1}{x} } =\lim_{x\to 0} e\left( 1+\dfrac{x}{e^x} \right)^{\frac{e^x}{x} \cdot e^{-x}} =e\cdot e=e^2$.

$545$.$(a)\displaystyle \lim_{x\to 0} \left( \dfrac{1+x\cdot 2^x}{1+x\cdot 3^x} \right)^{\frac{1}{x^2} } $；$(b)\displaystyle \lim_{x\to 0} \left( \dfrac{1+\sin{x} \cos{\alpha x} }{1+\sin{x} \cos{\beta x} } \right)^{\cot{}^3 x} $；

$(c)\displaystyle \lim_{x\to 1} \dfrac{\sin{(\pi x^{\alpha } )}}{\sin{(\pi x^{\beta })} } $；$(d)\displaystyle \lim_{x\to 1} \dfrac{\sin{}^2 (\pi \cdot 2^x )}{\ln \cos{(\pi \cdot 2^x)} } $.

解$\quad (a)\displaystyle \lim_{x\to 0} \left( \dfrac{1+x\cdot 2^x}{1+x\cdot 3^x} \right)^{\frac{1}{x^2} } =\left( 1+\dfrac{1}{\dfrac{1+x\cdot 3^x}{x(2^x -3^x)} } \right)^{\frac{1+x\cdot 3^x}{x(2^x -3^x)} \cdot \frac{2^x-3^x}{x(1+x\cdot 3^x)} } $.

因为

$$\begin{align}
& \dfrac{2^x-3^x}{x(1+x\cdot 3^x)} \\
= & \dfrac{1}{1+x\cdot 3^x} \cdot \left( \dfrac{2^x-1}{x} -\dfrac{3^x -1}{x} \right) \\
\to & \ln 2-\ln 3 \\
= & \ln \dfrac{2}{3} (x\to 0),
\end{align}$$

所以，$\displaystyle \lim_{x\to 0} \left( \dfrac{1+x\cdot 2^x}{1+x\cdot 3^x} \right)^{\frac{1}{x^2} } =e^{\ln \frac{2}{3} } =\dfrac{2}{3} $.

$(b)$这是$1^{\infty }$型不定式.将括号内写成$1+o(1)$后用$\eqref{6}$的方法，只要计算下列极限：

$$\begin{align}
& \lim_{x\to 0} \left( \dfrac{\sin{x} (\cos{\alpha x} -\cos{\beta x} )}{1+\sin{x} \cos{\beta x} } \cdot \dfrac{\cos{}^3 x}{\sin{}^3 x} \right) \\
= & \lim_{x\to 0} \dfrac{\cos{\alpha x} -1+1-\cos{\beta x} }{x^2} \\
= & \dfrac{1}{2} (-\alpha^2 +\beta^2),
\end{align}$$

就可知答案为$e^{\frac{\beta^2 -\alpha^2 }{2}} $.

$(c)$这是$\dfrac{0}{0}$型不定式.令$t=x-1$，并改写分子分母，就可以如下求解（其中两次利用了$\sin{x} \sim x(x\to 0)$和$\eqref{5}$）:

$$\begin{align}
& \lim_{t\to 0} \dfrac{\sin{[\pi ((t+1)^{\alpha } -1)]} }{\sin{[\pi ((t+1)^{\beta } -1)]} } \\
= & \lim_{t\to 0} \dfrac{\pi ((t+1)^{\alpha } -1) }{\pi ((t+1)^{\beta } -1)} \\
= & \lim_{t\to 0} \left( \dfrac{(t+1)^{\alpha } -1}{t} \cdot \dfrac{t}{(t+1)^{\beta } -1} \right) \\
= & \dfrac{\alpha }{\beta } .
\end{align}$$

$(d)$这是$\dfrac{0}{0}$型的不定式.令$t=x-1$，并将两个三角函数的自变量改写为$2\pi \cdot (2t-1)$，然后利用$x\to 0$时的等价关系$\sin{x} \sim x$，$1-\cos{x} \sim \dfrac{1}{2} x^2 $和$\ln (1+x)\sim x$，即可计算得到：

$$\lim_{t\to 0} \dfrac{\sin{}^2 (2\pi \cdot (2^t -1))}{\cos{(2\pi \cdot (2^t -1))-1}} =-2.$$

$546$.$\displaystyle \lim_{n\to \infty } \tan{}^n \left( \dfrac{\pi }{4} +\dfrac{1}{n} \right) $.

解

$$\begin{align}
& \lim_{n\to \infty } \tan{}^n \left( \dfrac{\pi }{4} +\dfrac{1}{n} \right) \\
= & \lim_{n\to \infty } \left( \dfrac{1+\tan{\dfrac{1}{n} } }{1-\tan{\dfrac{1}{n} } } \right)^n \\
= & \lim_{n\to \infty } \left( 1+\dfrac{1}{\dfrac{1-\tan{\dfrac{1}{n} } }{2\tan{\dfrac{1}{n} } } } \right)^{\frac{1-\tan{\frac{1}{n} } }{2\tan{\frac{1}{n} } } \cdot \frac{2\tan{\frac{1}{n} } }{\frac{1}{n} } \cdot \frac{1}{1-\tan{\frac{1}{n} } } } \\
= & e^2.
\end{align}$$

$547$.$\displaystyle \lim_{x\to 0} \dfrac{e^{\alpha x} -e^{\beta x} }{\sin{\alpha x} -\sin{\beta x} } $.

解

$$\begin{align}
& \lim_{x\to 0} \dfrac{e^{\alpha x} -e^{\beta x} }{\sin{\alpha x} -\sin{\beta x} } \\
= & \lim_{x\to 0} \dfrac{e^{\beta x} [e^{(\alpha -\beta ) x} -1] }{2\cos{\dfrac{\alpha +\beta }{2} x} \sin{\dfrac{\alpha -\beta }{2} x} } \\
= & \lim_{x\to 0} \dfrac{e^{(\alpha -\beta ) x} -1}{(\alpha -\beta )x} \cdot \dfrac{\dfrac{\alpha -\beta }{2} x}{\sin{\dfrac{\alpha -\beta }{2} x}} \cdot \dfrac{e^{\beta x} }{\cos{\dfrac{\alpha +\beta }{2} x} }\\
= & \ln e \\
= & 1.
\end{align}$$

$548$.$\displaystyle \lim_{x\to a} \dfrac{x^{\alpha } -a^{\alpha }}{x^{\beta }-a^{\beta } } (a > 0)$.

解

$$\begin{align}
& \dfrac{x^{\alpha } -a^{\alpha }}{x^{\beta }-a^{\beta } } \\
= & a^{\alpha -\beta } \cdot \dfrac{\left( \dfrac{x}{a} \right)^{\alpha } -1}{\left( \dfrac{x}{a} \right)^{\beta } -1}\\
= & a^{\alpha -\beta } \cdot \dfrac{e^{\alpha \ln \frac{x}{a} } -1}{\alpha \ln \dfrac{x}{a}} \cdot \dfrac{\beta \ln \dfrac{x}{a} }{e^{\beta \ln \frac{x}{a} } -1} \cdot \dfrac{\alpha }{\beta } .
\end{align}$$

当$x\to a $时，$\ln \dfrac{x}{a} \to 0$，于是上式趋向$\dfrac{\alpha }{\beta } a^{\alpha -\beta } $，即

$$\lim_{x\to a} \dfrac{x^{\alpha } -a^{\alpha }}{x^{\beta }-a^{\beta } } =\dfrac{\alpha }{\beta } a^{\alpha -\beta } (\beta \neq 0).$$

$549$.$\displaystyle \lim_{x\to b} \dfrac{a^x -a^b}{x-b} (a > 0)$.

解$\quad \displaystyle \lim_{x\to b} \dfrac{a^x -a^b}{x-b} =\lim_{x\to b} \left( a^b \cdot \dfrac{a^{x-b} -1}{x-b} \right) =a^b \ln a$.

$550$.$\displaystyle \lim_{h\to 0} \dfrac{a^{x+h} +a^{x-h}-2a^x}{h^2} (a > 0)$.

解

$$\begin{align}
& \lim_{h\to 0} \dfrac{a^{x+h} +a^{x-h}-2a^x}{h^2} \\
= & \lim_{h\to 0} \left( a^x \cdot \dfrac{a^h +a^{-h}-2}{h^2} \right) \\
= & \lim_{h\to 0} \dfrac{a^x }{a^h} \left( \dfrac{a^h -1}{h} \right)^2 \\
= & a^x \ln^2 a.
\end{align}$$

$551$.$\displaystyle \lim_{x\to \infty } \dfrac{(x+a)^{x+a} (x+b)^{x+b} }{(x+a+b)^{2x+a+b}} $.

解

$$\begin{align}
& \lim_{x\to \infty } \dfrac{(x+a)^{x+a} (x+b)^{x+b} }{(x+a+b)^{2x+a+b}} \\
= & \lim_{x\to \infty } \dfrac{\left(1+\dfrac{a}{x} \right)^{x+a} \left(1+\dfrac{b}{x} \right)^{x+b} }{\left(1+\dfrac{a+b}{x} \right)^{2x+a+b}} \\
= & \lim_{x\to \infty } \dfrac{\left(1+\dfrac{a}{x} \right)^{\frac{x}{a} a+a} \left(1+\dfrac{b}{x} \right)^{\frac{x}{b} b +b} }{\left(1+\dfrac{a+b}{x} \right)^{\frac{x}{a+b} [2(a+b)]+a+b}} \\
= & \dfrac{e^a \cdot e^b}{e^{2(a+b)}} \\
= & e^{-(a+b)} .
\end{align}$$

$552$.$\displaystyle \lim_{n\to \infty } n(\sqrt[n]{x} -1) (x > 0)$.

解$\quad \displaystyle \lim_{n\to \infty } n(\sqrt[n]{x} -1) =\lim_{n\to \infty } \dfrac{x^{\frac{1}{n} } -1}{\dfrac{1}{n} } =\ln x$.

$553$.$\displaystyle \lim_{n\to \infty } n^2(\sqrt[n]{x} -\sqrt[n+1]{x} ) (x > 0)$.

解

$$\begin{align}
& \lim_{n\to \infty } n^2(\sqrt[n]{x} -\sqrt[n+1]{x} ) \\
= & \lim_{n\to \infty } \dfrac{x^{\frac{1}{n} } -x^{\frac{1}{n+1} }}{\dfrac{1}{n^2} } \\
= & \lim_{n\to \infty } \dfrac{x^{\frac{1}{n+1} } [ x^{\frac{1}{n(n+1)} } -1]}{\dfrac{1}{n(n+1)} +\left( \dfrac{1}{n^2} -\dfrac{1}{n^2+n} \right) } \\
= & \lim_{n\to \infty } \left[ \dfrac{x^{\frac{1}{n(n+1)} } -1}{\dfrac{1}{n(n+1)}} \cdot \dfrac{x^{\frac{1}{n+1} }\cdot \dfrac{1}{n(n+1)} }{\dfrac{1}{n(n+1)} +\left( \dfrac{1}{n^2} -\dfrac{1}{n^2+n} \right) } \right] \\
= & \ln x.
\end{align}$$

$554$.$\displaystyle \lim_{n\to \infty } \left( \dfrac{a-1+\sqrt[n]{b} }{a} \right)^n (a > 0,b > 0) $.

解

$$\begin{align}
& \lim_{n\to \infty } \left( \dfrac{a-1+\sqrt[n]{b} }{a} \right)^n \\
= & \lim_{n\to \infty } \left( 1+\dfrac{1}{\dfrac{a}{b^{\frac{1}{n} } -1} } \right)^{\frac{a}{b^{\frac{1}{n} } -1} \cdot \frac{b^{\frac{1}{n} } -1 }{\frac{1}{n} } \cdot \frac{1}{a}} \\
= & e^{\frac{1}{a} \ln b} \\
= & \sqrt[a]{b} .
\end{align}$$

$555$.$\displaystyle \lim_{n\to \infty } \left( \dfrac{\sqrt[n]{a} +\sqrt[n]{b} }{2} \right)^n (a > 0,b > 0) $.

解

$$\begin{align}
& \lim_{n\to \infty } \left( \dfrac{\sqrt[n]{a} +\sqrt[n]{b} }{2} \right)^n \\
= & \lim_{n\to \infty } \left( 1+\dfrac{\sqrt[n]{a} +\sqrt[n]{b} }{2} -1\right)^{\left( \frac{1}{\frac{\sqrt[n]{a} +\sqrt[n]{b} }{2} -1} \right) \left( \frac{\sqrt[n]{a} +\sqrt[n]{b} }{2} -1\right) n} \\
= & e^{\frac{1}{2} (\ln a+\ln b)} \\
= & \sqrt{ab} .
\end{align}$$

$556$.$\displaystyle \lim_{x\to 0 } \left( \dfrac{a^x +b^x +c^x}{3} \right)^{\frac{1}{x} } (a > 0,b > 0,c > 0) $.

解

$$\begin{align}
& \lim_{x\to 0 } \left( \dfrac{a^x +b^x +c^x}{3} \right)^{\frac{1}{x} } \\
= & \lim_{x\to 0} \left( 1+\dfrac{a^x +b^x +c^x}{3} -1\right)^{\left( \frac{1}{\frac{a^x +b^x +c^x}{3} -1} \right) \left( \frac{a^x -1+b^x -1+c^x-1}{3x} \right) } \\
= & \sqrt[3]{abc} .
\end{align}$$

$557$.$\displaystyle \lim_{x\to 0 } \left( \dfrac{a^{x+1} +b^{x+1} +c^{x+1}}{a+b+c} \right)^{\frac{1}{x} } (a > 0,b > 0,c > 0) $.

解$\quad $由于

$$\begin{align}
& \lim_{x\to 0} \dfrac{a^{x+1} +b^{x+1} +c^{x+1}-a-b-c}{x(a+b+c)} \\
= & \dfrac{1}{a+b+c} \lim_{x\to 0} \left( a\cdot \dfrac{a^x -1}{x} +b\cdot \dfrac{b^x-1}{x} +c\cdot \dfrac{c^x -1}{x} \right) \\
= & \ln (a^a b^b c^c)^{\frac{1}{a+b+c} } ,
\end{align}$$

因而，

$$\begin{align}
& \lim_{n\to \infty } \left( \dfrac{a^{x+1} +b^{x+1} +c^{x+1}}{a+b+c} \right)^{\frac{1}{x} } \\
= & \lim_{x\to 0} \left( 1+\dfrac{a^{x+1} +b^{x+1} +c^{x+1}}{a+b+c} -1\right)^{\left( \frac{1}{\frac{a^{x+1} +b^{x+1} +c^{x+1}}{a+b+c} -1} \right) \cdot \dfrac{1}{x} \left( \frac{a^{x+1} +b^{x+1} +c^{x+1}}{a+b+c} -1 \right) } \\
= & (a^a b^b c^c )^{\frac{1}{a+b+c} } .
\end{align}$$

$558$.$\displaystyle \lim_{x\to 0} \left( \dfrac{a^{x^2} +b^{x^2} }{a^x+b^x} \right)^{\frac{1}{x} } (a > 0,b > 0) $.

解

$$\begin{align}
& \lim_{x\to 0} \left( \dfrac{a^{x^2} +b^{x^2} }{a^x+b^x} \right)^{\frac{1}{x} } \\
= & \lim_{x\to 0} \left( 1+\dfrac{1}{\dfrac{a^x+b^x}{a^{x^2}+b^{x^2} -a^x-b^x} } \right)^{\frac{a^x+b^x}{a^{x^2}+b^{x^2} -a^x-b^x} \cdot \left[ x\left(\frac{a^{x^2} -1}{x^2} +\frac{b^{x^2} -1}{x^2} \right)-\frac{a^x-1}{x} -\frac{b^x-1}{x} \right] \cdot \frac{1}{a^x+b^x} } \\
= & e^{-\frac{1}{2} (\ln a +\ln b)} \\
= & \dfrac{1}{\sqrt{ab} } .
\end{align}$$

$559$.$\displaystyle \lim_{x\to 0 } \dfrac{a^{x^2} -b^{x^2} }{(a^x -b^x )^2} (a > 0,b > 0)$.

解

$$\begin{align}
& \lim_{x\to 0 } \dfrac{a^{x^2} -b^{x^2} }{(a^x -b^x )^2} \\
= & \lim_{x\to 0} \left[ \left( \dfrac{a^{x^2} -1}{x^2} -\dfrac{b^{x^2} -1}{x^2} \right) \cdot \dfrac{1}{\left( \dfrac{a^x-1}{x} -\dfrac{b^x-1}{x} \right)^2} \right] \\
= & (\ln a-\ln b)\cdot \dfrac{1}{(\ln a-\ln b)^2} \\
= & \dfrac{1}{\ln a-\ln b } \\
= & \left( \ln \dfrac{a}{b} \right)^{-1} .
\end{align}$$

$560$.$\displaystyle \lim_{x\to a } \dfrac{a^{a^x} -a^{x^a} }{a^x -x^a } (a > 0)$.

解$\quad \displaystyle \lim_{x\to a } \dfrac{a^{a^x} -a^{x^a} }{a^x -x^a } =\lim_{x\to a} \left( a^{x^a} \cdot \dfrac{a^{a^x -x^a} -1}{a^x-x^a} \right) =a^{a^a} \ln a$.

$561$.$(a)\displaystyle \lim_{x\to -\infty } \dfrac{\ln (1+3^x)}{\ln (1+2^x)} $；$(b)\displaystyle \lim_{x\to +\infty } \dfrac{\ln (1+3^x)}{\ln (1+2^x)} $.

解$\quad (1)$

$$\begin{align}
& \lim_{x\to -\infty } \dfrac{\ln (1+3^x)}{\ln (1+2^x)} \\
= & \lim_{x\to -\infty } \left[ \dfrac{\ln (1+3^x)}{3^x} \cdot \dfrac{2^x}{\ln (1+2^x)} \cdot \left( \dfrac{2}{ 3} \right)^{-x} \right] \\
= & 1\cdot 1\cdot 0 \\
= & 0 .
\end{align}$$

$(2)$

$$\begin{align}
& \lim_{x\to +\infty } \dfrac{\ln (1+3^x)}{\ln (1+2^x)} \\
= & \lim_{x\to +\infty } \dfrac{x\ln 3+\ln (1+3^{-x})}{x\ln 2+\ln (1+2^{-x})} \\
= & \lim_{x\to +\infty } \dfrac{\ln 3+\dfrac{1}{x} \cdot \ln (1+3^{-x})}{\ln 2+\dfrac{1}{x} \cdot \ln (1+2^{-x})} \\
= & \dfrac{\ln 3}{\ln 2} .
\end{align}$$

$562$.$\displaystyle \lim_{x\to +\infty } \ln (1+2^x) \ln \left( 1+\dfrac{3}{x} \right) $.

解

$$\begin{align}
& \lim_{x\to +\infty } \ln (1+2^x) \ln \left( 1+\dfrac{3}{x} \right) \\
= & \lim_{x\to +\infty } \left[ \dfrac{\ln \left( 1+\dfrac{3}{x} \right) }{\dfrac{3}{x} } \cdot \dfrac{x\ln 2+\ln (2^{-x} +1)}{\dfrac{x}{3} } \right] \\
= & 3\ln 2 \\
= & \ln 8 .
\end{align}$$

$563$.$\displaystyle \lim_{x\to 1} (1-x)\log_x 2$.

解

$$\begin{align}
& \lim_{x\to 1} (1-x)\log_x 2 \\
= & \lim_{x\to 1} \dfrac{1-x}{\ln x} \cdot \ln 2\\
= & -\ln 2\cdot \lim_{x\to 1} \dfrac{x-1}{\ln [1+(x-1)]} \\
= & -\ln 2.
\end{align}$$

$564$.证明：

$$\lim_{x\to +\infty } \dfrac{x^n}{a^x} =0(a > 1,n > 0).$$

证$\quad $当$x\geqslant 1$时，存在唯一的正整数$k$，使

$$k\leqslant x < k+1.$$

于是当$n > 0$时，我们有

$$\dfrac{x^n}{a^x} < \dfrac{(k+1)^n}{a^k} $$

及

$$\dfrac{x^n}{a^x} > \dfrac{k^n}{a^{k+1}} =\dfrac{k^n}{a^k} \cdot \dfrac{1}{a} .$$

因为当$x\to +\infty $时，$k \to +\infty $，所以有

$$\lim_{x\to +\infty } \dfrac{(k+1)^n}{a^k} =\lim_{x\to +\infty } \dfrac{(k+1)^n}{a^{k+1}} \cdot a=0\cdot a=0$$

及

$$\lim_{x\to +\infty } \dfrac{k^n}{a^{k+1}} =\lim_{x\to +\infty } \dfrac{k^n}{a^k} \cdot \dfrac{1}{a} =0\cdot \dfrac{1}{a} =0.$$

于是，$\displaystyle \lim_{x\to +\infty } \dfrac{x^n}{a^x} =0$.

$565$.证明：

$$\lim_{x\to +\infty } \dfrac{\log_a x}{x^{\varepsilon } } =0 ,(a > 0,\varepsilon > 0).$$

证$\quad $设$\log_a x=y$，则$x=a^y $，且当$x\to +\infty $时，$y\to +\infty $.于是，

$$\lim_{x\to +\infty } \dfrac{\log_a x}{x^{\varepsilon } } =\lim_{y\to +\infty } \dfrac{y}{(a^y)^{\varepsilon }} =\lim_{y\to +\infty } \left( \dfrac{y^{\frac{1}{\varepsilon } }}{a^y} \right)^{\varepsilon } =0,$$

即

$$\lim_{x\to +\infty } \dfrac{\log_a x}{x^{\varepsilon } } =0 .$$

求下列极限：

$566$.$(a)\displaystyle \lim_{x\to 0} \dfrac{\ln (x^2+e^x)}{\ln (x^4 +e^{2x})} $；$(b)\displaystyle \lim_{x\to +\infty } \dfrac{\ln (x^2+e^x)}{\ln (x^4 +e^{2x})} $.

解$\quad (a)$

$$\begin{align}
& \lim_{x\to 0} \dfrac{\ln (x^2+e^x)}{\ln (x^4 +e^{2x})} \\
= & \lim_{x\to 0} \dfrac{x+\ln (1+x^2e^{-x})}{2x+\ln (1+x^4 e^{-2x})}\\
= & \lim_{x\to 0} \dfrac{1+\dfrac{\ln (1+x^2e^{-x})}{x^2e^{-x}} \cdot xe^{-x}}{2+\dfrac{\ln (1+x^4 e^{-2x})}{x^4e^{-2x}} \cdot x^3e^{-2x}} \\
= & \dfrac{1}{2} .
\end{align}$$

$(b)\displaystyle \lim_{x\to +\infty } \dfrac{\ln (x^2+e^x)}{\ln (x^4 +e^{2x})} =\lim_{x\to +\infty } \dfrac{1+\dfrac{\ln (1+x^2e^{-x})}{x} }{2+\dfrac{\ln (1+x^4 e^{-2x})}{x}} =\dfrac{1}{2} $，

其中利用了结果$\displaystyle \lim_{x\to +\infty } x^n a^{-x} =0(n > 0 ,a > 1)$，因而，

$$x^2e^{-x} \to 0,x^4e^{-2x} \to 0(x\to +\infty ).$$

$567$.$\displaystyle \lim_{x\to 0} \dfrac{\ln (1+xe^x)}{\ln (x+\sqrt{1+x^2} )} $.

解

$$\begin{align}
& \lim_{x\to 0} \dfrac{\ln (1+xe^x)}{\ln (x+\sqrt{1+x^2} )} \\
= & \lim_{x\to 0} \dfrac{\dfrac{\ln (1+xe^x)}{xe^x} \cdot xe^x}{\dfrac{1}{2} \ln (1+x^2)+\dfrac{\ln \left( 1+\dfrac{x}{\sqrt{1+x^2} } \right)}{\dfrac{x}{\sqrt{1+x^2}}}\cdot \dfrac{x}{\sqrt{1+x^2} } } \\
= & \lim_{x\to 0} \dfrac{xe^x}{\dfrac{x}{\sqrt{1+x^2} } } \\
= & \lim_{x\to 0} e^x \sqrt{1+x^2} \\
= & 1.
\end{align}$$

$568$.$\displaystyle \lim_{x\to +\infty } [(x+2)\ln (x+2)-2(x+1)\ln (x+1)+x\ln x]$.

解

$$\begin{align}
& \lim_{x\to +\infty } [(x+2)\ln (x+2)-2(x+1)\ln (x+1)+x\ln x] \\
= & \lim_{x\to +\infty } \ln \dfrac{(x+2)^{x+2} \cdot x^x}{(x+1)^{2x+2}} \\
= & \lim_{x\to +\infty } \ln \dfrac{(1+\dfrac{2}{x} )^{\frac{x}{2} \cdot 2+2} }{(1+\dfrac{1}{x})^{2x+2}} \\
= & \lim_{x\to +\infty } \ln \dfrac{e^2}{e^2} \\
= & 0.
\end{align}$$

$569$.$\displaystyle \lim_{x\to +0} \left[ \ln (x\ln a)\cdot \ln \left( \dfrac{\ln ax}{\ln \dfrac{x}{a} } \right) \right] (a > 1)$.

解

$$\begin{align}
& \lim_{x\to +0} \left[ \ln (x\ln a)\cdot \ln \left( \dfrac{\ln ax}{\ln \dfrac{x}{a} } \right) \right] \\
= & \lim_{x\to +0} \ln \left( \dfrac{\ln a +\ln x}{\ln x-\ln a} \right)^{\ln x+\ln (\ln a)} \\
= & \lim_{x\to +0} \ln \left( 1+\dfrac{2\ln a}{\ln x-\ln a} \right)^{\ln x+\ln (\ln a)} \\
= & \lim_{x\to +0} \ln \left( 1+\dfrac{2\ln a}{\ln x-\ln a} \right)^{\frac{\ln x-\ln a}{2\ln a} \cdot 2\ln a\cdot \frac{\ln x+\ln (\ln a)}{\ln x-\ln a} } \\
= & \ln e^{\ln a^2} \\
= & \ln a^2.
\end{align}$$

$570$.$\displaystyle \lim_{x\to +\infty } \left( \ln \dfrac{x+\sqrt{x^2+1} }{x+\sqrt{x^2-1} } \cdot {\ln }^{-2} \dfrac{x+1}{x-1} \right) $.

解

$$\begin{align}
& \lim_{x\to +\infty } \left( \ln \dfrac{x+\sqrt{x^2+1} }{x+\sqrt{x^2-1} } \cdot {\ln }^{-2} \dfrac{x+1}{x-1} \right) \\
= & \lim_{x\to +\infty } \dfrac{\ln \left( 1+\dfrac{\sqrt{x^2+1} -\sqrt{x^2-1} }{x+\sqrt{x^2-1} } \right) }{ {\ln }^2 \left( 1+\dfrac{2}{x-1} \right) } \\
= & \lim_{x\to +\infty } \dfrac{\left\lbrace \ln \left[ 1+\dfrac{2}{(x+\sqrt{x^2-1} ) (\sqrt{x^2+1} +\sqrt{x^2-1} ) } \right] ^{\frac{(x+\sqrt{x^2-1} ) }{\sqrt{2} } } \right. }{ {\ln }^2 \left[ \left( 1+\dfrac{2}{x-1} \right) ^{\frac{x-1}{2} } \right] } \\
& \dfrac{\left. {\dfrac{ }{ } }^{\cdot \frac{(\sqrt{x^2+1} +\sqrt{x^2-1} )}{\sqrt{2} } } \right\rbrace \cdot \dfrac{2}{(x+\sqrt{x^2-1} )(\sqrt{x^2+1} +\sqrt{x^2-1} )} }{ \left( \dfrac{2}{x-1} \right)^2 } \\
= & \lim_{x\to +\infty } \dfrac{(x-1)^2}{2(x+\sqrt{x^2-1} )(\sqrt{x^2+1} +\sqrt{x^2-1} )} \\
= & \lim_{x\to +\infty } \dfrac{\left( 1-\dfrac{1}{x} \right)^2 }{2\left( 1+\sqrt{1-\dfrac{1}{x^2} } \right) \left( \sqrt{1+\dfrac{1}{x^2} } +\sqrt{1-\dfrac{1}{x^2} } \right) } \\
= & \dfrac{1}{8} .
\end{align}$$

$571$.$\displaystyle \lim_{x\to 0} \dfrac{\sqrt{1+x\sin{x} } -1}{e^{x^2} -1} $.

解

$$\begin{align}
& \lim_{x\to 0} \dfrac{\sqrt{1+x\sin{x} } -1}{e^{x^2} -1} \\
= & \lim_{x\to 0} \dfrac{x\sin{x} }{(e^{x^2} -1)(\sqrt{1+x\sin{x} } +1)} \\
= & \lim_{x\to 0} \dfrac{\dfrac{\sin{x} }{x} }{\dfrac{e^{x^2} -1}{x^2} (\sqrt{1+x\sin{x} } +1)} \\
= & \dfrac{1}{2} .
\end{align}$$

$572$.$\displaystyle \lim_{x\to 0} \dfrac{\cos{(xe^x)} -\cos{(xe^{-x})} }{x^3} $.

解

$$\begin{align}
& \lim_{x\to 0} \dfrac{\cos{(xe^x)} -\cos{(xe^{-x})} }{x^3} \\
= & \lim_{x\to 0} \dfrac{-2\sin{\dfrac{x(e^x +e^{-x})}{2} \sin{\dfrac{x(e^x -e^{-x})}{2} } } }{x^3} \\
= & -2\lim_{x\to 0} \left[ \dfrac{\sin{\dfrac{x(e^x +e^{-x})}{2}} }{\dfrac{x(e^x +e^{-x})}{2} } \cdot \dfrac{\sin{\dfrac{x(e^x -e^{-x})}{2}} }{\dfrac{x(e^x -e^{-x})}{2} } \cdot \dfrac{x^2 (e^{4x} -1)}{4x^3e^{2x}} \right] \\
= & -2\lim_{x\to 0} \left( \dfrac{e^{4x} -1}{4x} \cdot \dfrac{1}{e^{2x}} \right) \\
= & -2.
\end{align}$$

$573$.$\displaystyle \lim_{x\to 0} (2e^{\frac{x}{x+1} } -1)^{\frac{x^2+1}{x} } $.

解

$$\begin{align}
& \lim_{x\to 0} (2e^{\frac{x}{x+1} } -1)^{\frac{x^2+1}{x} } \\
= & \lim_{x\to 0} \left\lbrace \left[ 1+2(e^{\frac{x}{x+1} } -1) \right]^{\frac{1}{2(e^{\frac{x}{x+1} } -1)} } \right\rbrace^{\frac{2(x^2+1)}{x+1} \cdot \frac{e^{\frac{x}{x+1} } -1}{\frac{x}{x+1} } } \\
= & e^2 .
\end{align}$$

$574$.$\displaystyle \lim_{x\to 1} (2-x)^{\sec{\frac{\pi x}{2} }} $.

解

$$\begin{align}
& \lim_{x\to 1} (2-x)^{\sec{\frac{\pi x}{2} }} \\
= & \lim_{x\to 1} [ 1+(-x+1) ]^{\frac{1}{1-x} \cdot \frac{\frac{\pi (x-1)}{2} }{\sin{\frac{\pi (x-1)}{2} } } \cdot \frac{2}{\pi } } \\
= & e^{\frac{2}{\pi } } .
\end{align}$$

$575$.$\displaystyle \lim_{x\to \frac{\pi }{2} } \dfrac{1-\sin{}^{\alpha +\beta } x}{\sqrt{(1-\sin{}^{\alpha } x)(1-\sin{}^{\beta } x)} } (\alpha > 0,\beta > 0) $.

解

$$\begin{align}
& \lim_{x\to \frac{\pi }{2} } \dfrac{1-\sin{}^{\alpha +\beta } x}{\sqrt{(1-\sin{}^{\alpha } x)(1-\sin{}^{\beta } x)} } \\
= & \lim_{x\to \frac{\pi }{2} } \dfrac{1-e^{(\alpha +\beta )\cdot \ln \sin{x} }}{\sqrt{(1-e^{\alpha \cdot \ln \sin{x} })(1-e^{\beta \cdot \ln \sin{x} }) } } \\
= & \lim_{x\to \frac{\pi }{2} } \left[ \left( \dfrac{1-e^{(\alpha +\beta )\cdot \ln \sin{x} }}{(\alpha +\beta )\cdot \ln \sin{x} } \right) \cdot \left( \dfrac{\alpha \cdot \ln \sin{x} }{e^{\alpha \ln \sin{x} }-1} \right)^{\frac{1}{2} } \cdot \left( \dfrac{\beta \cdot \ln \sin{x} }{e^{\beta \ln \sin{x} }-1} \right)^{\frac{1}{2} } \cdot \left( \dfrac{(\alpha +\beta )\cdot \ln \sin{x} }{\sqrt{\alpha \beta } \cdot \ln \sin{x} } \right) \right] \\
= & \dfrac{\alpha +\beta }{\sqrt{\alpha \beta } } .
\end{align}$$

双曲函数与反三角函数的极限计算

《习题集》中关于前三个双曲函数的定义和图像见习题$340(a),(b),(c)$，关于前四个反三角函数的图像见习题$311-314$（参见附录一）.

《习题集》中收入的关于这两类函数的极限计算题一般比较容易.

$576$.$(a)\displaystyle \lim_{x\to 0} \dfrac{\sinh{x} }{x} $；$(b)\displaystyle \lim_{x\to 0} \dfrac{\cosh{x} -1}{x^2} $；$(c)\displaystyle \lim_{x\to 0} \dfrac{\tanh{x} }{x} $（参考习题$340$）.

解$\quad (a)$

$$\begin{align}
& \lim_{x\to 0} \dfrac{\sinh{x} }{x} \\
= & \lim_{x\to 0} \dfrac{e^x-e^{-x}}{2x} \\
= & \lim_{x\to 0} \left( \dfrac{1}{2} \cdot \dfrac{e^x-1}{x} +\dfrac{1}{2} \cdot \dfrac{e^{-x}-1}{-x} \right) \\
= & 1.
\end{align}$$

$(b)$

$$\begin{align}
& \lim_{x\to 0} \dfrac{\cosh{x} -1}{x^2} \\
= & \lim_{x\to 0} \dfrac{e^x+e^{-x}-2}{2x^2} \\
= & \lim_{x\to 0} \dfrac{(1+x+\cdots +\dfrac{x^n}{n!} +o(x^n))+(1-x+\cdots +\dfrac{(-1)^n x^n}{n!} +o(x^n))-2}{2x^2} \\
= & \dfrac{1}{2} .
\end{align}$$

$(c)$

$$\begin{align}
& \lim_{x\to 0} \dfrac{\tanh{x} }{x} \\
= & \lim_{x\to 0} \dfrac{e^x-e^{-x}}{x(e^x+e^{-x})} \\
= & \lim_{x\to 0} \dfrac{e^{-x}(e^{2x}-1)}{xe^{-x}(e^{2x}+1)} \\
= & \lim_{x\to 0} \dfrac{e^{2x}-1}{2x} \cdot \dfrac{2}{e^{2x}+1} \\
= & 1.
\end{align}$$

$577$.$\displaystyle (a)\lim_{x\to 0} \dfrac{\sinh{}^2 x}{\ln \cosh{3x} } $（参考习题$340$）；$(b)\displaystyle \lim_{x\to +\infty } \dfrac{\sinh{\sqrt{x^2+x} } -\sinh{\sqrt{x^2-x} } }{\cosh{x} } $.

解$\quad (a)$

$$\begin{align}
& \lim_{x\to 0} \dfrac{\sinh{}^2 x}{\ln \cosh{3x} } \\
= & \lim_{x\to 0} \dfrac{\dfrac{\left( e^{2x} -1\right)^2 }{4e^{2x}} }{\ln \left[ 1+\dfrac{1}{2} \left( e^{\frac{3}{2} x} -e^{-\frac{3}{2} x} \right)^2 \right] } \\
= & \lim_{x\to 0} \left[ \left( \dfrac{e^{2x}-1}{2x} \right)^2 \cdot \dfrac{\dfrac{1}{2} \left( e^{\frac{3}{2} x} -e^{-\frac{3}{2} x} \right)^2 \cdot e^x}{\ln \left[ 1+\dfrac{1}{2} \left( e^{\frac{3}{2} x} -e^{-\frac{3}{2} x} \right)^2 \right] } \cdot \left( \dfrac{3x}{e^{3x} -1} \right)^2 \cdot \dfrac{2}{9} \right] \\
= & \dfrac{2}{9} .
\end{align}$$

$(b)$分子是$\infty -\infty $型的不定式.按照定义将双曲函数用指数函数表示，并将分子分母同除以适当的无穷大量即可计算如下：

$$\begin{align}
& \lim_{x\to +\infty } \dfrac{\dfrac{e^{\sqrt{x^2+x} } -e^{-\sqrt{x^2+x} } }{2} -\dfrac{e^{\sqrt{x^2-x} } -e^{-\sqrt{x^2-x} } }{2} }{\dfrac{e^x +e^{-x}}{2} } \\
= & \lim_{x\to +\infty } (e^{\sqrt{x^2+x} -x} -e^{\sqrt{x^2-x} -x}) \\
= & \lim_{x\to +\infty } (e^{\frac{x}{\sqrt{x^2+x} +x} } -e^{\frac{-x}{\sqrt{x^2-x} +x} }) \\
= & e^{\frac{1}{2} } -e^{-\frac{1}{2} } \\
= & 2\sinh{\dfrac{1}{2} } .
\end{align}$$

$578$.$\displaystyle (a)\lim_{x\to a} \dfrac{\sinh{x} -\sinh{a} }{x-a} $；$(b)\displaystyle \lim_{x\to a} \dfrac{\cosh{x} -\cosh{a} }{x-a} $；$(c)\displaystyle \lim_{x\to 0} \dfrac{\ln \cosh{x} }{\ln \cos{x} } $.

解$\quad (a)$

$$\begin{align}
& \lim_{x\to a} \dfrac{\sinh{x} -\sinh{a} }{x-a} \\
= & \lim_{x\to a} \dfrac{\dfrac{e^x-e^{-x}}{2} -\dfrac{e^a-e^{-a}}{2}}{x-a} \\
= & \lim_{x\to a} \dfrac{\dfrac{e^x-e^{-x}-(e^a-e^{-a})}{2} }{x-a} \\
= & \lim_{x\to a} \dfrac{\dfrac{e^x-e^{a}+e^{-a}-e^{-x}}{2} }{x-a} \\
= & \lim_{x\to a} \dfrac{\dfrac{e^{\frac{x-a}{2} +\frac{x+a}{2} }-e^{\frac{-x+a}{2} +\frac{x+a}{2} }+e^{\frac{x-a}{2} +(-\frac{x+a}{2} )}-e^{\frac{-x+a}{2} +(-\frac{x+a}{2} )}}{2} }{x-a} \\
= & \lim_{x\to a} \dfrac{\left( e^{\frac{x-a}{2} }-e^{\frac{-x+a}{2} }\right) \cdot \dfrac{e^{\frac{x+a}{2} }+e^{-\frac{x+a}{2} }}{2} }{x-a} \\
= & \lim_{x\to a} \dfrac{e^{\frac{x-a}{2} }-e^{\frac{-x+a}{2} }}{x-a} \cdot \lim_{x\to a} \dfrac{e^{\frac{x+a}{2} }+e^{-\frac{x+a}{2} }}{2} \\
= & \lim_{x\to a} \left( \dfrac{e^{\frac{x-a}{2} }-1}{2\cdot \dfrac{x-a}{2} } +\dfrac{e^{\frac{-x+a}{2} } -1}{2\cdot \dfrac{-x+a}{2} } \right) \cdot \lim_{x\to a} \cosh{\dfrac{x+a}{2}} \\
= & \cosh{a} .
\end{align}$$

$(b)$

$$\begin{align}
& \lim_{x\to a} \dfrac{\cosh{x} -\cosh{a} }{x-a} \\
= & \lim_{x\to a} \dfrac{\dfrac{e^x+e^{-x}}{2} -\dfrac{e^a+e^{-a}}{2}}{x-a} \\
= & \lim_{x\to a} \dfrac{\dfrac{e^x+e^{-x}-(e^a+e^{-a})}{2} }{x-a} \\
= & \lim_{x\to a} \dfrac{\dfrac{e^x-e^{a}-e^{-a}+e^{-x}}{2} }{x-a} \\
= & \lim_{x\to a} \dfrac{\dfrac{e^{\frac{x-a}{2} +\frac{x+a}{2} }-e^{\frac{-x+a}{2} +\frac{x+a}{2} }-e^{\frac{x-a}{2} +(-\frac{x+a}{2} )}+e^{\frac{-x+a}{2} +(-\frac{x+a}{2} )}}{2} }{x-a} \\
= & \lim_{x\to a} \dfrac{\left( e^{\frac{x-a}{2} }-e^{\frac{-x+a}{2} }\right) \cdot \dfrac{e^{\frac{x+a}{2} }-e^{-\frac{x+a}{2} }}{2} }{x-a} \\
= & \lim_{x\to a} \dfrac{e^{\frac{x-a}{2} }-e^{\frac{-x+a}{2} }}{x-a} \cdot \lim_{x\to a} \dfrac{e^{\frac{x+a}{2} }-e^{-\frac{x+a}{2} }}{2} \\
= & \lim_{x\to a} \left( \dfrac{e^{\frac{x-a}{2} }-1}{2\cdot \dfrac{x-a}{2} } +\dfrac{e^{\frac{-x+a}{2} } -1}{2\cdot \dfrac{-x+a}{2} } \right) \cdot \lim_{x\to a} \sinh{\dfrac{x+a}{2}} \\
= & \sinh{a} .
\end{align}$$

$(c)$由于，

$$\begin{align}
& \lim_{x\to 0} \left( \left[ \dfrac{e^x+e^{-x}}{2} -1\right] \cdot \dfrac{1}{(\cos{x} -1 )} \right) \\
= & \lim_{x\to 0} \dfrac{e^{-x} (e^{2x} -2e^x+1)}{2(\cos{x} -1)} \\
= & \lim_{x\to 0} \dfrac{e^{-x}(e^{x} -1)^2}{2(\cos{x} -1)} \\
= & \lim_{x\to 0} \dfrac{e^{-x}(\dfrac{e^{x} -1}{x} )^2 \cdot x^2}{2(\cos{x} -1)} \\
= & \lim_{x\to 0} \dfrac{e^{-x}(\dfrac{e^{x} -1}{x} )^2 \cdot x^2}{2(-\dfrac{1}{2} x^2)} \\
= & -1,
\end{align}$$

因此，

$$\begin{align}
& \lim_{x\to 0} \dfrac{\ln \cosh{x} }{\ln \cos{x} } \\
= & \lim_{x\to 0} \dfrac{\ln \dfrac{e^x+e^{-x}}{2} }{\ln (1+\cos{x} -1)} \\
= & \lim_{x\to 0} \dfrac{\ln \dfrac{e^x+e^{-x}}{2} }{(\cos{x} -1)} \\
= & \lim_{x\to 0} \ln \left( 1+\dfrac{e^x+e^{-x}}{2} -1\right)^{\frac{1}{\cos{x} -1} } \\
= & \lim_{x\to 0} \ln \left( 1+\dfrac{e^x+e^{-x}}{2} -1\right)^{\frac{2}{e^x+e^{-x} -2} \cdot \left( \frac{e^x+e^{-x}}{2} -1\right) \cdot \frac{1}{\cos{x} -1} } \\
= & \ln e^{-1} \\
= & -1.
\end{align}$$

$579$.$(a)\displaystyle \lim_{x\to +\infty } (x-\ln \cosh{x} ) $；$(b)\displaystyle \lim_{x\to 0} \dfrac{e^{\sin{2x} } -e^{\sin{x} }}{\tanh{x} } $.

解$\quad (a)$

$$\begin{align}
& \lim_{x\to +\infty } (x-\ln \cosh{x} ) \\
= & \lim_{x\to +\infty } \left(x-\ln \dfrac{e^{2x}+1}{2e^x} \right) \\
= & \lim_{x\to +\infty } [2x+\ln 2-\ln (1+e^{2x})] \\
= & \lim_{x\to +\infty } [\ln 2-\ln (e^{-2x} +1)] \\
= & \ln 2.
\end{align}$$

$\quad (b)$

$$\begin{align}
& \lim_{x\to 0} \dfrac{e^{\sin{2x} } -e^{\sin{x} }}{\tanh{x} } \\
= & \lim_{x\to 0} \dfrac{(e^{\sin{2x} } -e^{\sin{x} })(e^{2x} +1)}{(e^{2x} -1)} \\
= & \lim_{x\to 0} \dfrac{\left( \dfrac{e^{\sin{2x} } -1}{\sin{2x} } \cdot \dfrac{\sin{2x}}{2x} -\dfrac{e^{\sin{x} } -1}{\sin{x} } \cdot \dfrac{\sin{x}}{x} \cdot \dfrac{1}{2} \right) (e^{2x} +1)}{\dfrac{(e^{2x} -1)}{2x} } \\
= & \dfrac{2\left( 1-\dfrac{1}{2} \right) }{1} \\
= & 1.
\end{align}$$

$580$.$\displaystyle \lim_{n\to \infty } \left( \dfrac{\cosh{\dfrac{\pi }{n} } }{\cos{\dfrac{\pi }{n} } } \right)^{n^2} $.

解

$$\begin{align}
& \left( \dfrac{\cosh{\dfrac{\pi }{n} } }{\cos{\dfrac{\pi }{n} } } \right)^{n^2} \\
= & \left( \dfrac{e^{\frac{\pi }{n} } +e^{-\frac{\pi }{n} }}{2\cos{\dfrac{\pi }{n} } } \right)^{n^2} \\
= & \left( 1+\dfrac{1}{\dfrac{2\cos{\dfrac{\pi }{n} } }{e^{\frac{\pi }{n} } +e^{-\frac{\pi }{n} } -2\cos{\dfrac{\pi }{n} } } } \right)^{\frac{2\cos{\frac{\pi }{n} } }{e^{\frac{\pi }{n} } +e^{-\frac{\pi }{n} } -2\cos{\frac{\pi }{n} } } \cdot \frac{n^2 \left( e^{\frac{\pi }{n} } +e^{-\frac{\pi }{n} } -2\cos{\frac{\pi }{n} } \right) }{2\cos{\frac{\pi }{n} } } } ,
\end{align}$$

因为，

$$\begin{align}
& n^2 \left( e^{\frac{\pi }{n} } +e^{-\frac{\pi }{n} } -2\cos{\dfrac{\pi }{n} } \right) \\
= & n^2 \left[ (e^{\frac{\pi }{2n} } +e^{-\frac{\pi }{2n} } )^2 +2(1-\cos{\dfrac{\pi }{n} } ) \right] \\
= & n^2 \left[ (e^{\frac{\pi }{2n} } +e^{-\frac{\pi }{2n} } )^2 +4\sin{}^2 \dfrac{\pi }{2n} \right] \\
= & \left( \dfrac{e^{\frac{\pi }{2n} } -1}{\dfrac{\pi }{2n} } \cdot \dfrac{\pi }{2} +\dfrac{e^{-\frac{\pi }{2n} } -1}{-\dfrac{\pi }{2n} } \cdot \dfrac{\pi }{2} \right)^2 +\pi^2 \left( \dfrac{\sin{\dfrac{\pi }{2n} } }{\dfrac{\pi }{2n} } \right)^2 \\
\to & 2\pi^2 (n\to \infty ),
\end{align}$$

所以，$\displaystyle \lim_{n\to \infty } \left( \dfrac{\cosh{\dfrac{\pi }{n} } }{\cos{\dfrac{\pi }{n} } } \right)^{n^2} =e^{\pi^2} $.

$581$.$\displaystyle \lim_{x\to \infty } \arcsin{\dfrac{1-x}{1+x} } $.

解$\quad \displaystyle \lim_{x\to \infty } \arcsin{\dfrac{1-x}{1+x} } =\arcsin{(-1)} =-\dfrac{\pi }{2} $.

$582$.$\displaystyle \lim_{x\to +\infty } \arccos{(\sqrt{x^2+x} -x)} $.

解$\quad \displaystyle \lim_{x\to +\infty } \arccos{(\sqrt{x^2+x} -x)} =\lim_{x\to +\infty } \arccos{\dfrac{x}{\sqrt{x^2+x} +x} } =\arccos{\dfrac{1}{2} } =\dfrac{\pi }{3} $.

$583$.$\displaystyle \lim_{x\to 2} \arctan{\dfrac{x-4}{(x-2)^2} } $.

解$\quad \displaystyle \lim_{x\to 2} \arctan{\dfrac{x-4}{(x-2)^2} } =-\dfrac{\pi }{2} $.

$584$.$\displaystyle \lim_{x\to -\infty } \mathrm{arccot} \;\dfrac{x}{\sqrt{1+x^2} } $.

解$\quad \displaystyle \lim_{x\to -\infty } \mathrm{arccot} \;\dfrac{x}{\sqrt{1+x^2} } =\mathrm{arccot} \;(-1)=\dfrac{3\pi }{4} $.

$585$.$\displaystyle \lim_{h\to 0} \dfrac{\arctan{(x+h)} -\arctan{x} }{h} $.

解$\quad $这里的困难在于如何处理分子.计算分子的正切函数值就有

$$\tan [\arctan{(x+h)} -\arctan{x} ] =\dfrac{h}{1+(x+h)x} .$$

可见当$h$充分小时分子的绝对值也很小，因此得到

$$\arctan{(x+h)} -\arctan{x} =\arctan{\dfrac{h}{1+(x+h)x} } .$$

从等价关系$\tan{x} \sim x(x\to 0)$（即习题$474(b)$），可见也有$\arctan{x} \sim x(x\to 0)$.

综合以上两点可见本题的极限为$\dfrac{1}{1+x^2} $.

$586$.$\displaystyle \lim_{x\to 0} \dfrac{\ln \dfrac{1+x}{1-x} }{\arctan{(1+x)} -\arctan{(1-x)} } $.

解

$$\begin{align}
& \lim_{x\to 0} \dfrac{\ln \dfrac{1+x}{1-x} }{\arctan{(1+x)} -\arctan{(1-x)} } \\
= & \lim_{x\to 0} \left[ \dfrac{\ln \left( 1+\dfrac{2x}{1-x} \right) }{\dfrac{2x}{1-x} } \cdot \dfrac{\dfrac{2x}{2-x^2} }{\arctan{\dfrac{2x}{2-x^2} } } \cdot \dfrac{2-x^2}{1-x} \right] \\
= & 2.
\end{align}$$

$587$.$\displaystyle \lim_{n\to \infty } \left[ n\arctan \dfrac{1}{n(x^2+1)+x} \cdot \tan{}^n \left( \dfrac{\pi }{4} +\dfrac{x}{2n} \right) \right] $.

解

$$\begin{align}
& \lim_{n\to \infty } \left[ n\arctan \dfrac{1}{n(x^2+1)+x} \cdot \tan{}^n \left( \dfrac{\pi }{4} +\dfrac{x}{2n} \right) \right] \\
= & \lim_{n\to \infty } \left[ \dfrac{\arctan \dfrac{1}{n(x^2+1)+x} }{\dfrac{1}{n(x^2+1)+x} } \cdot \dfrac{n}{n(x^2+1)+x} \cdot \left( 1+\dfrac{1}{\dfrac{1-\tan{\dfrac{x}{2n} } }{2\tan{\dfrac{x}{2n} }} } \right)^{\frac{1-\tan{\frac{x}{2n} } }{2\tan{\frac{x}{2n} } } \cdot \frac{\tan{\frac{x}{2n} } }{\frac{x}{2n} } \cdot \frac{x}{1-\tan{\frac{x}{2n} } } } \right] \\
= & \dfrac{e^x}{1+x^2} .
\end{align}$$

$588$.$\displaystyle \lim_{x\to \infty } x\left( \dfrac{\pi }{4} -\arctan{\dfrac{x}{x+1} } \right) $.

解

$$\begin{align}
& \lim_{x\to \infty } x\left( \dfrac{\pi }{4} -\arctan{\dfrac{x}{x+1} } \right) \\
= & \lim_{x\to \infty } x\arctan{\dfrac{1}{2x+1} } \\
= & \lim_{x\to \infty } \left( \dfrac{\arctan{\dfrac{1}{2x+1} } }{\dfrac{1}{2x+1}} \cdot \dfrac{x}{2x+1} \right) \\
= & \dfrac{1}{2} .
\end{align}$$

$589$.$\displaystyle \lim_{x\to +\infty } x\left( \dfrac{\pi }{2} -\arcsin{\dfrac{x}{\sqrt{x^2+1} } } \right) $.

解

$$\begin{align}
& \lim_{x\to +\infty } x\left( \dfrac{\pi }{2} -\arcsin{\dfrac{x}{\sqrt{x^2+1} } } \right) \\
= & \lim_{x\to +\infty } x\arcsin{\dfrac{1}{\sqrt{x^2+1} } } \\
= & \lim_{x\to \infty } \left( \dfrac{\arcsin{\dfrac{1}{\sqrt{x^2+1} } } }{\dfrac{1}{\sqrt{x^2+1} } } \cdot \dfrac{x}{\sqrt{x^2+1} } \right) \\
= & 1 .
\end{align}$$

$590$.$\displaystyle \lim_{n\to \infty } \left[ 1+\dfrac{(-1)^n}{n} \right]^{\csc{(\pi \sqrt{1+n^2} )}} $.

解

$$\begin{align}
& \lim_{n\to \infty } \left[ 1+\dfrac{(-1)^n}{n} \right]^{\csc{(\pi \sqrt{1+n^2} )}} \\
= & \lim_{n\to \infty } \left[ 1+\dfrac{(-1)^n}{n} \right]^{\frac{n}{(-1)^n} \cdot \frac{(-1)^n}{n\sin{(\pi \sqrt{1+n^2} )}} } \\
= & \lim_{n\to \infty } \left[ 1+\dfrac{(-1)^n}{n} \right]^{\frac{n}{(-1)^n} \cdot \frac{-1}{n\sin{(n\pi -\pi \sqrt{1+n^2} )}} } \\
= & \lim_{n\to \infty } \left[ 1+\dfrac{(-1)^n}{n} \right]^{\frac{n}{(-1)^n} \cdot \frac{n\pi -\pi \sqrt{1+n^2} }{\sin{(n\pi -\pi \sqrt{1+n^2} )}} \cdot \frac{1}{n(\pi \sqrt{1+n^2} -n\pi ) } } \\
= & e^{\lim\limits_{n\to +\infty } \frac{\sqrt{n^2+1} +n}{n\pi (n^2+1-n^2)} } \\
= & e^{\frac{2}{\pi } } (n\pi -\pi \sqrt{1+n^2} \to 0).
\end{align}$$

$591$.$\displaystyle (a)\lim_{x\to 0} \dfrac{1}{x^{100}} e^{-\frac{1}{x^2} } $；$(b)\displaystyle \lim_{x\to +0} x\ln x$.

解$\quad (a)$令$y=\dfrac{1}{x}$，则

$$\lim_{x\to 0} \dfrac{1}{x^{100}} e^{-\frac{1}{x^2} } =\lim_{y\to \infty } \dfrac{y^{100}}{e^{y^2}} =\lim_{y\to \infty } \dfrac{(y^2)^{50}}{e^{y^2}} =0.$$

$(b)$设$y=\dfrac{1}{x} $，则

$$\lim_{x\to +0} x\ln x=\lim_{y\to +\infty } \dfrac{-\ln y}{y} =0.$$

求下列极限：

$602$.$\displaystyle \lim_{x\to 0} x\sqrt{\cos{\dfrac{1}{x} } } $.

解$\quad $因为$\sqrt{\cos{\dfrac{1}{x} } } $为有界函数，所以，$\displaystyle \lim_{x\to 0} x\sqrt{\cos{\dfrac{1}{x} } } =0$.

$604$.$\displaystyle \lim_{n\to \infty } \sin{(\pi \sqrt{n^2+1} )} $.

解

$$\begin{align}
& \lim_{n\to \infty } \sin{(\pi \sqrt{n^2+1} )} \\
= & \lim_{n\to \infty } (-1)^n \sin{(\pi \sqrt{n^2+1} -n\pi )} \\
= & \lim_{n\to \infty } (-1)^n \sin{\dfrac{\pi }{\sqrt{n^2+1} +n} } \\
= & 0.
\end{align}$$

$605$.$\displaystyle \lim_{n\to \infty } \sin{}^2 (\pi \sqrt{n^2+n} ) $.

解

$$\begin{align}
& \lim_{n\to \infty } \sin{}^2 (\pi \sqrt{n^2+n} ) \\
= & \lim_{n\to \infty } \dfrac{1}{2} [1-\cos{(2\pi \sqrt{n^2+n})} ] \\
= & \lim_{n\to \infty } \dfrac{1}{2} \left\lbrace 1-\cos{[2\pi (\sqrt{n^2+n} -n)]} \right\rbrace \\
= & 1.
\end{align}$$

杂题

这里的习题数量不多，但有多类型，下面先浏览一下其内容.

习题$592-601$都是（广义）单侧极限的计算题，其中包括$x\to a\pm 0$和$x\to \pm \infty $在内，其中的计算没有特殊困难.

习题$613-625$是函数序列研究中需要用到的内容.假设在某个区间上定义有函数序列$\lbrace f_n (x)\rbrace $，且在区间的每个点上存在极限$\displaystyle \lim_{n\to \infty } f_n (x)$，这样就得到了函数序列的极限函数.这些习题就是要求计算出极限函数，并作出其图像（其中习题$624$是含有连续参数$t$的对应问题）.这里的计算和作图也都比较容易.

习题$626-627$是关于斜渐近线的定义和训练.这在一般教科书中都有，相应的计算题和作图都不难（在$\S 1.4$中已经有大量的这类习题）.

习题$641-644$是涉及函数的点振幅和函数的上下极限的题，计算均较容易.

下面只对于习题$628-636$作讲解，其中含有与无穷级数、无穷乘积有关以及更广泛的一些极限计算题，对于后者还专门介绍了一个有用的定理.

这里的问题是计算如下形式的数列极限：

$$\lim_{n\to \infty } (x_{1n} +x_{2n} +\cdots +x_{nn} )=\lim_{n\to \infty } \sum_{m=1}^n x_{mn} ,\label{7} \tag{1.39}$$

其中$\lbrace x_{mn} \rbrace $是具有双下标的数列，$n$取所有正整数，而在下标$n$给定之后的下标$m$则只需要取$1,2,\cdots ,n$.问题$\eqref{7}$的一个变型是用相乘代替相加，即求如下数列极限：

$$\lim_{n\to \infty } (x_{1n} \cdot x_{2n} \cdot \cdots \cdot x_{nn} )=\lim_{n\to \infty } \prod_{m=1}^n x_{mn} ,\label{8} \tag{1.40}$$

其中双下标的意义与$\eqref{7}$相同.

在每一个$x_{mn} > 0$的前提下，可以取对数将问题$\eqref{8}$转化为问题$\eqref{7}$.

事实上这样的数列极限问题早在$\S 1.2$就已经遇到，例如习题$51-57$，$68$，$72$，$77-80$，$82-85$等等都是如此.

若$x_{mn}$与$n$无关，即只有一个下标$m$时，$n$只以求和或求乘积的项数出现.这就是今后要遇到的无穷级数和无穷乘积的计算题（见《习题集》第五章）.例如$\S 1.2$中的习题$56$，$57$，$68$，$72$，$77-80$，$82-85$，以及本节的习题$629-630$，都属于这个子类.由于这类问题将在第五章作专门研究，因此从略.

下面主要介绍习题$631-636$，即$x_{mn}$确实为双下标的情况.

习题$631$提出了计算这类问题的一种方法，其中的$x_{mn} =\varphi (\alpha_{mn} )$，$\varphi $为某个具有一定性质的函数，$\lbrace \alpha_{mn} \rbrace $为具有双下标的数列，$\rightrightarrows $是一致收敛的记号.

$592$.$(a)\displaystyle \lim_{x\to -\infty } (\sqrt{x^2+x} -x) $；$(b)\displaystyle \lim_{x\to +\infty } (\sqrt{x^2+x} -x) $.

解$\quad (a)\displaystyle \lim_{x\to -\infty } (\sqrt{x^2+x} -x) =+\infty $;

$(b)\displaystyle \lim_{x\to +\infty } (\sqrt{x^2+x} -x) =\lim_{x\to \infty } \dfrac{x}{\sqrt{x^2+x} +x} =\dfrac{1}{2} $.

$593$.$(a)\displaystyle \lim_{x\to -\infty } (\sqrt{1+x+x^2} -\sqrt{1-x+x^2} ) $；$(b)\displaystyle \lim_{x\to +\infty } (\sqrt{1+x+x^2} -\sqrt{1-x+x^2} ) $.

解$\quad (a)$

$$\begin{align}
& \lim_{x\to -\infty } (\sqrt{1+x+x^2} -\sqrt{1-x+x^2} ) \\
= & \lim_{x\to -\infty } \dfrac{2x}{\sqrt{1+x+x^2} +\sqrt{1-x+x^2} } \\
= & \lim_{x\to -\infty } \dfrac{-2}{\sqrt{\dfrac{1}{x^2} +\dfrac{1}{x} +1} +\sqrt{\dfrac{1}{x^2} -\dfrac{1}{x} +1} } \\
= & -1.
\end{align}$$

$(b)$

$$\begin{align}
& \lim_{x\to +\infty } (\sqrt{1+x+x^2} -\sqrt{1-x+x^2} ) \\
= & \lim_{x\to +\infty } \dfrac{2x}{\sqrt{1+x+x^2} +\sqrt{1-x+x^2} } \\
= & \lim_{x\to +\infty } \dfrac{2}{\sqrt{\dfrac{1}{x^2} +\dfrac{1}{x} +1} +\sqrt{\dfrac{1}{x^2} -\dfrac{1}{x} +1} } \\
= & 1.
\end{align}$$

$594$.设$f(x)=\ln \dfrac{x+\sqrt{x^2+a^2} }{x+\sqrt{x^2+b^2} } $，求$h=\displaystyle \lim_{x\to +\infty } f(x)-\lim_{x\to -\infty } f(x)$.

解$\quad $由于

$$\begin{align}
& \lim_{x\to +\infty } f(x) \\
= & \lim_{x\to +\infty } \ln \dfrac{x+\sqrt{x^2+a^2} }{x+\sqrt{x^2+b^2} } \\
= & \lim_{x\to +\infty } \ln \dfrac{1+\sqrt{1+\dfrac{a^2}{x^2} } }{1+\sqrt{1+\dfrac{b^2}{x^2} } } \\
= & 0,
\end{align}$$

及

$$\begin{align}
& \lim_{x\to -\infty } f(x) \\
= & \lim_{x\to -\infty } \ln \dfrac{x+\sqrt{x^2+a^2} }{x+\sqrt{x^2+b^2} } \\
= & \lim_{x\to -\infty } \ln \dfrac{1-\sqrt{1+\dfrac{a^2}{x^2} } }{1-\sqrt{1+\dfrac{b^2}{x^2} } } \\
= & \lim_{x\to -\infty } \ln \dfrac{\left( 1+\dfrac{a^2}{x^2} \right)^{\frac{1}{2} } -1}{\left( 1+\dfrac{b^2}{x^2} \right)^{\frac{1}{2} } -1} \\
= & \lim_{x\to -\infty } \ln \left( \dfrac{\left( 1+\dfrac{a^2}{x^2} \right)^{\frac{1}{2} } -1}{\dfrac{a^2}{x^2} } \cdot \dfrac{\dfrac{b^2}{x^2} }{\left( 1+\dfrac{b^2}{x^2} \right)^{\frac{1}{2} } -1} \cdot \dfrac{\dfrac{a^2}{x^2} }{\dfrac{b^2}{x^2} }\right) \\
= & \lim_{x\to -\infty } \ln \left( \dfrac{1}{2} \cdot \dfrac{1}{\dfrac{1}{2} } \cdot \dfrac{a^2}{b^2} \right) \\
= & \ln \dfrac{a^2}{b^2} ,
\end{align}$$

故，$h=\displaystyle \lim_{x\to +\infty } f(x)-\lim_{x\to -\infty } f(x)=0-\ln \dfrac{a^2}{b^2} =\ln \dfrac{b^2}{a^2} $.

$595$.$(a)\displaystyle \lim_{x\to 1-0} \arctan{\dfrac{1}{1-x} } $；$(b)\displaystyle \lim_{x\to 1+0} \arctan{\dfrac{1}{1-x} } $.

解$\quad (a)\displaystyle \lim_{x\to 1-0} \arctan{\dfrac{1}{1-x} } =\dfrac{\pi }{2} $；

$(b)\displaystyle \lim_{x\to 1+0} \arctan{\dfrac{1}{1-x} } =-\dfrac{\pi }{2} $.

$596$.$(a)\displaystyle \lim_{x\to 1-0} \dfrac{1}{1+e^{\frac{1}{x} }} $；$(b)\displaystyle \lim_{x\to 1+0} \dfrac{1}{1+e^{\frac{1}{x} }} $.

解$\quad (a)\displaystyle \lim_{x\to 1-0} \dfrac{1}{1+e^{\frac{1}{x} }} =1$；

$(b)\displaystyle \lim_{x\to 1+0} \dfrac{1}{1+e^{\frac{1}{x} }} =0$.

$597$.$(a)\displaystyle \lim_{x\to -\infty } \dfrac{\ln (1+e^x)}{x} $；$(b)\displaystyle \lim_{x\to +\infty } \dfrac{\ln (1+e^x)}{x} $.

解$\quad (a)\displaystyle \lim_{x\to -\infty } \dfrac{\ln (1+e^x)}{x} =\lim_{x\to -\infty } \left[ \dfrac{\ln (1+e^x)}{e^x} \cdot \dfrac{e^x}{x} \right] =0$；

$(b)\displaystyle \lim_{x\to +\infty } \dfrac{\ln (1+e^x)}{x} =\lim_{x\to +\infty } \left[ 1+\dfrac{\ln (e^{-x} +1)}{x} \right] =1 $.

$598$.证明：

$(a)$当$x\to -\infty $时，$\dfrac{2x}{1+x} \to 2+0$；

$(b)$当$x\to +\infty $时，$\dfrac{2x}{1+x} \to 2-0$.

证$\quad (a)$当$x < 0$时，及当$\vert x\vert $充分大以后，$\dfrac{2x}{1+x} > 2$.于是，当$x\to -\infty $时，$\dfrac{2x}{1+x} \to 2+0 $；

$(b)$当$x > 0$时，$0 < \dfrac{2x}{1+x} < 2$.于是，当$x\to +\infty $时，$\dfrac{2x}{1+x} \to 2-0$.

$599$.证明：

$(a)$当$x\to -0 $时，$2^x \to 1-0$；

$(b)$当$x\to +0 $时，$2^x \to 1+0$.

证$\quad (a)$当$x < 0$时，$0 < 2^x < 1$.于是，当$x\to -0 $时，$2^x \to 1-0 $；

$(b)$当$x > 0$时，$2^x >1$.于是，当$x\to +0 $时，$\dfrac{2x}{1+x} \to 1+0$.

$600$.设$f(x)=x+[x^2] $，求$f(1)$，$f(1-0)$，$f(1+0)$.

解$\quad f(1)=2$；

$f(1-0)=\displaystyle \lim_{x\to 1-0} (x+[x^2])=1+0=1$；

$f(1+0)=\displaystyle \lim_{x\to 1+0} (x+[x^2])=1+1=2$.

$601$.设$f(x)=\mathrm{sgn} (\sin{\pi x} )$，求$f(n)$，$f(n-0)$，$f(n+0)(n=0,\pm 1,\cdots )$.

解$\quad f(n)=0$；

$f(n-0)=\displaystyle \lim_{x\to n-0} \mathrm{sgn} (\sin{\pi x} )=(-1)^{n-1}$；

$f(n+0)=\displaystyle \lim_{x\to n+0} \mathrm{sgn} (\sin{\pi x} )=(-1)^n$.

$603$.$\displaystyle \lim_{x\to 0} x\left[ \dfrac{1}{x} \right] $.

解$\quad $因为

$$\dfrac{1}{x} -1 < \left[ \dfrac{1}{x} \right] \leqslant \dfrac{1}{x} (x\neq 0),$$

当$x > 0$时

$$1-x < x\left[ \dfrac{1}{x} \right] \leqslant 1,$$

当$x < 0$时

$$1-x > x\left[ \dfrac{1}{x} \right] \geqslant 1,$$

于是，$\displaystyle \lim_{x\to 0} x\left[ \dfrac{1}{x} \right] =1$.

作下列函数的图像：

$613$.$(a)y=1-x^{100} $；$(b)y=\displaystyle \lim_{n\to \infty } (1-x^{2n}) (-1\leqslant x\leqslant 1)$.

解$\quad (a)$如图所示.它关于$y$轴对称.

$(b)y=\displaystyle \lim_{n\to \infty } (1-x^{2n})=\begin{cases} 1, & \vert x\vert < 1,\\ 0 & \vert x\vert =1.\end{cases}$如图所示.

$614$.$(a)y=\dfrac{x^{100}}{1+x^{100}} (x\geqslant 0)$；$(b)y=\displaystyle \lim_{n\to \infty } \dfrac{x^n}{1+x^n} (x\geqslant 0) $.

解$\quad (a)$如图所示.

$(b)y=\displaystyle \displaystyle \lim_{n\to \infty } \dfrac{x^n}{1+x^n}=\begin{cases} 0, & 0\leqslant x < 1,\\ \dfrac{1}{2} & x= 1, \\ 1 & 1 < x < +\infty . \end{cases}$ 如图所示.

$615$.$y=\displaystyle \lim_{n\to \infty } \dfrac{x^n -x^{-n}}{x^n +x^{-n}} (x\neq 0)$.

解$\quad $因为$y=\displaystyle \lim_{n\to \infty } \dfrac{x^{2n} -1}{x^{2n} +1} $，所以，$y=\begin{cases} -1, & \vert x\vert < 1 ,\\ 0 & \vert x\vert = 1, \\ 1 & \vert x\vert > 1 . \end{cases}$如图所示.

$616$.$y=\displaystyle \lim_{n\to \infty } \sqrt{x^2 +\dfrac{1}{n^2} } $.

解$\quad y=\sqrt{x^2} =\vert x\vert $.如图所示.

$617$.$y=\displaystyle \lim_{n\to \infty } \sqrt[n]{1+x^n } (x\geqslant 0)$.

解$\quad y=\begin{cases} 1, & 0\leqslant x \leqslant 1,\\ x & x > 1.\end{cases}$如图所示.

$618$.$y=\displaystyle \lim_{n\to \infty } \sqrt[n]{1+x^n +\left( \dfrac{x^2}{2} \right)^n } (x\geqslant 0)$.

解$\quad y=\begin{cases} 1, & 0\leqslant x \leqslant 1,\\ x & 1 < x < 2,\\ \dfrac{x^2}{2} , & 2\leqslant x < +\infty .\end{cases}$如图所示.

$619$.$y=\displaystyle \lim_{n\to \infty } \dfrac{x^{n+2}}{\sqrt{2^{2n} +x^{2n}} } (x\geqslant 0)$.

解$\quad y=\begin{cases} 0, & 0\leqslant x < 2,\\ 2\sqrt{2} & x=2,\\ x^2 , & x > 2 .\end{cases}$如图所示.

$620$.$(a)y=\sin{}^{1000} x$；$(b)y=\displaystyle \lim_{n\to \infty } \sin{}^{2n} x$.

解$\quad (a)$如图所示.其图像始终在$Ox$轴上方.

$(b)y=\begin{cases} 0, & x\neq (2k+1)\dfrac{\pi }{2} ,\\ 1, & x=(2k+1)\dfrac{\pi }{2} .\end{cases} (k=0,\pm 1,\pm 2 ,\cdots )$如图所示.

$621$.$y=\displaystyle \lim_{n\to \infty } \dfrac{\ln (2^n +x^n)}{n} (x\geqslant 0)$.

解$\quad y=\begin{cases} \ln 2, & 0\leqslant x\leqslant 2 ,\\ \ln x, & 2 < x < +\infty .\end{cases}$如图所示.

$622$.$y=\displaystyle \lim_{n\to \infty } (x-1)\arctan{x^n} $.

解$\quad y=\begin{cases} 0, & -1 < x\leqslant 1 ,\\ \dfrac{\pi }{2} , & x > 1 .\end{cases}$如图所示.

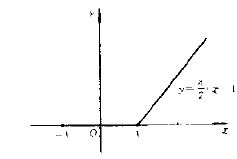
$623$.$y=\displaystyle \lim_{n\to \infty } \sqrt[n]{1+e^{n(x+1)}} $.

解$\quad y=\begin{cases} 1, & x\leqslant -1 ,\\ e^{x+1} , & x > -1 .\end{cases}$如图所示.

$624$.$(a)y=\displaystyle \lim_{t\to +\infty } \dfrac{x+e^{tx}}{1+e^{tx}} $；$(b)y=\displaystyle \lim_{t\to x} \dfrac{1}{t-x} \ln \dfrac{t}{x} (x > 0)$.

解$\quad (a)y=\begin{cases} x, & x < 0 ,\\ \dfrac{1}{2} , & x=0 \\ 1, & x > 0 .\end{cases}$如图所示.

$(b)y=\displaystyle \lim_{t\to x} \left[ \dfrac{\ln \left( 1+\dfrac{t-x}{x} \right) }{\dfrac{t-x}{x} } \cdot \dfrac{1}{x} \right] =\dfrac{1}{x} $.

$625$.$(a)y=\displaystyle \lim_{n\to \infty } \dfrac{x\tan{}^{2n} \dfrac{\pi x}{4} +\sqrt{x} }{\tan{}^{2n} \dfrac{\pi x}{4} +1} (x\geqslant 0)$；

$(b)y=\displaystyle \lim_{n\to \infty } x\mathrm{sgn} \;\vert \sin{}^2 (n!\pi x)\vert $；

$(c)$作曲线$\displaystyle \lim_{n\to \infty } \sqrt[n]{\vert x\vert^n +\vert y\vert^n } =1$.

解$\quad (a)$

$$y=\begin{cases} \sqrt{x} , & 0\leqslant x < 1,4k-1 < x < 4k+1 ,\\ x , & 4k-3 < x < 4k-2,4k-2 < x < 4k-1, \\ \dfrac{1}{2} (\sqrt{x} +x), & x=2k-1 ,\end{cases}$$

$(k=1,2,3,\cdots )$

1
2
3
4

f[x\_] := Which[x < 1, Sqrt[x], x < 2, x, x < 3, x, x < 5, Sqrt[x], x < 6, x, x < 7, x, x < 9, Sqrt[x]];
p1 = Plot[f[x], {x, 0, 9}];
p2 = ListPlot[{{1, 1}, {3, 1/2 (Sqrt[3] + 3)}, {5, 1/2 (Sqrt[5] + 5)}, {7, 1/2 (Sqrt[7] + 7)}}];
Show[{p1, p2}]

$(b)$

$$y=\begin{cases} 0 , & x为有理数 ,\\ x , & x为无理数 ,\end{cases}$$

$(c)$正方形的闭曲线$\max{\lbrace \vert x\vert ,\vert y\vert \rbrace } =1$.

$626$.若

$$\lim_{x\to \infty } [f(x)-(kx+b)]=0,$$

则直线$y=kx+b$称为曲线$y=f(x)$的（斜）渐近线.利用此方程推出渐近线存在的充分必要条件.

解$\quad $先讨论渐近线从右边伸向无穷远的情形：

$$\lim_{x\to +\infty } [f(x)-(kx+b)]=0.\label{626.1} \tag{1}$$

而在$x > 0$时，

$$\dfrac{f(x)}{x} =\dfrac{f(x)-(kx+b)}{x}+k+\dfrac{b}{x} ,$$

可见

$$\lim_{x\to +\infty } \dfrac{f(x)}{x} =k.\label{626.2} \tag{2}$$

又由$\eqref{626.1}$式得

$$\lim_{x\to +\infty } [f(x)-kx]=b,\label{626.3} \tag{3} $$

即常数$k,b$可由$\eqref{626.2}$、$\eqref{626.3}$式确定.反之，若极限$\displaystyle \lim_{x\to +\infty } \dfrac{f(x)}{x} $存在，且为有限数$k$，极限$\displaystyle \lim_{x\to +\infty } [f(x)-kx]$存在且有限，等于$b$，则$\eqref{626.1}$式成立，即

$$y=kx+b$$

是一条渐近线.用完全类似的方法可以讨论$x\to -\infty $的情形，且得出同样的结论.

综上所述，所求的渐近线存在的充分必要条件为

$$\lim_{x\to \infty } \dfrac{f(x)}{x} =k,\lim_{x\to \infty } [f(x)-kx]=b,$$

此时，$y=kx+b$为曲线$y=f(x)$的（斜）渐近线.

$627$.求下列曲线的渐近线并作其图像：

$(a)y=\dfrac{x^3}{x^2+x-2} $；$(b)y=\sqrt{x^2+x} $；$(c)y=\sqrt[3]{x^2-x^3} $；

$(d)y=\dfrac{xe^x}{e^x -1} $；$(e)y=\ln (1+e^x) $；$(f)y=x+\arccos{\dfrac{1}{x} } $.

解$\quad (a)$因为$\displaystyle \lim_{x\to 1} y=\infty $及$\displaystyle \lim_{x\to -2} y=\infty $，所以直线$x=1$及$x=-2$为曲线的垂直渐近线.其次，因为

$$k=\lim_{x\to \infty } \dfrac{y}{x} =\lim_{x\to \infty } \dfrac{x^2}{x^2+x-2} =1,$$

而

$$b=\lim_{x\to \infty } (y-kx) =\lim_{x\to \infty } \dfrac{-x^2+2x}{x^2+x-2} =-1,$$

所以，$y=x-1$为曲线的水平渐近线.图像如图所示.

$(b)k_1 =\displaystyle \lim_{x\to +\infty } \dfrac{\sqrt{x^2+x}}{x} =1,b_1 =\displaystyle \lim_{x\to +\infty } (\sqrt{x^2+x} -x)=\dfrac{1}{2} ,$

$k_2 =\displaystyle \lim_{x\to -\infty } \dfrac{\sqrt{x^2+x}}{x} =-1,b_2 =\displaystyle \lim_{x\to -\infty } (\sqrt{x^2+x} -x)=-\dfrac{1}{2} ,$

于是，直线$y=x+\dfrac{1}{2} $及$y=-x-\dfrac{1}{2} $为曲线的（斜）渐近线.

曲线$y=\sqrt{x^2+x} $为双曲线$\dfrac{\left( x+\dfrac{1}{2} \right)^2 }{\dfrac{1}{4} } -\dfrac{y^2}{\dfrac{1}{4} } =1$，在$Ox$轴上方的部分.如图所示.

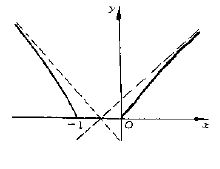
$(c)k=\displaystyle \lim_{x\to \infty } \dfrac{\sqrt[3]{x^2-x^3}}{x} =\lim_{x\to \infty } \sqrt[3]{\dfrac{1}{x} -1} =-1,$

$$\begin{align}
b & =\lim_{x\to \infty } (\sqrt[3]{x^2-x^3} +x)\\
& =\lim_{x\to \infty } \dfrac{x^3+x^2-x^3}{\sqrt[3]{(x^2-x^3)^2} -x\sqrt[3]{x^2-x^3} +x^2} \\
& =\lim_{x\to \infty } \dfrac{1}{\sqrt[3]{\left( \dfrac{1}{x} -1 \right)^2 } -\sqrt[3]{\dfrac{1}{x} -1} +1} \\
& =\dfrac{1}{3} .
\end{align}$$

斜渐近线为

$$y=-x+\dfrac{1}{3} .$$

曲线通过原点及点$A(1,0)$.当$-\infty < x < 1$时，$y > 0$；而当$x > 1$时，$y < 0$.如图所示.

$(d)$当$x > 0$时，

$$k=\lim_{x\to +\infty } \dfrac{xe^x}{x(e^x-1)} =1,$$

$$b=\lim_{x\to +\infty } \left[ \dfrac{xe^x}{e^x -1} -x\right] =\lim_{x\to +\infty } \dfrac{x}{e^x-1} =0,$$

故渐近线为$y=x$；当$x < 0$时

$$k=\lim_{x\to -\infty } \dfrac{xe^x}{x(e^x-1)} =0,b=\lim_{x\to -\infty } \dfrac{xe^x}{e^x-1} =0,$$

故另一渐近线为$y=0$.

曲线在$x=0$处无定义（以后可以说明它是“可去的间断”）.

因为$y > 0$，故图像始终在$Ox$轴上方.如图所示.

$(e)$当$x > 0$时，

$$k=\lim_{x\to +\infty } \dfrac{\ln (1+e^x)}{x} =\lim_{x\to +\infty } \left[ \dfrac{x+\ln (e^{-x} +1)}{x} \right] =1,$$

$$b=\lim_{x\to +\infty } [\ln (1+e^x)-x]=\lim_{x\to +\infty } \ln (e^{-x} +1) =0,$$

故渐近线为$y=x$.同法可求，当$x < 0$时的渐近线为$y=0$.曲线通过点$A(0,\ln 2)$.如图所示.

$(f)k=\displaystyle \lim_{x\to \infty } \dfrac{x+\arccos{\dfrac{1}{x}}}{x} =1,b=\displaystyle [(x+\arccos{\dfrac{1}{x} })-x]=\dfrac{\pi }{2} ,$

故渐近线为$y=x+\dfrac{\pi }{2} $.将函数$y=x$及$y=\arccos{\dfrac{1}{x} }$（见习题$316$）的图像按相加法即得，如图所示.

求下列极限：

$628$.$\displaystyle \lim_{n\to \infty } \left[ \dfrac{x^{n+1}}{(n+1)!} +\dfrac{x^{n+2}}{(n+2)!} +\cdots +\dfrac{x^{2n}}{(2n)!} \right] $.

解$\quad $由于

$$\begin{align}
& \left\vert \dfrac{x^{n+1}}{(n+1)!} +\dfrac{x^{n+2}}{(n+2)!} +\cdots +\dfrac{x^{2n}}{(2n)!} \right\vert \\
\leqslant & \dfrac{\vert x\vert^{n+1}}{(n+1)!} +\dfrac{\vert x\vert^{n+2}}{(n+2)!} +\cdots +\dfrac{\vert x\vert^{2n}}{(2n)!} \\
\leqslant & \dfrac{\vert x\vert^{n+1}}{(n+1)!} (1+\vert x\vert +\cdots +\vert x\vert^{n-1}) .
\end{align}$$

当$\vert x\vert =1$时，上式右端为$\dfrac{n}{(n+1)!} \to 0(n\to \infty )$；

当$\vert x\vert \neq 1$时，此式为

$$\dfrac{\vert x\vert^{n+1}}{(n+1)!} \cdot \dfrac{1-\vert x\vert^n }{1-\vert x\vert} =\dfrac{1}{1-\vert x\vert } \cdot \left[ \dfrac{\vert x\vert^{n+1}}{(n+1)!} -\dfrac{\vert x\vert }{n+1} \cdot \dfrac{(\vert x\vert^2 )^n}{n!} \right] .$$

由习题$61$题的结果知：$\dfrac{\vert x\vert^{n+1}}{(n+1)!}\to 0,\dfrac{(\vert x\vert^2 )^n}{n!} \to 0(n\to \infty )$，故当$n\to \infty $时有$\dfrac{\vert x\vert^{n+1}}{(n+1)!} \cdot \dfrac{1-\vert x\vert^n }{1-\vert x\vert} \to 0$.

于是，对于任意实数$x$，有$\displaystyle \lim_{n\to \infty } \left[ \dfrac{x^{n+1}}{(n+1)!} +\dfrac{x^{n+2}}{(n+2)!} +\cdots +\dfrac{x^{2n}}{(2n)!} \right] =0$.

$629$.$\displaystyle \lim_{n\to \infty } [(1+x)(1+x^2)(1+x^4)\cdots (1+x^{2^n})] (\vert x\vert < 1)$.

解$\quad $因为

$$1+x=\dfrac{1-x^2}{1-x} ,1+x^2=\dfrac{1-x^4}{1-x^2} ,\cdots ,1+x^{2^n} =\dfrac{1-x^{2^{n+1}}}{1-x^{2^n}} .$$

所以，

$$(1+x)(1+x^2)(1+x^4)\cdots (1+x^{2^n})=\dfrac{1-x^{2^{n+1}}}{1-x} .$$

又因$\vert x\vert < 1$，故当$n\to \infty $时，$x^{2^{n+1}} \to 0$.最后得到

$$\lim_{n\to \infty } [(1+x)(1+x^2)(1+x^4)\cdots (1+x^{2^n})] =\dfrac{1}{1-x} .$$

$630$.$\displaystyle \lim_{n\to \infty } \left( \cos{\dfrac{x}{2} } \cos{\dfrac{x}{4} } \cdots \cos{\dfrac{x}{2^n} } \right) $.

解$\quad $因为

$$\begin{align}
& \sin{x} \\
= & 2\cos{\dfrac{x}{2} }\sin{\dfrac{x}{2} } \\
= & 2^2 \cos{\dfrac{x}{2} } \cos{\dfrac{x}{4} }\sin{\dfrac{x}{4} } \\
& \cdots \\
= & 2^n \cos{\dfrac{x}{2} } \cos{\dfrac{x}{4} } \cdots \cos{\dfrac{x}{2^n} } \sin{\dfrac{x}{2^n} } ,
\end{align}$$

所以，

$$\begin{align}
& \lim_{n\to \infty } \left( \cos{\dfrac{x}{2} } \cos{\dfrac{x}{4} } \cdots \cos{\dfrac{x}{2^n} } \right) \\
= & \lim_{n\to \infty } \left( \dfrac{\sin{x} }{2^n} \cdot \dfrac{1}{\sin{\dfrac{x}{2^n} } } \right) \\
= & \lim_{n\to \infty } \left( \dfrac{\sin{x} }{x} \cdot \dfrac{\dfrac{x}{2^n} }{\sin{\dfrac{x}{2^n} } } \right) \\
= & \dfrac{\sin{x} }{x} \quad (x\neq 0).
\end{align}$$

当$x =0$时，原式显然为$1$.

$631$.设

$$\lim_{x\to 0} \dfrac{\varphi (x)}{\psi (x)}=1,$$

其中$\psi (x) > 0$，再设当$n\to \infty $时$\alpha_{mn} \rightrightarrows 0(m=1,2,\cdots ,n)$，换言之，对于任意$\varepsilon > 0$，存在正整数$N(\varepsilon )$，当$m=1,2,\cdots ,n$且$n > N(\varepsilon )$时$0 < \vert \alpha_{mn} \vert < \varepsilon $.证明：

$$\lim_{n\to \infty } [\varphi (\alpha_{1n} )+\varphi (\alpha_{2n} )+\cdots +\varphi (\alpha_{nn} )] =\lim_{n\to \infty } [\psi (\alpha_{1n} ) +\psi (\alpha_{2n} )+\cdots +\psi (\alpha_{nn})],\label{631} \tag{1} $$

此处假定等式$\eqref{631} $右端的极限存在.

证$\quad $根据$\varphi (x)\sim \psi (x)(x\to 0)$，对$\varepsilon > 0$，存在$\delta > 0$，当$0 < \vert x\vert < \delta $时成立

$$\left\vert \dfrac{\varphi (x)}{\psi (x)} -1\right\vert < \varepsilon \Leftrightarrow (1-\varepsilon )\psi (x) < \varphi (x) < (1+\varepsilon ) \psi (x).$$

其中利用了$\psi (x) > 0$的条件.

对于上述$\delta $，根据$\alpha_{mn} \rightrightarrows 0(n\to \infty )$关于$m=1,2,\cdots $一致收敛的条件，存在$N$，当$n > N$时，对一切$m=1,2,\cdots $同时成立$0 < \vert \alpha_{mn} \vert < \delta $，因此也就成立

$$(1-\varepsilon )\psi (\alpha_{mn} ) < \varphi (\alpha_{mn} ) < (1+\varepsilon ) \psi (\alpha_{mn} ).$$

将上述不等式对于$m=1,2,\cdots ,n$求和，得到

$$(1-\varepsilon )\sum_{m=1}^n \psi (\alpha_{mn} ) < \sum_{m=1}^n \varphi (\alpha_{mn} ) < (1+\varepsilon ) \sum_{m=1}^n \psi (\alpha_{mn} ).$$

改写为

$$1-\varepsilon < \dfrac{\displaystyle \sum_{m=1}^n \varphi (\alpha_{mn} )}{\displaystyle \sum_{m=1}^n \psi (\alpha_{mn} )} < 1+\varepsilon .$$

这就已经证明了

$$\lim_{n\to \infty } \dfrac{\displaystyle \sum_{m=1}^n \varphi (\alpha_{mn} )}{\displaystyle \sum_{m=1}^n \psi (\alpha_{mn} )} =1.$$

最后，利用已知极限$\displaystyle \lim_{n\to \infty } \sum_{m+1}^n \psi (\alpha_{mn} )$存在的条件和极限的乘积法则就得到

$$\lim_{n\to \infty } \sum_{m+1}^n \varphi (\alpha_{mn} )=\lim_{n\to \infty } \left( \dfrac{\displaystyle \sum_{m+1}^n \varphi (\alpha_{mn} )}{\displaystyle \sum_{m+1}^n \psi (\alpha_{mn} )} \cdot \sum_{m+1}^n \psi (\alpha_{mn} ) \right) =\lim_{n\to \infty } \sum_{m=1}^n \psi (\alpha_{mn} ).$$

下面的习题$632-636$都是上述定理的应用.我们只讲一个例子.看如何确定该定理中的两个函数和（有双下标的）数列，以及如何验证定理的条件满足.

利用上述定理，求：

$632$.$\displaystyle \lim_{n\to \infty } \sum_{k=1}^n \left( \sqrt[3]{1+\dfrac{k}{n^2} } -1\right) $.

解$\quad $设$x=\dfrac{k}{n^2}$，我们将首先说明它满足习题$631$的条件.首先，

$$\begin{align}
& \lim_{x\to 0 } \dfrac{\sqrt[3]{1+x} -1}{\dfrac{x}{3} } \\
= & \lim_{x\to 0 } \dfrac{\dfrac{x}{\sqrt[3]{(1+x)^2} +\sqrt[3]{1+x} +1} }{\dfrac{x}{3} } \\
= & \lim_{x\to 0 } \dfrac{3}{\sqrt[3]{(1+x)^2} +\sqrt[3]{1+x} +1} \\
= & 1,
\end{align}$$

其次，$\dfrac{k}{n^2} \rightrightarrows 0(n\to \infty ;k=1,2,\cdots ,n)$.最后，$\displaystyle \lim_{n\to \infty } \sum_{k=1}^n \dfrac{k}{3n^2} =\dfrac{1}{6} \displaystyle \lim_{n\to \infty } \dfrac{n(n+1)}{n^2} =\dfrac{1}{6} $.所以，

$$\lim_{n\to \infty } \sum_{k=1}^n \left( \sqrt[3]{1+\dfrac{k}{n^2} } -1\right) =\dfrac{1}{6} .$$

$633$.$\displaystyle \lim_{n\to \infty } \sum_{k=1}^n \left( \sin{\dfrac{ka}{n^2} } \right) $.

解$\quad $因为$\displaystyle \lim_{x\to 0}\dfrac{\sin{x} }{x} =1$，而且当$n\to \infty $时，$\dfrac{ka}{n^2} \rightrightarrows 0(k=1,2,\cdots ,n)$.

又因$\displaystyle \lim_{n\to \infty } \sum_{k=1}^n \dfrac{ka}{n^2} =\dfrac{a}{2} $，故利用习题$631$的结论，即得

$$\lim_{n\to \infty } \sum_{k=1}^n \left( \sin{\dfrac{ka}{n^2} } \right) =\dfrac{a}{2} .$$

$634$.$\displaystyle \lim_{n\to \infty } \sum_{k=1}^n \left( a^{\frac{k}{n^2} } -1\right) (a > 0)$.

解$\quad $我们有$\displaystyle \lim_{x\to 0}\left( \dfrac{a^x-1}{x} \cdot \dfrac{1}{\ln a} \right) =1$，当$n\to \infty $时，$\dfrac{k}{n^2} \cdot \ln a\rightrightarrows 0(k=1,2,\cdots n)$且$\displaystyle \lim_{n\to \infty } \sum_{k=1}^n \dfrac{k}{n^2} \cdot \ln a=\dfrac{1}{2} \ln a$；因而，

$$ \lim_{n\to \infty } \sum_{k=1}^n \left( a^{\frac{k}{n^2} } -1\right) =\dfrac{1}{2} \ln a.$$

$635$.$\displaystyle \lim_{n\to \infty } \prod_{k=1}^n \left( 1+\dfrac{k}{n^2} \right) $.

解$\quad $令$y=\displaystyle \prod_{k=1}^n \left( 1+\dfrac{k}{n^2} \right) $，$\ln y=\displaystyle \sum_{k=1}^n \ln \left( 1+\dfrac{k}{n^2} \right) $.

我们考虑下列极限，

$$\lim_{n\to \infty } \sum_{k=1}^n \ln \left( 1+\dfrac{k}{n^2} \right) .$$

因为$\displaystyle \lim_{n\to \infty } \dfrac{\ln (1+x)}{x} =1$，又$\dfrac{k}{n^2} \rightrightarrows 0(n\to \infty $时，$k=1,2,\cdots n)$，且有$\displaystyle \lim_{n\to \infty } \sum_{k=1}^n \dfrac{k}{n^2} =\dfrac{1}{2} $，所以，$\displaystyle \lim_{n\to \infty } \ln y=\dfrac{1}{2} $，即$\displaystyle \lim_{n\to \infty } \prod_{k=1}^n \left( 1+\dfrac{k}{n^2} \right) =e^{\frac{1}{2} } =\sqrt{e} $.

$636$.$\displaystyle \lim_{n\to \infty } \prod_{k=1}^n \cos{\dfrac{ka}{n\sqrt{n} } } $.

解$\quad $这是$\eqref{8}$型的问题.不妨假设所出现的余弦值都大于$0$，取对数后变为$\eqref{7}$，令$\varphi (x)=\ln \cos{(ax)} $，则有

$$\ln \cos{(ax)} =\ln [1+\cos{(ax)} -1]\sim \cos{(ax)} -1\sim -\dfrac{a^2}{2} x^2 (x\to 0),$$

于是可取$\psi (x)=-\dfrac{a^2}{2} x^2 $，它比函数$\varphi (x)$要简单得多了.

令$\alpha_{kn} =\dfrac{k}{n\sqrt{n} } $，其中$k=1,2,\cdots ,n$，而当$k > n$时令$\alpha_{kn} =0$，则就有$0 < \alpha_{kn} \leqslant \dfrac{1}{\sqrt{n} }$，因此当$n\to \infty $时有$\alpha_{kn} \rightrightarrows 0$，即关于$k=1,2,\cdots $一致收敛于$0$的条件满足.这样就有

$$\lim_{n\to \infty } \sum_{k=1}^n \ln \cos{\dfrac{ka}{n\sqrt{n} } } =-\dfrac{a^2}{2} \lim_{n\to \infty } \sum_{k=1}^n \dfrac{k^2}{n^3} =-\dfrac{a^2}{6} ,$$

其中利用了习题$2$和$53$和结果.由此可见原题的答案为$e^{-\frac{a^2}{6} } $.

注$\quad $习题$631$的定理提供了求$\eqref{7}$和$\eqref{8}$类型的极限的一个很有用的工具.在$\varphi (x)\sim \psi (x)(x\to 0)$中，一般来说是寻找比$\varphi (x)$更简单的$\psi (x)$，但也可能发生相反的情况.这里的关键是用$\psi $代替$\varphi $之后，相应的极限是否求得出.

例如回顾$\S 1.2.3$的最后一题，即习题$147$，要求

$$\lim_{n\to \infty } \left( \dfrac{1}{n+1} +\dfrac{1}{n+2} +\cdots +\dfrac{1}{2n} \right) ,$$

这时在$\eqref{7}$中的$x_{mn} =\dfrac{1}{n+m} $，利用$x\sim \ln (1+x)(x\to 0)$，取$\varphi (x)=x$，$\psi (x)=\ln (1+x)$，$\alpha_{kn} =\dfrac{1}{n+k} $，$k=1,2,\cdots ,n$，则上述极限就可用习题$631$的定理计算如下：

$$\begin{align}
& \lim_{n\to \infty } \left( \dfrac{1}{n+1} +\dfrac{1}{n+2} +\cdots +\dfrac{1}{2n} \right) \\
= & \lim_{n\to \infty } \sum_{k=1}^n \ln \left( 1+\dfrac{1}{n+k} \right) \\
= & \lim_{n\to \infty } \ln \left( \dfrac{n+2}{n+1} \cdot \dfrac{n+3}{n+2} \cdot \cdots \cdot \dfrac{2n+1}{2n} \right) \\
= & \lim_{n\to \infty } \ln \dfrac{2n+1}{n+1} \\
= & \ln 2.
\end{align}$$

学过积分学的读者都知道，还可以用定积分方法求出包括习题$147$在内的许多极限计算问题.见《习题集》后面$\S 4.2$的习题$2219-2230$等，其中的习题$2219$就是习题$147$.此外，还可以补充一点，即有时还需要将习题$631$中的定理和定积分方法联合使用来解决某些稍难一点的问题.所有这些内容都将在《指引》的第二册中学习.

$641$.若$\omega_{h} (f)$为函数$f(x) $在区间$\vert x-\xi \vert \leqslant h(h > 0) $上的振幅，则数

$$\omega_0 (f)=\lim_{h\to 0} \omega_h (f)$$

称为函数$f(x)$在$\xi $点的振幅.

若$f(x)=0$，而在$x\neq 0$时$f(x)$为下列函数，求$f(x)$在点$x=0$的振幅：

$(a)f(x)=\sin{\dfrac{1}{x} } $；$(b)f(x)=\dfrac{1}{x^2} \cos{}^2 \dfrac{1}{x} $；

$(c)f(x)=x\left( 2+\sin{\dfrac{1}{x}} \right) $；$(d)f(x)=\dfrac{1}{\pi } \arctan{\dfrac{1}{x} } $；

$(e)f(x)=\dfrac{\vert \sin{x} \vert }{x} $；$(f)f(x)=\dfrac{1}{1+e^{\frac{1}{x} }} $；

$(g)f(x)=(1+\vert x\vert )^{\frac{1}{x} } $.

解$\quad (a)\omega_h (f)=2,\omega_0 (f)=2$；

$(b)\omega_h (f)=+\infty ,\omega_0 (f)=+\infty $；

$(c)\omega_h (f)=3h-h=2h,\omega_0 (f)=0 $；

$(d)\omega_h (f)=\dfrac{1}{\pi } \left[ \arctan{\dfrac{1}{h} } -\arctan{\dfrac{1}{(-h)} } \right] ,\omega_0 (f)=\dfrac{2}{\pi } \cdot \dfrac{\pi }{2} =1$；

$(e)\omega_h (f)=2,\omega_0 (f)=2 $；

$(f)\omega_h (f)=\left\vert \dfrac{1}{1+e^{\frac{1}{h} }} - \dfrac{1}{1+e^{-\frac{1}{h} }}\right\vert ,\omega_0 (f)=1 $；

$(e)\omega_h (f)=(1+h)^{\frac{1}{h} }-(1+h)^{-\frac{1}{h} },\omega_0 (f)=e-e^{-1}=2\sinh{1} $；

$642$.设

$$f(x)=\sin{\dfrac{1}{x} } ,$$

证明：对于满足条件$-1 \leqslant \alpha \leqslant 1$的任何数$\alpha $，可以选出数列$x_n \to 0(n=1,2,\cdots )$，使得

$$\lim_{n\to \infty } f(x_n )=\alpha .$$

证$\quad $对于确定的$\alpha \colon \vert \alpha \vert \leqslant 1$，总存在$x_0 \in \left[ -\dfrac{\pi }{2} ,\dfrac{\pi }{2} \right]$，使$\sin{x_0 } =\alpha $.

令$x_n =\dfrac{1}{2n\pi +x_0 } $，则显然有$\displaystyle \lim_{n\to \infty } x_n =0$.又因

$$f(x_n )=\sin{\dfrac{1}{x_n } } =\sin{(2n\pi +x_0 )} =\alpha ,$$

所以，$\displaystyle \lim_{n\to \infty } f(x_n )=\alpha $.

$643$.求$\displaystyle l=\varliminf_{x\to 0} f(x)$和$\displaystyle L=\varlimsup_{x\to 0} f(x)$：

$(a)f(x)=\sin{}^2 \dfrac{1}{x} +\dfrac{2}{\pi } \arctan{\dfrac{1}{x} } $；$(b)f(x)=(2-x^2)\cos{\dfrac{1}{x} } $；

$(c)f(x)=\left( 1+\cos{}^2 \dfrac{1}{x} \right)^{\sec{}^2 \frac{1}{x} } $.

解$\quad $由$l$及$L$的定义，容易求得

$(a)l=-1,L=2$；

$(b)l=-2,L=2$；

$(c)l=2,L=e$；

$644$.求$\displaystyle l=\varliminf_{x\to \infty } f(x)$和$\displaystyle L=\varlimsup_{x\to \infty } f(x)$：

$(a)f(x)=\sin{x} $；$(b)f(x)=x^2 \cos{}^2 x$；

$(c)f(x)=2^{\sin{x^2} } $；$(d)f(x)=\dfrac{x}{1+x^2\sin{}^2 x} (x\geqslant 0) $.

解$\quad $由$l$及$L$的定义，容易求得

$(a)l=-1,L=1$；

$(b)l=0,L=+\infty $；

$(c)l=\dfrac{1}{2} ,L=2$；

$(d)l=0,L=+\infty $.

补注

在这个补注中有以下内容：

$1$.对于等价代换法作补充说明；

$2$.结合习题$607$给出复合函数极限计算的充分条件；

$3$.推广的柯西命题（习题$608-610$）;

$4$.函数$e^x$的两种表示（习题$611-612$）;

$5$.迭代生成的函数列（习题$606$，$637-640$）.

关于等价量代换法的补充说明

如前面的大量习题所表明，等价概念和等价量代换法在本节的函数极限计算中起重要作用.下面是几点补充说明.

为简明起见，用$\lim $表示某个极限过程，其中包括数列极限在内，$u$和$v$是两个函数，其中$v\neq 0$.若有

$$\lim \dfrac{u}{v} =1,$$

则称$u$和$v$对于$\lim $所指的极限过程为等价，简记为$u\sim v$.

上述等式可改写为

$$\lim \dfrac{u-v}{v} =0,$$

从而也可以用小$o$记号定为

$$u=v(1+o(1))=v+o(v).$$

由于这个记法中不需要$v\neq 0$的条件，因此往往作为$u\sim v$的更广一些的含义.

对于具体的等价关系，由于存在多种函数极限，因此必须写明等价关系是对什么样的函数极限而说的，即在后面添上$(x\to a)$.只有在数列极限的情况，习惯上往往可以省去$(n\to \infty )$.

例如对于函数$\ln x$，以下两个等价关系都是正确的，这时后面括号内的说明是不可缺少的：

$$\ln (1+x)\sim x(x\to 0),\ln x\sim x-1(x\to 1).$$

又如对于函数$x^3+x$有以下等价关系：

$$x^3+x\sim x^3 (x\to +\infty ),x^3+x\sim x(x\to 0),$$

两者的意义完全不同.

这里要说明，虽然在本节中$u\sim v$一般都用于无穷小量之间的等价，但从等价记号的定义来看，$u\sim v$中并没有说在指定的极限过程中$u$和$v$是否是无穷小量或无穷大量，或是其他情况.如上面$x^3+x$的第一个等价关系就是指两个无穷大量之间的等价.

下面说一下等价量代换法.这就是在$u\sim \tilde{u}$时，就可推出有

$$uv\sim \tilde{u} v,\dfrac{u}{v} \sim \dfrac{\tilde{u} }{v} (v\neq 0),\dfrac{v}{u} \sim \dfrac{v}{\tilde{u} } (n\neq 0).$$

因此在求乘除形式的极限时，可以将其中的因子换为等价量来计算，本节的许多题中都是如此.举个简单例子.由于$\sin{x} \sim x(x\to 0)$，$\ln (1+x)\sim x(x\to 0)$，因此就有

$$\lim_{x\to 0} \dfrac{\sin{3x}}{\ln (1-x)} =\lim_{x\to 0} \dfrac{3x}{-x} =-3.$$

显然这只不过是将

$$\lim_{x\to 0} \dfrac{\sin{3x}}{\ln (1-x)} =\lim_{x\to 0} \left( \dfrac{\sin{3x}}{3x} \cdot \dfrac{-x}{\ln (1-x)} \cdot \dfrac{3x}{-x} \right) =\lim_{x\to 0} \dfrac{3x}{-x} =-3$$

写得更简单一点而已.

最后要指出，对等价量代换法使用不当是初学者容易犯的一种错误.举个最简单的例子.例如前面已经有$x^3+x\sim x(x\to 0)$，如果在极限计算

$$\lim_{x\to 0} \dfrac{(x^3+x)-x}{x^3} =1$$

中将分子的$(x^3+x)$用等价量$x$来代替，则得到的结果就是$0$了.当然读者会认为谁也不会犯这样的“低级”错误.但实际上发生的错误与这个简单例子在本质上是一样的.从无穷小量的阶数很容易理解这类错误的原因.在上面的例子中分母对于$x\to 0$而言是三阶无穷小量，而分子的两项，即$(x^3+x)$和$x$都是一阶无穷小量，关键在于它们的差是三阶无穷小量.上面的错误做法就是用$x$代替$x^3+x$，抛弃了将要起关键作用的$x^3$项.打个比方，这与计算

$$\dfrac{1.001-1}{0.001} =1$$

时不能将左边分子的第一项用$1$代替是一个道理.

下面举一个在一次考试中出现的错误，即要求极限

$$I=\lim_{x\to 0} \dfrac{\dfrac{x}{1+x} -\ln (1+x)}{x^2} .$$

当时的学生已经学过泰勒公式和洛必达法则，但还是有不少学生用等价量代换法做.

第一种错误是对于分子的两项分别利用$\dfrac{x}{1+x} \sim x(x\to 0)$和$\ln (1+x)\sim x(x\to 0)$换为等价量$x$，于是分子成为$x-x=0$，所以$I=0$.

第二种错误是利用$\dfrac{x}{1+x} \sim x(x\to 0)$，将分子的第一项换为它的等价量$x$，对第二项则用泰勒公式，于是有

$$I=\lim_{x\to 0} \dfrac{x-\ln (1+x)}{x^2} =\lim_{x\to 0} \dfrac{x-(x-\dfrac{x^2}{2} +o(x^2))}{x^2} =\dfrac{1}{2} .$$

第三种错误是在分子中用$\ln (1+x)\sim x(x\to 0)$将第二项换为$x$，于是

$$I=\lim_{x\to 0} \dfrac{\dfrac{x}{1+x} -x}{x^2} =\lim_{x\to 0} \dfrac{x-x(1+x)}{x^2(1+x)} =\lim_{x\to 0} \dfrac{-x^2}{x^2+x^3} =-1.$$

以上三个答案都是错的，正确的答案是$-\dfrac{1}{2}$.错误的根源相同，都是不恰当地应用等价量代换法.其实只要从无穷小量的阶数来观察问题就很容易明白这里的困难.将$x\to 0$时的$x$作为一阶无穷小量，则本题中的分母就是二阶无穷小量.由于分子中的两项的一阶都是$x$，恰如抵消，因此应当将分子的每一项都写出到$x^2$项才行.

虽然本书目前还没有进入到微分学，但还是可以得到

$$\lim_{x\to 0} \dfrac{\dfrac{x}{1+x} -x}{x^2} =\lim_{x\to 0} \dfrac{x-(1+x)x}{x^2(1+x)} =-1,$$

若利用习题$611(b)$则还可以得到

$$\lim_{x\to 0} \dfrac{x-\ln (1+x)}{x^2} =\dfrac{1}{2} .$$

合并这两个结果就得到

$$\lim_{x\to 0} \dfrac{\left( \dfrac{x}{1+x} -x\right) +\left( x-\ln (1+x)\right) }{x^2} =-1+\dfrac{1}{2} =-\dfrac{1}{2} .$$

小结$\quad $等价量代换法就是在乘除形式的极限计算中将其中的因子用等价量代替以简化计算.但是在求和的表达式中，不能随意将其中的一项或几项用等价量来代替.

关于复合函数的极限问题

在本节的函数极限计算中广泛利用了复合函数运算来计算一些比较复杂的极限问题.习题$607$指出这种做法不是无条件成立的.这里我们先回答该习题提出的问题，然后对于习题$607$中的正面结论给出一些充分条件.

$607$.设$\displaystyle \lim_{x\to a} \varphi (x)=A$及$\displaystyle \lim_{x\to A} \psi (x)=B$，由此可否推出

$$\lim_{x\to a} \psi (\varphi (x)) =B?$$

研究例子：

$$\varphi (x)=\begin{cases} \dfrac{1}{q} , & x=\dfrac{p}{q} (p,q是互素的整数,q > 0),\\ 0, & x为无理数, \end{cases} \quad \psi (x)=\begin{cases} 1, & x\neq 0 ,\\ 0, & x=0 ,\end{cases} $$

并且$x\to 0$.

解$\quad $本题已经对于所提的问题给出反例，因此只要验证即可.

函数$\varphi (x)$即是著名的黎曼函数.对于它的较详细的讨论见$\S 1.7.3$的习题$736$.其中包含了本题中需要的$\displaystyle \lim_{x\to 0} \varphi (x) =0$，这里不另行证明.

这时$a=0,A=0$.此外，由$A=0$就得到$B=\displaystyle \lim_{x\to A} \psi (x)=1$.

然而复合函数$\psi (\varphi (x))$当$x\neq 0$时有两种可能性.若$x$为无理数，则$\varphi (x) =0$，因此$\psi (\varphi (x)) =\psi (0)=0$；若$x$为有理数，则$\varphi (x)\neq 0$，因此$\psi (\varphi (x))=1$.这表明复合函数$\psi (\varphi (x))$在点$x=0$的任意邻近可以取到$0$，也可以取到$1$，因此当$x\to 0$时函数$\psi (\varphi (x))$的极限不存在.

在前面已经遇到过许多例子，它们表明在习题的条件下结论$\displaystyle \lim_{x\to a} \psi (\varphi (x))=B$经常成立，但目前却有一个例子表明这个结论也可以不成立，因此答案是：不一定成立.

下面讲两个问题.第一，为什么会发生上述现象？第二，什么条件下习题中的$\displaystyle \lim_{x\to a} \psi (\varphi (x))=\lim_{x\to A} \psi (x)=B$能够成立？

第一个问题从函数极限定义就可以得到解释.

考察习题$607$中给出的例子中$\psi (0)=0$，而这与$\displaystyle \lim_{y\to 0} \psi (y)=1$毫无关系.

然而在考虑复合函数$\psi (\varphi (x))$在$x\to a$的极限时，其中的$\varphi (x)$完全可能取到$A$，甚至会在$x\to a$的过程中无限多次取到$A$.这就是问题所在.若$\psi (y)$于$y=A$处无定义，则$\displaystyle \lim_{x\to a} \psi (\varphi (x))$无意义；若$\psi (y)$于$y=A$处有定义，则习题$607$的例子告诉我们$\displaystyle \lim_{x\to a} \psi (\varphi (x))$未必等于$B=\displaystyle \lim_{y\to A} \psi (y)$.

下面讲第二个问题，即在什么条件下会成立以下关系：

$$\lim_{x\to a} \varphi (x)=A,\lim_{x\to A} \psi (x)=B\Rightarrow \lim_{x\to a} \psi (\varphi (x))=B.\label{9} \tag{1.41}$$

从前面对于第一个问题的分析可以知道，在以下几个条件下$\eqref{9}$都能够成立.

$(1)\psi (A)=B$，即函数$\psi $在点$A$处连续；

$(2)$存在某个$\delta_0 > 0$，使得在$0 < \vert x-a\vert < \delta_0 $时$\psi (x)\neq A$；

$(3)A=\pm \infty$，而$\displaystyle \lim_{x\to A} \psi (x)$有意义.

解释$\quad $条件$(1)$使得在$\displaystyle \lim_{x\to A} \psi (x)=B$中允许$x$取到$A$；条件$(2)$使得在$x\to a$时复合函数$\psi (\varphi (x))$中的内层$\varphi (x)$不会取到$A$；条件$(3)$与$(2)$类似，因为$\varphi (x)$一定是有限实数，因此不可能取到$\pm \infty $.

读者如果有兴趣，可以检查前面用到复合函数极限的一些实际例子，看看是否满足以上的条件.（典型的例子就是从$\eqref{2}$）推出$\eqref{3} -\eqref{5} $.）

柯西命题的推广

这是将数列极限中的柯西命题和施托尔茨定理（即习题$138-141,143$等）从离散推广到连续.在学习上述数列极限习题的基础上，就不难解决这里的习题.下面给出前题的解答供参考，其中的方法与习题$138-139$相同.

$608$.证明柯西定理：若函数$f(x)$定义于区间$(a,+\infty )$，并且在每一个有限区间$(a,b)$内是有界的，则

$$(a)\lim_{x\to +\infty } \dfrac{f(x)}{x} =\lim_{x\to +\infty } [f(x+1)-f(x)];$$

$$(b)\lim_{x\to +\infty } [f(x)]^{\frac{1}{x} } =\lim_{x\to +\infty } \dfrac{f(x+1)}{f(x)} (f(x)\geqslant C > 0),$$

假定等式右端的极限都存在.

证$\quad (a)$设$\displaystyle \lim_{x\to +\infty } [f(x+1)-f(x)]=A$，则容易发现只要对$A=0$的情况作出证明就足够了，因为当$A\neq 0$时可以用辅助函数$f(x)-Ax$来代替$f(x)$.此外又不妨设已有$a > 0$.

对给定的任意$\varepsilon > 0$，存在$M_1 > a$，当$x\geqslant M_1 $时成立$\vert f(x+1)-f(x)\vert < \dfrac{1}{2} \varepsilon $.

对$x > M_1 $，取正整数$n=[x-M_1 +1]$，则有$n\leqslant x-M_1 +1 < n+1$，也就是

$$M_1 \leqslant x-n+1 < M_1 +1.$$

现在对于$x > M_1 $时的分式$\dfrac{f(x)}{x} $的分子做分拆并估计如下：

$$\begin{align}
& \left\vert \dfrac{f(x)}{x} \right\vert \\
\leqslant & \dfrac{\vert f(x)-f(x-1)\vert +\cdots +\vert f(x-n+2)-f(x-n+1)\vert +\vert f(x-n+1)\vert }{x} \\
\leqslant & \dfrac{n-1}{x} \cdot \dfrac{\varepsilon }{2} +\dfrac{\vert f(x-n+1)\vert }{x} \\
< & \dfrac{\varepsilon }{2} +\dfrac{\vert f(x-n+1)\vert }{x} .
\end{align}$$

由于最后一项的分子中的自变量$x-n+1\in [M_1 ,M_1 +1)$，而$f$在任意有限区间上有界，因此存在$M > M_1 $，使得当$x > M$时有$\dfrac{\vert f(x-n+1)\vert }{x} < \dfrac{\varepsilon }{2} $，于是也同时成立了$\left\vert \dfrac{f(x)}{x} \right\vert < \varepsilon $.

$(b)$由已经证明的$(a)$和指数函数与对数函数的连续性就有

$$\begin{align}
& \lim_{x\to +\infty } [f(x)]^{\frac{1}{x} } \\
= & \lim_{x\to +\infty } e^{\frac{\ln f(x)}{x} } \\
= & e^{\lim\limits_{x\to +\infty } \frac{\ln f(x)}{x} } \\
= & e^{\lim\limits_{x\to +\infty } (\ln f(x+1)-\ln f(x)) } \\
= & e^{\ln \left( \lim\limits_{x\to +\infty } \frac{f(x+1)}{f(x)} \right) } \\
= & \lim_{x\to +\infty } \dfrac{f(x+1)}{f(x)} .
\end{align}$$

$609$.证明：若$(1)$函数$f(x)$定义于区域$x > a$；$(2)f(x)$在每一个有限区域$a < x < b$内是有界的；$(3)\displaystyle \lim_{x\to +\infty } [f(x+1)-f(x)]=\pm \infty $，则

$$\lim_{x\to +\infty } \dfrac{f(x)}{x} =\pm \infty .$$

证$\quad $不妨设有$a > 0$.先讨论条件$(3)$为$+\infty $的情况.

对给定的任意$K > 0$，存在$M_1 > a$，当$x\geqslant M_1 $时成立$f(x+1)-f(x) > 2K$，对$x > M_1 $，取正整数$n=[x-M_1 +1]$，则有$n \leqslant x-M_1 +1 < n+1$，也就是

$$M_1 \leqslant x-n+1 < M_1 +1.$$

现在对于$x > M_1 $时的分式$\dfrac{f(x)}{x}$的分子做分拆并估计如下：

$$\begin{align}
& \left\vert \dfrac{f(x)}{x} \right\vert \\
= & \dfrac{[ f(x)-f(x-1)] +\cdots +[ f(x-n+2)-f(x-n+1)] + f(x-n+1)}{x} \\
\geqslant & \dfrac{n-1}{x} \cdot 2K -\dfrac{\vert f(x-n+1)\vert }{x} .
\end{align}$$

这时有$\dfrac{n-1}{x} > 1-\dfrac{M_1 +1}{x} $，又由于上式的最后一项的分子中的自变量$x-n+1\in [M_1 ,M_1 +1)$，而$f$在任意有限区间上有界，因此存在$M > M_1 $，使得当$x > M$时有$\dfrac{\vert f(x-n+1)\vert }{x} < \dfrac{K}{3} $，且同时成立$\dfrac{n-1}{x} > \dfrac{2}{3} $，于是当$x > M$时就得到

$$\dfrac{f(x)}{x} > \dfrac{2}{3} \cdot 2K -\dfrac{K}{3} =K,$$

这样就证明了$\displaystyle \lim_{x\to +\infty } \dfrac{f(x)}{x} =+\infty $.

对于条件$(3)$为$-\infty $的情况，或者模仿上面的方法，或者令$g(x)=-f(x)$，就可以归结为已经证明的结论.从略.

习题$610$及其证明都没有新的内容，从略.读者可以试试看，能否证明它，用以测试自己是否已经掌握了前面的方法.

$610$.证明：若$(1)$函数$f(x)$定义于区域$x > a$；$(2)f(x)$在每一个有限区域$a < x < b$内是有界的；$(3)$对于某正整数$n$，存在有限的或无穷的极限

$$\lim_{x\to +\infty } \dfrac{f(x+1)-f(x)}{x^n} =l;$$

则

$$\lim_{x\to +\infty } \dfrac{f(x)}{x^{n+1}} =\dfrac{l}{n+1} .$$

证$\quad $先证一条一般性的定理（Stolz定理在函数情形的推广）：若$(1)$函数$f(x)$与$g(x)$都定义于区域$x > a$内；$(2)f(x)$与$g(x)$在每一个有限区域$a < x < b$内有界，并且$g(x)$当$x > a$时满足$g(x+1) > g(x)$且$\displaystyle \lim_{x\to +\infty } g(x)=+\infty $；$(3)$存在极限

$$\lim_{x\to +\infty } \dfrac{f(x+1)-f(x)}{g(x+1)-g(x)} =l$$

（$l$为有限数或为$+\infty $或为$-\infty $）;则必$\displaystyle \lim_{x\to +\infty } \dfrac{f(x)}{g(x)} =l$.

证如下：

先证$l$为有限数.任给$\varepsilon > 0$，存在正数$X_0 > a$，使当$x\geqslant X_0 $时，恒有

$$\left\vert \dfrac{f(x+1)-f(x)}{g(x+1)-g(x)} -l\right\vert < \dfrac{\varepsilon }{2} .$$

现设$x > X_0 +1$.于是，恰有一个正整数$n$（依赖于$x$），使$n\leqslant x-X_0 < n+1$.令$\tau =x-X_0 -n $，则$0\leqslant \tau < 1$，$x=X_0 +\tau +n $. 我们有

$$\begin{align}
& \dfrac{f(x)-f(X_0 +\tau )}{g(x)-g(X_0 +\tau )} -l \\
= & \sum_{k=1}^n \dfrac{g(X_0 +\tau +k)-g(X_0 +\tau +k-1)}{g(x)-g(X_0 +\tau )} \cdot \left[ \dfrac{f(X_0 +\tau +k)-f(X_0 +\tau +k-1)}{g(X_0 +\tau +k)-g(X_0 +\tau +k-1)} -l\right] , \end{align}$$

而

$$\left\vert \dfrac{f(X_0 +\tau +k)-f(X_0 +\tau +k-1)}{g(X_0 +\tau +k)-g(X_0 +\tau +k-1)} -l\right\vert < \dfrac{\varepsilon }{2} (k=1,2,\cdots ,n),$$

又由于

$$\begin{align}
& g(x) \\
= & g(X_0 +\tau +n) \\
{>} & g(X_0 +\tau +n -1) \\
{>} & g(X_0 +\tau +n -2) \\
{>} & \cdots \\
{>} & g(X_0 +\tau ) ,
\end{align}$$

从而，

$$\dfrac{g(X_0 +\tau +k)-g(X_0 +\tau +k-1)}{g(x)-g(X_0 +\tau )} > 0(k=1,2,\cdots ,n);$$

由此可知

$$\begin{align}
& \left\vert \dfrac{f(x)-f(X_0 +\tau )}{g(x)-g(X_0 +\tau )} -l \right\vert \\
{<} & \dfrac{\varepsilon }{2} \sum_{k=1}^n \dfrac{g(X_0 +\tau +k)-g(X_0 +\tau +k-1)}{g(x)-g(X_0 +\tau )} \\
= & \dfrac{\varepsilon }{2} .
\end{align}$$

容易直接验证等式

$$\begin{align}
& \dfrac{f(x)}{g(x)} -l \\
= & \left[ 1-\dfrac{g(X_0 +\tau )}{g(x)} \right] \cdot \left[ \dfrac{f(x)-f(X_0 +\tau )}{g(x)-g(X_0 +\tau )} -l\right] +\dfrac{f(X_0 +\tau )-lg(X_0 +\tau )}{g(x)} .
\end{align}$$

由于$\displaystyle \lim_{x\to +\infty } g(x)=+\infty $，并且$f(x)$与$g(x)$都在$X_0 \leqslant x < X_0 +1$上有界，故必有正数$X_1 > a$存在，使当$x > X_1 $时，恒有

$$\left\vert \dfrac{g(X_0 +\tau )}{g(x)} \right\vert < \dfrac{1}{2} ,\left\vert \dfrac{f(X_0 +\tau )-lg(X_0 +\tau )}{g(x)} \right\vert < \dfrac{\varepsilon }{4} .$$

令$X=\max{\lbrace X_0 +1 ,X_1 \rbrace }$.于是，当$x > X$时，恒有

$$\left\vert \dfrac{f(x)}{g(x)} -l\right\vert < \dfrac{3}{2} \cdot \dfrac{\varepsilon }{2} + \dfrac{\varepsilon }{4} =\varepsilon .$$

由此可知$\displaystyle \lim_{x\to +\infty } \dfrac{f(x)}{g(x)} =l$，$l$为有限数获证.

下设$l=+\infty $（若$l=-\infty $，则考虑函数$-f(x)$即可化为$l=+\infty $的情形）.任给$G > 0$，存在正数$X_0 > a$，使当$x\geqslant X_0 $时，恒有

$$\dfrac{f(x+1)-f(x)}{g(x+1)-g(x)} > 4G.$$

当$x > X_0 +1 $时，仿前一段之证，有

$$\begin{align}
& \dfrac{f(x)-f(X_0 +\tau )}{g(x)-g(X_0 +\tau )} \\
= & \sum_{k=1}^n \dfrac{g(X_0 +\tau +k)-g(X_0 +\tau +k-1)}{g(x)-g(X_0 +\tau )} \cdot \dfrac{f(X_0 +\tau +k)-f(X_0 +\tau +k-1)}{g(X_0 +\tau +k)-g(X_0 +\tau +k-1)} \end{align}$$

从而，

$$\dfrac{f(x)-f(X_0 +\tau )}{g(x)-g(X_0 +\tau )} > 4G \sum_{k=1}^n \dfrac{g(X_0 +\tau +k)-g(X_0 +\tau +k-1)}{g(x)-g(X_0 +\tau )} =4G.$$

易知

$$\dfrac{f(x)}{g(x)} =\left[ 1-\dfrac{g(X_0 +\tau )}{g(x)} \right] \cdot \dfrac{f(x)-f(X_0 +\tau )}{g(x)-g(X_0 +\tau )} +\dfrac{f(X_0 +\tau )}{g(x)} .$$

根据$\displaystyle \lim_{x\to +\infty } g(x)=+\infty $以及$f(x)$，$g(x)$在$X_0 \leqslant x < X_0 +1$上的有界性，可取正数$X_1 > a$，使当$x > X_1 $时，恒有

$$\left\vert \dfrac{g(X_0 +\tau )}{g(x)} \right\vert < \dfrac{1}{2} ,\left\vert \dfrac{f(X_0 +\tau )}{g(x)} \right\vert < G.$$

令$X=\max{\lbrace X_0 +1 ,X_1 \rbrace }$.于是，当$x > X$时，恒有

$$\dfrac{f(x)}{g(x)} > \dfrac{1}{2} \cdot 4G -G=G .$$

由此可知$\displaystyle \lim_{x\to +\infty } \dfrac{f(x)}{g(x)} =+\infty $.所述一般性定理获证.

现在我们应用此一般定理来证明本题，在一般性定理中取$g(x)=x^{n+1} $.显然此$g(x)$满足一般性定理的条件，并且

$$\begin{align}
& \lim_{x\to +\infty } \dfrac{f(x+1)-f(x)}{g(x+1)-g(x)} \\
= & \lim_{x\to +\infty } \dfrac{f(x+1)-f(x)}{(x+1)^{n+1}-x^{n+1}} \\
= & \lim_{x\to +\infty } \dfrac{f(x+1)-f(x)}{(n+1)x^n +\dfrac{1}{2} (n+1)nx^{n-1} +\cdots +(n+1)x+1} \\
= & \lim_{x\to +\infty } \left[ \dfrac{f(x+1)-f(x)}{x^n} \cdot \dfrac{1}{(n+1)+\cdots +(n+1)x^{-n+1}+x^{-n}} \right] \\
= & \dfrac{l}{n+1} .
\end{align}$$

由此，根据此一般性定理，即得$\displaystyle \lim_{x\to +\infty } \dfrac{f(x)}{x^{n+1}} =\lim_{x\to +\infty } \dfrac{f(x)}{g(x)} =\dfrac{l}{n+1} $.

函数$e^x$的两种表示

习题$611$将习题$69$和$72$的内容从数列推广到函数序列.

$611$.证明：

$(a)\displaystyle \lim_{n\to \infty } \left( 1+\dfrac{x}{n} \right)^n =e^x $；

$(b)\displaystyle \lim_{n\to \infty } \left( 1+x+\dfrac{x^2}{2!} +\cdots +\dfrac{x^n}{n!} \right) =e^x $.

证$\quad (a)$用习题$71$和代入法即有

$$\lim_{n\to \infty } \left( 1+\dfrac{x}{n} \right)^n =\lim_{n\to \infty } \left[ \left( 1+\dfrac{x}{n} \right)^{\frac{n}{x} } \right]^x =e^x .$$

$(b)$仿照习题$72$的解，引入记号：$y_n (x)=\left( 1+\dfrac{x}{n} \right)^n $，$z_n (x)=1+x+\dfrac{x^2}{2!} +\cdots +\dfrac{x^n}{n!} $，$n=1,2,\cdots $，它们是两个函数序列.

首先证明$\lbrace z_n (x)\rbrace $对任何$x$值都是收敛的.

用柯西收敛准则，对于任何正整数$n$和$p$，有

$$\begin{align}
& \vert z_{n+p} (x)-z_n (x)\vert \\
= & \left\vert \dfrac{x^{n+1}}{(n+1)!} +\dfrac{x^{n+2}}{(n+2)!} +\cdots +\dfrac{x^{n+p}}{(n+p)!} \right\vert \\
\leqslant & \dfrac{\vert x\vert^{n+1}}{(n+1)!} +\dfrac{\vert x\vert^{n+2}}{(n+2)!} +\cdots +\dfrac{\vert x\vert^{n+p}}{(n+p)!} \\
= & \dfrac{\vert x\vert^{n+1}}{(n+1)!} \left( 1+\dfrac{\vert x\vert }{(n+2)} +\cdots +\dfrac{\vert x\vert^{p-1}}{(n+2)\cdots (n+p)} \right) \\
\leqslant & \dfrac{\vert x\vert^{n+1}}{(n+1)!} \left( 1+\dfrac{\vert x\vert }{(n+2)} +\cdots +\dfrac{\vert x\vert^{p-1}}{(n+2)^{p-1}} \right) \\
\leqslant & \dfrac{\vert x\vert^{n+1}}{(n+1)!} \cdot \dfrac{1}{1-\dfrac{\vert x\vert }{n+2} } \\
= & \dfrac{\vert x\vert^{n+1}}{(n+1)!} \cdot \dfrac{n+2}{n+2-\vert x\vert } ,
\end{align}$$

其中假设已取$n$充分大，使得$n+2 > \vert x\vert $.

由于当$n\to \infty $时上述最后一式极限为$0$（即习题$61$的$\displaystyle \lim_{n\to \infty } \dfrac{a^n}{n!}=0$），因此对给定的任意正数$\varepsilon > 0$，存在$N$，当$n > N$且$p$为任意正整数时，上述最后一式小于$\varepsilon $.这就证明了对每一个$x$，存在极限$\displaystyle \lim_{n\to \infty } z_n (x)=E(x)$.

下面将证明$E(x)=e^x $，其中的方法与$\S 1.2.3$的习题$72$中的方法几乎完全相同.

直接估计函数序列$\lbrace y_n (x)\rbrace $和$\lbrace z_n (x)\rbrace $之差.将$y_n (x)=\left( 1+\dfrac{x}{n}\right)^n $用二项式定理展开，其中前两项$1+x$与$z_n (x)$的前两项相同，因而抵消，然后与习题$72$类似地利用习题$6$的伯努利不等式，就有

$$\begin{align}
& \vert z_n (x)-y_n (x)\vert \\
= & \left\vert \sum_{k=2}^n \dfrac{x^k}{k!} -\sum_{k=2}^n \dfrac{x^k}{k!} \left( 1-\dfrac{1}{n} \right) \cdots \left( 1-\dfrac{k-1}{n} \right) \right\vert \\
\leqslant & \sum_{k=2}^n \dfrac{\vert x\vert^k}{k!} \left[ 1-\left( 1-\dfrac{1}{n} \right) \cdots \left( 1-\dfrac{k-1}{n} \right) \right] \\
\leqslant & \sum_{k=2}^n \dfrac{\vert x\vert^k}{k!} \left[ 1-\left( 1-\dfrac{(k-1)k}{2n} \right) \right] \\
= & \dfrac{1}{2n} \sum_{k=2}^n \dfrac{\vert x\vert^k }{(k-2)!} \\
\leqslant & \dfrac{x^2}{2n} \cdot E(\vert x\vert ),
\end{align}$$

可见有$\displaystyle \lim_{n\to \infty } \vert z_n (x)-y_n (x)\vert =0$.这就证明了函数序列$\lbrace y_n (x)\rbrace $和$\lbrace z_n (x)\rbrace $具有相同的极限，即$E(x)=e^x $.

$612$.证明：

$$\lim_{n\to \infty } n\sin{(2\pi en!)} =2\pi .$$

提示：利用习题$72$的公式$(\ast )$.

证$\quad $（本题也可放在$\S 1.2$中.）利用习题$72$中的结论，就有

$$\dfrac{1}{(n+1)!} < e-\left( 1+1+\dfrac{1}{2!} +\cdots +\dfrac{1}{n!} \right) < \dfrac{1}{n!n} .$$

将上式乘以$n!$后，中间是$n!e$减去一个正整数，而左边为$\dfrac{1}{n+1} $，右边为$\dfrac{1}{n} $，由此可见，中间就是$n!e-[n!e]$，即$n!e$的小数部分.再乘以$2\pi $就得到

$$\dfrac{2\pi }{n+1} < 2\pi (n!e -[n!e]) < \dfrac{2\pi }{n} .$$

当$n \geqslant 4$时利用$\sin{x}$在$[0,\dfrac{\pi }{2} ]$上单调递增，就有

$$\sin{\dfrac{2\pi }{n+1} } < \sin{(2\pi n!e)} < \sin{\dfrac{2\pi }{n} } .$$

最后两边乘以$n$并令$n\to \infty $就得到所求的极限为$2\pi $.

迭代生成的函数列

这是$\S 1.2$中有关迭代数列的习题$81$，$148-149$的继续.其中的规律性需要专门介绍.

先讲其中与众不同的一道题，所用的方法是柯西命题（即习题$138$）的进一步发展.

$637.3$.数列$y_n $借助于数列$x_n $由下述关系式定义：

$$y_0 =x_0 ,y_n =x_n -\alpha x_{n-1} (n=1,2,\cdots ),$$

其中$\vert \alpha \vert < 1$.若$\displaystyle \lim_{n\to \infty } y_n =b$，求$\displaystyle \lim_{n\to \infty } x_n $.

解$\quad $设$\alpha \neq 0$，否则不必再讨论.由于$\lbrace y_n \rbrace $的极限已知，我们可以用$\lbrace y_n \rbrace $去研究$\lbrace x_n \rbrace $.认为$\lbrace y_n \rbrace $已经给定，然后从$x_0 =y_0 $和

$$x_n =\alpha x_{n-1} +y_n (n=1,2,\cdots )$$

来确定数列$\lbrace x_n \rbrace $.用差分方程的语言来说，这就是一个一阶线性非齐次差分方程.（在$1.2.8$的习题$148$的解$3$中已经出现了线性差分方程.）另一方面也可以将上述方程看成为线性迭代，只是每次的$y_n $与$n$有关.

于是就有$x_0 =y_0 $，$x_1 =\alpha y_0 +y_1 $，$x_2 =\alpha^2 y_0 +\alpha y_1 +y_2 $，$\cdots $，一般地用数学归纳法可以证明有

$$x_n =\alpha^n y_0 +\alpha^{n-1} y_1 +\cdots +\alpha y_{n-1} +y_n .$$

为从此式证明$\lbrace x_n \rbrace $收敛，可以用柯西收敛准则（参见习题$81$的解$2$）.

下面将采取类似于$\S 1.2.4$的习题$81$的解$3$中的方法.首先，如果$\displaystyle \lim_{n\to \infty } x_n $存在的话，它等于什么？从$y_n =x_n -\alpha x_{n-1} $中令$n\to \infty $就得到

$$\lim_{n\to \infty } x_n =\dfrac{b}{1-\alpha } .$$

第二步，我们直接证明$\displaystyle \lim_{n\to \infty } \left( x_n -\dfrac{b}{1-\alpha } \right) =0$.由于

$$\begin{align}
& x_n -\dfrac{b}{1-\alpha } \\
= & x_n -b\left( 1+\alpha +\cdots +\alpha^n +\dfrac{\alpha^{n+1} }{1-\alpha } \right) \\
= & \alpha^n (y_0 -b)+\alpha^{n-1} (y_1 -b)+\cdots +\alpha (y_{n-1} -b)+(y_n -b)-\dfrac{b\alpha^{n+1} }{1-\alpha } ,
\end{align}$$

而$\vert \alpha \vert < 1$， 上式右边的最后一项极限为$0$，因此只要证明以下极限等式即可：

因此只要证明以下极限等式即可：

$$\lim_{n\to \infty } [\alpha^n (y_0 -b)+\alpha^{n-1} (y_1 -b)+\cdots +\alpha (y_{n-1} -b)+(y_n -b)]=0. \label{10} \tag{1.42} $$

下面的方法就是在$\S 1.2.7$中证明柯西命题（即习题$138$）的方法.

对于给定的任意$\varepsilon > 0$，存在$N_1 $，当$n > N_1 $时有$\vert y_n -b\vert < \varepsilon $.固定这个$N_1 $，将$\eqref{10}$左边的方括号内的表达式记为$\Delta_n $，然后进行分拆处理如下：

$$\begin{align}
& \vert \Delta_n \vert \\
= & \vert \alpha^n (y_0 -b)+\alpha^{n-1} (y_1 -b)+\cdots +\alpha (y_{n-1} -b)+(y_n -b)\vert \\
\leqslant & \vert \alpha^n (y_0 -b)+\alpha^{n-1} (y_1 -b)+\cdots +\alpha^{n-N_1 } (y_{N_1} -b)\vert \\
& +\vert \alpha^{n-N_1 -1} (y_{N_1 +1} -b)+\cdots +\alpha (y_{n-1} -b)+(y_n -b)\vert \\
\leqslant & \vert \alpha^n \vert \cdot \vert (y_0 -b)+\alpha^{-1} (y_1 -b)+\cdots +\alpha^{-N_1 } (y_{N_1 } -b)\vert \\
& +\varepsilon (1+\vert \alpha \vert +\cdots +\vert \alpha \vert^{n-N_1 -1} ).
\end{align}$$

由于$N_1 $已经固定，记$M=\vert (y_0 -b)+\alpha^{-1} (y_1 -b)+\cdots +\alpha^{-N_1 } (y_{N_1 } -b)\vert $，则就得到当$n > N_1 $时有

$$\vert \Delta_n \vert \leqslant M\cdot \vert \alpha \vert^n +\varepsilon \cdot \dfrac{1}{1-\vert \alpha \vert } .$$

由于$\vert \alpha \vert < 1$，存在$N > N_1 $，使得当$n > N$时$M\cdot \vert \alpha \vert^n < \varepsilon $.于是当$n > N$时就有

$$\vert \Delta_n \vert \leqslant \varepsilon \cdot \dfrac{2-\vert \alpha \vert }{1-\vert \alpha \vert } .$$

由于右边的$\varepsilon $的系数与$\varepsilon $和$n$无关，因此这就证明了$\displaystyle \lim_{n\to \infty } \Delta_n =0$.

下面我们指出，除了上一题和（习题$148$雷同的）习题$637.2$之外，其余的几个习题存在统一的规律和解法.（当然它不一定是对每个题的最佳解法.）

为简明起见，称$x_{n+1} =f(x_n ),n=1,2,\cdots $为迭代数列，称其中的函数$f$为迭代函数，以下均假设$f$与$n$无关.

首先有一个简单但很基本的如下规律.

命题$1.9\quad $设数列$\lbrace x_n \rbrace $满足迭代公式$x_{n+1} =f(x_n )$，$n=1,2,\cdots $，且已知有$\displaystyle \lim_{n\to \infty } x_n =\xi $，若又已知有

$$\lim_{n\to \infty } f(x_n ) =f(\xi ),$$

则极限$\xi $是方程$f(x)=x$的根（即$f$的不动点）.

注$\quad $条件$\displaystyle \lim_{n\to \infty } f(x_n ) =f(\xi )$在$f$于点$\xi $处连续时就成立.证明是直截了当的，但命题提供了一种方法，即在研究迭代数列时，经常先假设它收敛，看极限会是什么，然后再做下去.如前面的习题$637.3$的解法就是如此.该题中的迭代数列的迭代数与$n$有关，因此比上述命题中的问题要复杂一点.

值得指出，若迭代函数$f$没有不动点，则从命题$1.9$就推出数列$\lbrace x_n \rbrace $发散.

在迭代函数为单调时迭代数列的性态很简单，这就是下一个命题，它给出了迭代数列的单调性规律的理论依据.

命题$1.10\quad $设函数$f$在区间$I$上单调，数列$\lbrace x_n \rbrace $满足迭代公式$x_{n+1} =f(x_n ) $，$n=1,2,\cdots $，且$x_n \in I,n=1,2,\cdots $，则只有两种可能性：

$(a)$当$f$为单调递增时，$\lbrace x_n \rbrace $为单调数列；

$(b)$当$f$为单调递减时，$\lbrace x_n \rbrace $的子列$\lbrace x_{2n-1} \rbrace $和$\lbrace x_{2n} \rbrace $是具有相反单调性的两个单调子列.

这里我们只用图示来解释命题$1.10$的意义，其简单证明可以在$[23]$的$\S 2.6.2$中找到.附图中的分图$(a)$和$(b)$分别对应于命题$1.10$的情况$(a)$和情况$(b)$.分图$(c)$则表明命题$1.9$中的极限$\xi$不一定唯一.随着初始条件的不同，收敛的迭代数列可能有不同的极限.这只是对$f$单调递增作出的图.对$f$单调递减也有类似的结论.

下面用以上两个命题对$7$个习题作出统一的分析.我们的方法是先作出$f(x)$的草图，求出它与$y=x$的交点，即得出$f$的不动点.然后从$f$的图像的单调性来判断迭代数列的单调性.这就是将结果猜到之后（与命题无关地）再写出证明.

$606$.$\displaystyle \lim_{n\to \infty } \underbrace{\sin{\sin{} \cdots \sin{} }}_x{x} .$

分析$\quad $这个题与$\S 1.2.4$的习题$81$和下面的习题$637.1$等类似，可以改写为迭代数列来处理.定义$x_0 =x$，$x_n =\sin{x_{n-1} } (n=1,2,\cdots )$，于是迭代函数是$f(x)=\sin{x} $.无论$x_0 =x$如何，从$n=1$起总有$x_n \in [-1,1]$，而$f(x)=\sin{x} $在该区间上单调递增，因此可以从命题$1.10(a)$肯定$\lbrace x_n \rbrace $单调且有界，从而一定收敛.细节留给读者.

解$\quad $先设$0\leqslant x \leqslant \pi $，这时，$0\leqslant \sin{x} \leqslant x$，$0\leqslant \sin{(\sin{x} )} \leqslant \sin{x} $，依次类推.用数学归纳法，即可证得

$$0\leqslant \underbrace{\sin{\sin{} \cdots \sin{x} }}_{n次} \leqslant \underbrace{\sin{\sin{} \cdots \sin{x} }}_{n-1次} ,$$

这说明$\underbrace{\sin{\sin{} \cdots \sin{x} }}_{n次} $随着$n$的增大而单调减少，于是，由其有界性知极限

$$\displaystyle \lim_{n\to \infty } \underbrace{\sin{\sin{} \cdots \sin{x} }}_{n次} =\mu $$

存在有限，且$0\leqslant \mu \leqslant 1$，因此，

$$\lim_{n\to \infty } \underbrace{\sin{\sin{} \cdots \sin{x} }}_{n次} =\sin{} ( \lim_{n\to \infty } \underbrace{\sin{\sin{} \cdots \sin{x} }}_{n-1次} )$$

即$\sin{\mu } =\mu $，故$\mu =0$.

同法可证，当$\pi < x \leqslant 2\pi $时，

$$\displaystyle \lim_{n\to \infty } \underbrace{\sin{\sin{} \cdots \sin{x} }}_{n次} =0. $$

再利用$\sin{x}$的周期性（周期为$2\pi $），得知对任一$x$值，均有

$$\displaystyle \lim_{n\to \infty } \underbrace{\sin{\sin{} \cdots \sin{x} }}_{n次} =0. $$

$637.1$.数列$x_n $由等式

$$x_1 =\sqrt{a} ,x_2 =\sqrt{a+\sqrt{a} } ,x_3 =\sqrt{a+\sqrt{a+\sqrt{a} } } ,\cdots (a > 0) $$

给出，求$\displaystyle \lim_{n\to \infty } x_n $.

分析$\quad $如取$a=2$则就是前面的习题$81$，只是那里只要证明数列收敛.

这里的迭代函数是$f(x)=\sqrt{a+x} ,x\geqslant 0$.命题$1.9$可以用于事先确定极限值，命题$1.10$则可以确定数列$\lbrace x_n \rbrace $为单调递增.具体求解的写法可参考习题$81$的解$3$.

解$\quad $首先，我们注意到此数列显然是单调上升的.其次，由$x_n =\sqrt{a+x_{n-1}}$，得$x_n^2 =a+x_{n-1} $，即

$$x_n =\dfrac{a}{x_n } +\dfrac{x_{n-1} }{x_n } .\label{637.1.1} \tag{1}$$

因为$\sqrt{a} < x_{n-1} < x_n $，即在$\eqref{637.1.1}$式右端第二项小于$1$，所以

$$x_n < \dfrac{a}{x_n } +1.\label{637.1.2} \tag{2} $$

又显然有

$$x_n > \sqrt{a} (n=2,3,\cdots )\label{637.1.3} \tag{3} $$

将$\eqref{637.1.3}$式代入$\eqref{637.1.2}$式右端，即得$x_n < \sqrt{a} +1$，故数列$\lbrace x_n \rbrace $是有界的.

根据极限存在的准则可知，数列$\lbrace x_n \rbrace $的极限$\displaystyle \lim_{n\to \infty} x_n $存在，设其值为$l$.

利用等式$x_n^2 =a+x_{n-1} $，两端取极限，得$l^2=a+l$，解之，得

$$l=\dfrac{1\pm \sqrt{1+4a} }{2} (a > 0),$$

负根不适合（因为$x_n > 0$），只取其正根，即$\displaystyle \lim_{n\to \infty } x_n =\dfrac{1+ \sqrt{1+4a} }{2}$.

$637.2$.数列$x_n $按下述方式给出：

$$x_1 =0,x_2 =1,x_n =\dfrac{1}{2} (x_{n-1} +x_{n-2} )(n=3,4,\cdots ).$$

求$\displaystyle \lim_{n\to \infty } x_n $.

解$\quad $由于

$$x_{n+1} -x_n =\dfrac{x_n +x_{n-1}}{2} -x_n =\dfrac{x_{n-1} -x_n }{2} =\cdots =\dfrac{x_2 -x_1 }{(-2)^{n-1}} =\dfrac{1}{(-2)^{n-1}} $$

及

$$x_{n+1} =\sum_{m=1}^n (x_{m+1} -x_m )+x_1 =\sum_{m=1}^n \dfrac{1}{(-2)^{m-1}} ,$$

所以，$\displaystyle \lim_{n\to \infty } x_n =\dfrac{1}{1-\left( -\dfrac{1}{2} \right) } =\dfrac{2}{3} $.

$637.4$.数列$x_n $由下述方式给出：

$$x_0 =1,x_n =\dfrac{1}{1+x_{n-1} } (n=1,2,\cdots ).$$

求$\displaystyle \lim_{n\to \infty } x_n $.

提示：考虑$x_n $与方程$x=\dfrac{1}{1+x} $的根之差.

分析$\quad $由于数列每项大于$0$，因此迭代函数为$f(x)=\dfrac{1}{1+x} (x > 0)$.由$x=f(x)$求出不动点，记为$\xi =\dfrac{1}{2} (-1+\sqrt{5} )(\approx 0.618)$.从命题$1.10$知道本题属于情况$(b)$（参看附图$(b)$），即需证$\lbrace x_n \rbrace $的奇数项子列和偶数项子列分别单调，且收敛于同一极限$\xi $.

但本题可以如前面的习题$637.3$那样，在求出$\xi $之后直接证明$\displaystyle \lim_{n\to \infty } (x_n -\xi )=0$.这是因为下面的估计比较容易：

$$\begin{align}
& \vert x_n -\xi \vert \\
= & \left\vert \dfrac{1}{1+x_{n-1} } -\dfrac{1}{1+\xi } \right\vert \\
= & \dfrac{\vert x_{n-1} -\xi \vert }{(1+x_{n-1} )(1+\xi )} \\
\leqslant & \dfrac{1}{1+\xi } \cdot \vert x_{n-1} -\xi \vert .
\end{align}$$

$638$.函数序列

$$y_n =y_n (x) (0\leqslant x\leqslant 1)$$

用以下方式确定：

$(a)y_1 =\dfrac{x}{2} ,y_n =\dfrac{x}{2} -\dfrac{y_{n-1}^2 }{2} (n=2,3,\cdots )$；

$(b)y_1 =\dfrac{x}{2} ,y_n =\dfrac{x}{2} +\dfrac{y_{n-1}^2 }{2} (n=2,3,\cdots )$.

解$(a)$分析$\quad $本题中的自变量$x$只不过是一个参数，因此前面的两个命题和方法都适用.这时的迭代函数是$f(y)=\dfrac{x}{2} -\dfrac{y^2}{2} $.

由初值$y_1 =\dfrac{x}{2} $和参数范围$0\leqslant x \leqslant 1$可以确定$y_n (x) \in [0,\dfrac{x}{2} ]$始终成立，而在此区间上迭代函数$f$单调递减，因此属于命题$1.10$的情况$(b)$.但是这里用上一题的方法更容易一些.这就是从$y=f(y)$直接解出$y(x)=-1+\sqrt{1+x} $.然后证明对于$0 \leqslant x\leqslant 1$上的每个$x$都有$\displaystyle \lim_{n\to \infty } (y_n (x)-y(x))=0$.以下请读者写出细节.

解$\quad $当$x=0$时，$y_n =0,n=1,2,\cdots $，则$\displaystyle \lim_{n\to \infty } y_n =0$.

当$0 < x\leqslant 1$时，用数学归纳法可证$y_n > 0$，$n=1,2,\cdots \colon y_1 > 0$.若$y_k > 0$，由$x > y_{k-1}^2$，可得

$$y_{k+1} =\dfrac{x}{2} -\dfrac{y_k^2}{2} =\dfrac{4x-(x-y_{k-1}^2)^2}{8} \geqslant \dfrac{3x}{8} > 0.$$

因而有

$$y_1 -y_3 =\dfrac{y_2^2}{2} > 0,y_2 -y_4 =\dfrac{y_3^2 -y_1^2}{2} < 0,\cdots $$

用数学归纳法可证

$$y_{2n} -y_{2n+2} < 0,y_{2n-1} -y_{2n+1} > 0 (n=1,2,\cdots ).$$

即

$$\dfrac{x}{2} =y_1 > y_3 > \cdots > 0,0 < y_2 < y_4 < \cdots < \dfrac{x}{2} .$$

可见序列$y_1 ,y_3 ,\cdots $及序列$y_2 ,y_4 ,\cdots $都是收敛的.设极限分别为$A_1 ,A_2 $，由

$$y_{2n} =\dfrac{x}{2} -\dfrac{y_{2n-1}^2}{2} ,y_{2n+1} =\dfrac{x}{2} -\dfrac{y_{2n}^2}{2} ,$$

求极限得$A_2 =\dfrac{x}{2} -\dfrac{A_1^2}{2} ,A_1 =\dfrac{x}{2} -\dfrac{A_2^2}{2} $，相减得$A_1 -A_2 =(A_1 -A_2 )\dfrac{(A_1 +A_2 )}{2} $.而$0\leqslant A_1 \leqslant \dfrac{x}{2} \leqslant \dfrac{1}{2} $，$0\leqslant A_2 \leqslant \dfrac{x}{2} \leqslant \dfrac{1}{2} $，故

$$A_1 =A_2 =A.$$

用极限定义直接可以证明：若$\lbrace y_n \rbrace $的两个子序列$\lbrace y_{2n} \rbrace $及$\lbrace y_{2n-1} \rbrace (n=1,2,\cdots )$收敛于同一个极限，则$\lbrace y_n \rbrace $也收敛地这个极限，由$A=\dfrac{x}{2} -\dfrac{A^2}{2} $解得$A=\sqrt{1+x} -1$，即$\displaystyle \lim_{n\to \infty } y_n =\sqrt{1+x} -1$.

$(b)$分析$\quad $此题中迭代函数$f(y)=\dfrac{x}{2} +\dfrac{y^2}{2} $为单调递增函数，属于命题$1.10$的情况$(a)$，因此只要证明对每个$x\in [0,1]$的$\lbrace y_n \rbrace $关于$n$为单调有界就解决了收敛性问题，再从命题$1.9$得到极限函数为$y(x)=1+\sqrt{1-x} $.当然用上一题的方法也可以成功.

解$\quad $显然，$y_2 > y_1 $.假设$y_n \geqslant y_{n-1} $，则由$y_{n+1} -y_n =\dfrac{y_n^2 -y_{n-1}^2 }{2} $可推出$y_{n+1} \geqslant y_n $.

由数学归纳法得知，序列$\lbrace y_n \rbrace $单调上升.

现在我们证明这个序列有界.显然，

$$0\leqslant y_1 < 1.$$

设$0\leqslant y_k < 1$，则$0\leqslant y_k^2 < 1$，且$0\leqslant y_{k+1} < 1 $.由数学归纳法便得知序列$\lbrace y_n \rbrace $有界.

这样，我们就证明了此序列的极限$\displaystyle \lim_{n\to \infty } y_n $存在.设其值为$l$（显然$0\leqslant l\leqslant 1$），即得$l=\dfrac{x}{2} +\dfrac{l^2}{2} $，解之，得$l=1\pm \sqrt{1-x} $.由于$0\leqslant l\leqslant 1$，故必

$$\lim_{n\to \infty } y_n =l=1-\sqrt{1+x} .$$

$639.1$.设$x > 0$且$y_n =y_{n-1} (2-xy_{n-1} )(n=1,2,\cdots )$.证明：若$y_i > 0(i=0,1)$，则序列$y_n $收敛且

$$\displaystyle \lim_{n\to \infty } y_n =\dfrac{1}{x} .$$

提示：研究差$\dfrac{1}{x} -y_n $.

分析$\quad $这里$x$同样只起着正参数的作用.迭代函数为$f(y)=y(2-xy)$.它的不动点就是$\dfrac{1}{x} $.如附图所示，这个不动点恰好也是迭代函数$f$的极大值点.

于是从条件$y_1 > 0$可推出只能取$y_0 \in (0,\dfrac{2}{x} )$.若$y_0 =\dfrac{1}{x} $，则当然就“不动”了.若$0 < y_0 < \dfrac{1}{x} $，则就是命题$1.10$的情况$(a)$.最后，若$\dfrac{1}{x} < y_0 < \dfrac{2}{x} $，则$y_1 \in (0,\dfrac{1}{x} )$，因此与上面的情况相同.

$639.2$.为了求$y=\sqrt{x} $，其中$x > 0$，采用如下步骤：$y_0 > 0$是任意的，

$$y_n =\dfrac{1}{2} \left( y_{n-1} +\dfrac{x}{y_{n-1} } \right) (n=1,2,\cdots ).$$

证明：$\displaystyle \lim_{n\to \infty } y_n =\sqrt{x} $.

提示：利用公式

$$\dfrac{y_n -\sqrt{x} }{y_n +\sqrt{x} } =\left( \dfrac{y_{n-1} -\sqrt{x} }{y_{n-1} +\sqrt{x} } \right)^2 (n\geqslant 1).$$

分析$\quad $若取$x=1$则就是习题$149$.请参看$\S 1.2.8$中该题的解法以及后面的两个注.注意本题中的不动点也恰好是迭代函数的极值点，因此与上一题有类似的分析.

与上述$7$个题不同，在下面一题中起主要作用的是关于正弦函数$\sin{x}$的不等式$0 < \vert \sin{x} \vert < \vert x\vert (x\neq 0)$.

$640$.为了求开普勒方程

$$x-\varepsilon \sin{x} =m(0 < \varepsilon < 1)\label{640} \tag{1} $$

的近似解，假设

$$x_0 =m,x_1 =m+\varepsilon \sin{x_0 } ,\cdots ,x_n =m+\varepsilon \sin{x_{n-1} } ,\cdots $$

（逐步逼近法）.证明：存在$\xi =\displaystyle \lim_{n\to \infty } x_n $，且数$\xi $为方程$\eqref{640} $的唯一的根.

证$\quad $这里的迭代函数为$f(x)=m+\varepsilon \sin{x} $，一次迭代之后就只需要在$[m-\varepsilon ,m+\varepsilon ]$上研究$f$了，但其单调性分析不是非常方便.因此下面改用其他方法来做.

首先看方程解的唯一性.若有$x_1 ,x_2 $都满足方程$x-\varepsilon \sin{x} =m$，则将$x_1 ,x_2 $分别代入，然后将两式相减就得到

$$\begin{align}
& \vert x_1 -x_2 \vert \\
= & \varepsilon \cdot \vert \sin{x_1 } -\sin{x_2} \vert \\
= & \varepsilon \cdot \left\vert 2\sin{\dfrac{x_1 -x_2 }{2} } \cos{\dfrac{x_1 +x_2 }{2} }\right\vert \\
\leqslant & \varepsilon \cdot \vert x_1 -x_2 \vert ,
\end{align}$$

由条件$\varepsilon \in (0,1)$可见只能有$x_1 =x_2 $.

用相同的方法可以导出最近两次迭代之差满足以下不等式：

$$\vert x_{n+1} -x_n \vert \leqslant \varepsilon \vert x_n -x_{n-1} \vert (n=1,2,\cdots ),$$

于是就可以用柯西收敛准则来证明数列$\lbrace x_n \rbrace $收敛（参见$\S 1.2.5$的习题$82$等）.具体来说，对于任何正整数$p$有

$$\vert x_{n+p} -x_n \vert \leqslant \varepsilon \vert x_{n+p-1} -x_{n-1} \vert \leqslant \cdots \leqslant \varepsilon^n \vert x_p -x_0 \vert \leqslant \varepsilon^{n+1} .$$

其中最后一步利用了$x_0 =m$和$\vert x_p -m \vert =\vert \varepsilon\sin{x_{p-1}} \vert \leqslant \varepsilon $.

由于$0 < \varepsilon < 1$保证了$\varepsilon^n \to 0$，因此对于任意的$\delta > 0$，存在$N$，当$n > N$时，对任意的正整数$p$，都成立$\vert x_{n+p} -x_{n} \vert < \delta $，于是从柯西准则知道迭代数列$\lbrace x_n \rbrace $收敛.

注$\quad $以上方法就是压缩映射原理，可参见$[23]$的$\S 3.4.4$中的介绍.

这里要指出，命题$1.10$中总结的迭代数列的单调性规律只是迭代数列理论中最为初等的部分.其中的主要条件是该数列落在迭代函数的某个单调区间内.如果该条件不成立，则情况完全不同.这时的迭代数列会有极其复杂的性态，它就是二十世纪七直年代出现的新科学——混沌学——的源头之一.对此有兴趣的读者可以阅读$[23]$中的$\S 5.6$，也可以直接阅读这方面的科普读物$[8]$和入门读物$[9]$.

为了让有兴趣的读者能够产生在这方面的一点感觉，不妨举一个在混沌学中最简单的例子，看其中会发生些什么，而将它们的证明略去.

如右图所示，取迭代函数$y=f(x)=4x(1-x),0\leqslant x\leqslant 1$.

初看起来这个迭代函数只不过是开口向下的一条抛物线.它只有两个单调区间：$[0,0.5]$和$[0.5,1]$.这样的情况在前面的习题$639.1$（参见其附图）和其他习题中都出现过，似乎是平淡无奇的.

然而这里的迭代数列则完全不同.若取初值$x_0 \in [0,1]$，然后用$x_n =f(x_{n-1} )$，$n=1,2,\cdots $，生成迭代数列，则除了$x_0 =0$和$x_0 =0.75$（即图中由$y=f(x)$和$y=x$的交点所确定的两个不动点）之外，其他迭代数列不可能完全落在$f$的某个单调区间内.

下面列出由这个迭代函数生成的迭代数列会具有的一些性态：

$(1)$存在周期为$3$的迭代数列.这在图上已经画出，即从$x_0 =\sin{}^2 20^{\circ} \approx 0.0117$出发，就可以计算得出$x_1 =\sin{}^2 40^{\circ} $，$x_2 =\sin{}^2 80^{\circ} $，$x_3 =x_0 $，于是以后就以周期$3$重复了.这当然是发散数列，并有三个聚点.

$(2)$引用著名论文中的第一定理，就知道只要选取适当的初值，就可以生成最小周期等于每一个正整数$n$的周期迭代数列.（不动点就是周期$1$的迭代数列.）

$(3)$再引用同一论文的第二定理，就知道存在一个不可列数集$S\subset [0,1]$.在$S$中任何两个不相等的初值$x_0 \neq y_0 $所生成的迭代数列$\lbrace x_n \rbrace $和$\lbrace y_n \rbrace $之间都具有以下性质：

$$\varliminf_{n\to \infty } \vert y_n -x_n \vert =0,\varlimsup_{n\to \infty } \vert y_n -x_n \vert > 0,$$

也就是说它们既会无限接近，又总是会分开.这样的性态可称复杂了.在混沌学中的第一个可操作的混沌定义即是以此为主要依据而产生的.

$(4)$只要在取初值$x_0 $时避开$[0,1]$中的一个可列集（包括$0,0.75$等），则所生成的每一个数列$\lbrace x_n \rbrace $就会在区间$[0,1]$内处处稠密，于是其聚点全体就是区间$[0,1]$.这种“遍历性”是与收敛性截然相反的性态.

最后应当指出，就迭代函数为$f(x)=4x(1-x)$来说，对以上各点作出严格证明还是比较容易的，然而如果讨论更为一般的抛物线映射

$$f(x)=bx(1-x),0 \leqslant x\leqslant 1,0 < b\leqslant 4,$$

即带有参数$b\in (0,4]$时，同j问题就要复杂得多.对于它的研究已经包含着离散动力系统的许多基本内容.这也就是参考文献《从抛物线谈起》的书名的由来.